Раздел (теория чисел)

Разложение целого числа в сумму натуральных чисел

Диаграммы Юнга соответствуют разбиениям натуральных чисел от 1 до 8. Они устроены так, что изображения при отражении относительно главной диагонали квадрата являются сопряженными разбиениями.

Разделы n с наибольшей частью k

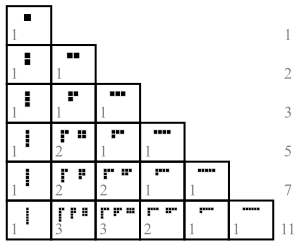
В теории чисел и комбинаторике разбиение неотрицательного целого числа n , также называемое целочисленным разбиением , представляет собой способ записи n в виде суммы положительных целых чисел . Две суммы, отличающиеся только порядком слагаемых, считаются одним и тем же разбиением. (Если порядок имеет значение, сумма становится композицией .) Например, число 4 можно разделить пятью различными способами:

4

3 + 1

2 + 2

2 + 1 + 1

1 + 1 + 1 + 1

Единственное разбиение нуля — это пустая сумма, не имеющая частей.

Зависимая от порядка композиция 1 + 3 — это тот же раздел, что и 3 + 1 , а две отдельные композиции 1 + 2 + 1 и 1 + 1 + 2 представляют тот же раздел, что и 2 + 1 + 1 .

Отдельное слагаемое в разделе называется частью . Количество разделов n определяется статистической суммой p ( n ) . Итак, р (4) = 5 . Обозначение λ ⊢ n означает, что λ является разбиением n .

Разделы можно графически визуализировать с помощью диаграмм Юнга или диаграмм Феррера . Они встречаются в ряде разделов математики и физики , включая изучение симметричных многочленов и симметрической группы , а также в теории представлений групп в целом.

Примеры

Семь разделов из 5

• 5
• 4 + 1
• 3 + 2
• 3 + 1 + 1
• 2 + 2 + 1
• 2 + 1 + 1 + 1
• 1 + 1 + 1 + 1 + 1

Некоторые авторы рассматривают разбиение как убывающую последовательность слагаемых, а не как выражение со знаком плюс. Например, раздел 2 + 2 + 1 вместо этого можно записать в виде кортежа (2, 2, 1) или в еще более компактной форме (2 ² , 1) , где верхний индекс указывает количество повторений части.

Это обозначение кратности для раздела можно альтернативно записать как , где m ₁ — количество единиц, m ₂ — количество двоек и т. д. (Компоненты с m _i = 0 могут быть опущены.) Например, в этом обозначении разбиения 5 записаны , и . ${\displaystyle 1^{m_{1}}2^{m_{2}}3^{m_{3}}\cdots }$ ${\displaystyle 5^{1},1^{1}4^{1},2^{1}3^{1},1^{2}3^{1},1^{1}2^{2},1^{3}2^{1}}$ ${\displaystyle 1^{5}}$

Схематические изображения перегородок

Существует два распространенных схематических метода представления разделов: диаграммы Феррера, названные в честь Нормана Маклеода Феррерса , и диаграммы Янга, названные в честь Альфреда Янга . Оба имеют несколько возможных соглашений; здесь мы используем английскую систему обозначений , при этом диаграммы выравниваются по левому верхнему углу.

Диаграмма Феррера

Раздел 6+4+3+1 числа 14 можно представить следующей схемой:

14 кругов выстроены в 4 ряда, каждый размером с часть перегородки. Схемы 5-ти перегородок номера 4 показаны ниже:

Диаграмма Янга

Альтернативным визуальным представлением целочисленного раздела является его диаграмма Юнга (часто также называемая диаграммой Феррера). Вместо представления разделения точками, как на диаграмме Феррера, на диаграмме Янга используются прямоугольники или квадраты. Таким образом, диаграмма Юнга для разбиения 5 + 4 + 1 имеет вид

в то время как диаграмма Феррера для того же раздела имеет вид

Хотя этот, казалось бы, тривиальный вариант не кажется заслуживающим отдельного упоминания, диаграммы Юнга оказываются чрезвычайно полезными при изучении симметричных функций и теории представления групп : заполнение ячеек диаграмм Юнга числами (или иногда более сложными объектами), подчиняющимися различным правилам. приводит к семейству объектов, называемых таблицами Юнга , и эти таблицы имеют комбинаторное и теоретико-представление значение. ^[1] Как тип фигуры, состоящей из соединенных вместе соседних квадратов, диаграммы Юнга представляют собой особый вид полимино . ^[2]

Функция разделения

Использование метода Эйлера для нахождения p (40): линейка со знаками плюс и минус (серый прямоугольник) перемещается вниз, соответствующие части добавляются или вычитаются. Положения знаков задаются разностью чередующихся натуральных (синих) и нечетных (оранжевых) чисел. В файле SVG наведите указатель мыши на изображение, чтобы переместить линейку.

Функция секционирования подсчитывает части неотрицательного целого числа . Например, поскольку целое число имеет пять разделов , , , и . Значения этой функции для : ${\displaystyle p(n)}$ ${\displaystyle n}$ ${\displaystyle p(4)=5}$ ${\displaystyle 4}$ ${\displaystyle 1+1+1+1}$ ${\displaystyle 1+1+2}$ ${\displaystyle 1+3}$ ${\displaystyle 2+2}$ ${\displaystyle 4}$ ${\displaystyle n=0,1,2,\dots }$

1, 1, 2, 3, 5, 7, 11, 15, 22, 30, 42, 56, 77, 101, 135, 176, 231, 297, 385, 490, 627, 792, 1002, 1255, 1575, 1958, 2436, 3010, 3718, 4565, 5604, ... (последовательность A000041 в OEIS ).

Производящая функция _ _ ${\displaystyle p}$

${\displaystyle \sum _{n=0}^{\infty }p(n)q^{n}=\prod _{j=1}^{\infty }\sum _{i=0}^{\infty }q^{ji}=\prod _{j=1}^{\infty }(1-q^{j})^{-1}.}$

Выражение в замкнутой форме для статистической суммы неизвестно, но оно имеет как асимптотические разложения , которые точно аппроксимируют ее, так и рекуррентные соотношения , с помощью которых ее можно точно вычислить. Он растет как экспоненциальная функция квадратного корня из своего аргумента. ^[3] следующим образом:

${\displaystyle p(n)\sim {\frac {1}{4n{\sqrt {3}}}}\exp \left({\pi {\sqrt {\frac {2n}{3}}}}\right)}$как ${\displaystyle n\to \infty }$

В 1937 году Ганс Радемахер нашел способ представить статистическую сумму сходящимся рядом . ${\displaystyle p(n)}$

$${\displaystyle p(n)={\frac {1}{\pi {\sqrt {2}}}}\sum _{k=1}^{\infty }A_{k}(n){\sqrt {k}}\cdot {\frac {d}{dn}}\left({{\frac {1}{\sqrt {n-{\frac {1}{24}}}}}\sinh \left[{{\frac {\pi }{k}}{\sqrt {{\frac {2}{3}}\left(n-{\frac {1}{24}}\right)}}}\,\,\,\right]}\right)}$$

$${\displaystyle A_{k}(n)=\sum _{0\leq m<k,\;(m,k)=1}e^{\pi i\left(s(m,k)-2nm/k\right)}.}$$

сумму Дедекинда ${\displaystyle s(m,k)}$

Мультипликативная обратная производящая функция — это функция Эйлера ; по теореме Эйлера о пятиугольных числах эта функция представляет собой знакопеременную сумму степеней пятиугольных чисел своего аргумента.

${\displaystyle p(n)=p(n-1)+p(n-2)-p(n-5)-p(n-7)+\cdots }$

Шриниваса Рамануджан обнаружил, что статистическая сумма имеет нетривиальные закономерности в модульной арифметике , известные теперь как сравнения Рамануджана . Например, всякий раз, когда десятичное представление числа заканчивается цифрой 4 или 9, количество разделов будет делиться на 5. ^[4] ${\displaystyle n}$ ${\displaystyle n}$

Ограниченные разделы

И в комбинаторике, и в теории чисел часто изучаются семейства разбиений, на которые распространяются различные ограничения. ^[5] В этом разделе рассматриваются некоторые такие ограничения.

Сопряженные и самосопряженные перегородки

Если перевернуть схему разбиения 6 + 4 + 3 + 1 вдоль его главной диагонали, то получим еще одно разбиение из 14:

Превратив строки в столбцы, получим разбиение 4 + 3 + 3 + 2 + 1 + 1 числа 14. Такие разбиения называются сопряженными друг другу. ^[6] В случае числа 4 разбиения 4 и 1 + 1 + 1 + 1 являются сопряженными парами, а разбиения 3 + 1 и 2 + 1 + 1 сопряжены друг с другом. Особый интерес представляют разбиения, например 2+2, которые сами по себе являются сопряженными. Такие разбиения называются самосопряженными . ^[7]

Утверждение : количество самосопряженных разделов равно количеству разделов с различными нечетными частями.

Доказательство (схема) . Важнейшее наблюдение состоит в том, что каждую нечетную часть можно « сложить » посередине, чтобы сформировать самосопряженную диаграмму:

Затем можно получить биекцию между набором разбиений с различными нечетными частями и набором самосопряженных разбиений, как иллюстрируется следующим примером:

Нечетные части и отдельные части

Среди 22 разделов числа 8 есть 6, которые содержат только нечетные части :

• 7 + 1
• 5 + 3
• 5 + 1 + 1 + 1
• 3 + 3 + 1 + 1
• 3 + 1 + 1 + 1 + 1 + 1
• 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1

В качестве альтернативы мы могли бы подсчитать разделы, в которых ни одно число не встречается более одного раза. Такой раздел называется разделом, состоящим из отдельных частей . Если посчитать разбиения 8 на отдельные части, то тоже получим 6:

• 8
• 7 + 1
• 6 + 2
• 5 + 3
• 5 + 2 + 1
• 4 + 3 + 1

Это общее свойство. Для каждого положительного числа количество разделов с нечетными частями равно количеству разделов с различными частями, обозначаемому q ( n ). ^{[8] [9]} Этот результат был доказан Леонардом Эйлером в 1748 году ^[10] и позже был обобщен как теорема Глейшера .

Для каждого типа ограниченного раздела существует соответствующая функция количества разделов, удовлетворяющих данному ограничению. Важным примером является q ( n ) (разделение на отдельные части). Первые несколько значений q ( n ) (начиная с q (0)=1):

1, 1, 1, 2, 2, 3, 4, 5, 6, 8, 10, ... (последовательность A000009 в OEIS ).

Производящая функция для q ( n ) определяется выражением ^[11]

${\displaystyle \sum _{n=0}^{\infty }q(n)x^{n}=\prod _{k=1}^{\infty }(1+x^{k})=\prod _{k=1}^{\infty }{\frac {1}{1-x^{2k-1}}}.}$

Теорема о пятиугольных числах дает возврат для q : ^[12]

q ( ​​k ) знак равно a _k + q ( k - 1) + q ( k - 2) - q ( k - 5) - q ( k - 7) + q ( k - 12) + q ( k - 15) - q ( ​​k − 22) − ...

где a _k равно (−1) ^m , если k = 3 m ² − m для некоторого целого числа m , и равно 0 в противном случае.

Ограниченный размер или количество деталей.

Если взять сопряженные числа, то число p _k ( n ) разбиений числа n ровно на k частей будет равно количеству разбиений числа n , в которых наибольшая часть имеет размер k . Функция p _k ( n ) удовлетворяет рекуррентному правилу

п _k ( п ) знак равно п _k ( п - k ) + п _{k -1} ( п - 1)

с начальными значениями p ₀ (0) = 1 и p _k ( n ) = 0 , если n ≤ 0 или k ≤ 0 и n и k не равны нулю. ^[13]

Функцию p ( n ) можно восстановить с помощью

${\displaystyle p(n)=\sum _{k=0}^{n}p_{k}(n).}$

Одна из возможных производящих функций для таких разделов с фиксированным k и переменным n :

${\displaystyle \sum _{n\geq 0}p_{k}(n)x^{n}=x^{k}\prod _{i=1}^{k}{\frac {1}{1-x^{i}}}.}$

В более общем смысле, если T — набор положительных целых чисел, то количество разделов n , все части которых принадлежат T , имеет производящую функцию

${\displaystyle \prod _{t\in T}(1-x^{t})^{-1}.}$

Это можно использовать для решения проблем с внесением сдачи (где набор T указывает доступные монеты). В качестве двух частных случаев можно отметить, что количество разбиений n , в которых все части равны 1 или 2 (или, что то же самое, количество разбиений n на 1 или 2 части), равно

${\displaystyle \left\lfloor {\frac {n}{2}}+1\right\rfloor ,}$

а количество разбиений n , в которых все части равны 1, 2 или 3 (или, что то же самое, количество разбиений n не более чем на три части), является ближайшим целым числом к ​​( n + 3) ^{2/12 . [} 14 ^]

Разбиения в прямоугольнике и биномиальные коэффициенты Гаусса

Также можно одновременно ограничить количество и размер деталей. Пусть p ( N , M ; n ) обозначает количество разбиений n не более чем на M частей, каждая из которых имеет размер не более N . Эквивалентно, это разбиения, диаграмма Юнга которых помещается внутри прямоугольника M × N. Существует рекуррентное соотношение

$${\displaystyle p(N,M;n)=p(N,M-1;n)+p(N-1,M;n-M)}$$

nMNn - MM^[15] ${\displaystyle p(N,M;n)-p(N,M-1;n)}$

Биномиальный коэффициент Гаусса определяется как:

$${\displaystyle {k+\ell \choose \ell }_{q}={k+\ell \choose k}_{q}={\frac {\prod _{j=1}^{k+\ell }(1-q^{j})}{\prod _{j=1}^{k}(1-q^{j})\prod _{j=1}^{\ell }(1-q^{j})}}.}$$

производящейp ( N , M ; n )

$${\displaystyle \sum _{n=0}^{MN}p(N,M;n)q^{n}={M+N \choose M}_{q}.}$$

Площадь Ранка и Дёрфи

Ранг раздела — это наибольшее число k такое , что раздел содержит не менее k частей размером не менее k . Например, разбиение 4 + 3 + 3 + 2 + 1 + 1 имеет ранг 3, поскольку оно содержит 3 части с числом ≥ 3, но не содержит 4 частей с числом ≥ 4. В диаграмме Феррера или диаграмме Юнга разбиения ранга r , квадрат r × r записей в левом верхнем углу известен как квадрат Дерфи :

Квадрат Дёрфи находит применение в комбинаторике для доказательства различных тождеств разбиения. ^[16] Он также имеет некоторое практическое значение в виде индекса Хирша .

Другая статистика также иногда называется рангом раздела (или рангом Дайсона), а именно, разницей для раздела из k частей с наибольшей частью . Эта статистика (не имеющая отношения к описанной выше) появляется при изучении сравнений Рамануджана . ${\displaystyle \lambda _{k}-k}$ ${\displaystyle \lambda _{k}}$

Решетка Юнга

На разбиениях существует естественный частичный порядок , задаваемый включением диаграмм Юнга. Этот частично упорядоченный набор известен как решетка Юнга . Решетка была первоначально определена в контексте теории представлений , где она используется для описания неприводимых представлений симметрических групп Sn для всех n вместе с их свойствами ветвления _в нулевой характеристике. Его чисто комбинаторные свойства также подверглись серьезному изучению; в частности, это мотивирующий пример дифференциального ЧУУ .

Смотрите также

• Ранг раздела , другое понятие ранга
• Рукоятка перегородки
• Порядок доминирования
• Факторизация
• Целочисленная факторизация
• Раздел набора
• Звезды и полосы (комбинаторика)
• Плоская перегородка
• Вежливое число , определяемое делением на последовательные целые числа.
• Мультипликативный раздел
• Двенадцатикратный путь
• Формула выборки Юэнса
• Формула Фаа ди Бруно
• Многораздельность
• Личности Ньютона
• Функция наименьших деталей
• Разделение Гольдбаха — это разбиение четного числа на простые числа (см. гипотезу Гольдбаха ).
• Статистическая сумма Костанта

Примечания

1. Эндрюс 1976, с. 199.
2. Жосуа-Верже, Матье (2010), «Биекции между заполнениями диаграмм Юнга, избегающими шаблонов», Журнал комбинаторной теории , серия A, 117 (8): 1218–1230, arXiv : 0801.4928 , doi : 10.1016/j.jcta .2010.03.006, МР  2677686, S2CID  15392503.
3. Эндрюс 1976, с. 69.
4. Харди и Райт 2008, с. 380.
5. Олдер, Генри Л. (1969). «Тождества разбиений - от Эйлера до современности». Американский математический ежемесячник . 76 (7): 733–746. дои : 10.2307/2317861. JSTOR  2317861.
6. Харди и Райт 2008, с. 362.
7. Харди и Райт 2008, с. 368.
8. Харди и Райт 2008, с. 365.
9. Обозначения следуют Abramowitz & Stegun 1964, p. 825
10. Эндрюс, Джордж Э. (1971). Теория чисел . Филадельфия: Компания WB Saunders. стр. 149–50.
11. Абрамовиц и Стегун 1964, с. 825, 24.2.2 экв. Я (Б)
12. Абрамовиц и Стегун 1964, с. 826, 24.2.2 экв. II(А)
13. Ричард Стэнли, Перечислительная комбинаторика , том 1, второе издание. Издательство Кембриджского университета, 2012. Глава 1, раздел 1.7.
14. Харди, GH (1920). Некоторые известные проблемы теории чисел. Кларендон Пресс.
15. Эндрюс 1976, стр. 33–34.
16. см., например, Stanley 1999, p. 58

Рекомендации

• Абрамовиц, Милтон ; Стегун, Ирен (1964). Справочник по математическим функциям с формулами, графиками и математическими таблицами . Министерство торговли США, Национальное бюро стандартов. ISBN 0-486-61272-4.
• Эндрюс, Джордж Э. (1976). Теория перегородок . Издательство Кембриджского университета. ISBN 0-521-63766-Х.
• Эндрюс, Джордж Э.; Эрикссон, Киммо (2004). Целочисленные разделы . Издательство Кембриджского университета. ISBN 0-521-60090-1.
• Апостол, Том М. (1990) [1976]. Модульные функции и ряды Дирихле в теории чисел . Тексты для аспирантов по математике . Том. 41 (2-е изд.). Нью-Йорк и др.: Springer-Verlag . ISBN 0-387-97127-0. Збл  0697.10023. (См. главу 5, где представлено современное педагогическое введение в формулу Радемахера) .
• Бона, Миклош (2002). Прогулка по комбинаторике: введение в перечисление и теорию графов . Мировое научное издательство. ISBN 981-02-4900-4.(элементарное введение в тему целочисленных разделов, включая обсуждение графов Феррера)
• Харди, штат Джорджия ; Райт, Э.М. (2008) [1938]. Введение в теорию чисел . Под редакцией Д. Р. Хита-Брауна и Дж. Х. Сильвермана . Предисловие Эндрю Уайлса . (6-е изд.). Оксфорд: Издательство Оксфордского университета . ISBN 978-0-19-921986-5. МР  2445243. Збл  1159.11001.
• Лемер, Д.Х. (1939). «Об остатке и сходимости ряда для статистической суммы». Пер. амер. Математика. Соц . 46 : 362–373. дои : 10.1090/S0002-9947-1939-0000410-9 . МР  0000410. Збл  0022.20401.Предоставляет основную формулу (без производных), остаток и старую форму для A _k ( n ).)
• Гупта, Хансрадж; Гвитер, CE; Миллер, JCP (1962). Королевское математическое общество. Таблицы . Том. 4. Таблицы разделов. (Есть текст, почти полная библиография, но они (и Абрамовиц) пропустили формулу Сельберга для A _k ( n ), которая есть у Уайтмена.)
• Макдональд, Ян Г. (1979). Симметричные функции и полиномы Холла . Оксфордские математические монографии. Издательство Оксфордского университета . ISBN 0-19-853530-9. Збл  0487.20007.(См. раздел I.1)
• Натансон, МБ (2000). Элементарные методы теории чисел . Тексты для аспирантов по математике. Том. 195. Шпрингер-Верлаг . ISBN 0-387-98912-9. Збл  0953.11002.
• Радемахер, Ганс (1974). Сборник статей Ганса Радемахера . Том. v II. МТИ Пресс. стр. 100–07, 108–22, 460–75.
• Сотой, Маркус Дю. (2003). Музыка простых чисел . Нью-Йорк: Perennial-HarperCollins. ISBN 9780066210704.
• Стэнли, Ричард П. (1999). Перечислительная комбинаторика. Том. 1 и 2. Издательство Кембриджского университета. ISBN 0-521-56069-1.
• Уайтмен, Алабама (1956). «Сумма, связанная с рядом статистической суммы». Тихоокеанский математический журнал . 6 (1): 159–176. дои : 10.2140/pjm.1956.6.159 . Збл  0071.04004. (Обеспечивает формулу Сельберга. Более старая форма — это конечное разложение Фурье Сельберга.)

Внешние ссылки

• «Раздел», Математическая энциклопедия , EMS Press , 2001 [1994]
• Калькулятор разделов и составов
• Вайсштейн, Эрик В. «Перегородка». Математический мир .
• Уилф, Герберт С. Лекции о целочисленных разделах (PDF) , заархивировано (PDF) из оригинала 24 февраля 2021 г. , получено 28 февраля 2021 г.
• Счет с разбиениями со ссылками на таблицы в Электронной энциклопедии целочисленных последовательностей.
• Запись о целочисленных разделах в базе данных FindStat
• Модуль Integer::Partition Perl из CPAN
• Быстрые алгоритмы создания целочисленных разделов
• Генерация всех разделов: сравнение двух кодировок
• Грайм, Джеймс (28 апреля 2016 г.). «Перегородки — Числофил» (видео) . Брэйди Харан . Архивировано из оригинала 11 декабря 2021 г. Проверено 5 мая 2016 г.