Уравнение Ван 'т-Гоффа

Связь между температурой и константой равновесия химической реакции

Уравнение Вант-Гоффа связывает изменение константы равновесия , K _eq , химической реакции с изменением температуры , T , учитывая стандартное изменение энтальпии , Δ _r H ^⊖ , для процесса. Нижний индекс означает «реакция», а верхний индекс означает «стандарт». Оно было предложено голландским химиком Якобусом Хенрикусом ван-Гоффом в 1884 году в его книге Études de Dynamique chimique ( Исследования по динамической химии ). ^[1] ${\displaystyle r}$ ${\displaystyle \ominus }$

Уравнение Вант-Гоффа широко используется для исследования изменений функций состояния в термодинамической системе . График Вант-Гоффа , который выводится из этого уравнения, особенно эффективен для оценки изменения энтальпии и энтропии химической реакции .

Уравнение

Резюме и применение

Стандартное давление , , используется для определения исходного состояния для уравнения Вант-Гоффа, которое имеет вид ^{[2] [3]} ${\displaystyle P^{0}}$

${\displaystyle {\frac {d}{dT}}\ln K_{\mathrm {eq} }={\frac {\Delta _{r}H^{\ominus }}{RT^{2}}}}$

где ln обозначает натуральный логарифм , — термодинамическая константа равновесия , а R — идеальная газовая постоянная . Это уравнение является точным при любой температуре и всех давлениях, выведенных из требования, чтобы свободная энергия Гиббса реакции была стационарной в состоянии химического равновесия . ${\displaystyle K_{eq}}$

На практике уравнение часто интегрируется между двумя температурами, предполагая, что стандартная энтальпия реакции постоянна (и, кроме того, она также часто предполагается равной своему значению при стандартной температуре ). Поскольку в реальности и стандартная энтропия реакции изменяются с температурой для большинства процессов, ^[4] интегрированное уравнение является лишь приближенным. На практике также делаются приближения к коэффициентам активности в пределах константы равновесия. ${\displaystyle \Delta _{r}H^{\ominus }}$ ${\displaystyle \Delta _{r}H^{\ominus }}$ ${\displaystyle \Delta _{r}S^{\ominus }}$

Основное применение интегрированного уравнения заключается в оценке новой константы равновесия при новой абсолютной температуре , предполагающей постоянное изменение стандартной энтальпии в диапазоне температур. Чтобы получить интегрированное уравнение, удобно сначала переписать уравнение Ван 'т-Гоффа как ^[2]

${\displaystyle {\frac {d\ln K_{\mathrm {eq} }}{d{\frac {1}{T}}}}=-{\frac {\Delta _{r}H^{\ominus }}{R}}.}$

Определенный интеграл между температурами T ₁ и T ₂ тогда равен

${\displaystyle \ln {\frac {K_{2}}{K_{1}}}={\frac {\Delta _{r}H^{\ominus }}{R}}\left({\frac {1}{T_{1}}}-{\frac {1}{T_{2}}}\right).}$

В этом уравнении K ₁ — константа равновесия при абсолютной температуре T ₁ , а K ₂ — константа равновесия при абсолютной температуре T ₂ .

Развитие термодинамики

Объединяя известную формулу для свободной энергии Гиббса реакции

${\displaystyle \Delta _{r}G^{\ominus }=\Delta _{r}H^{\ominus }-T\Delta _{r}S^{\ominus },}$

где S — энтропия системы, с уравнением изотермы свободной энергии Гиббса: ^[5]

${\displaystyle \Delta _{r}G^{\ominus }=-RT\ln K_{\mathrm {eq} },}$

мы получаем

${\displaystyle \ln K_{\mathrm {eq} }=-{\frac {\Delta _{r}H^{\ominus }}{RT}}+{\frac {\Delta _{r}S^{\ominus }}{R}}.}$

Дифференцирование этого выражения по переменной T при допущении, что и не зависят от T, дает уравнение Ван 'т-Гоффа. Ожидается, что эти предположения несколько нарушатся при больших колебаниях температуры. ${\displaystyle \Delta _{r}H^{\ominus }}$ ${\displaystyle \Delta _{r}S^{\ominus }}$

При условии, что и являются постоянными, предыдущее уравнение дает ln K как линейную функцию ⁠ ${\displaystyle \Delta _{r}H^{\ominus }}$ ${\displaystyle \Delta _{r}S^{\ominus }}$1/Т⁠ и, следовательно, известна как линейная форма уравнения Вант-Гоффа. Следовательно, когда диапазон температур достаточно мал, чтобы стандартная энтальпия реакции и энтропия реакции были по существу постоянными, график натурального логарифма константы равновесия против обратной температуры дает прямую линию. Наклон линии можно умножить на газовую постоянную R , чтобы получить стандартное изменение энтальпии реакции, а отсекаемый элемент можно умножить на R, чтобы получить стандартное изменение энтропии .

Изотерма Вант-Гоффа

Изотерму Вант-Гоффа можно использовать для определения температурной зависимости свободной энергии Гиббса реакции для нестандартных состояний реакций при постоянной температуре: ^[6]

${\displaystyle \left({\frac {dG}{d\xi }}\right)_{T,p}=\Delta _{\mathrm {r} }G=\Delta _{\mathrm {r} }G^{\ominus }+RT\ln Q_{\mathrm {r} },}$

где — свободная энергия Гиббса реакции в нестандартных состояниях при температуре , — свободная энергия Гиббса для реакции при , — степень реакции , а Q _r — термодинамический коэффициент реакции . Поскольку , температурная зависимость обоих членов может быть описана уравнениями Ван-т'Гоффа как функция T . Это находит применение в области электрохимии . в частности, при изучении температурной зависимости гальванических элементов. ${\displaystyle \Delta _{\mathrm {r} }G}$ ${\displaystyle T}$ ${\displaystyle \Delta _{r}G^{\ominus }}$ ${\displaystyle (T,P^{0})}$ ${\displaystyle \xi }$ ${\displaystyle \Delta _{r}G^{\ominus }=-RT\ln K_{eq}}$

Изотерму также можно использовать при фиксированной температуре для описания закона действующих масс . Когда реакция находится в равновесии , Q _r = K _eq и . В противном случае изотерма Вант-Гоффа предсказывает направление, в котором система должна сместиться для достижения равновесия; когда Δ _r G < 0 , реакция движется в прямом направлении, тогда как когда Δ _r G > 0 , реакция движется в обратном направлении. См. Химическое равновесие . ${\displaystyle \Delta _{\mathrm {r} }G=0}$

Сюжет Ван 'т Хоффа

Для обратимой реакции константа равновесия может быть измерена при различных температурах. Эти данные могут быть нанесены на график с ln K _eq на оси y и ⁠1/Т⁠ на оси x . Данные должны иметь линейную зависимость, уравнение которой можно найти, подгоняя данные с помощью линейной формы уравнения Ван 'т-Гоффа

${\displaystyle \ln K_{\mathrm {eq} }=-{\frac {\Delta _{r}H^{\ominus }}{RT}}+{\frac {\Delta _{r}S^{\ominus }}{R}}.}$

Этот график называется «графиком Ван 'т Хоффа» и широко используется для оценки энтальпии и энтропии химической реакции . Из этого графика, − ⁠ΔrH_​​/Р⁠ — наклон, и ⁠ΔrS_​​/Р⁠ — точка пересечения линейной аппроксимации.

Измеряя константу равновесия , K _eq , при различных температурах, график Вант-Гоффа можно использовать для оценки реакции при изменении температуры. ^{[7] [8]} Зная наклон и отсекаемый отрезок графика Вант-Гоффа, можно легко получить энтальпию и энтропию реакции, используя

${\displaystyle {\begin{aligned}\Delta _{r}H&=-R\times {\text{slope}},\\\Delta _{r}S&=R\times {\text{intercept}}.\end{aligned}}}$

График Вант-Гоффа можно использовать для быстрого определения энтальпии химической реакции как качественно, так и количественно. Это изменение энтальпии может быть положительным или отрицательным, что приводит к двум основным формам графика Вант-Гоффа.

Эндотермические реакции

График Вант-Гоффа для эндотермической реакции

Для эндотермической реакции тепло поглощается, делая чистое изменение энтальпии положительным. Таким образом, согласно определению наклона:

${\displaystyle {\text{slope}}=-{\frac {\Delta _{r}H}{R}},}$

Когда реакция эндотермическая , ΔrH _> 0 (и газовая постоянная R > 0 ), поэтому

${\displaystyle {\text{slope}}=-{\frac {\Delta _{r}H}{R}}<0.}$

Таким образом, для эндотермической реакции график Вант-Гоффа всегда должен иметь отрицательный наклон.

Экзотермические реакции

График Вант-Гоффа для экзотермической реакции

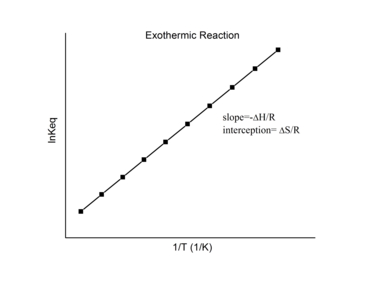
При экзотермической реакции выделяется тепло, что делает чистое изменение энтальпии отрицательным. Таким образом, согласно определению наклона:

${\displaystyle {\text{slope}}=-{\frac {\Delta _{r}H}{R}},}$

Для экзотермической реакции Δ _r H < 0 , поэтому

${\displaystyle {\text{slope}}=-{\frac {\Delta _{r}H}{R}}>0.}$

Таким образом, для экзотермической реакции график Вант-Гоффа всегда должен иметь положительный наклон.

Распространение ошибок

На первый взгляд, используя тот факт, что Δ _r G ^⊖ = − RT ln K = Δ _r H ^⊖ − T Δ _r S ^⊖, может показаться, что двух измерений K будет достаточно, чтобы получить точное значение Δ _r H ^⊖ :

${\displaystyle \Delta _{r}H^{\ominus }=R{\frac {\ln K_{1}-\ln K_{2}}{{\frac {1}{T_{2}}}-{\frac {1}{T_{1}}}}},}$

где K ₁ и K ₂ — значения констант равновесия, полученные при температурах T ₁ и T ₂ соответственно. Однако точность значений Δ _r H ^⊖, полученных таким образом, сильно зависит от точности измеренных значений констант равновесия.

Использование распространения ошибки показывает, что ошибка в Δ _r H ^⊖ будет составлять около 76 кДж/моль, умноженных на экспериментальную неопределенность в (ln K ₁ − ln K ₂ ) , или около 110 кДж/моль, умноженных на неопределенность в значениях ln K. Аналогичные соображения применимы к энтропии реакции, полученной из Δ _r S ^⊖ = ⁠1/Т⁠ (Δ H ^⊖ + RT ln K ) .

Примечательно, что когда константы равновесия измеряются при трех или более температурах, значения Δ _r H ^⊖ и Δ _r S ^⊖ часто получаются путем подгонки прямой линии . ^[9] Ожидается, что ошибка будет уменьшена с помощью этой процедуры, хотя предположение о том, что энтальпия и энтропия реакции постоянны, может оказаться верным, а может и нет. Если есть значительная температурная зависимость в одной или обеих величинах, она должна проявиться в нелинейном поведении на графике Ван 'т-Гоффа; однако, по-видимому, для наблюдения этого потребуется более трех точек данных.

Применение графика Вант-Гоффа

Анализ Ван 'т Хоффа

Анализ Ван 'т Хоффа

В биологических исследованиях график Ван 'т Хоффа также называется анализом Ван 'т Хоффа. ^[10] Он наиболее эффективен для определения предпочтительного продукта в реакции. Он может давать результаты, отличающиеся от результатов прямой калориметрии, такой как дифференциальная сканирующая калориметрия или изотермическая титрационная калориметрия, из-за различных эффектов, отличных от экспериментальной ошибки. ^[11]

Предположим, что в результате реакции образуются два продукта B и C:

а А + г Д → б В,

а А + г Д → в С.

В этом случае K _eq можно определить как отношение B к C, а не как константу равновесия.

Когда ⁠Б/С⁠ > 1, B является предпочтительным продуктом, и данные на графике Вант-Гоффа будут находиться в положительной области.

Когда ⁠Б/С⁠ < 1, C является предпочтительным продуктом, и данные на графике Вант-Гоффа будут находиться в отрицательной области.

Используя эту информацию, анализ Вант-Гоффа может помочь определить наиболее подходящую температуру для нужного продукта.

В 2010 году анализ Вант-Гоффа был использован для определения того, образует ли вода предпочтительно водородную связь с C -концом или N -концом аминокислоты пролина. ^[12] Константа равновесия для каждой реакции была найдена при различных температурах, и был создан график Вант-Гоффа. Этот анализ показал, что энтальпически вода предпочитала образовывать водородную связь с C -концом, но энтропийно она была более выгодна для водородной связи с N -концом. В частности, они обнаружили, что водородная связь C -конца была благоприятствована 4,2–6,4 кДж/моль. Водородная связь N -конца была благоприятствована 31–43 Дж/(К моль).

Эти данные сами по себе не могли сделать вывод о том, с каким сайтом вода будет предпочтительно связываться водородом, поэтому были проведены дополнительные эксперименты. Было установлено, что при более низких температурах предпочтительным был энтальпийно благоприятный вид, вода, связанная водородом с C -концом. При более высоких температурах предпочтительным был энтропийно благоприятный вид, вода, связанная водородом с N -концом.

Механистические исследования

График Вант-Гоффа в исследовании механизма

Химическая реакция может протекать по разным механизмам при разных температурах. ^[13]

В этом случае может быть использован график Ван 'т Гоффа с двумя или более линейными аппроксимациями. Каждый линейный аппроксиматор имеет разный наклон и точку пересечения, что указывает на разные изменения энтальпии и энтропии для каждого отдельного механизма. График Ван 'т Гоффа может быть использован для нахождения изменения энтальпии и энтропии для каждого механизма и предпочтительного механизма при разных температурах.

${\displaystyle {\begin{aligned}\Delta _{r}H_{1}&=-R\times {\text{slope}}_{1},&\Delta _{r}S_{1}&=R\times {\text{intercept}}_{1};\\[5pt]\Delta _{r}H_{2}&=-R\times {\text{slope}}_{2},&\Delta _{r}S_{2}&=R\times {\text{intercept}}_{2}.\end{aligned}}}$

На рисунке в качестве примера реакция протекает по механизму 1 при высокой температуре и по механизму 2 при низкой температуре.

Температурная зависимость

График зависимости Ван 'т-Гоффа от температуры

Если энтальпия и энтропия примерно постоянны при изменении температуры в определенном диапазоне, то график Ван 'т-Гоффа приблизительно линеен при построении в этом диапазоне. Однако в некоторых случаях энтальпия и энтропия действительно резко меняются с температурой. Приближение первого порядка заключается в предположении, что два разных продукта реакции имеют разные теплоемкости. Включение этого предположения дает дополнительный член ⁠с/Т ²⁠ в выражении для константы равновесия как функции температуры. Затем полиномиальная подгонка может быть использована для анализа данных, которые демонстрируют непостоянную стандартную энтальпию реакции: ^[14]

${\displaystyle \ln K_{\mathrm {eq} }=a+{\frac {b}{T}}+{\frac {c}{T^{2}}},}$

где

${\displaystyle {\begin{aligned}\Delta _{r}H&=-R\left(b+{\frac {2c}{T}}\right),\\\Delta _{r}S&=R\left(a-{\frac {c}{T^{2}}}\right).\end{aligned}}}$

Таким образом, энтальпию и энтропию реакции можно определить при определенных температурах, даже если существует температурная зависимость.

Самоорганизация поверхностно-активных веществ

Соотношение Вант-Гоффа особенно полезно для определения энтальпии мицеллообразования Δ H^⊖
_мповерхностно-активных веществ по температурной зависимости критической концентрации мицеллообразования (ККМ):

${\displaystyle {\frac {d}{dT}}\ln \mathrm {CMC} ={\frac {\Delta H_{\mathrm {m} }^{\ominus }}{RT^{2}}}.}$

Однако это соотношение теряет свою силу, когда число агрегации также зависит от температуры, и вместо него следует использовать следующее соотношение: ^[15]

${\displaystyle RT^{2}\left({\frac {\partial }{\partial T}}\ln \mathrm {CMC} \right)_{P}=-\Delta _{r}H_{\mathrm {m} }^{\ominus }(N)+T\left({\frac {\partial }{\partial N}}\left(G_{N+1}-G_{N}\right)\right)_{T,P}\left({\frac {\partial N}{\partial T}}\right)_{P},}$

где G _{N + 1} и G _N — свободные энергии поверхностно-активного вещества в мицелле с числом агрегации N + 1 и N соответственно. Этот эффект особенно актуален для неионных этоксилированных поверхностно-активных веществ ^[16] или блок-сополимеров полиоксипропилена и полиоксиэтилена (полоксамеры, плюроники, синпероники). ^[17] Расширенное уравнение можно использовать для извлечения чисел агрегации самоорганизующихся мицелл из дифференциальных сканирующих калориметрических термограмм. ^[18]

Смотрите также

• Соотношение Клаузиуса–Клапейрона
• Фактор Вант-Гоффа ( i )
• Уравнение Гиббса–Гельмгольца
• Равновесие растворимости
• Уравнение Аррениуса

Ссылки

1. Биография на сайте Нобелевской премии. Nobelprize.org (1 марта 1911 г.). Получено 08.11.2013.
2. Аткинс, Питер; Де Паула, Хулио (10 марта 2006 г.). Физическая химия (8-е изд.). WH Freeman and Company. стр. 212. ISBN 978-0-7167-8759-4.
3. Айвс, DJG (1971). Химическая термодинамика . Университетская химия. Macdonald Technical and Scientific. ISBN 978-0-356-03736-3.
4. Крейг, Норман (1996). «Диаграммы энтропии». J. Chem. Educ . 73 (8): 710. Bibcode : 1996JChEd..73..710C. doi : 10.1021/ed073p710.
5. Дикерсон, Р. Э.; Гейс, И. (1976). Химия, материя и Вселенная . США: WA Benjamin Inc. ISBN 978-0-19-855148-5.
6. Монк, Пол (2004). Физическая химия: понимание нашего химического мира . Wiley. стр. 162. ISBN 978-0471491811.
7. Ким, Тэ Ву (2012). «Динамическая [2]катенция самоорганизующихся макроциклов Pd(II) в воде». Chem. Lett . 41 : 70. doi :10.1246/cl.2012.70.
8. Ичикава, Такаюки (2010). "Термодинамические свойства амидов металлов, определяемые изотермами давления аммиака-состава" (PDF) . J. Chem. Thermodynamics . 42 : 140. doi :10.1016/j.jct.2009.07.024.
9. Чанг, Рэймонд; Томан, младший, Джон В. (2014). Физическая химия для химических наук . США: University Science Books. стр. 322–325. ISBN 978-1-891389-69-6.
10. «Анализ Ван 'т Хоффа». Группа анализа и проектирования белков.
11. Купер, Алан (2018), Робертс, Гордон; Уоттс, Энтони (ред.), «Анализ Вант-Гоффа и скрытые термодинамические переменные», Энциклопедия биофизики , Берлин, Гейдельберг: Springer, стр. 1–4, doi :10.1007/978-3-642-35943-9_10066-1, ISBN 978-3-642-35943-9, получено 4 июля 2023 г.
12. Прелл, Джеймс; Уильямс Э. (2010). «Энтропия перемещает присоединенную молекулу воды от C -конца к N -концу протонированного пролина». J. Am. Chem. Soc . 132 (42): 14733–5. doi :10.1021/ja106167d. PMID  20886878.
13. Чатаке, Тошиюки (2010). «Подход к кристаллизации ДНК с использованием термически обратимого процесса ДНК-дуплексов». Cryst. Growth Des . 10 (3): 1090. doi :10.1021/cg9007075.
14. Дэвид, Виктор (28 апреля 2011 г.). «Отклонение от зависимости Ван 'т Гоффа в RP-LC, вызванное таутомерным взаимопревращением, наблюдаемое для четырех соединений». Journal of Separation Science . 34 (12): 1423–8. doi :10.1002/jssc.201100029. PMID  21538875.
15. Хольцер, Альфред; Хольцер, Мэрилин Ф. (1 мая 2002 г.). «Использование соотношения Вант-Гоффа при определении энтальпии образования мицелл». Журнал физической химии . 78 (14): 1442–1443. doi :10.1021/j100607a026.
16. Heerklotz, Heiko; Tsamaloukas, Alekos; Kita-Tokarczyk, Katarzyna; Strunz, Pavel; Gutberlet, Thomas (25 ноября 2004 г.). «Структурная, объемная и термодинамическая характеристика перехода мицеллярной сферы в стержень». Журнал Американского химического общества . 126 (50): 16544–16552. doi :10.1021/ja045525w. PMID  15600359.
17. Табоада, Пабло; Москера, Виктор; Эттвуд, Дэвид; Янг, Чжо; Бут, Колин (5 июня 2003 г.). «Энтальпия мицеллизации диблочного сополи(оксиэтилена/оксипропилена) методом изотермической титрационной калориметрии. Сравнение со значением Ван 'т-Гоффа». Физическая химия Химическая физика . 5 (12): 2625–2627. Bibcode : 2003PCCP....5.2625T. doi : 10.1039/b303108j.
18. Chiappisi, Leonardo; Lazzara, Giuseppe; Gradzielski, Michael; Milioto, Stefana (6 декабря 2012 г.). «Количественное описание термограмм самоагрегации, вызванной температурой, определенных с помощью дифференциальной сканирующей калориметрии» (PDF) . Langmuir . 28 (51): 17609–17616. doi :10.1021/la303599d. hdl : 10447/96872 . PMID  23171124.