stringtranslate.com

Сверхпроводимость

Высокотемпературный сверхпроводник, парящий над магнитом. Постоянный электрический ток течет по поверхности сверхпроводника, исключая магнитное поле магнита ( эффект Мейсснера ). Этот ток фактически образует электромагнит, который отталкивает магнит.

Сверхпроводимость — это набор физических свойств, наблюдаемых в сверхпроводниках : материалах, где электрическое сопротивление исчезает, а магнитные поля вытесняются из материала. В отличие от обычного металлического проводника , сопротивление которого постепенно уменьшается по мере понижения его температуры, даже почти до абсолютного нуля , сверхпроводник имеет характерную критическую температуру, ниже которой сопротивление резко падает до нуля. [1] [2] Электрический ток через петлю сверхпроводящего провода может сохраняться бесконечно долго без источника питания. [3] [4] [5] [6]

Явление сверхпроводимости было открыто в 1911 году голландским физиком Хайке Камерлинг-Оннесом . Подобно ферромагнетизму и атомным спектральным линиям , сверхпроводимость является явлением, которое может быть объяснено только квантовой механикой . Оно характеризуется эффектом Мейсснера , полным погашением магнитного поля внутри сверхпроводника при его переходах в сверхпроводящее состояние. Возникновение эффекта Мейсснера указывает на то, что сверхпроводимость нельзя понимать просто как идеализацию идеальной проводимости в классической физике .

В 1986 году было обнаружено, что некоторые керамические материалы на основе купрата - перовскита имеют критическую температуру выше 90 К (-183 °C). [7] Такая высокая температура перехода теоретически невозможна для обычного сверхпроводника , что привело к тому, что материалы стали называть высокотемпературными сверхпроводниками . Дешевый доступный хладагент жидкий азот кипит при 77 К (-196 °C), и, таким образом, существование сверхпроводимости при более высоких температурах, чем эта, облегчает многие эксперименты и приложения, которые менее практичны при более низких температурах.

История

Хайке Камерлинг-Оннес (справа), первооткрыватель сверхпроводимости. Пауль Эренфест , Хендрик Лоренц , Нильс Бор стоят слева от него.

Сверхпроводимость была открыта 8 апреля 1911 года Хайке Камерлинг-Оннесом, который изучал сопротивление твердой ртути при криогенных температурах, используя недавно полученный жидкий гелий в качестве хладагента . [8] При температуре 4,2 К он заметил, что сопротивление резко исчезло. [9] В том же эксперименте он также наблюдал сверхтекучий переход гелия при 2,2 К, не осознавая его значения. Точная дата и обстоятельства открытия были восстановлены только столетие спустя, когда была найдена записная книжка Оннеса. [10] В последующие десятилетия сверхпроводимость наблюдалась в нескольких других материалах. В 1913 году было обнаружено, что свинец обладает сверхпроводимостью при 7 К, а в 1941 году было обнаружено, что нитрид ниобия обладает сверхпроводимостью при 16 К.

Большие усилия были направлены на то, чтобы выяснить, как и почему работает сверхпроводимость; важный шаг был сделан в 1933 году, когда Мейсснер и Оксенфельд обнаружили, что сверхпроводники вытесняют приложенные магнитные поля, явление, которое стало известно как эффект Мейсснера. [11] В 1935 году Фриц и Хайнц Лондон показали, что эффект Мейсснера является следствием минимизации электромагнитной свободной энергии, переносимой сверхпроводящим током. [12]

Лондонские материальные уравнения

Теоретическая модель, которая была впервые задумана для сверхпроводимости, была полностью классической: она суммируется с помощью основных уравнений Лондона . Она была выдвинута братьями Фрицем и Хайнцем Лондоном в 1935 году, вскоре после открытия того, что магнитные поля вытесняются из сверхпроводников. Главным триумфом уравнений этой теории является их способность объяснить эффект Мейсснера [11] , в котором материал экспоненциально вытесняет все внутренние магнитные поля, когда он пересекает порог сверхпроводимости. Используя уравнение Лондона, можно получить зависимость магнитного поля внутри сверхпроводника от расстояния до поверхности. [13]

Два основных уравнения для сверхпроводника по Лондону:

Первое уравнение следует из второго закона Ньютона для сверхпроводящих электронов.

Традиционные теории (1950-е годы)

В 1950-х годах физики-теоретики , занимающиеся конденсированными средами , пришли к пониманию «обычной» сверхпроводимости с помощью пары замечательных и важных теорий: феноменологической теории Гинзбурга–Ландау (1950) и микроскопической теории БКШ (1957). [14] [15]

В 1950 году Ландау и Гинзбург разработали феноменологическую теорию сверхпроводимости Гинзбурга–Ландау . [16] Эта теория, объединившая теорию фазовых переходов второго рода Ландау с волновым уравнением типа Шредингера , имела большой успех в объяснении макроскопических свойств сверхпроводников. В частности, Абрикосов показал, что теория Гинзбурга–Ландау предсказывает разделение сверхпроводников на две категории, которые теперь называются Тип I и Тип II. Абрикосов и Гинзбург были удостоены Нобелевской премии 2003 года за свою работу (Ландау получил Нобелевскую премию 1962 года за другую работу и умер в 1968 году). Четырехмерное расширение теории Гинзбурга–Ландау, модель Коулмена–Вайнберга , играет важную роль в квантовой теории поля и космологии .

Также в 1950 году Максвелл и Рейнольдс с соавторами обнаружили, что критическая температура сверхпроводника зависит от изотопной массы составляющего его элемента. [17] [18] Это важное открытие указало на электрон - фононное взаимодействие как на микроскопический механизм, ответственный за сверхпроводимость.

Полная микроскопическая теория сверхпроводимости была окончательно предложена в 1957 году Бардином , Купером и Шриффером . [15] Эта теория БКШ объясняла сверхпроводящий ток как сверхтекучую жидкость куперовских пар, пар электронов, взаимодействующих посредством обмена фононами. За эту работу авторы были удостоены Нобелевской премии в 1972 году.

Теория БКШ получила более прочную основу в 1958 году, когда Н. Н. Боголюбов показал, что волновая функция БКШ, первоначально полученная из вариационного аргумента, может быть получена с помощью канонического преобразования электронного гамильтониана . [19] В 1959 году Лев Горьков показал, что вблизи критической температуры теория БКШ сводится к теории Гинзбурга–Ландау. [20] [21]

Обобщения теории БКШ для обычных сверхпроводников составляют основу понимания явления сверхтекучести , поскольку они попадают в класс универсальности лямбда-перехода . Степень, в которой такие обобщения могут быть применены к нетрадиционным сверхпроводникам, до сих пор остается спорной.

Дальнейшая история

Первое практическое применение сверхпроводимости было получено в 1954 году, когда Дадли Аллен Бак изобрел криотрон . [ 22] Два сверхпроводника с существенно разными значениями критического магнитного поля были объединены для создания быстрого и простого переключателя для компьютерных элементов.

Вскоре после открытия сверхпроводимости в 1911 году Камерлинг-Оннес попытался создать электромагнит со сверхпроводящими обмотками, но обнаружил, что относительно слабые магнитные поля разрушают сверхпроводимость в исследованных им материалах. Гораздо позже, в 1955 году, GB Yntema [23] удалось построить небольшой 0,7-тесла-железный электромагнит с обмотками из сверхпроводящей ниобиевой проволоки. Затем, в 1961 году, JE Kunzler , E. Buehler, FSL Hsu и JH Wernick [24] сделали поразительное открытие, что при 4,2 кельвина ниобий-олово , соединение, состоящее из трех частей ниобия и одной части олова, способно поддерживать плотность тока более 100 000 ампер на квадратный сантиметр в магнитном поле 8,8 тесла. Несмотря на свою хрупкость и сложность в изготовлении, сплав ниобия и олова с тех пор оказался чрезвычайно полезным в супермагнитах, генерирующих магнитные поля до 20 тесла. В 1962 году TG Berlincourt и RR Hake [25] [26] обнаружили, что более пластичные сплавы ниобия и титана подходят для применений до 10 тесла. Вскоре после этого в Westinghouse Electric Corporation и Wah Chang Corporation началось коммерческое производство проволоки для супермагнитов из ниобия и титана . Хотя сплав ниобия и титана может похвастаться менее впечатляющими сверхпроводящими свойствами, чем сплав ниобия и олова, сплав ниобия и титана, тем не менее, стал наиболее широко используемым материалом для супермагнитов «рабочей лошадки», в значительной степени благодаря его очень высокой пластичности и простоте изготовления. Однако как ниобий-олово, так и ниобий-титан широко применяются в медицинских томографах МРТ, изгибающих и фокусирующих магнитах для огромных ускорителей частиц высокой энергии и множестве других приложений. Conectus, европейский консорциум по сверхпроводимости, подсчитал, что в 2014 году глобальная экономическая деятельность, для которой сверхпроводимость была незаменима, составила около пяти миллиардов евро, причем на системы МРТ приходилось около 80% от этой суммы.

В 1962 году Джозефсон сделал важное теоретическое предсказание, что сверхток может течь между двумя кусками сверхпроводника, разделенными тонким слоем изолятора. [27] Это явление, теперь называемое эффектом Джозефсона , используется в сверхпроводящих устройствах, таких как СКВИДы . Оно используется в наиболее точных доступных измерениях кванта магнитного потока Φ 0  =  h /(2 e ), где h — постоянная Планка . В сочетании с квантовым сопротивлением Холла это приводит к точному измерению постоянной Планка. Джозефсон был удостоен Нобелевской премии за эту работу в 1973 году. [28]

В 2008 году было высказано предположение, что тот же механизм, который создает сверхпроводимость, может создавать состояние суперизолятора в некоторых материалах с почти бесконечным электрическим сопротивлением . [29] Первая разработка и исследование сверхпроводящего конденсата Бозе-Эйнштейна (БЭК) в 2020 году предполагает, что существует «плавный переход между» режимами БЭК и Бардина-Купера-Шриффера . [30] [31]

Классификация

Существует множество критериев, по которым классифицируются сверхпроводники. Наиболее распространенными являются:

Реакция на магнитное поле

Сверхпроводник может быть Типа I , то есть иметь одно критическое поле , выше которого вся сверхпроводимость теряется, а ниже которого магнитное поле полностью вытесняется из сверхпроводника; или Типа II , то есть иметь два критических поля, между которыми допускается частичное проникновение магнитного поля через изолированные точки. [32] Эти точки называются вихрями . [33] Кроме того, в многокомпонентных сверхпроводниках возможна комбинация двух поведений. В этом случае сверхпроводник относится к Типу 1.5 . [34]

По теории действия

Сверхпроводник является обычным , если он управляется электрон-фононным взаимодействием и объясняется обычной теорией БКШ или ее расширением, теорией Элиашберга. В противном случае он является нетрадиционным . [35] [36] С другой стороны, сверхпроводник называется нетрадиционным, если сверхпроводящий параметр порядка преобразуется в соответствии с нетривиальным неприводимым представлением точечной группы или пространственной группы системы. [37]

По критической температуре

Сверхпроводник обычно считается высокотемпературным , если он достигает сверхпроводящего состояния выше температуры 30 К (−243,15 °C); [38] как в первоначальном открытии Георга Беднорца и К. Алекса Мюллера . [7] Это может также относиться к материалам, которые переходят в сверхпроводимость при охлаждении с использованием жидкого азота — то есть только при T c  > 77 К, хотя это обычно используется только для того, чтобы подчеркнуть, что жидкого азота в качестве охладителя достаточно. Низкотемпературные сверхпроводники относятся к материалам с критической температурой ниже 30 К и охлаждаются в основном жидким гелием ( T c  > 4,2 К). Одним из исключений из этого правила является группа сверхпроводников пниктида железа , которые демонстрируют поведение и свойства, типичные для высокотемпературных сверхпроводников, однако некоторые из этой группы имеют критические температуры ниже 30 К.

По материалу

Вверху: Периодическая таблица сверхпроводящих элементарных твердых тел и их экспериментальная критическая температура (T)
Внизу: Периодическая таблица сверхпроводящих бинарных гидридов (0–300 ГПа). Теоретические предсказания обозначены синим цветом, а экспериментальные результаты — красным [39]

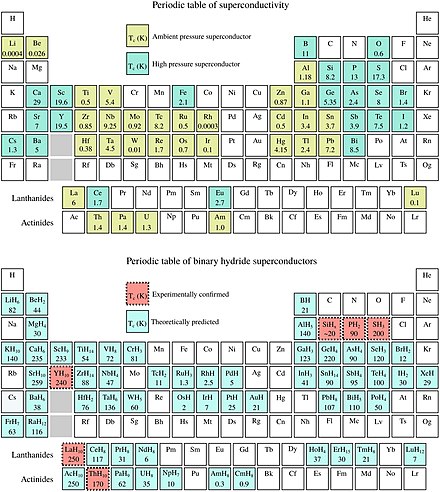
Классы сверхпроводящих материалов включают химические элементы (например, ртуть или свинец ), сплавы (такие как ниобий-титан , германий-ниобий и нитрид ниобия ), керамику ( YBCO и диборид магния ), сверхпроводящие пниктиды (например, легированный фтором LaOFeAs) или органические сверхпроводники ( фуллерены и углеродные нанотрубки ; хотя, возможно, эти примеры следует включить в число химических элементов, поскольку они полностью состоят из углерода ). [40] [41]

Элементарные свойства

Несколько физических свойств сверхпроводников различаются от материала к материалу, такие как критическая температура, значение сверхпроводящей щели , критическое магнитное поле и критическая плотность тока, при которой сверхпроводимость разрушается. С другой стороны, существует класс свойств, которые не зависят от основного материала. Эффект Мейсснера, квантование магнитного потока или постоянных токов, т. е. состояние нулевого сопротивления, являются наиболее важными примерами. Существование этих «универсальных» свойств коренится в природе нарушенной симметрии сверхпроводника и возникновении недиагонального дальнего порядка. Сверхпроводимость является термодинамической фазой и, таким образом, обладает определенными отличительными свойствами, которые в значительной степени не зависят от микроскопических деталей. Недиагональный дальний порядок тесно связан с образованием куперовских пар .

Нулевое электрическое сопротивление постоянному току

Электрические кабели для ускорителей в ЦЕРНе . Как массивные, так и тонкие кабели рассчитаны на 12 500 А. Вверху: обычные кабели для LEP ; внизу: кабели на основе сверхпроводников для LHC
Поперечное сечение предварительно сформированного сверхпроводящего стержня из заброшенного Техасского сверхпроводящего суперколлайдера (SSC)

Самый простой способ измерения электрического сопротивления образца некоторого материала — поместить его в электрическую цепь последовательно с источником тока I и измерить результирующее напряжение V на образце. Сопротивление образца определяется законом Ома как R = V / I. Если напряжение равно нулю, это означает, что сопротивление равно нулю.

Сверхпроводники также способны поддерживать ток без какого-либо приложенного напряжения, свойство, используемое в сверхпроводящих электромагнитах, таких как те, что используются в аппаратах МРТ . Эксперименты показали, что токи в сверхпроводящих катушках могут сохраняться годами без какой-либо измеримой деградации. Экспериментальные данные указывают на продолжительность жизни не менее 100 000 лет. Теоретические оценки продолжительности жизни постоянного тока могут превышать предполагаемую продолжительность жизни Вселенной в зависимости от геометрии провода и температуры. [5] На практике токи, введенные в сверхпроводящие катушки, сохранялись в течение 28 лет, 7 месяцев, 27 дней в сверхпроводящем гравиметре в Бельгии с 4 августа 1995 года по 31 марта 2024 года. [42] [43] В таких приборах измерение основано на мониторинге левитации сверхпроводящей ниобиевой сферы массой четыре грамма.

В обычном проводнике электрический ток можно представить как жидкость электронов, движущихся по тяжелой ионной решетке. Электроны постоянно сталкиваются с ионами в решетке, и во время каждого столкновения часть энергии, переносимой током, поглощается решеткой и преобразуется в тепло , которое по сути является колебательной кинетической энергией ионов решетки. В результате энергия, переносимая током, постоянно рассеивается. Это явление электрического сопротивления и джоулева нагрева .

В сверхпроводнике ситуация иная. В обычном сверхпроводнике электронная жидкость не может быть разделена на отдельные электроны. Вместо этого она состоит из связанных пар электронов, известных как куперовские пары . Это спаривание вызвано силой притяжения между электронами из-за обмена фононами . Это спаривание очень слабое, и небольшие тепловые колебания могут разрушить связь. Из-за квантовой механики энергетический спектр этой куперовской парной жидкости обладает энергетической щелью , что означает, что существует минимальное количество энергии Δ E , которое должно быть предоставлено для возбуждения жидкости. Следовательно, если Δ E больше тепловой энергии решетки, заданной kT , где k — постоянная Больцмана , а T — температура , жидкость не будет рассеиваться решеткой. [44] Таким образом, куперовская парная жидкость является сверхтекучей , то есть она может течь без рассеивания энергии.

В классе сверхпроводников, известных как сверхпроводники II типа , включая все известные высокотемпературные сверхпроводники , чрезвычайно низкое, но ненулевое удельное сопротивление появляется при температурах не слишком ниже номинального сверхпроводящего перехода, когда электрический ток применяется в сочетании с сильным магнитным полем, что может быть вызвано электрическим током. Это происходит из-за движения магнитных вихрей в электронной сверхтекучей жидкости, которое рассеивает часть энергии, переносимой током. Если ток достаточно мал, вихри неподвижны, и удельное сопротивление исчезает. Сопротивление, вызванное этим эффектом, ничтожно мало по сравнению с сопротивлением несверхпроводящих материалов, но его необходимо учитывать в чувствительных экспериментах. Однако, когда температура понижается достаточно далеко от номинального сверхпроводящего перехода, эти вихри могут застыть в неупорядоченной, но неподвижной фазе, известной как «вихревое стекло». Ниже этой температуры перехода в вихревое стекло сопротивление материала становится действительно нулевым.

Фазовый переход

Поведение теплоемкости ( c v , синий) и удельного сопротивления ( ρ , зеленый) при сверхпроводящем фазовом переходе

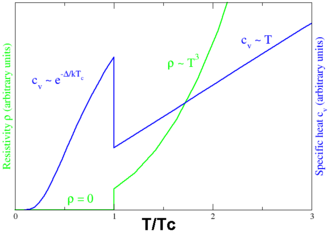
В сверхпроводящих материалах характеристики сверхпроводимости проявляются, когда температура T опускается ниже критической температуры T c . Значение этой критической температуры варьируется от материала к материалу. Обычные сверхпроводники обычно имеют критические температуры в диапазоне от около 20  К до менее 1 К. Твердая ртуть , например, имеет критическую температуру 4,2 К. По состоянию на 2015 год самая высокая критическая температура, обнаруженная для обычного сверхпроводника, составляет 203 К для H 2 S, хотя для этого требовались высокие давления около 90 гигапаскалей. [45] Купратные сверхпроводники могут иметь гораздо более высокие критические температуры: YBa 2 Cu 3 O 7 , один из первых обнаруженных купратных сверхпроводников, имеет критическую температуру выше 90 К, а купраты на основе ртути были обнаружены с критическими температурами, превышающими 130 К. Основной физический механизм, ответственный за высокую критическую температуру, пока не ясен. Однако ясно, что имеет место двухэлектронное спаривание, хотя природа спаривания ( волна против волны) остается спорной. [46]

Аналогично, при фиксированной температуре ниже критической температуры сверхпроводящие материалы перестают быть сверхпроводящими, когда применяется внешнее магнитное поле , которое больше критического магнитного поля . Это происходит потому, что свободная энергия Гиббса сверхпроводящей фазы увеличивается квадратично с магнитным полем, в то время как свободная энергия нормальной фазы примерно не зависит от магнитного поля. Если материал сверхпроводит в отсутствие поля, то свободная энергия сверхпроводящей фазы ниже, чем у нормальной фазы, и поэтому для некоторого конечного значения магнитного поля (пропорционального квадратному корню из разности свободных энергий при нулевом магнитном поле) две свободные энергии будут равны, и произойдет фазовый переход в нормальную фазу. В более общем случае, более высокая температура и более сильное магнитное поле приводят к меньшей доле электронов, которые являются сверхпроводящими, и, следовательно, к большей лондоновской глубине проникновения внешних магнитных полей и токов. Глубина проникновения становится бесконечной при фазовом переходе.

Возникновение сверхпроводимости сопровождается резкими изменениями различных физических свойств, что является отличительной чертой фазового перехода . Например, электронная теплоемкость пропорциональна температуре в нормальном (несверхпроводящем) режиме. При сверхпроводящем переходе она претерпевает скачок и после этого перестает быть линейной. При низких температурах она изменяется вместо этого как e − α / T для некоторой константы α . Это экспоненциальное поведение является одним из доказательств существования энергетической щели .

Порядок сверхпроводящего фазового перехода долгое время был предметом споров. Эксперименты показывают, что переход является переходом второго рода, то есть скрытой теплоты нет . Однако при наличии внешнего магнитного поля скрытая теплота есть, поскольку сверхпроводящая фаза имеет более низкую энтропию ниже критической температуры, чем нормальная фаза. Экспериментально было показано [47] , что, как следствие, когда магнитное поле увеличивается за пределами критического поля, результирующий фазовый переход приводит к снижению температуры сверхпроводящего материала.

Расчеты 1970-х годов показали, что он на самом деле может быть слабо первого порядка из-за эффекта дальнодействующих флуктуаций в электромагнитном поле. В 1980-х годах было теоретически показано с помощью теории поля беспорядка, в которой вихревые линии сверхпроводника играют главную роль, что переход является переходом второго порядка в режиме типа II и первого порядка (т. е. скрытого тепла ) в режиме типа I , и что эти две области разделены трикритической точкой . [48] Результаты были в значительной степени подкреплены компьютерным моделированием Монте-Карло. [49]

эффект Мейсснера

Эффект Мейсснера в высокотемпературном сверхпроводнике (черная гранула) с магнитом NdFeB (металлическим)

Когда сверхпроводник помещают в слабое внешнее магнитное поле H и охлаждают ниже температуры перехода, магнитное поле выбрасывается. Эффект Мейсснера не приводит к полному выбрасыванию поля, а вместо этого поле проникает в сверхпроводник, но только на очень малое расстояние, характеризуемое параметром  λ , называемым лондоновской глубиной проникновения , экспоненциально спадающей до нуля в объеме материала. Эффект Мейсснера является определяющей характеристикой сверхпроводимости. Для большинства сверхпроводников лондоновская глубина проникновения составляет порядка 100 нм.

Эффект Мейсснера иногда путают с видом диамагнетизма, который можно было бы ожидать в идеальном электрическом проводнике: согласно закону Ленца , когда к проводнику прикладывается изменяющееся магнитное поле, оно индуцирует в проводнике электрический ток, который создает противоположное магнитное поле. В идеальном проводнике может быть индуцирован произвольно большой ток, и результирующее магнитное поле в точности нейтрализует приложенное поле.

Эффект Мейсснера отличается от этого – это спонтанное выталкивание, которое происходит при переходе к сверхпроводимости. Предположим, что у нас есть материал в нормальном состоянии, содержащий постоянное внутреннее магнитное поле. Когда материал охлаждается ниже критической температуры, мы наблюдаем резкое выталкивание внутреннего магнитного поля, чего мы не ожидали бы, исходя из закона Ленца.

Феноменологическое объяснение эффекта Мейснера дали братья Фриц и Хайнц Лондоны , которые показали, что электромагнитная свободная энергия в сверхпроводнике минимизируется при условии, что где H — магнитное поле, а λ — глубина проникновения Лондона.

Это уравнение, известное как уравнение Лондона , предсказывает, что магнитное поле в сверхпроводнике затухает экспоненциально от любого значения, которым оно обладает на поверхности.

Сверхпроводник с небольшим или отсутствующим магнитным полем внутри находится в состоянии Мейсснера. Состояние Мейсснера разрушается, когда приложенное магнитное поле слишком велико. Сверхпроводники можно разделить на два класса в зависимости от того, как происходит этот разрыв. В сверхпроводниках I типа сверхпроводимость резко разрушается, когда напряженность приложенного поля превышает критическое значение H c . В зависимости от геометрии образца можно получить промежуточное состояние [50], состоящее из барочного узора [51] областей нормального материала, несущего магнитное поле, смешанного с областями сверхпроводящего материала, не содержащего поля. В сверхпроводниках II типа увеличение приложенного поля выше критического значения H c1 приводит к смешанному состоянию (также известному как вихревое состояние), в котором все большее количество магнитного потока проникает в материал, но не остается сопротивления потоку электрического тока, пока ток не слишком велик. При второй критической напряженности поля H c2 сверхпроводимость разрушается. Смешанное состояние на самом деле вызвано вихрями в электронной сверхтекучей жидкости, иногда называемыми флюксонами, поскольку поток, переносимый этими вихрями, квантуется . Большинство чистых элементарных сверхпроводников, за исключением ниобия и углеродных нанотрубок , относятся к типу I, тогда как почти все нечистые и составные сверхпроводники относятся к типу II.

Лондонский момент

Наоборот, вращающийся сверхпроводник генерирует магнитное поле, точно выровненное с осью вращения. Эффект, момент Лондона, был хорошо использован в Gravity Probe B. Этот эксперимент измерял магнитные поля четырех сверхпроводящих гироскопов, чтобы определить их оси вращения. Это было критически важно для эксперимента, поскольку это один из немногих способов точно определить ось вращения в противном случае безликой сферы.

Высокотемпературная сверхпроводимость

Хронология сверхпроводящих материалов. Цвета представляют различные классы материалов:

До 1986 года физики считали, что теория БКШ запрещает сверхпроводимость при температурах выше примерно 30 К. В том году Беднорц и Мюллер открыли сверхпроводимость в оксиде лантана, бария и меди (LBCO), купратном перовскитном материале на основе лантана , который имел температуру перехода 35 К (Нобелевская премия по физике, 1987). [7] Вскоре было обнаружено, что замена лантана на иттрий (т. е. создание YBCO) повысила критическую температуру выше 90 К. [52]

Этот температурный скачок имеет особое инженерное значение, поскольку он позволяет использовать жидкий азот в качестве хладагента, заменяя жидкий гелий. [52] Жидкий азот можно производить относительно дёшево, даже на месте. Более высокие температуры дополнительно помогают избежать некоторых проблем, которые возникают при температурах жидкого гелия, таких как образование пробок из замороженного воздуха, которые могут блокировать криогенные линии и вызывать непредвиденное и потенциально опасное повышение давления. [53] [54]

С тех пор было открыто много других купратных сверхпроводников, и теория сверхпроводимости в этих материалах является одной из главных нерешенных задач теоретической физики конденсированного состояния . [55] [56] В настоящее время существуют две основные гипотезы — теория резонирующей валентной связи и теория спиновой флуктуации, которая пользуется наибольшей поддержкой в ​​исследовательском сообществе. [57] Вторая гипотеза предполагает, что электронное спаривание в высокотемпературных сверхпроводниках опосредовано спиновыми волнами короткого радиуса действия, известными как парамагноны . [58] [59] [ сомнительно – обсудить ]

В 2008 году голографическая сверхпроводимость, которая использует голографическую дуальность или теорию соответствия AdS/CFT , была предложена Губсером, Хартноллом, Герцогом и Горовицем в качестве возможного объяснения высокотемпературной сверхпроводимости в некоторых материалах. [60]

Примерно с 1993 года самым высокотемпературным сверхпроводником был известный керамический материал, состоящий из ртути, бария, кальция, меди и кислорода (HgBa 2 Ca 2 Cu 3 O 8+δ ) с T c = 133–138 K. [ 61] [62]

В феврале 2008 года было открыто семейство высокотемпературных сверхпроводников на основе железа. [63] [64] Хидео Хосоно из Токийского технологического института и его коллеги обнаружили лантан-кислород-фтор-арсенид железа (LaO 1−x F x FeAs), оксипниктид , который обладает сверхпроводимостью ниже 26 К. Замена лантана в LaO 1− x F x FeAs на самарий приводит к сверхпроводникам, которые работают при 55 К. [65]

В 2014 и 2015 годах сероводород ( H
2S ) при чрезвычайно высоких давлениях (около 150 гигапаскалей) был впервые предсказан, а затем подтвержден как высокотемпературный сверхпроводник с температурой перехода 80 К. [66] [67] [68] Кроме того, в 2019 году было обнаружено, что гидрид лантана ( LaH
10) становится сверхпроводником при 250 К под давлением 170 гигапаскалей. [69] [68]

В 2018 году исследовательская группа из физического факультета Массачусетского технологического института обнаружила сверхпроводимость в двухслойном графене с одним слоем, скрученным под углом примерно 1,1 градуса при охлаждении и приложении небольшого электрического заряда. Даже если эксперименты не проводились в высокотемпературной среде, результаты меньше коррелируют с классическими, но высокотемпературными сверхпроводниками, учитывая, что не требуется вводить посторонние атомы. [70] Эффект сверхпроводимости возник в результате электронов, скрученных в вихрь между слоями графена, называемых « скирмионами ». Они действуют как одна частица и могут объединяться в пары по слоям графена, что приводит к основным условиям, необходимым для сверхпроводимости. [71]

В 2020 году в статье в Nature был описан сверхпроводник комнатной температуры (критическая температура 288 К), изготовленный из водорода, углерода и серы под давлением около 270 гигапаскалей . [72] [73] Однако в 2022 году статья была отозвана редакторами, поскольку обоснованность процедур вычитания фона была поставлена ​​под сомнение. Все девять авторов утверждают, что исходные данные убедительно подтверждают основные утверждения статьи. [74]

31 декабря 2023 года в журнале «Advanced Quantum Technologies» была опубликована статья «Глобальная сверхпроводимость при комнатной температуре в графите», в которой утверждается, что была продемонстрирована сверхпроводимость при комнатной температуре и давлении окружающей среды в высокоориентированном пиролитическом графите с плотными массивами почти параллельных линейных дефектов. [75]

Приложения

Видео сверхпроводящей левитации YBCO

Сверхпроводники являются перспективными кандидатами на роль материалов для разработки основных элементов схем электронных, спинтронных и квантовых технологий. Одним из таких примеров является сверхпроводящий диод, [76] в котором сверхток течет только в одном направлении, что обещает сверхпроводящие и гибридные технологии полупроводников-сверхпроводников без рассеивания.

Сверхпроводящие магниты являются одними из самых мощных известных электромагнитов . Они используются в машинах МРТ / ЯМР , масс-спектрометрах , магнитах управления лучом, используемых в ускорителях частиц , и магнитах, ограничивающих плазму в некоторых токамаках . Их также можно использовать для магнитного разделения, где слабомагнитные частицы извлекаются из фона менее или немагнитных частиц, как в пигментной промышленности. Их также можно использовать в больших ветряных турбинах для преодоления ограничений, накладываемых высокими электрическими токами, при этом сверхпроводящий ветряной генератор промышленного класса мощностью 3,6 мегаватта был успешно испытан в Дании. [77]

В 1950-х и 1960-х годах сверхпроводники использовались для создания экспериментальных цифровых компьютеров с использованием криотронных переключателей. [78] В последнее время сверхпроводники использовались для создания цифровых схем на основе быстрой однопоточной квантовой технологии, а также ВЧ- и СВЧ-фильтров для базовых станций мобильных телефонов .

Сверхпроводники используются для создания переходов Джозефсона , которые являются строительными блоками СКВИДов (сверхпроводящих квантовых интерференционных устройств), наиболее чувствительных известных магнитометров . СКВИДы используются в сканирующих микроскопах СКВИД и магнитоэнцефалографии . Серии устройств Джозефсона используются для реализации СИ вольт . Сверхпроводящие детекторы фотонов [79] могут быть реализованы в различных конфигурациях устройств. В зависимости от конкретного режима работы переход Джозефсона сверхпроводник-изолятор-сверхпроводник может использоваться как детектор фотонов или как смеситель . Большое изменение сопротивления при переходе из нормального в сверхпроводящее состояние используется для создания термометров в криогенных микрокалориметрических фотонных детекторах . Тот же эффект используется в сверхчувствительных болометрах, изготовленных из сверхпроводящих материалов. Сверхпроводящие нанопроволочные однофотонные детекторы обеспечивают высокоскоростное, малошумное однофотонное обнаружение и широко используются в передовых приложениях по подсчету фотонов . [80]

Возникают другие ранние рынки, где относительная эффективность, размер и весовые преимущества устройств, основанных на высокотемпературной сверхпроводимости, перевешивают дополнительные затраты. Например, в ветряных турбинах меньший вес и объем сверхпроводящих генераторов могут привести к экономии на строительстве и стоимости башни, компенсируя более высокие затраты на генератор и снижая общую приведенную стоимость электроэнергии (LCOE). [81]

Перспективные будущие приложения включают высокопроизводительную интеллектуальную сеть , передачу электроэнергии , трансформаторы , устройства хранения энергии , компактные устройства термоядерной энергии , электродвигатели (например, для движения транспортных средств, как в вакуумных поездах или поездах на магнитной подвеске ), устройства магнитной левитации , ограничители тока короткого замыкания , улучшение спинтронных устройств сверхпроводящими материалами [82] и сверхпроводящее магнитное охлаждение . Однако сверхпроводимость чувствительна к движущимся магнитным полям, поэтому приложения, которые используют переменный ток (например, трансформаторы), будет сложнее разрабатывать, чем те, которые полагаются на постоянный ток . По сравнению с традиционными линиями электропередач сверхпроводящие линии электропередачи более эффективны и требуют лишь часть пространства, что не только приведет к лучшим экологическим показателям, но и может улучшить общественное принятие расширения электросети. [83] Другим привлекательным промышленным аспектом является возможность передачи высокой мощности при более низких напряжениях. [84] Повышение эффективности систем охлаждения и использование дешевых охлаждающих жидкостей, таких как жидкий азот, также значительно снизили затраты на охлаждение, необходимое для сверхпроводимости.

Нобелевские премии

По состоянию на 2022 год было присуждено пять Нобелевских премий по физике за работы, связанные со сверхпроводимостью:

Смотрите также

Ссылки

  1. ^ Комбескот, Роланд (2022). Сверхпроводимость. Cambridge University Press. стр. 1–2. ISBN 9781108428415.
  2. ^ Фоссхейм, Кристиан; Садбо, Асл (2005). Сверхпроводимость: физика и приложения. John Wiley and Sons. стр. 7. ISBN 9780470026434.
  3. ^ Бардин, Джон; Купер, Леон; Шриффер, Дж. Р. (1 декабря 1957 г.). "Теория сверхпроводимости". Physical Review . 108 (5): 1175. Bibcode : 1957PhRv..108.1175B . doi : 10.1103/physrev.108.1175 . ISBN 978-0-677-00080-0. S2CID  73661301 . Получено 6 июня 2014 г. .Перепечатано в книге Николая Николаевича Боголюбова (1963) Теория сверхпроводимости, т. 4 , CRC Press, ISBN 0677000804 , стр. 73. 
  4. ^ Дейнтит, Джон (2009). Словарь фактов о файле физики (4-е изд.). Infobase Publishing. стр. 238. ISBN 978-1-4381-0949-7.
  5. ^ ab Gallop, John C. (1990). SQUIDS, эффекты Джозефсона и сверхпроводящая электроника. CRC Press . стр. 1, 20. ISBN 978-0-7503-0051-3.
  6. ^ Дюррант, Алан (2000). Квантовая физика материи. CRC Press. С. 102–103. ISBN 978-0-7503-0721-5.
  7. ^ abc Bednorz, JG & Müller, KA (1986). "Возможная сверхпроводимость при высоких температурах в системе Ba−La−Cu−O". Z. Phys. B . 64 (1): 189–193. Bibcode :1986ZPhyB..64..189B. doi :10.1007/BF01303701. S2CID  118314311.
  8. ^ Ван Делфт, Дирк; Кес, Питер (2010-09-01). «Открытие сверхпроводимости». Physics Today . 63 (9): 38–43. Bibcode : 2010PhT....63i..38V. doi : 10.1063/1.3490499 . ISSN  0031-9228.
  9. ^ Камерлинг-Оннес, Хайке (1911). «Дальнейшие эксперименты с жидким гелием. C. Об изменении электрического сопротивления чистых металлов при очень низких температурах и т. д. IV. Сопротивление чистой ртути при гелиевых температурах». Труды Секции наук . 13 : 1274–1276. Бибкод :1910KNAB...13.1274K.
  10. ^ ВанДелфт, Дирк; Кес, Питер (сентябрь 2010 г.). «Открытие сверхпроводимости» (PDF) . Physics Today . 63 (9): 38–43. Bibcode : 2010PhT....63i..38V. doi : 10.1063/1.3490499.
  11. ^ аб Мейснер, В. и Оксенфельд, Р. (1933). «Ein neuer Effekt bei Eintritt der Supraleitfähigkeit». Naturwissenschaften . 21 (44): 787–788. Бибкод : 1933NW.....21..787M. дои : 10.1007/BF01504252. S2CID  37842752.
  12. ^ Лондон, Ф. и Лондон, Х. (1935). «Электромагнитные уравнения сверхпроводника». Труды Лондонского королевского общества A. 149 ( 866): 71–88. Bibcode : 1935RSPSA.149...71L. doi : 10.1098/rspa.1935.0048. JSTOR  96265.
  13. ^ "Уравнения Лондона". Открытый университет. Архивировано из оригинала 23 декабря 2012 г. Получено 16 октября 2011 г.
  14. ^ Бардин, Дж.; Купер, Л. Н. и Шриффер, Дж. Р. (1957). «Микроскопическая теория сверхпроводимости». Physical Review . 106 (1): 162–164. Bibcode : 1957PhRv..106..162B. doi : 10.1103/PhysRev.106.162 .
  15. ^ ab Бардин, Дж.; Купер, Л. Н. и Шриффер, Дж. Р. (1957). «Теория сверхпроводимости». Physical Review . 108 (5): 1175–1205. Bibcode : 1957PhRv..108.1175B. doi : 10.1103/PhysRev.108.1175 .
  16. ^ Гинзбург, В.Л. и Ландау, Л.Д. (1950). «К теории сверхпроводимости». Журнал Экспериментальной и теоретической физики . 20 :1064.
  17. ^ Максвелл, Э. (1950). «Изотопный эффект в сверхпроводимости ртути». Physical Review . 78 (4): 477. Bibcode : 1950PhRv...78..477M. doi : 10.1103/PhysRev.78.477.
  18. ^ Рейнольдс, CA; Серин, B.; Райт, WH и Несбитт, LB (1950). "Сверхпроводимость изотопов ртути". Physical Review . 78 (4): 487. Bibcode : 1950PhRv...78..487R. doi : 10.1103/PhysRev.78.487.
  19. ^ Боголюбов, Н. Н. (1958). «Новый метод в теории сверхпроводимости». Журнал Экспериментальной и теоретической физики . 34:58 .
  20. ^ Горьков, Л. П. (1959). «Микроскопический вывод уравнений Гинзбурга–Ландау в теории сверхпроводимости». Журнал экспериментальной и теоретической физики . 36 : 1364.
  21. ^ Комбескот, М.; Погосов, В. В.; Бетбедер-Матибет, О. (2013). «Анзац БКШ для сверхпроводимости в свете подхода Боголюбова и точной волновой функции Ричардсона–Годена». Physica C: Сверхпроводимость . 485 : 47–57. arXiv : 1111.4781 . Bibcode : 2013PhyC..485...47C. doi : 10.1016/j.physc.2012.10.011. S2CID  119121639.
  22. ^ Бак, Дадли А. «Криотрон – сверхпроводящий компонент компьютера» (PDF) . Лаборатория Линкольна, Массачусетский технологический институт . Получено 10 августа 2014 г. .
  23. ^ Yntema, GB (1955). "Сверхпроводящая обмотка для электромагнита". Physical Review . 98 (4): 1197. Bibcode : 1955PhRv...98.1144.. doi : 10.1103/PhysRev.98.1144.
  24. ^ Кунцлер, Дж. Э.; Бюлер, Э.; Хсу, Ф. Л. С.; Верник, Дж. Х. (1961). «Сверхпроводимость в Nb3Sn при высокой плотности тока в магнитном поле 88 кГс». Physical Review Letters . 6 (3): 89–91. Bibcode : 1961PhRvL...6...89K. doi : 10.1103/PhysRevLett.6.89.
  25. ^ Berlincourt, TG & Hake, RR (1962). «Исследования сверхпроводящих сплавов переходных металлов с помощью импульсного магнитного поля при высоких и низких плотностях тока». Бюллетень Американского физического общества . II-7 : 408.
  26. ^ Berlincourt, TG (1987). "Появление Nb-Ti как сверхмагнитного материала" (PDF) . Криогеника . 27 (6): 283–289. Bibcode :1987Cryo...27..283B. doi :10.1016/0011-2275(87)90057-9.
  27. ^ Джозефсон, БД (1962). «Возможные новые эффекты в сверхпроводящем туннелировании». Physics Letters . 1 (7): 251–253. Bibcode : 1962PhL.....1..251J. doi : 10.1016/0031-9163(62)91369-0.
  28. ^ "Нобелевская премия по физике 1973 года". NobelPrize.org . Архивировано из оригинала 25 марта 2021 г. Получено 30 марта 2021 г.
  29. ^ "Было создано новое фундаментальное состояние материи — суперизолятор". Science Daily . 9 апреля 2008 г. Получено 23 октября 2008 г.
  30. ^ "Исследователи демонстрируют сверхпроводник, который ранее считался невозможным". phys.org . Получено 8 декабря 2020 г. .
  31. ^ Хасимото, Такахиро; Ота, Юичи; Цузуки, Акихиро; Нагашима, Цубаки; Фукусима, Акико; Касахара, Сигэру; Мацуда, Юджи; Мацуура, Кохей; Мизуками, Юта; Сибаучи, Такасада; Шин, Шик; Окадзаки, Кодзо (1 ноября 2020 г.). «Сверхпроводимость бозе-эйнштейновской конденсации, вызванная исчезновением нематического состояния». Достижения науки . 6 (45): eabb9052. Бибкод : 2020SciA....6.9052H. doi : 10.1126/sciadv.abb9052. ISSN  2375-2548. ПМЦ 7673702 . ПМИД  33158862. 
  32. ^ "Сверхпроводимость | ЦЕРН". home.cern . Получено 29.10.2020 .
  33. ^ Ортакер, Ангелина. "Сверхпроводимость" (PDF) . Технический университет Граца .
  34. ^ "Сверхпроводник типа 1.5 показывает свои полоски". Physics World . 2009-02-17 . Получено 2020-10-29 .
  35. ^ Гибни, Элизабет (5 марта 2018 г.). «Неожиданное открытие графена может раскрыть секреты сверхпроводимости». Новости. Nature . 555 (7695): 151–152. Bibcode :2018Natur.555..151G. doi : 10.1038/d41586-018-02773-w . PMID  29517044. Сверхпроводники в целом бывают двух типов: обычные, в которых активность можно объяснить с помощью общепринятой теории сверхпроводимости, и нетрадиционные, где это невозможно.
  36. ^ Hirsch, JE; Maple, MB; Marsiglio, F. (2015-07-15). "Классы сверхпроводящих материалов: Введение и обзор". Physica C: Сверхпроводимость и ее применение . Сверхпроводящие материалы: обычные, нетрадиционные и неопределенные. 514 : 1–8. arXiv : 1504.03318 . Bibcode :2015PhyC..514....1H. doi :10.1016/j.physc.2015.03.002. ISSN  0921-4534.
  37. ^ Минеев, ВП; Самохин, К (1999-09-21). Введение в нетрадиционную сверхпроводимость . Амстердам: CRC Press. стр. vii, 20. ISBN 978-90-5699-209-5.
  38. ^ Грант, Пол Майкл (2011). «Великая квантовая головоломка». Nature . 476 (7358). Nature Publishing Group, подразделение Macmillan Publishers Limited. Все права защищены.: 37–39. doi : 10.1038/476037a. PMID  21814269. S2CID  27665903.
  39. ^ Флорес-Ливас, Хосе А.; и др. (29 апреля 2020 г.). «Перспектива обычных высокотемпературных сверхпроводников при высоком давлении: методы и материалы». Physics Reports . 856 : 1–78. arXiv : 1905.06693 . Bibcode :2020PhR...856....1F. doi :10.1016/j.physrep.2020.02.003. S2CID  155100283.
  40. ^ Hirsch, JE; Maple, MB; Marsiglio, F. (2015-07-15). "Классы сверхпроводящих материалов: Введение и обзор". Physica C: Сверхпроводимость и ее применение . Сверхпроводящие материалы: обычные, нетрадиционные и неопределенные. 514 : 1–8. arXiv : 1504.03318 . Bibcode :2015PhyC..514....1H. doi :10.1016/j.physc.2015.03.002. ISSN  0921-4534. S2CID  12895850.
  41. ^ "Классификация сверхпроводников" (PDF) . ЦЕРН .
  42. ^ Ван Камп, Мишель; Франсис, Оливье; Лекок, Томас (2017). «Запись гравитационной истории Бельгии». Eos . 98 . doi : 10.1029/2017eo089743 .
  43. ^ Ван Камп, Мишель; де Вирон, Оливье; Уотлет, Арно; Мёрерс, Бруно; Фрэнсис, Оливье; Кодрон, Корентен (2017). "Геофизика на основе наземных измерений силы тяжести, изменяющейся во времени" (PDF) . Обзоры геофизики . 55 (4): 2017RG000566. Bibcode : 2017RvGeo..55..938V. doi : 10.1002/2017rg000566. ISSN  1944-9208. S2CID  134876430.
  44. ^ Тинкхэм, Майкл (1996). Введение в сверхпроводимость . Минеола, Нью-Йорк: Dover Publications, Inc. стр. 8. ISBN 0486435032.
  45. ^ Дроздов, А.; Еремец, М.; Троян, И.; Ксенофонтов, В. (17 августа 2015 г.). «Обычная сверхпроводимость при 203 кельвинах при высоких давлениях в системе гидрида серы». Nature . 525 (2–3): 73–76. arXiv : 1506.08190 . Bibcode :2015Natur.525...73D. doi :10.1038/nature14964. PMID  11369082. S2CID  4468914.
  46. ^ Тинкхэм, Майкл (1996). Введение в сверхпроводимость . Минеола, Нью-Йорк: Dover Publications, Inc. стр. 16. ISBN 0486435032.
  47. ^ Долечек, Р. Л. (1954). «Адиабатическое намагничивание сверхпроводящей сферы». Physical Review . 96 (1): 25–28. Bibcode : 1954PhRv...96...25D. doi : 10.1103/PhysRev.96.25.
  48. ^ Кляйнерт, Х. (1982). «Версия беспорядка абелевой модели Хиггса и порядок сверхпроводящего фазового перехода» (PDF) . Письмо в Nuovo Cimento . 35 (13): 405–412. doi :10.1007/BF02754760. S2CID  121012850.
  49. ^ Хоув, Дж.; Мо, С.; Судбо, А. (2002). "Вихревые взаимодействия и термически индуцированный переход от сверхпроводимости типа I к сверхпроводимости типа II" (PDF) . Physical Review B . 66 (6): 064524. arXiv : cond-mat/0202215 . Bibcode :2002PhRvB..66f4524H. doi :10.1103/PhysRevB.66.064524. S2CID  13672575.
  50. ^ Ландау, Лев Д.; Лифшиц, Евгений М. (1984). Электродинамика сплошных сред . Курс теоретической физики . Том 8. Оксфорд, Англия: Butterworth-Heinemann. ISBN 978-0-7506-2634-7.
  51. ^ Callaway, David JE (1990). «О замечательной структуре сверхпроводящего промежуточного состояния». Nuclear Physics B. 344 ( 3): 627–645. Bibcode : 1990NuPhB.344..627C. doi : 10.1016/0550-3213(90)90672-Z.
  52. ^ ab Wu, MK; et al. (1987). "Сверхпроводимость при 93 К в новой смешанной фазе Y–Ba–Cu–O Compound System при давлении окружающей среды". Physical Review Letters . 58 (9): 908–910. Bibcode :1987PhRvL..58..908W. doi : 10.1103/PhysRevLett.58.908 . PMID  10035069.
  53. ^ "Введение в жидкий гелий". Отделение криогеники и жидкостей . Центр космических полетов имени Годдарда, НАСА.
  54. ^ "Раздел 4.1 'Воздушная пробка в линии заполнения'". Руководство по криогенной системе сверхпроводящего магнитометра для горных пород . 2G Enterprises. Архивировано из оригинала 6 мая 2009 г. Получено 9 октября 2012 г.
  55. ^ Абрикосов, Алексей А. (8 декабря 2003 г.). «Сверхпроводники II типа и вихревая решетка». Нобелевская лекция .
  56. ↑ Гинграс, Оливье (сентябрь 2021 г.). Нетрадиционная сверхпроводимость рутената стронция: электронные корреляции и связь спин-орбита (на французском языке).Кандидатская диссертация.
  57. ^ Манн, Адам (20 июля 2011 г.). «Высокотемпературная сверхпроводимость в 25: все еще в подвешенном состоянии». Nature . 475 (7356): 280–2. Bibcode :2011Natur.475..280M. doi :10.1038/475280a. PMID  21776057. S2CID  205066154.
  58. ^ Pines, D. (2002), «Модель спиновой флуктуации для высокотемпературной сверхпроводимости: прогресс и перспективы», Симметрия щели и флуктуации в высокотемпературных сверхпроводниках , Серия научных исследований НАТО: B, т. 371, Нью-Йорк: Kluwer Academic, стр. 111–142, doi :10.1007/0-306-47081-0_7, ISBN 978-0-306-45934-4
  59. ^ Монту, П.; Балацкий, А. В. и Пайнс, Д. (1991). «К теории высокотемпературной сверхпроводимости в антиферромагнитно коррелированных купратных оксидах». Physical Review Letters . 67 (24): 3448–3451. Bibcode :1991PhRvL..67.3448M. doi : 10.1103/PhysRevLett.67.3448 . PMID  10044736.
  60. ^ Ян Заанен, Ян Лю, Я Сун К. Шалм (2015). Голографическая дуальность в физике конденсированных сред . Cambridge University Press, Кембридж.
  61. ^ Шиллинг, А.; и др. (1993). «Сверхпроводимость выше 130 К в системе Hg–Ba–Ca–Cu–O». Nature . 363 (6424): 56–58. Bibcode :1993Natur.363...56S. doi :10.1038/363056a0. S2CID  4328716.
  62. ^ Дай, П.; Чакумакос, Британская Колумбия; Солнце, ГФ; Вонг, К.В.; и др. (1995). «Синтез и нейтронографическое исследование сверхпроводника HgBa 2 Ca 2 Cu 3 O 8+δ путем замещения Tl». Физика С. 243 (3–4): 201–206. Бибкод : 1995PhyC..243..201D. дои : 10.1016/0921-4534(94)02461-8.
  63. ^ Такахаши, Хироки; Игава, Кадзуми; Арии, Казунобу; Камихара, Йоичи; и др. (2008). «Сверхпроводимость при 43 К в слоистом соединении на основе железа LaO 1− x F x FeAs». Природа . 453 (7193): 376–378. Бибкод : 2008Natur.453..376T. дои : 10.1038/nature06972. PMID  18432191. S2CID  498756.
  64. ^ Чо, Адриан (2014-10-30). «Открыто второе семейство высокотемпературных сверхпроводников». ScienceNOW Daily News.
  65. ^ Ren, Zhi-An; et al. (2008). "Сверхпроводимость и фазовая диаграмма в оксидах мышьяка на основе железа ReFeAsO1-d (Re = редкоземельный металл) без легирования фтором". EPL . 83 (1): 17002. arXiv : 0804.2582 . Bibcode :2008EL.....8317002R. doi :10.1209/0295-5075/83/17002. S2CID  96240327.
  66. ^ Ли, Иньвэй; Хао, Цзянь; Лю, Ханьюй; Ли, Яньлин; Ма, Яньмин (2014-05-07). «Металлизация и сверхпроводимость плотного сероводорода». Журнал химической физики . 140 (17): 174712. arXiv : 1402.2721 . Bibcode : 2014JChPh.140q4712L. doi : 10.1063/1.4874158. ISSN  0021-9606. PMID  24811660. S2CID  15633660.
  67. ^ Дроздов, А.П.; Еремец, МИ; Троян, ИА; Ксенофонтов, В.; Шилин, СИ (2015). «Обычная сверхпроводимость при 203 кельвинах при высоких давлениях в системе гидрида серы». Nature . 525 (7567): 73–6. arXiv : 1506.08190 . Bibcode :2015Natur.525...73D. doi :10.1038/nature14964. ISSN  0028-0836. PMID  26280333. S2CID  4468914.
  68. ^ ab Wood, Charlie (14 октября 2020 г.). «Впервые достигнута сверхпроводимость при комнатной температуре». Журнал Quanta . Получено 29 октября 2020 г.
  69. ^ Дроздов, АП; Конг, ПП; Миньков В.С.; Беседин, ИП; Кузовников М.А.; Мозаффари, С.; Баликас, Л.; Балакирев Ф.Ф.; Граф, DE; Прокопенко В.Б.; Гринберг, Э.; Князев Д.А.; Ткач, М.; Еремец, МИ (2019). «Сверхпроводимость при 250 К в гидриде лантана под высоким давлением». Природа . 569 (7757): 528–531. arXiv : 1812.01561 . Бибкод : 2019Natur.569..528D. дои : 10.1038/s41586-019-1201-8. PMID  31118520. S2CID  119231000.
  70. ^ Cao, Yuan ; Fatemi, Valla; Demir, Ahmet; Fang, Shiang; Tomarken, Spencer L.; Luo, Jason Y.; Sanchez-Yamagishi, JD; Watanabe, K.; Taniguchi, T. (2018-03-05). "Коррелированное поведение изолятора при половинном заполнении в сверхрешетках графена с магическим углом". Nature . 556 (7699): 80–84. arXiv : 1802.00553 . Bibcode :2018Natur.556...80C. doi :10.1038/nature26154. ISSN  1476-4687. PMID  29512654. S2CID  4601086.
  71. ^ Вуд, Чарли (16 марта 2021 г.). «Новый поворот раскрывает секреты сверхпроводимости». Журнал Quanta . Получено 23.03.2021 .
  72. ^ Снайдер, Элиот и др. (14 октября 2020 г.). «Комнатно-температурная сверхпроводимость в углеродистом гидриде серы». Nature . 586 (7829): 373–377. Bibcode :2020Natur.586..373S. doi :10.1038/s41586-020-2801-z. OSTI  1673473. PMID  33057222. S2CID  222823227.(Отозвано, см. doi :10.1038/s41586-022-05294-9, PMID  36163290)
  73. ^ Чанг, Кеннет (14 октября 2020 г.). «Наконец-то первый сверхпроводник при комнатной температуре». The New York Times .
  74. ^ Снайдер, Эллиот; Дазенброк-Гаммон, Натан; Макбрайд, Рэймонд; Дебессай, Мэтью; Виндана, Хиранья; Венкатасами, Кевин; Лоулер, Кит В.; Саламат, Ашкан; Диас, Ранга П. (26 сентября 2022 г.). «Замечание об отзыве: сверхпроводимость при комнатной температуре в гидриде углеродистой серы». Nature . 610 (7933): 804. Bibcode :2022Natur.610..804S. doi : 10.1038/s41586-022-05294-9 . PMID  36163290. S2CID  252544156.
  75. ^ Копелевич, Яков; Торрес, Хосе; Да Силва, Робсон; Оливейра, Фелипе; Диамантини, Мария Кристина; Тругенбергер, Карло; Винокур, Валерий (2024). "Глобальная сверхпроводимость при комнатной температуре в графите". Advanced Quantum Technologies . 7 (2). arXiv : 2208.00854 . doi :10.1002/qute.202300230.
  76. ^ Надим, Мухаммад; Фюрер, Майкл С.; Ван, Сяолинь (2023). "Эффект сверхпроводящего диода" . Nature Reviews Physics . 5 (10): 558–577. Bibcode : 2023NatRP...5..558N. doi : 10.1038/s42254-023-00632-w. ISSN  2522-5820. S2CID  261976918.
  77. ^ « Проектирование и полевые испытания первого в мире ротора ReBCO для ветрогенератора мощностью 3,6 МВт» Энн Берген, Расмус Андерсен, Маркус Бауэр, Герман Бой, Марсель тер Браке, Патрик Брутсаерт, Карстен Бюрер, Марк Дхалле, Йеспер Хансен и Герман тен Кате, 25 октября 2019 г., Наука и технологии сверхпроводников.
  78. ^ Брок, Дэвид С. (2014-03-19). "Забытый криотронный компьютер Дадли Бака". Институт инженеров по электротехнике и электронике . Получено 2021-03-30 .
  79. ^ Морозов, Дмитрий В.; Касабури, Алессандро; Хэдфилд, Роберт Х. (2022-03-11). "Сверхпроводящие детекторы фотонов" (PDF) . Contemporary Physics . 62 (2): 69–91. doi :10.1080/00107514.2022.2043596. ISSN  0010-7514. S2CID  247422273.
  80. ^ Natarajan, CM (апрель 2012 г.). «Сверхпроводящие нанопроволочные однофотонные детекторы: физика и применение». Superconductor Science and Technology . 25 (6): 063001. arXiv : 1204.5560 . Bibcode : 2012SuScT..25f3001N. doi : 10.1088/0953-2048/25/6/063001. S2CID  4893642 – через IOP Publishing.
  81. ^ Ислам; и др. (2014). «Обзор гондолы офшорной ветровой турбины: технические проблемы, тенденции исследований и разработок». Обзоры возобновляемой и устойчивой энергетики . 33 : 161–176. Bibcode : 2014RSERv..33..161I. doi : 10.1016/j.rser.2014.01.085. hdl : 10453/33256 .
  82. ^ Линдер, Якоб; Робинсон, Джейсон WA (2 апреля 2015 г.). «Сверхпроводящая спинтроника». Nature Physics . 11 (4): 307–315. arXiv : 1510.00713 . Bibcode : 2015NatPh..11..307L. doi : 10.1038/nphys3242. S2CID  31028550.
  83. ^ Томас; и др. (2016). «Сверхпроводящие линии электропередачи – устойчивая передача электроэнергии с более высоким общественным признанием?» (PDF) . Обзоры возобновляемой и устойчивой энергетики . 55 : 59–72. Bibcode :2016RSERv..55...59T. doi : 10.1016/j.rser.2015.10.041 .
  84. ^ Рен, Ли и др. (2009). «Техническая и экономическая оценка кабелей ВТСП». Труды IEEE по прикладной сверхпроводимости . 19 (3): 1774–1777. doi :10.1109/TASC.2009.2019058. S2CID  46117301.
  85. ^ "Все Нобелевские премии по физике". Nobelprize.org . Nobel Media AB 2014.

Дальнейшее чтение

Внешние ссылки

В Викицитатнике есть цитаты, связанные со сверхпроводимостью .