Контроллер замкнутого контура

Контроллер с замкнутым контуром или контроллер с обратной связью — это контур управления , который включает обратную связь , в отличие от контроллера с разомкнутым контуром или контроллера без обратной связи . Контроллер с замкнутым контуром использует обратную связь для управления состояниями или выходами динамической системы . Его название происходит от информационного пути в системе: входы процесса (например, напряжение, подаваемое на электродвигатель ) оказывают влияние на выходы процесса (например, скорость или крутящий момент двигателя), которые измеряются датчиками и обрабатываются контроллером; результат (сигнал управления) «возвращается обратно» в качестве входа в процесс, замыкая контур. ^[1]

В случае линейных систем обратной связи контур управления , включающий датчики , алгоритмы управления и исполнительные механизмы, организован в попытке регулировать переменную в заданном значении (SP). Повседневным примером является круиз-контроль на дорожном транспортном средстве; где внешние воздействия, такие как холмы, могут вызвать изменение скорости, и водитель имеет возможность изменить желаемую заданную скорость. Алгоритм ПИД в контроллере восстанавливает фактическую скорость до желаемой скорости оптимальным образом, с минимальной задержкой или перерегулированием , управляя выходной мощностью двигателя транспортного средства. Системы управления, которые включают некоторое восприятие результатов, которых они пытаются достичь, используют обратную связь и могут в некоторой степени адаптироваться к изменяющимся обстоятельствам. Системы управления с разомкнутым контуром не используют обратную связь и работают только заранее заданными способами.

Контроллеры с замкнутым контуром имеют следующие преимущества по сравнению с контроллерами с разомкнутым контуром:

подавление помех (например, холмов в примере круиз-контроля выше)
гарантированная производительность даже при наличии неопределенностей модели , когда структура модели не полностью соответствует реальному процессу, а параметры модели неточны
нестабильные процессы можно стабилизировать
снижение чувствительности к изменению параметров
улучшенная производительность отслеживания ссылок
улучшенное исправление случайных колебаний ^[2]

В некоторых системах замкнутый и разомкнутый контуры управления используются одновременно. В таких системах разомкнутый контур управления называется прямой связью и служит для дальнейшего улучшения характеристик отслеживания опорных сигналов.

Распространенной архитектурой регулятора замкнутого контура является ПИД-регулятор .

Открытый и закрытый контур

По сути, существует два типа контура управления: управление с разомкнутым контуром (прямая связь) и управление с замкнутым контуром (обратная связь).

Электромеханический таймер, обычно используемый для управления в разомкнутом контуре, основанном исключительно на временной последовательности, без обратной связи от процесса.

При управлении с открытым контуром управляющее воздействие контроллера не зависит от «выходного сигнала процесса» (или «регулируемой переменной процесса»). Хорошим примером этого является котел центрального отопления, управляемый только таймером, так что тепло подается в течение постоянного времени, независимо от температуры здания. Управляющим воздействием является включение/выключение котла, но управляемой переменной должна быть температура здания, но это не так, поскольку это управление котлом с открытым контуром, которое не дает замкнутого контура управления температурой.

В управлении с замкнутым контуром управляющее воздействие контроллера зависит от выходного сигнала процесса. В случае аналогии с котлом это будет включать термостат для контроля температуры здания и, таким образом, обратной связи сигнала, чтобы гарантировать, что контроллер поддерживает температуру здания на уровне, установленном на термостате. Таким образом, контроллер с замкнутым контуром имеет контур обратной связи, который гарантирует, что контроллер применяет управляющее воздействие для выдачи выходного сигнала процесса, соответствующего «опорному входу» или «заданному значению». По этой причине контроллеры с замкнутым контуром также называются контроллерами с обратной связью. ^[3]

Определение замкнутой системы управления согласно Британскому институту стандартов : «система управления, имеющая контрольную обратную связь, причем сигнал отклонения, сформированный в результате этой обратной связи, используется для управления действием конечного элемента управления таким образом, чтобы стремиться свести отклонение к нулю». ^[4]

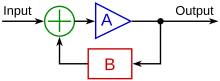
Аналогично; « Система управления с обратной связью — это система, которая стремится поддерживать заданное соотношение одной системной переменной к другой путем сравнения функций этих переменных и использования разницы в качестве средства управления». ^[5]

Передаточная функция замкнутого контура

Выход системы y ( t ) возвращается через измерение датчика F для сравнения с опорным значением r ( t ). Затем контроллер C принимает ошибку e (разницу) между опорным значением и выходом для изменения входов u в системе под управлением P. Это показано на рисунке. Этот тип контроллера является контроллером с замкнутым контуром или контроллером с обратной связью.

Это называется системой управления с одним входом и одним выходом ( SISO ); системы MIMO (т. е. многовходовые и многовыходовые) с более чем одним входом/выходом являются обычным явлением. В таких случаях переменные представляются векторами вместо простых скалярных значений. Для некоторых систем с распределенными параметрами векторы могут быть бесконечномерными ( обычно это функции).

Если предположить, что контроллер C , объект P и датчик F линейны и не зависят от времени (т. е. элементы их передаточной функции C ( s ), P ( s ) и F ( s ) не зависят от времени), то приведенные выше системы можно проанализировать с использованием преобразования Лапласа над переменными. Это дает следующие соотношения:

Y(s)=P(s)U(s)

U(s)=C(s)E(s)

E(s)=R(s)-F(s)Y(s).

Решение для Y ( s ) через R ( s ) дает

Y(s)=\left({\frac {P(s)C(s)}{1+P(s)C(s)F(s)}}\right)R(s)=H(s)R(s).

Выражение называется передаточной функцией замкнутого контура системы. Числитель — это прямой (разомкнутый) коэффициент усиления от r до y , а знаменатель — это единица плюс коэффициент усиления при обходе контура обратной связи, так называемый петлевой коэффициент усиления. Если , т. е. он имеет большую норму при каждом значении s , и если , то Y ( s ) приблизительно равен R ( s ), а выходной сигнал точно соответствует опорному входному сигналу. $H(s)={\frac {P(s)C(s)}{1+F(s)P(s)C(s)}}$ $|P(s)C(s)|\gg 1$ $|F(s)|\approx 1$

ПИД-регулирование с обратной связью

Пропорционально-интегрально-дифференциальный регулятор (ПИД-регулятор) — это метод управления механизмом обратной связи контура управления, широко используемый в системах управления.

Контроллер ПИД непрерывно вычисляет значение ошибки $e (t)$ как разницу между желаемой уставкой и измеренной переменной процесса и применяет коррекцию на основе пропорциональных , интегральных и производных членов. ПИД — это аббревиатура от Proportional-Integral-Derivative , относящаяся к трем членам, работающим с сигналом ошибки для создания управляющего сигнала.

Теоретическое понимание и применение датируется 1920-ми годами, и они реализованы почти во всех аналоговых системах управления; первоначально в механических контроллерах, затем с использованием дискретной электроники и позднее в промышленных компьютерах. ПИД-регулятор, вероятно, является наиболее используемой конструкцией управления с обратной связью.

Если $u (t)$ — управляющий сигнал, отправляемый в систему, $y (t)$ — измеренный выходной сигнал, $r (t)$ — желаемый выходной сигнал, а $e (t) = r (t) - y (t)$ — ошибка отслеживания, то ПИД-регулятор имеет общую форму

u(t)=K_{P}e(t)+K_{I}\int ^{t}e(\tau ){\text{d}}\tau +K_{D}{\frac {{\text{d}}e(t)}{{\text{d}}t}}.

Желаемая динамика замкнутого контура достигается путем регулировки трех параметров $K P$ , $K I$ и $K D$ , часто итеративно путем «настройки» и без специальных знаний о модели установки. Устойчивость часто может быть обеспечена с использованием только пропорционального члена. Интегральный член позволяет отбрасывать ступенчатое возмущение (часто поразительная спецификация в управлении процессом ). Производный член используется для обеспечения демпфирования или формирования отклика. ПИД-регуляторы являются наиболее устоявшимся классом систем управления: однако их нельзя использовать в нескольких более сложных случаях, особенно если рассматриваются системы MIMO .

Применение преобразования Лапласа приводит к преобразованному уравнению ПИД-регулятора

u(s)=K_{P}\,e(s)+K_{I}\,{\frac {1}{s}}\,e(s)+K_{D}\,s\,e(s)

u(s)=\left(K_{P}+K_{I}\,{\frac {1}{s}}+K_{D}\,s\right)e(s)

с передаточной функцией ПИД-регулятора

C(s)=\left(K_{P}+K_{I}\,{\frac {1}{s}}+K_{D}\,s\right).

В качестве примера настройки ПИД-регулятора в замкнутой системе $H (s)$ рассмотрим установку 1-го порядка, заданную формулой

P(s)={\frac {A}{1+sT_{P}}}

где $A$ и $T P$ — некоторые константы. Выход завода возвращается через

F(s)={\frac {1}{1+sT_{F}}}

где $T F$ также является константой. Теперь, если мы установим , $K$ $D$ $=$ $KT$ $D$ , и , мы можем выразить передаточную функцию ПИД-регулятора в последовательной форме как $K_{P}=K\left(1+{\frac {T_{D}}{T_{I}}}\right)$ $K_{I}={\frac {K}{T_{I}}}$

C(s)=K\left(1+{\frac {1}{sT_{I}}}\right)(1+sT_{D})

Подставляя $P (s)$ , $F (s)$ и $C (s)$ в передаточную функцию замкнутого контура $H (s)$ , мы находим, что, установив

K={\frac {1}{A}},T_{I}=T_{F},T_{D}=T_{P}

$H (s) = 1.$ При такой настройке в этом примере выходной сигнал системы точно соответствует опорному входному сигналу.

Однако на практике чистый дифференциатор не является ни физически реализуемым, ни желательным ^[6] из-за усиления шума и резонансных мод в системе. Поэтому вместо него используется подход типа компенсатора с опережением фазы или дифференциатор с низкочастотным спадом.

Ссылки

^ Беххофер, Джон (2005-08-31). «Обратная связь для физиков: учебное эссе по управлению». Обзоры современной физики . 77 (3): 783–836. doi :10.1103/RevModPhys.77.783.
^ Cao, FJ; Feito, M. (2009-04-10). "Термодинамика систем с обратной связью". Physical Review E. 79 ( 4): 041118. arXiv : 0805.4824 . doi :10.1103/PhysRevE.79.041118.
^ "Обратная связь и системы управления" - JJ Di Steffano, AR Stubberud, IJ Williams. Серия набросков Шаумса, McGraw-Hill 1967
^ Майр, Отто (1970). Истоки управления с обратной связью . Клинтон, MA США: The Colonial Press, Inc.
^ Майр, Отто (1969). Истоки управления с обратной связью . Клинтон, MA США: The Colonial Press, Inc.
^ Ang, KH; Chong, GCY; Li, Y. (2005). "Анализ, проектирование и технология систем ПИД-управления" (PDF) . IEEE Transactions on Control Systems Technology . 13 (4): 559–576. doi :10.1109/TCST.2005.847331. S2CID 921620. Архивировано (PDF) из оригинала 2013-12-13.