Комплексный многогранник

В геометрии комплексный многогранник — это обобщение многогранника в реальном пространстве до аналогичной структуры в комплексном гильбертовом пространстве , где каждое действительное измерение сопровождается мнимым .

Сложный многогранник можно понимать как совокупность комплексных точек, линий, плоскостей и т. д., где каждая точка является соединением нескольких прямых, каждая линия нескольких плоскостей и т. д.

Точные определения существуют только для правильных комплексных многогранников, которые являются конфигурациями . Правильные комплексные многогранники полностью охарактеризованы и могут быть описаны с использованием символической записи, разработанной Коксетером .

Также были описаны некоторые сложные многогранники, которые не являются полностью правильными.

Определения и введение

Комплексная линия имеет одно измерение с действительными координатами, а другое с мнимыми координатами. Говорят, что применение реальных координат к обоим измерениям дает им два измерения по сравнению с действительными числами. Реальная плоскость с воображаемой осью, обозначенной как таковая, называется диаграммой Аргана . Из-за этого ее иногда называют комплексной плоскостью. Таким образом, комплексное двумерное пространство (также иногда называемое комплексной плоскостью) представляет собой четырехмерное пространство над реальными объектами и так далее в более высоких измерениях. ${\displaystyle \mathbb {C} ^{1}}$

Комплексный n -многогранник в комплексном n -пространстве является аналогом вещественного n - многогранника в реальном n -пространстве. Однако не существует естественного комплексного аналога упорядочения точек на прямой (или связанных с ним комбинаторных свойств). Из-за этого сложный многогранник нельзя рассматривать как непрерывную поверхность и он не ограничивает внутреннюю часть, как это делает настоящий многогранник.

В случае правильных многогранников точное определение можно дать, используя понятие симметрии. Для любого правильного многогранника группа симметрии (здесь комплексная группа отражений , называемая группой Шепарда ) действует транзитивно на флагах , то есть на вложенных последовательностях точек, содержащихся в прямой, содержащейся в плоскости, и так далее.

Более полно, скажем, что набор P аффинных подпространств (или квартир ) комплексного унитарного пространства V размерности n является правильным комплексным многогранником, если он удовлетворяет следующим условиям: ^{[1] [2]}

• для каждого −1 ⩽ i < j < k ⩽ n , если F — квартира в P размерности i , а H — квартира в P размерности k такая, что F ⊂ H , то существует по крайней мере две квартиры G в P размерности j такой, что F ⊂ G ⊂ H ;
• для каждого i , j такого, что −1 ⩽ i < j − 2, j ⩽ n , если F ⊂ G — квартиры P размеров i , j , то множество квартир между F и G связно в том смысле, что можно перейти от любого члена этого множества к любому другому с помощью последовательности вложений; и
• подмножество унитарных преобразований V , фиксирующих P , транзитивно на флагах F ₀ ⊂ F ₁ ⊂ … ⊂ F _n квартир P (причем Fi размерности _i для всех i ).

(Здесь под плоскостью размерности −1 понимается пустое множество.) Таким образом, по определению правильные комплексные многогранники представляют собой конфигурации в комплексном унитарном пространстве.

Правильные комплексные многогранники были открыты Шепардом (1952), а теория получила дальнейшее развитие Коксетером (1974).

Комплексный многогранник существует в комплексном пространстве эквивалентной размерности. Например, вершины комплексного многоугольника — это точки комплексной плоскости (плоскость, в которой каждая точка имеет в качестве координат два комплексных числа, не путать с плоскостью Аргана комплексных чисел), а ребра — это комплексные линии, существующие как (аффинные) подпространства плоскости и пересекающиеся в вершинах. Таким образом, как одномерное комплексное пространство, ребру может быть присвоена собственная система координат, в которой каждая точка ребра представлена ​​одним комплексным числом. ${\displaystyle \mathbb {C} ^{2}}$ ${\displaystyle \mathbb {C} ^{1}}$

В правильном комплексном многограннике вершины, инцидентные ребру, расположены симметрично относительно их центроида , который часто используется в качестве начала системы координат ребра (в реальном случае центроид — это всего лишь середина ребра). Симметрия возникает из-за сложного отражения центроида; это отражение оставит величину любой вершины неизменной, но изменит ее аргумент на фиксированную величину, переместив его к координатам следующей по порядку вершины. Таким образом, мы можем предположить (после подходящего выбора масштаба), что вершины на ребре удовлетворяют уравнению, где p — количество инцидентных вершин. Таким образом, в диаграмме Аргана ребра точки вершин лежат в вершинах правильного многоугольника с центром в начале координат. ${\displaystyle x^{p}-1=0}$

Выше показаны три действительные проекции правильного комплексного многоугольника 4{4}2 с ребрами a, b, c, d, e, f, g, h . Он имеет 16 вершин, которые для ясности не отмечены индивидуально. Каждое ребро имеет четыре вершины, и каждая вершина лежит на двух ребрах, следовательно, каждое ребро пересекается с четырьмя другими ребрами. На первой диаграмме каждое ребро представлено квадратом. Стороны квадрата не являются частями многоугольника, а нарисованы исключительно для того, чтобы визуально связать четыре вершины. Края выкладываются симметрично. (Обратите внимание, что диаграмма похожа на проекцию тессеракта на плоскость Кокстера B 4 , но структурно отличается).

Средняя диаграмма отказывается от восьмиугольной симметрии в пользу ясности. Каждое ребро отображается как реальная линия, а каждая точка пересечения двух линий является вершиной. Связь между различными краями очевидна.

Последняя диаграмма дает представление о структуре, проецируемой в трех измерениях: два куба с вершинами на самом деле имеют одинаковый размер, но видны в перспективе на разных расстояниях в четвертом измерении.

Регулярные комплексные одномерные многогранники

Комплексные 1-многогранники, представленные на плоскости Аргана в виде правильных многоугольников для p = 2, 3, 4, 5 и 6, с черными вершинами. Центр тяжести вершин p показан красным. Стороны многоугольников представляют собой одно применение генератора симметрии, сопоставляющее каждую вершину со следующей копией, расположенной против часовой стрелки. Эти многоугольные стороны не являются реберными элементами многогранника, поскольку комплексный 1-многогранник не может иметь ребер (часто это комплексное ребро) и содержит только вершинные элементы.

Реальный одномерный многогранник существует как замкнутый сегмент вещественной линии , определяемый двумя его конечными точками или вершинами на линии. Его символ Шлефли — {} . ${\displaystyle \mathbb {R} ^{1}}$

Аналогично, комплексный 1-многогранник существует как набор p вершинных точек комплексной прямой . Их можно представить как набор точек на диаграмме Аргана ( x , y )= x + iy . Правильный комплексный одномерный многогранник _p {} имеет p ( p ≥ 2) точек вершин, расположенных так, чтобы образовывать выпуклый правильный многоугольник { p } на плоскости Аргана. ^[4] ${\displaystyle \mathbb {C} ^{1}}$

В отличие от точек реальной линии, точки комплексной линии не имеют естественного порядка. Таким образом, в отличие от реальных многогранников, внутренняя часть не может быть определена. ^[5] Несмотря на это, комплексные 1-многогранники часто изображают, как здесь, в виде ограниченного правильного многоугольника в плоскости Аргана.

Реальный край создается как линия между точкой и ее отражением в зеркале. Унитарный порядок отражения 2 можно рассматривать как поворот на 180 градусов вокруг центра. Край неактивен , если точка генератора находится на отражающей линии или в центре.

Правильный вещественный одномерный многогранник представляется пустым символом Шлефли {} или диаграммой Коксетера-Динкина. . Точка или узел диаграммы Кокстера-Динкина сама по себе представляет генератор отражения, а круг вокруг узла означает, что точка генератора не находится в отражении, поэтому ее отражающее изображение является отдельной точкой от самой себя. В более широком смысле, правильный комплексный одномерный многогранник в имеет диаграмму Кокстера-Дынкина. ${\displaystyle \mathbb {C} ^{1}}$ , для любого положительного целого числа p , 2 или больше, содержащего p вершин. p может быть подавлен, если он равен 2. Он также может быть представлен пустым символом Шлефли _p {}, } _p {, {} _p или _p {2} ₁ . 1 — это обозначение-заполнитель, представляющее несуществующее отражение или генератор идентификаторов периода 1. (0-многогранник, действительный или комплексный, является точкой и представлен как } { или ₁ {2} ₁ .)

Симметрия обозначается диаграммой Кокстера. , и альтернативно может быть описан в нотации Кокстера как _p [], [] _p или ] _p [, _p [2] ₁ или _p [1] _p . Симметрия изоморфна циклической группе порядка p . ^[6] Подгруппами _p [] являются любые целые дивизоры d , _d [], где d ≥2.

Генератор унитарного оператора длярассматривается как вращение на 2π/ p радиан против часовой стрелки , акрай создается последовательным применением одного унитарного отражения. Генератор унитарного отражения для 1-многогранника с p вершинами — это e ^{2π i / p} = cos(2π/ p ) + i sin(2π/ p ) . При p = 2 генератором является e ^{π i} = –1, то же, что и точечное отражение в реальной плоскости.

В более сложных многогранниках 1-многогранники образуют p -ребра. 2-ребро похоже на обычное вещественное ребро тем, что оно содержит две вершины, но не обязательно должно находиться на реальной линии.

Правильные сложные многоугольники

В то время как 1-многогранники могут иметь неограниченное количество p , конечные правильные комплексные многоугольники, за исключением многоугольников двойной призмы _p {4} ₂ , ограничены элементами с 5 ребрами (пятиугольными ребрами), а бесконечные правильные апейрогоны также включают 6 ребер (шестиугольные ребра). элементы.

Обозначения

Модифицированная нотация Шепарда Шлефли

Первоначально Шепард разработал модифицированную форму обозначения Шлефли для правильных многогранников. Для многоугольника, ограниченного p ₁ -ребрами, с p ₂ -множеством в качестве вершины и общей группой симметрии порядка g , мы обозначаем многоугольник как p ₁ ( g ) p ₂ .

Тогда количество вершин V равно g / p ₂ , а количество ребер E равно g / p ₁ .

Сложный многоугольник, показанный выше, имеет восемь квадратных ребер ( p ₁ =4) и шестнадцать вершин ( p ₂ =2). Отсюда мы можем определить, что g = 32, что дает модифицированный символ Шлефли 4(32)2.

Пересмотренная модифицированная нотация Шлефли Коксетера

Более современное обозначение _{p 1} { q } _{p 2} принадлежит Кокстеру [ ^7] и основано на теории групп. Как группа симметрии, ее символ — _{p 1} [ q ] _{p 2} .

Группа симметрии _{p 1} [ q ] _{p 2} представлена ​​2 образующими R ₁ , R ₂ , где: R ₁ ^{p ₁} = R ₂ ^{p ₂} = I. Если q четно, (R ₂ R ₁ ) ^{q /2} = (Р ₁ Р ₂ ) ^{q /2} . Если q нечетно, (R ₂ R ₁ ) ^(q−1)/2 R ₂ = (R ₁ R ₂ ) ^{( q −1)/2} R ₁ . Когда q нечетно , p1 = p2 _.​

Для ₄ [4] ₂ имеет R ₁ ⁴ = R ₂ ² = I, (R ₂ R ₁ ) ² = (R ₁ R ₂ ) ² .

Для ₃ [5] ₃ имеет R ₁ ³ = R ₂ ³ = I, (R ₂ R ₁ ) ² R ₂ = (R ₁ R ₂ ) ² R ₁ .

Диаграммы Кокстера-Динкина

Коксетер также обобщил использование диаграмм Кокстера-Динкина на сложные многогранники, например, комплексный многоугольник _p { q } _r представлен формулойи эквивалентная группа симметрии _p [ q ] _r представляет собой диаграмму без колец.. Узлы p и r представляют собой зеркала, создающие изображения p и r в плоскости. Непомеченные узлы на диаграмме имеют две неявные метки. Например, настоящий правильный многоугольник — это ₂ { q } ₂ или { q } или.

Одно ограничение: узлы, соединенные нечетными порядками ветвей, должны иметь одинаковые порядки узлов. Если этого не сделать, группа создаст «звездные» полигоны с перекрывающимися элементами. Такиявляются обычными, в то время какзвездный.

12 неприводимых групп Шепарда

12 неприводимых групп Шепарда с отношениями индексов их подгрупп. ^[8] Подгруппы с индексом 2 связываются путем удаления реального отражения:
_p [2 q ] ₂ → _p [ q ] _p , индекс 2.
_p [4] _q → _p [ q ] _p , индекс q .

_p [4] ₂ подгруппы: p=2,3,4...
_p [4] ₂ → [ p ], индекс p
_p [4] ₂ → _p []× _p [], индекс 2

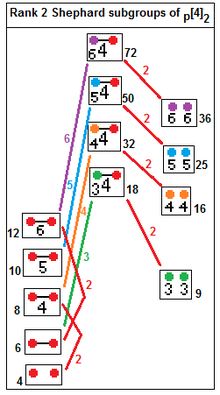
Коксетер перечислил этот список правильных комплексных многоугольников в формате . Правильный комплексный многоугольник, _p { q } _r или ${\displaystyle \mathbb {C} ^{2}}$, имеет p -ребра и r -угольные вершинные фигуры . _p { q } _r — конечный многогранник, если ( p + r ) q > pr ( q -2).

Ее симметрия записывается как _p [ q ] _r , называемая группой Шепарда , аналогичной группе Кокстера , но также допускающей унитарные отражения .

Для незвездных групп порядок группы _p [ q ] _r можно вычислить как . ^[9] ${\displaystyle g=8/q\cdot (1/p+2/q+1/r-1)^{-2}}$

Число Кокстера для _p [ q ] _r равно , поэтому порядок группы также можно вычислить как . Правильный комплексный многоугольник можно нарисовать в ортогональной проекции с h -угольной симметрией. ${\displaystyle h=2/(1/p+2/q+1/r-1)}$ ${\displaystyle g=2h^{2}/q}$

Решения ранга 2, которые генерируют сложные многоугольники:

Исключенные решения с нечетным q и неравными p и r : ₆ [3] ₂ , ₆ [3] ₃ , ₉ [3] ₃ , ₁₂ [3] ₃ , ..., ₅ [5] ₂ , ₆ [5] ₂ , ₈ [5] ₂ , ₉ [5] ₂ , ₄ [7] ₂ , ₉ [5] ₂ , ₃ [9] ₂ и ₃ [11] ₂ .

Другие целые q с неравными p и r создают звездные группы с перекрывающимися фундаментальными областями:,,,,, и.

Двойной многоугольник _p { q } _r — это _r { q } _p . Многоугольник вида _p { q } _p самодвойственный. Группы вида _p [2 q ] ₂ обладают полусимметрией _p [ q ] _p , поэтому правильный многоугольникто же самое, что и квазирегулярный. А также правильный многоугольник с тем же порядком узлов,, имеют альтернативную конструкцию, что позволяет смежным краям иметь два разных цвета. ^[10]

Порядок группы g используется для вычисления общего количества вершин и ребер. Он будет иметь вершины g / r и ребра g / p . Когда p = r , количество вершин и ребер одинаково. Это условие требуется, когда q нечетно.

Матричные генераторы

Группа p [ q ] r ,, можно представить двумя матрицами: ^[11]

С

к= ${\displaystyle {\sqrt {\frac {cos({\frac {\pi }{p}}-{\frac {\pi }{r}})+cos({\frac {2\pi }{q}})}{2\sin {\frac {\pi }{p}}\sin {\frac {\pi }{r}}}}}}$

Примеры

Перечисление правильных комплексных многоугольников

Коксетер перечислил комплексные многоугольники в Таблице III Правильных комплексных многогранников. ^[12]

Визуализации правильных сложных многоугольников

Многоугольники формы _p {2 r } _q можно визуализировать с помощью q наборов цветов p -ребра. Каждое p -ребро рассматривается как правильный многоугольник, при этом грани отсутствуют.

2D ортогональные проекции комплексных многоугольников ₂ { r } _q

Многоугольники вида ₂ {4} _q называются обобщенными ортоплексами . Они имеют общие вершины с 4D - дуопирамидами q - q , вершины которых соединены 2-ребрами.

• 
  ₂ {4} ₂ ,, с 4 вершинами и 4 ребрами
• 
  ₂ {4} ₃ ,, с 6 вершинами и 9 ребрами ^[13]
• 
  ₂ {4} ₄ ,, с 8 вершинами и 16 ребрами
• 
  ₂ {4} ₅ ,, с 10 вершинами и 25 ребрами
• 
  ₂ {4} ₆ ,, с 12 вершинами и 36 ребрами
• 
  ₂ {4} ₇ ,, с 14 вершинами и 49 ребрами
• 
  ₂ {4} ₈ ,, с 16 вершинами и 64 ребрами
• 
  ₂ {4} ₉ ,, с 18 вершинами и 81 ребром
• 
  ₂ {4} ₁₀ ,, с 20 вершинами и 100 ребрами

Комплексные многоугольники _p {4} ₂

Многоугольники вида _p {4} ₂ называются обобщенными гиперкубами (квадратами для многоугольников). Они имеют общие вершины с 4D дуопризмами p - p , вершины которых соединены p-ребрами. Вершины рисуются зеленым цветом, а p -ребра — чередующимися цветами: красным и синим. Перспектива немного искажается для нечетных размеров, чтобы переместить перекрывающиеся вершины из центра.

• 
  ₂ {4} ₂ ,или, с 4 вершинами и 4 2-ребрами
• 
  ₃ {4} ₂ ,или, с 9 вершинами и 6 (треугольными) 3-ребрами ^[13]
• 
  ₄ {4} ₂ ,или, с 16 вершинами и 8 (квадратными) 4-ребрами
• 
  ₅ {4} ₂ ,или, с 25 вершинами и 10 (пятиугольными) 5-ребрами
• 
  ₆ {4} ₂ ,или, с 36 вершинами и 12 (шестиугольными) 6-ребрами
• 
  ₇ {4} ₂ ,или, с 49 вершинами и 14 (семиугольными)7-ребрами
• 
  ₈ {4} ₂ ,или, с 64 вершинами и 16 (восьмиугольными) 8-ребрами
• 
  ₉ {4} ₂ ,или, с 81 вершиной и 18 (эннеагональными) 9-ребрами
• 
  ₁₀ {4} ₂ ,или, со 100 вершинами и 20 (десятиугольными) 10-ребрами

3D перспективные проекции сложных многоугольников _p {4} ₂ . Двойники ₂ {4} _p

видны путем добавления вершин внутри ребер и добавления ребер вместо вершин.

• 
  ₃ {4} ₂ , илис 9 вершинами, 6 3-ребрами в 2 наборах цветов
• 
  ₂ {4} ₃ ,с 6 вершинами, 9 ребрами в 3 наборах
• 
  ₄ {4} ₂ ,илис 16 вершинами, 8 4-ребрами в 2 наборах цветов и заполненными квадратными 4-ребрами
• 
  ₅ {4} ₂ ,илис 25 вершинами, 10 5-ребрами в 2 наборах цветов

Другие сложные многоугольники _p { r } ₂

• 
  ₃ {6} ₂ ,или, с 24 вершинами черного цвета и 16 3-ребрами, окрашенными в 2 набора 3-ребер красного и синего цвета ^[14]
• 
  ₃ {8} ₂ ,или, с 72 вершинами черного цвета и 48 3-ребрами, окрашенными в 2 набора 3-ребер красного и синего цветов ^[15]

2D ортогональные проекции комплексных многоугольников, _p { r } _p

Многоугольники вида _p { r } _p имеют одинаковое количество вершин и ребер. Они также самодвойственны.

• 
  ₃ {3} ₃ ,или, с 8 вершинами черного цвета и 8 3-ребрами, окрашенными в 2 набора 3-ребер красного и синего цвета ^[16]
• 
  ₃ {4} ₃ ,или, с 24 вершинами и 24 3-ребрами, показанными в 3 наборах цветов, один набор закрашен ^[17]
• 
  ₄ {3} ₄ ,или, с 24 вершинами и 24 4-ребрами, показанными в 4 наборах цветов ^[17]
• 
  ₃ {5} ₃ ,или, со 120 вершинами и 120 3-ребрами ^[18]
• 
  ₅ {3} ₅ ,или, со 120 вершинами и 120 5-ребрами ^[19]

Регулярные комплексные многогранники

В общем, правильный комплексный многогранник представляется Кокстером как _p { z ₁ } _q {z ₂ } _r {z ₃ } _s … или диаграмма Кокстера…, обладающие симметрией _p [ z ₁ ] _q [ z ₂ ] _r [ z ₃ ] _s … или…. ^[20]

Существуют бесконечные семейства правильных комплексных многогранников, которые встречаются во всех измерениях, обобщая гиперкубы и перекрестные многогранники в реальном пространстве. «Обобщенный ортотоп» Шепарда обобщает гиперкуб; у него есть символ, заданный γ^п
_н= _р {4} ₂ {3} ₂ … ₂ {3} ₂ и диаграмма…. Его группа симметрии имеет диаграмму _p [4] ₂ [3] ₂ … ₂ [3] ₂ ; в классификации Шепарда-Тодда это группа G( p , 1, n ), обобщающая знаковые матрицы перестановок. Его двойственный правильный многогранник, «обобщенный перекрестный многогранник», обозначается символом β.^п
_н= ₂ {3} ₂ {3} ₂ … ₂ {4} _п и схема…. ^[21]

Одномерный правильный комплексный многогранник в представлен в виде ${\displaystyle \mathbb {C} ^{1}}$, имеющий p вершин, с его действительным представлением в виде правильного многоугольника { p }. Коксетер также дает ему символ γ.^п
₁или β^п
₁как одномерный обобщенный гиперкуб или перекрестный многогранник. Его симметрия равна _p [] или, циклическая группа порядка p . В более высоком многограннике _p {} илипредставляет элемент p- ребра с 2-краем, {} или, представляющий обычное вещественное ребро между двумя вершинами. ^[21]

Двойственный комплексный многогранник строится путем замены k и ( n -1- k )-элементов n -многогранника. Например, двойственный комплексный многоугольник имеет вершины, центрированные по каждому краю, а новые ребра центрируются по старым вершинам. Вершина v -валентности создает новое v -ребро, а e -ребра становятся вершинами e -валентности. ^[22] Двойственный правильному комплексному многограннику имеет перевернутый символ. Правильные комплексные многогранники с симметричными символами, т.е. _p { q } _p , _p { q } _r { q } _p , _p { q } _r { s } _r { q } _p и т. д. являются самодвойственными .

Перечисление правильных комплексных многогранников

Некоторые группы Шепарда 3-го ранга с их групповым порядком и рефлексивными отношениями подгрупп.

Коксетер перечислил этот список незвездных правильных комплексных многогранников в , включая 5 платоновых тел в . ^[23] ${\displaystyle \mathbb {C} ^{3}}$ ${\displaystyle \mathbb {R} ^{3}}$

Правильный комплексный многогранник, _p { n ₁ } _q { n ₂ } _r или, имеетлица,края, и вершинные фигуры .

Комплексный правильный многогранник _p { n ₁ } _q { n ₂ } _r требует, чтобы g ₁ = order( _p [ n ₁ ] _q ) и g ₂ = order( _q [ n ₂ ] _r ) были конечными.

Учитывая g = order( _p [ n ₁ ] _q [ n ₂ ] _r ), количество вершин равно g / g ₂ , а количество граней равно g / g ₁ . Число ребер равно g / pr .

Визуализации правильных комплексных многогранников

2D ортогональные проекции комплексных многогранников, _p { s } _t { r } _r

• 
  Реальный {3,3} ,илиимеет 4 вершины, 6 ребер и 4 грани
• 
  ₃ {3} ₃ {3} ₃ ,или, имеет 27 вершин, 72 трёхребра и 27 граней, одна грань выделена синим цветом. ^[25]
• 
  ₂ {4} ₃ {3} ₃ ,имеет 54 вершины, 216 простых ребер и 72 грани, одна грань выделена синим цветом. ^[26]
• 
  ₃ {3} ₃ {4} ₂ ,или, имеет 72 вершины, 216 трёхрёбер и 54 вершины, одна грань выделена синим цветом. ^[27]

Обобщенные октаэдры

Обобщенные октаэдры имеют правильную конструкцию:и квазирегулярную форму как. Все элементы являются симплексами .

• 
  Реальный {3,4} ,или, с 6 вершинами, 12 ребрами и 8 гранями
• 
  ₂ {3} ₂ {4} ₃ ,или, с 9 вершинами, 27 ребрами и 27 гранями
• 
  ₂ {3} ₂ {4} ₄ ,или, с 12 вершинами, 48 ребрами и 64 гранями.
• 
  ₂ {3} ₂ {4} ₅ ,или, с 15 вершинами, 75 ребрами и 125 гранями.
• 
  ₂ {3} ₂ {4} ₆ ,или, с 18 вершинами, 108 ребрами и 216 гранями.
• 
  ₂ {3} ₂ {4} ₇ ,или, с 21 вершиной, 147 ребрами и 343 гранями.
• 
  ₂ {3} ₂ {4} ₈ ,или, с 24 вершинами, 192 ребрами и 512 гранями.
• 
  ₂ {3} ₂ {4} ₉ ,или, с 27 вершинами, 243 ребрами и 729 гранями.
• 
  ₂ {3} ₂ {4} ₁₀ ,или, с 30 вершинами, 300 ребрами и 1000 гранями.

Обобщенные кубы

Обобщенные кубы имеют правильную конструкцию:и призматическая конструкция, как, произведение трех p -угольных 1-многогранников. Элементы представляют собой обобщенные кубы меньшей размерности.

• 
  Действительный {4,3} ,илиимеет 8 вершин, 12 ребер и 6 граней
• 
  ₃ {4} ₂ {3} ₂ ,илиимеет 27 вершин, 27 3-ребер и 9 граней ^[25]
• 
  ₄ {4} ₂ {3} ₂ ,или, с 64 вершинами, 48 ребрами и 12 гранями.
• 
  ₅ {4} ₂ {3} ₂ ,или, со 125 вершинами, 75 ребрами и 15 гранями.
• 
  ₆ {4} ₂ {3} ₂ ,или, с 216 вершинами, 108 ребрами и 18 гранями.
• 
  ₇ {4} ₂ {3} ₂ ,или, с 343 вершинами, 147 ребрами и 21 гранью.
• 
  ₈ {4} ₂ {3} ₂ ,или, с 512 вершинами, 192 ребрами и 24 гранями.
• 
  ₉ {4} ₂ {3} ₂ ,или, с 729 вершинами, 243 ребрами и 27 гранями.
• 
  ₁₀ {4} ₂ {3} ₂ ,или, с 1000 вершинами, 300 ребрами и 30 гранями

Перечисление правильных комплексных 4-многогранников

Коксетер перечислил этот список незвездных правильных комплексных 4-многогранников в , включая 6 выпуклых правильных 4-многогранников в . ^[23] ${\displaystyle \mathbb {C} ^{4}}$ ${\displaystyle \mathbb {R} ^{4}}$

Визуализации правильных комплексных 4-многогранников

• 
  Действительное {3,3,3} ,, имел 5 вершин, 10 ребер, 10 граней {3} и 5 ячеек {3,3}
• 
  Действительное {3,4,3} ,, имел 24 вершины, 96 ребер, 96 граней {3} и 24 ячейки {3,4}.
• 
  Действительное {5,3,3} ,, имел 600 вершин, 1200 ребер, 720 граней {5} и 120 ячеек {5,3}.
• 
  Действительное {3,3,5} ,, имел 120 вершин, 720 ребер, 1200 граней {3} и 600 ячеек {3,3}.
• 
  Соображая многогранник ,, имеет 240 вершин, 2160 3-ребер, 2160 3{3}3 грани и 240 3{3}3{3}3 ячеек.

Обобщенные 4-ортоплексы

Обобщенные 4-ортоплексы имеют правильную конструкцию:и квазирегулярную форму как. Все элементы являются симплексами .

• 
  Действительное {3,3,4} ,или, с 8 вершинами, 24 ребрами, 32 гранями и 16 ячейками
• 
  ₂ {3} ₂ {3} ₂ {4} ₃ ,или, с 12 вершинами, 54 ребрами, 108 гранями и 81 ячейкой.
• 
  ₂ {3} ₂ {3} ₂ {4} ₄ ,или, с 16 вершинами, 96 ребрами, 256 гранями и 256 ячейками.
• 
  ₂ {3} ₂ {3} ₂ {4} ₅ ,или, с 20 вершинами, 150 ребрами, 500 гранями и 625 ячейками.
• 
  ₂ {3} ₂ {3} ₂ {4} ₆ ,или, с 24 вершинами, 216 ребрами, 864 гранями и 1296 ячейками.
• 
  ₂ {3} ₂ {3} ₂ {4} ₇ ,или, с 28 вершинами, 294 ребрами, 1372 гранями и 2401 ячейкой.
• 
  ₂ {3} ₂ {3} ₂ {4} ₈ ,или, с 32 вершинами, 384 ребрами, 2048 гранями и 4096 ячейками.
• 
  ₂ {3} ₂ {3} ₂ {4} ₉ ,или, с 36 вершинами, 486 ребрами, 2916 гранями и 6561 ячейкой.
• 
  ₂ {3} ₂ {3} ₂ {4} ₁₀ ,или, с 40 вершинами, 600 ребрами, 4000 гранями и 10000 ячейками.

Обобщенные 4-кубы

Обобщенные тессеракты имеют правильную конструкцию:и призматическая конструкция, как, произведение четырех p -угольных 1-многогранников. Элементы представляют собой обобщенные кубы меньшей размерности.

• 
  Действительное {4,3,3} ,или, с 16 вершинами, 32 ребрами, 24 гранями и 8 ячейками
• 
  ₃ {4} ₂ {3} ₂ {3} ₂ ,или, с 81 вершиной, 108 ребрами, 54 гранями и 12 ячейками.
• 
  ₄ {4} ₂ {3} ₂ {3} ₂ ,или, с 256 вершинами, 96 ребрами, 96 гранями и 16 ячейками.
• 
  ₅ {4} ₂ {3} ₂ {3} ₂ ,или, с 625 вершинами, 500 ребрами, 150 гранями и 20 ячейками.
• 
  ₆ {4} ₂ {3} ₂ {3} ₂ ,или, с 1296 вершинами, 864 ребрами, 216 гранями и 24 ячейками.
• 
  ₇ {4} ₂ {3} ₂ {3} ₂ ,или, с 2401 вершиной, 1372 ребрами, 294 гранями и 28 ячейками.
• 
  ₈ {4} ₂ {3} ₂ {3} ₂ ,или, с 4096 вершинами, 2048 ребрами, 384 гранями и 32 ячейками.
• 
  ₉ {4} ₂ {3} ₂ {3} ₂ ,или, с 6561 вершиной, 2916 ребрами, 486 гранями и 36 ячейками.
• 
  ₁₀ {4} ₂ {3} ₂ {3} ₂ ,или, с 10000 вершинами, 4000 ребрами, 600 гранями и 40 ячейками.

Перечисление правильных комплексных 5-многогранников

Регулярные комплексные 5-многогранники в или выше существуют в трех семействах: действительные симплексы , обобщенный гиперкуб и ортоплекс . ${\displaystyle \mathbb {C} ^{5}}$

Визуализации правильных комплексных 5-многогранников

Обобщенные 5-ортоплексы

Обобщенные 5-ортоплексы имеют правильную конструкцию:и квазирегулярную форму как. Все элементы являются симплексами .

• 
  Действительное {3,3,3,4} ,, с 10 вершинами, 40 ребрами, 80 гранями, 80 ячейками и 32 4-гранями
• 
  ₂ {3} ₂ {3} ₂ {3} ₂ {4} ₃ ,, с 15 вершинами, 90 ребрами, 270 гранями, 405 ячейками и 243 4-гранями.
• 
  ₂ {3} ₂ {3} ₂ {3} ₂ {4} ₄ ,, с 20 вершинами, 160 ребрами, 640 гранями, 1280 ячейками и 1024 4-гранями.
• 
  ₂ {3} ₂ {3} ₂ {3} ₂ {4} ₅ ,, с 25 вершинами, 250 ребрами, 1250 гранями, 3125 ячейками и 3125 4-гранями.
• 
  ₂ {3} ₂ {3} ₂ {3} ₂ {4} ₆ ,, с 30 вершинами, 360 ребрами, 2160 гранями, 6480 ячейками, 7776 4-гранями
• 
  ₂ {3} ₂ {3} ₂ {3} ₂ {4} ₇ ,, с 35 вершинами, 490 ребрами, 3430 гранями, 12005 ячеек, 16807 4-гранями
• 
  ₂ {3} ₂ {3} ₂ {3} ₂ {4} ₈ ,, с 40 вершинами, 640 ребрами, 5120 гранями, 20480 ячейками, 32768 4-гранями
• 
  ₂ {3} ₂ {3} ₂ {3} ₂ {4} ₉ ,, с 45 вершинами, 810 ребрами, 7290 гранями, 32805 ячейками, 59049 4-гранями
• 
  ₂ {3} ₂ {3} ₂ {3} ₂ {4} ₁₀ ,, с 50 вершинами, 1000 ребрами, 10000 гранями, 50000 ячейками, 100000 4-гранями

Обобщенные 5-кубы

Обобщенные 5-кубы имеют правильную конструкцию:и призматическая конструкция, как, произведение пяти p -угольных 1-многогранников. Элементы представляют собой обобщенные кубы меньшей размерности.

• 
  Действительное {4,3,3,3} ,, с 32 вершинами, 80 ребрами, 80 гранями, 40 ячейками и 10 4-гранями.
• 
  ₃ {4} ₂ {3} ₂ {3} ₂ {3} ₂ ,, с 243 вершинами, 405 ребрами, 270 гранями, 90 ячейками и 15 4-гранями.
• 
  ₄ {4} ₂ {3} ₂ {3} ₂ {3} ₂ ,, с 1024 вершинами, 1280 ребрами, 640 гранями, 160 ячейками и 20 4-гранями.
• 
  ₅ {4} ₂ {3} ₂ {3} ₂ {3} ₂ ,, с 3125 вершинами, 3125 ребрами, 1250 гранями, 250 ячейками и 25 4-гранями.
• 
  ₆ {4} ₂ {3} ₂ {3} ₂ {3} ₂ ,, с 7776 вершинами, 6480 ребрами, 2160 гранями, 360 ячейками и 30 4-гранями.

Перечисление правильных комплексных 6-многогранников

Визуализации правильных комплексных 6-многогранников

Обобщенные 6-ортоплексы

Обобщенные 6-ортоплексы имеют правильную конструкцию:и квазирегулярную форму как. Все элементы являются симплексами .

• 
  Действительное {3,3,3,3,4} ,, с 12 вершинами, 60 ребрами, 160 гранями, 240 ячейками, 192 4-гранями и 64 5-гранями.
• 
  ₂ {3} ₂ {3} ₂ {3} ₂ {3} ₂ {4} ₃ ,, с 18 вершинами, 135 ребрами, 540 гранями, 1215 ячейками, 1458 4-гранями и 729 5-гранями.
• 
  ₂ {3} ₂ {3} ₂ {3} ₂ {3} ₂ {4} ₄ ,, с 24 вершинами, 240 ребрами, 1280 гранями, 3840 ячейками, 6144 4-гранями и 4096 5-гранями.
• 
  ₂ {3} ₂ {3} ₂ {3} ₂ {3} ₂ {4} ₅ ,, с 30 вершинами, 375 ребрами, 2500 гранями, 9375 ячейками, 18750 4-гранями и 15625 5-гранями.
• 
  ₂ {3} ₂ {3} _{2 {3}} 2 {3} ₂ {4} ₆ ,, с 36 вершинами, 540 ребрами, 4320 гранями, 19 440 ячейками, 46 656 4-гранями и 46 656 5-гранями.
• 
  ₂ {3} ₂ {3} ₂ {3} ₂ {3} ₂ {4} ₇ ,, с 42 вершинами, 735 ребрами, 6860 гранями, 36015 ячейками, 100842 4-гранниками, 117649 5-гранниками
• 
  ₂ {3} ₂ {3} ₂ {3} ₂ {3} ₂ {4} ₈ ,, с 48 вершинами, 960 ребрами, 10240 гранями, 61440 ячейками, 196608 4-гранниками, 262144 5-гранниками
• 
  ₂ {3} ₂ {3} _{2 {3}} 2 {3} ₂ {4} ₉ ,, с 54 вершинами, 1215 ребрами, 14580 гранями, 98415 ячейками, 354294 4-гранями, 531441 5-гранями
• 
  ₂ {3} ₂ {3} ₂ {3} ₂ {3} ₂ {4} ₁₀ ,, с 60 вершинами, 1500 ребрами, 20000 граней, 150000 ячеек, 600000 4-граней, 1000000 5-граней

Обобщенные 6-кубы

Обобщенные 6-кубы имеют правильную конструкцию:и призматическая конструкция, как, произведение шести p -угольных 1-многогранников. Элементы представляют собой обобщенные кубы меньшей размерности.

• 
  Действительное {3,3,3,3,3,4} ,, с 64 вершинами, 192 ребрами, 240 гранями, 160 ячейками, 60 4-гранями и 12 5-гранями.
• 
  ₃ {4} ₂ {3} ₂ {3} ₂ {3} ₂ {3} ₂ ,, с 729 вершинами, 1458 ребрами, 1215 гранями, 540 ячейками, 135 4-гранями и 18 5-гранями.
• 
  ₄ {4} ₂ {3} ₂ {3} 2 _{{3} 2} {3} ₂ ,, с 4096 вершинами, 6144 ребрами, 3840 гранями, 1280 ячейками, 240 4-гранями и 24 5-гранями.
• 
  ₅ {4} ₂ {3} _{2 {3}} 2 {3} ₂ {3} ₂ ,, с 15625 вершинами, 18750 ребрами, 9375 гранями, 2500 ячейками, 375 4-гранями и 30 5-гранями.

Перечисление правильных сложных апейротопов

Коксетер перечислил этот список незвездных правильных сложных апейротопов или сот. ^[28]

Для каждого измерения существует 12 апейротопов, обозначенных как δ.^{п , р}
_н+1существует в любых измерениях , или если p = q =2. Коксетер называет эти обобщенные кубические соты для n >2. ^[29] ${\displaystyle \mathbb {C} ^{n}}$ ${\displaystyle \mathbb {R} ^{n}}$

Каждый из них имеет пропорциональное количество элементов, заданное как:

k-граней = , где и n ! обозначает факториал числа n . ${\displaystyle {n \choose k}p^{n-k}r^{k}}$ ${\displaystyle {n \choose m}={\frac {n!}{m!\,(n-m)!}}}$

Регулярные комплексные 1-многогранники

Единственный правильный комплексный 1-многогранник — это _∞ {}, или. Его реальным представлением является апейрогон , {∞} или.

Правильные сложные апейрогоны

Некоторые подгруппы апейрогональных групп Шепарда

11 сложных апейрогонов _p { q } _r , внутренние края которых окрашены в голубой цвет, а края вокруг одной вершины окрашены индивидуально. Вершины показаны в виде маленьких черных квадратов. Ребра рассматриваются как p -сторонние правильные многоугольники, а фигуры вершин являются r -угольными.

Квазиправильный апейрогонпредставляет собой смесь двух правильных апейрогонови, здесь видно с синими и розовыми краями.имеет только один цвет ребер, поскольку q нечетно, что делает его двойным покрытием.

Комплексные апейрогоны ранга 2 обладают симметрией _p [ q ] _r , где 1/ p + 2/ q + 1/ r = 1. Коксетер выражает их как δ^{п , р}
₂где q ограничено так, чтобы удовлетворять q = 2/(1 – ( p + r )/ pr ) . ^[30]

Есть 8 решений:

Имеются два исключенных решения нечетные q и неравные p и r : ₁₀ [5] ₂ и ₁₂ [3] ₄ , или и .

Правильный комплексный апейрогон _p { q } _r имеет p -ребра и r -угольные вершинные фигуры. Двойственный апейрогон к _p { q } _r — это _r { q } _p . Апейрогон вида _p { q } _p самодвойственный. Группы вида _p [2 q ] ₂ обладают полусимметрией _p [ q ] _p , поэтому правильный апейрогонто же самое, что и квазирегулярный. ^[31]

Апейрогоны могут быть представлены на плоскости Аргана с четырьмя различными расположениями вершин. Апейрогоны вида ₂ { q } _r имеют расположение вершин { q /2, p }. Форма _p { q } ₂ имеет расположение вершин как r { p , q /2}. Апейрогоны формы _p {4} _r имеют расположение вершин { p , r }.

Включая аффинные узлы и , существует еще 3 бесконечных решения: _∞ [2] _∞ , _∞ [4] ₂ , _∞ [3] ₃ и ${\displaystyle \mathbb {C} ^{2}}$,, и. Первая является подгруппой индекса 2 второй. Вершины этих апейрогонов существуют в . ${\displaystyle \mathbb {C} ^{1}}$

Правильные сложные апейроэдры

Имеется 22 правильных комплексных апейроэдра вида _p { a } _q { b } _r . 8 самодуальны ( p = r и a = b ), а 14 существуют как двойственные пары многогранников. Три из них вполне реальны ( p = q = r =2).

Коксетер символизирует 12 из них как δ.^{п , р}
₃или _p {4} ₂ {4} _r — правильная форма произведения апейротопа δ^{п , р}
₂× δ^{п , р}
₂или _p { q } _r × _p { q } _r , где q определяется из p и r .

такой же как, а также, для p , r =2,3,4,6. Также"=". ^[33]

Регулярные сложные 3-апейротопы

В . имеется 16 правильных сложных апейротопов . Коксетер выражает 12 из них через δ ${\displaystyle \mathbb {C} ^{3}}$^{п , р}
₃где q ограничено так, чтобы удовлетворять q = 2/(1 – ( p + r )/ pr ) . Их также можно разложить на апейротопы продуктов:"=". Первый случай — кубические соты . ${\displaystyle \mathbb {R} ^{3}}$

Регулярные сложные 4-апейротопы

В . имеется 15 правильных сложных апейротопов . Коксетер выражает 12 из них через δ ${\displaystyle \mathbb {C} ^{4}}$^{п , р}
₄где q ограничено так, чтобы удовлетворять q = 2/(1 – ( p + r )/ pr ) . Их также можно разложить на апейротопы продуктов:"=". Первый случай — тессерактические соты . Соты с 16 ячейками и соты с 24 ячейками являются реальными решениями. Последнее полученное решение содержит элементы многогранника Виттинга . ${\displaystyle \mathbb {R} ^{4}}$

Регулярные сложные 5-апейротопы и выше

Существует только 12 правильных комплексных апейротопов не ниже, чем ^[35] , выраженных δ ${\displaystyle \mathbb {C} ^{5}}$^{п , р}
_нгде q ограничено так, чтобы удовлетворять q = 2/(1 – ( p + r )/ pr ) . Их также можно разложить на произведение n апейрогонов:..."=".... Первый случай — это настоящие соты гиперкуба . ${\displaystyle \mathbb {R} ^{n}}$

полигон Ван Осса

Красный квадратный многоугольник Ван Осса в плоскости ребра и центра правильного октаэдра.

Многоугольник Ван Осса — это правильный многоугольник на плоскости (вещественной плоскости или унитарной плоскости ), в котором лежат как ребро, так и центроид правильного многогранника, и образованный из элементов многогранника. Не все правильные многогранники имеют многоугольники Ван Осса. ${\displaystyle \mathbb {R} ^{2}}$ ${\displaystyle \mathbb {C} ^{2}}$

Например, многоугольники Ван Осса настоящего октаэдра — это три квадрата, плоскости которых проходят через его центр. Напротив, куб не имеет многоугольника Ван Осса, потому что плоскость от края до центра пересекает по диагонали две квадратные грани, а два ребра куба, лежащие в плоскости, не образуют многоугольник.

Бесконечные соты также имеют апейрогоны Ван Осса . Например, вещественная квадратная мозаика и треугольная мозаика имеют апейрогоны {∞} ван Осса. ^[36]

Если он существует, то многоугольник Ван Осса правильного комплексного многогранника вида _p { q } _r { s } _t ... имеет p -рёбра.

Неправильные комплексные многогранники

Произведение сложных многогранников

Некоторые сложные многогранники можно представить в виде декартовых произведений . Эти многогранники-продукты не являются строго правильными, поскольку они будут иметь более одного типа граней, но некоторые из них могут представлять более низкую симметрию правильных форм, если все ортогональные многогранники идентичны. Например, произведение _p {}× _p {} илидвух одномерных многогранников совпадает с регулярным _p {4} ₂ или. Более общие продукты, такие как _p {}× _q {}, имеют вещественные представления в виде 4-мерных дуопризм p - q . Двойственный многограннику-продукту можно записать в виде суммы _p {}+ _q {} и иметь действительные представления в виде 4-мерной дуопирамиды p - q . Симметрия _p {}+ _p {} может быть удвоена как правильный комплексный многогранник ₂ {4} _p или .

Аналогично, комплексный многогранник можно построить как тройное произведение: _p {}× _p {}× _p {} или ${\displaystyle \mathbb {C} ^{3}}$то же самое, что и обычный обобщенный куб , _p {4} ₂ {3} ₂ или, а также произведение _p {4} ₂ × _p {} или. ^[37]

Квазиправильные многоугольники

Квазиправильный многоугольник – это усечение правильного многоугольника. Квазиправильный многоугольниксодержит альтернативные ребра правильных многоугольникови. Квазиправильный многоугольник имеет p вершин на p-ребрах правильной формы.

Квазиправильные апейрогоны

Существует семь квазиправильных комплексных апейрогонов, которые чередуют ребра правильного апейрогона и правильного двойственного ему апейрогона. Расположение вершин этих апейрогонов имеет вещественные представления с правильными и однородными мозаиками евклидовой плоскости. Последний столбец для апейрогона 6{3}6 не только самодвойственный, но и двойственный совпадает сам с собой с перекрывающимися шестиугольными ребрами, поэтому их квазиправильная форма также имеет перекрывающиеся шестиугольные ребра, поэтому его нельзя нарисовать двумя чередующимися цветами. как и другие. Симметрию самодуальных семейств можно удвоить, создав таким образом геометрию, идентичную правильной форме:"="

Квазиправильные многогранники

Пример усечения 3-обобщенного октаэдра, ₂ {3} ₂ {4} ₃ ,, до исправленного предела, показывая обведенные зелеными треугольниками грани в начале и синие ₂ {4} ₃ ,, фигуры вершин расширяются как новые грани.

Как и реальные многогранники, сложный квазиправильный многогранник можно построить как спрямление (полное усечение ) правильного многогранника. Вершины создаются посередине правильного многогранника, а грани правильного многогранника и его двойника располагаются поочередно по общим ребрам.

Например, p-обобщенный куб,, имеет p ³ вершин, 3 p ² ребер и 3 p p -обобщенных квадратных граней, а p -обобщенный октаэдр,, имеет 3 p вершин, 3 p ² ребер и p ³ треугольных граней. Средняя квазиправильная форма p -обобщенный кубооктаэдр,, имеет 3 p ² вершин, 3 p ³ ребер и 3 p + p ³ граней.

Также выпрямление гессенского многогранника. , является, квазиправильная форма, имеющая геометрию правильного комплексного многогранника..

Другие сложные многогранники с унитарными отражениями второго периода.

Другие нерегулярные комплексные многогранники могут быть построены внутри унитарных групп отражений, которые не образуют линейных графов Кокстера. На диаграммах Кокстера с петлями Коксетер отмечает интерьер особого периода, напримерили символ (1 ₁ 1 1) ³ и группа [1 1 1] ³ . ^{[38] [39]} Эти сложные многогранники систематически не исследовались, за исключением нескольких случаев.

Группаопределяется тремя унитарными отражениями, R ₁ , R ₂ , R ₃ , все порядка 2: R ₁ ² = R ₁ ² = R ₃ ² = (R ₁ R ₂ ) ³ = (R ₂ R ₃ ) ³ = (R ₃ R ₁ ) ³ = (R ₁ R ₂ R ₃ R ₁ ) ^p = 1. Период p можно рассматривать как двойное вращение в реальном времени . ${\displaystyle \mathbb {R} ^{4}}$

Как и во всех конструкциях Витхоффа , многогранниках, порожденных отражениями, количество вершин однокольцевого многогранника диаграммы Кокстера равно порядку группы, делённому на порядок подгруппы, из которой удален кольцевой узел. Например, реальный куб имеет диаграмму Кокстера., с октаэдрической симметрией порядок 48 и диэдральная симметрия подгруппыпорядка 6, поэтому количество вершин куба равно 48/6=8. Фасеты создаются путем удаления одного узла, самого дальнего от узла с кольцом, напримердля куба. Фигуры вершин генерируются путем удаления окольцованного узла и окольцовывания одного или нескольких связанных узлов, идля куба.

Коксетер представляет эти группы следующими символами. Некоторые группы имеют одинаковый порядок, но разную структуру, определяющую одно и то же расположение вершин в сложных многогранниках, но разные ребра и более высокие элементы, напримерис р ≠3. ^[40]

Коксетер называет некоторые из этих сложных многогранников почти правильными, поскольку они имеют правильные грани и фигуры вершин. Первый представляет собой форму более низкой симметрии обобщенного кросс-многогранника в . Второй — дробный обобщенный куб, сводящий p -ребра в отдельные вершины, оставляя обычные 2-ребра. Три из них связаны с конечным правильным косым многогранником в . ${\displaystyle \mathbb {C} ^{3}}$ ${\displaystyle \mathbb {R} ^{4}}$

Коксетер определяет другие группы с антиунитарными конструкциями, например эти три. Первый был обнаружен и нарисован Питером Макмалленом в 1966 году. ^[42]

Визуализации

• 
  (1 1 1 ₁ ⁴ ) ⁴ ,имеет 42 вершины, 168 ребер и 112 треугольных граней, видимых в этой 14-угольной проекции.
• 
  (1 ⁴ 1 ⁴ 1 ₁ ) ⁽³⁾ ,имеет 56 вершин, 168 ребер и 84 квадратных грани, как видно в этой 14-угольной проекции.
• 
  (1 1 2 ₂ ) ⁴ ,имеет 80 вершин, 640 ребер, 1280 треугольных граней и 640 тетраэдрических ячеек, видимых в этой 20-угольной проекции. ^[43]

Смотрите также

• Кватернионный многогранник

Примечания

1. Питер Орлик , Виктор Райнер, Энн В. Шеплер. Знаковое представление групп Шепарда . Математические Аннален . Март 2002 г., том 322, выпуск 3, стр. 477–492. DOI:10.1007/s002080200001 [1]
2. Коксетер, Правильные комплексные многогранники, с. 115
3. Коксетер, Правильные комплексные многогранники , 11.3 Многоугольник Петри , простой h -угольник, образованный орбитой флага (O ₀ , O ₀ O ₁ ) для произведения двух порождающих отражений любого незвездного правильного комплексного многоугольника, p ₁ { q } п ₂ .
4. Комплексные правильные многогранники, 11.1 Правильные комплексные многоугольники стр.103
5. Шепард, 1952; «Именно из подобных соображений мы выводим понятие внутренней части многогранника, и будет видно, что в унитарном пространстве, где числа не могут быть упорядочены таким образом, такое понятие внутренней части невозможно. [Парабрейк] Следовательно. ... мы должны рассматривать унитарные многогранники как конфигурации».
6. Коксетер, Правильные комплексные многогранники, с. 96
7. Коксетер, Правильные комплексные многогранники, с. xiv
8. Коксетер, Комплексные правильные многогранники, с. 177, таблица III
9. Лерер и Тейлор 2009, с. 87
10. Коксетер, Правильные комплексные многогранники, Таблица IV. Правильные многоугольники. стр. 178–179.
11. Комплексные многогранники, 8.9 Двумерный случай , с. 88
12. Правильные комплексные многогранники, Коксетер, стр. 177-179.
13. Коксетер, Правильные комплексные многогранники, с. 108
14. Коксетер, Правильные комплексные многогранники, с. 109
15. Коксетер, Правильные комплексные многогранники, с. 111
16. Коксетер, Правильные комплексные многогранники, с. 30 схема и стр. 47 индексов для 8 трехгранников
17. Коксетер, Правильные комплексные многогранники, с. 110
18. Коксетер, Правильные комплексные многогранники, с. 48
19. Коксетер, Правильные комплексные многогранники, с. 49
20. Коксетер, Правильные комплексные многогранники, стр. 116–140.
21. Коксетер, Правильные комплексные многогранники, стр. 118–119.
22. Комплексные правильные многогранники, стр.29
23. Коксетер, Правильные комплексные многогранники, Таблица V. Незвездные правильные многогранники и 4-многогранники. п. 180.
24. Коксетер, Калейдоскопы - Избранные сочинения HSM Коксетера , Статья 25 Удивительные отношения между унитарными группами отражения , стр. 431.
25. Коксетер, Правильные комплексные многогранники, с. 131
26. Коксетер, Правильные комплексные многогранники, с. 126
27. Коксетер, Правильные комплексные многогранники, с. 125
28. Коксетер, Правильные комплексные многогранники, Таблица VI. Обычные соты. п. 180.
29. Комплексный правильный многогранник, стр.174
30. Коксетер, Правильные комплексные многогранники, Таблица VI. Обычные соты. п. 111, 136.
31. Коксетер, Правильные комплексные многогранники, Таблица IV. Правильные многоугольники. стр. 178–179.
32. Коксетер, Правильные комплексные многогранники, 11.6 апейрогонов, стр. 111-112.
33. Коксетер, Комплексные правильные многогранники, стр.140
34. Коксетер, Правильные комплексные многогранники, стр. 139-140.
35. Комплексные правильные многогранники, стр.146
36. Комплексные правильные многогранники, стр.141
37. Коксетер, Правильные комплексные многогранники, стр. 118–119, 138.
38. Коксетер, Правильные комплексные многогранники, Глава 14, Почти правильные многогранники , стр. 156–174.
39. Коксетер, Группы, порожденные унитарными отражениями второго периода , 1956 г.
40. Коксетер , Конечные группы, порожденные унитарными отражениями , 1966, 4. Графические обозначения , Таблица n -мерных групп, порожденных n унитарными отражениями. стр. 422-423
41. Coxeter, Группы, порожденные унитарными отражениями второго периода (1956), Таблица III: Некоторые сложные многогранники, стр.413
42. Коксетер, Комплексные правильные многогранники, (1991), 14.6 Два многогранника Макмаллена с 84 квадратными гранями, стр.166-171
43. Коксетер, Комплексные правильные многогранники, стр. 172-173.

Рекомендации

• Коксетер, HSM и Мозер, WOJ; Генераторы и отношения для дискретных групп (1965), особенно стр. 67–80.
• Коксетер, HSM (1991), Правильные комплексные многогранники , издательство Кембриджского университета, ISBN 0-521-39490-2
• Коксетер, HSM и Шепард, GC; Портреты семейства сложных многогранников, Леонардо Том 25, № 3/4 (1992), стр. 239–244,
• Шепард, GC; Правильные комплексные многогранники , Учеб. Лондонская математика. Соц. Серия 3, Том 2 (1952), стр. 82–97.
• Г.К. Шепард , Дж.А. Тодд, Конечные унитарные группы отражений , Канадский математический журнал. 6(1954), 274-304, номер документа :10.4153/CJM-1954-028-3
• Густав И. Лерер и Дональд Э. Тейлор, Группы унитарного отражения , Cambridge University Press, 2009 г.

дальнейшее чтение

• Ф. Артур Шерк, Питер МакМаллен, Энтони К. Томпсон и Азия Ивич Вайс, редакторы: Калейдоскопы - Избранные сочинения HSM Coxeter. , Статья 25, Конечные группы, порожденные унитарными отражениями , стр. 415-425, Джон Уайли, 1995, ISBN 0-471-01003-0 
• МакМаллен, Питер ; Шульте, Эгон (декабрь 2002 г.), Абстрактные правильные многогранники (1-е изд.), Cambridge University Press , ISBN 0-521-81496-0Глава 9. Унитарные группы и эрмитовы формы , стр. 289–298.