Современная сеть Хопфилда

Нейронные сети

Современные сети Хопфилда ^{[1] [2]} (также известные как плотные ассоциативные памяти ^[3] ) являются обобщениями классических сетей Хопфилда , которые нарушают линейное соотношение масштабирования между числом входных признаков и числом сохраненных воспоминаний. Это достигается путем введения более сильных нелинейностей (либо в энергетической функции, либо в функциях активации нейронов), что приводит к сверхлинейной ^[3] (даже экспоненциальной ^[4] ) емкости памяти как функции числа нейронов признаков. Сеть по-прежнему требует достаточного количества скрытых нейронов. ^[5]

Основная теоретическая идея, лежащая в основе современных сетей Хопфилда, заключается в использовании энергетической функции и правила обновления, которые имеют более острый пик вокруг сохраненных воспоминаний в пространстве конфигураций нейронов по сравнению с классической сетью Хопфилда. ^[3]

Классические сети Хопфилда

Сети Хопфилда ^{[6] [7]} являются рекуррентными нейронными сетями с динамическими траекториями, сходящимися к состояниям аттрактора фиксированной точки и описываемыми энергетической функцией . Состояние каждого модельного нейрона определяется переменной, зависящей от времени , которая может быть выбрана как дискретная или непрерывная. Полная модель описывает математику того, как будущее состояние активности каждого нейрона зависит от известной настоящей или предыдущей активности всех нейронов. ${\textstyle i}$ ${\displaystyle V_{i}}$

В оригинальной модели ассоциативной памяти Хопфилда ^[6] переменные были бинарными, а динамика описывалась обновлением состояния нейронов по одному за раз. Была определена квадратичная по энергии функция, а динамика состояла в изменении активности каждого отдельного нейрона только в том случае, если это приводило к снижению общей энергии системы. Эта же идея была распространена на случай, когда непрерывная переменная представляет выход нейрона , и является монотонной функцией входного тока. Динамика стала выражаться в виде набора дифференциальных уравнений первого порядка , для которых «энергия» системы всегда уменьшалась. ^[7] Энергия в непрерывном случае имеет один член, который является квадратичным по (как в бинарной модели), и второй член, который зависит от функции усиления ( функции активации нейрона ). Обладая многими желательными свойствами ассоциативной памяти, обе эти классические системы страдают от малой емкости памяти, которая линейно масштабируется с числом входных признаков. ^[6] ${\displaystyle V_{i}}$ ${\displaystyle i}$ ${\displaystyle V_{i}}$ ${\displaystyle i}$ ${\displaystyle V_{i}}$ ${\displaystyle V_{i}}$

Дискретные переменные

Простой пример ^[3] современной сети Хопфилда можно записать в терминах бинарных переменных , которые представляют активное и неактивное состояние модельного нейрона . В этой формуле веса представляют матрицу векторов памяти (индекс перечисляет различные воспоминания, а индекс перечисляет содержимое каждого воспоминания, соответствующего -му нейрону-признаку), а функция является быстрорастущей нелинейной функцией. Правило обновления для отдельных нейронов (в асинхронном случае) можно записать в следующей форме, которая гласит, что для вычисления обновленного состояния -го нейрона сеть сравнивает две энергии: энергию сети с -м нейроном в состоянии ВКЛ и энергию сети с -м нейроном в состоянии ВЫКЛ, учитывая состояния оставшегося нейрона. Обновленное состояние -го нейрона выбирает состояние, которое имеет наименьшую из двух энергий. ^[3] ${\displaystyle V_{i}}$ ${\displaystyle V_{i}=+1}$ ${\displaystyle V_{i}=-1}$ ${\displaystyle i}$ $${\displaystyle E=-\sum \limits _{\mu =1}^{N_{\text{mem}}}F{\Big (}\sum \limits _{i=1}^{N_{f}}\xi _{\mu i}V_{i}{\Big )}}$$ ${\textstyle \xi _{\mu i}}$ ${\displaystyle \mu =1...N_{\text{mem}}}$ ${\displaystyle i=1...N_{f}}$ ${\displaystyle i}$ ${\displaystyle F(x)}$ $${\displaystyle V_{i}^{(t+1)}=\operatorname {sign} {\bigg [}\sum \limits _{\mu =1}^{N_{\text{mem}}}{\bigg (}F{\Big (}\xi _{\mu i}+\sum \limits _{j\neq i}\xi _{\mu j}V_{j}^{(t)}{\Big )}-F{\Big (}-\xi _{\mu i}+\sum \limits _{j\neq i}\xi _{\mu j}V_{j}^{(t)}{\Big )}{\bigg )}{\bigg ]}}$$ ${\textstyle i}$ ${\displaystyle i}$ ${\displaystyle i}$ ${\displaystyle i}$

В предельном случае, когда нелинейная энергетическая функция является квадратичной, эти уравнения сводятся к знакомой энергетической функции и правилу обновления для классической двоичной сети Хопфилда. ^[6] ${\displaystyle F(x)=x^{2}}$

Емкость памяти этих сетей может быть рассчитана для случайных бинарных паттернов. Для функции мощности энергии максимальное количество воспоминаний, которые могут быть сохранены и извлечены из этой сети без ошибок, определяется как ^[3] Для экспоненциальной функции энергии емкость памяти экспоненциальна по числу нейронов признаков ^[4] ${\displaystyle F(x)=x^{n}}$ $${\displaystyle N_{\text{mem}}^{\max }\approx {\frac {1}{2(2n-3)!!}}{\frac {N_{f}^{n-1}}{\ln(N_{f})}}}$$ ${\textstyle F(x)=e^{x}}$ $${\displaystyle N_{\text{mem}}^{\max }\approx 2^{N_{f}/2}}$$

Непрерывные переменные

Рис.1 Пример непрерывной современной сети Хопфилда с нейронами-признаками и нейронами памяти (скрытыми) с симметричными синаптическими связями между ними. ${\textstyle N_{f}=5}$ ${\displaystyle N_{\text{mem}}=11}$

Современные сети Хопфилда или плотные ассоциативные памяти лучше всего понимать в непрерывных переменных и непрерывном времени. ^{[1] [5]} Рассмотрим архитектуру сети, показанную на рис. 1, и уравнения для эволюции состояния нейронов ^[5]

где токи нейронов признаков обозначены как , а токи нейронов памяти обозначены как ( обозначает скрытые нейроны). Между нейронами признаков или нейронами памяти нет синаптических связей. Матрица обозначает силу синапсов от нейрона признака к нейрону памяти . Предполагается, что синапсы симметричны, так что одно и то же значение характеризует другой физический синапс от нейрона памяти к нейрону признака . Выходы нейронов памяти и нейронов признаков обозначены как и , которые являются нелинейными функциями соответствующих токов. В общем случае эти выходы могут зависеть от токов всех нейронов в этом слое, так что и . Удобно определить эти функции активации как производные функций Лагранжа для двух групп нейронов ${\textstyle x_{i}}$ ${\displaystyle h_{\mu }}$ ${\displaystyle h}$ ${\displaystyle \xi _{\mu i}}$ ${\displaystyle i}$ ${\displaystyle \mu }$ ${\displaystyle \mu }$ ${\displaystyle i}$ ${\displaystyle f_{\mu }}$ ${\displaystyle g_{i}}$ ${\displaystyle f_{\mu }=f(\{h_{\mu }\})}$ ${\textstyle g_{i}=g(\{x_{i}\})}$

Таким образом, конкретная форма уравнений для состояний нейронов полностью определяется после указания функций Лагранжа. Наконец, постоянные времени для двух групп нейронов обозначаются как и , — входной ток в сеть, который может управляться представленными данными. ${\displaystyle \tau _{f}}$ ${\displaystyle \tau _{h}}$ ${\displaystyle I_{i}}$

Рис.2 Эффективная теория на нейронах признаков для различных общих выборов функций Лагранжа. Модель A сводится к моделям, изученным в ^{[3] [4]} в зависимости от выбора функции активации, модель B сводится к модели, изученной в ^[1] , модель C сводится к модели. ^[5]

Общие системы нелинейных дифференциальных уравнений могут иметь много сложных поведений, которые могут зависеть от выбора нелинейностей и начальных условий. Однако для сетей Хопфилда это не так — динамические траектории всегда сходятся к состоянию аттрактора фиксированной точки. Это свойство достигается, поскольку эти уравнения специально спроектированы так, чтобы они имели базовую энергетическую функцию ^[5]

Члены, сгруппированные в квадратных скобках, представляют собой преобразование Лежандра функции Лагранжа относительно состояний нейронов. Если матрицы Гессе функций Лагранжа являются положительно полуопределенными, то функция энергии гарантированно убывает на динамической траектории ^[5]

Это свойство позволяет доказать, что система динамических уравнений, описывающая временную эволюцию активности нейронов, в конечном итоге достигнет состояния аттрактора фиксированной точки.

В определенных ситуациях можно предположить, что динамика скрытых нейронов уравновешивается в гораздо более быстром масштабе времени по сравнению с нейронами признаков, . В этом случае решение стационарного состояния второго уравнения в системе ( 1 ) может быть использовано для выражения токов скрытых единиц через выходы нейронов признаков. Это позволяет свести общую теорию ( 1 ) к эффективной теории только для нейронов признаков. Результирующие эффективные правила обновления и энергии для различных общих выборов функций Лагранжа показаны на рис. 2. В случае логарифмически-суммовой экспоненциальной функции Лагранжа правило обновления (если оно применено один раз) для состояний нейронов признаков является механизмом внимания ^[1], обычно используемым во многих современных системах ИИ (см. ссылку ^[5] для вывода этого результата из непрерывной временной формулировки). ${\textstyle \tau _{h}\ll \tau _{f}}$

Связь с классической сетью Хопфилда с непрерывными переменными

Классическая формулировка непрерывных сетей Хопфилда ^[6] может быть понята ^[5] как особый предельный случай современных сетей Хопфилда с одним скрытым слоем. Непрерывные сети Хопфилда для нейронов с градуированным откликом обычно описываются ^[6] динамическими уравнениями

и энергетическая функция

где , а — обратная функция активации . Эта модель является частным случаем класса моделей, называемых моделями A, ^[5] со следующим выбором функций Лагранжа ${\textstyle V_{i}=g(x_{i})}$ ${\displaystyle g^{-1}(z)}$ ${\displaystyle g(x)}$

что, согласно определению ( 2 ), приводит к функциям активации

Если мы интегрируем скрытые нейроны, то система уравнений ( 1 ) сводится к уравнениям для характерных нейронов ( 5 ) с , а общее выражение для энергии ( 3 ) сводится к эффективной энергии ${\displaystyle T_{ij}=\sum \limits _{\mu =1}^{N_{h}}\xi _{\mu i}\xi _{\mu j}}$

В то время как первые два члена в уравнении ( 6 ) такие же, как в уравнении ( 9 ), третьи члены выглядят поверхностно по-другому. В уравнении ( 9 ) это преобразование Лежандра лагранжиана для нейронов признаков, тогда как в ( 6 ) третий член является интегралом обратной функции активации. Тем не менее, эти два выражения фактически эквивалентны, поскольку производные функции и ее преобразования Лежандра являются обратными функциями друг друга. Самый простой способ увидеть, что эти два члена явно равны, — это продифференцировать каждый из них по . Результаты этих дифференцирований для обоих выражений равны . Таким образом, два выражения равны с точностью до аддитивной константы. Это завершает доказательство ^[5] того, что классическая сеть Хопфилда с непрерывными состояниями ^[6] является частным предельным случаем современной сети Хопфилда ( 1 ) с энергией ( 3 ). ${\displaystyle x_{i}}$ ${\displaystyle x_{i}g(x_{i})'}$

Общая формулировка

Рис.3 Диаграмма связности полносвязной современной сети Хопфилда, состоящей из пяти нейронов. Синаптические веса описываются симметричной матрицей . ${\displaystyle W_{IJ}}$

Биологические нейронные сети имеют большую степень гетерогенности с точки зрения различных типов клеток. В этом разделе описывается математическая модель полностью связанной сети Modern Hopfield, предполагающая крайнюю степень гетерогенности: каждый отдельный нейрон отличается. ^[8] В частности, энергетическая функция и соответствующие динамические уравнения описываются, предполагая, что каждый нейрон имеет свою собственную функцию активации и кинетическую шкалу времени. Предполагается, что сеть полностью связана, так что каждый нейрон связан с каждым другим нейроном с помощью симметричной матрицы весов , индексов и перечисления различных нейронов в сети, см. рис. 3. Самый простой способ математически сформулировать эту задачу — определить архитектуру с помощью функции Лагранжа , которая зависит от активности всех нейронов в сети. Функция активации для каждого нейрона определяется как частная производная лагранжиана относительно активности этого нейрона. ${\displaystyle W_{IJ}}$ ${\displaystyle I}$ ${\displaystyle J}$ ${\displaystyle L(\{x_{I}\})}$

С биологической точки зрения можно рассматривать как аксональный выход нейрона . В простейшем случае, когда лагранжиан аддитивен для разных нейронов, это определение приводит к активации, которая является нелинейной функцией активности этого нейрона. Для неаддитивных лагранжианов эта функция активации может зависеть от активности группы нейронов. Например, она может содержать контрастную (softmax) или дивизионную нормализацию. Динамические уравнения, описывающие временную эволюцию данного нейрона, задаются как ^[8] ${\displaystyle g_{I}}$ ${\displaystyle I}$

Это уравнение относится к классу моделей, называемых моделями частоты срабатывания в нейронауке. Каждый нейрон собирает аксональные выходы от всех нейронов, взвешивает их с помощью синаптических коэффициентов и производит свою собственную зависящую от времени активность . Временная эволюция имеет постоянную времени , которая в общем случае может быть разной для каждого нейрона. Эта сеть имеет глобальную энергетическую функцию ^[8] ${\displaystyle I}$ ${\displaystyle g_{J}}$ ${\displaystyle W_{IJ}}$ ${\displaystyle x_{I}}$ ${\displaystyle \tau _{I}}$

где первые два члена представляют собой преобразование Лежандра функции Лагранжа относительно токов нейронов . Временная производная этой энергетической функции может быть вычислена на динамических траекториях, ведущих к (см. ^[8] для получения подробной информации) ${\displaystyle x_{I}}$

Последний знак неравенства выполняется при условии, что матрица (или ее симметричная часть) является положительно полуопределенной. Если, в дополнение к этому, функция энергии ограничена снизу, нелинейные динамические уравнения гарантированно сходятся к состоянию аттрактора с фиксированной точкой. Преимущество формулировки этой сети в терминах функций Лагранжа состоит в том, что она позволяет легко экспериментировать с различными вариантами выбора функций активации и различными архитектурными расположениями нейронов. Для всех этих гибких вариантов условия сходимости определяются свойствами матрицы и существованием нижней границы для функции энергии. ${\displaystyle M_{IK}}$ ${\displaystyle M_{IJ}}$

Иерархическая ассоциативная сеть памяти

Рис.4 Диаграмма связей многослойной иерархической ассоциативной сети памяти. ^[8] Каждый слой может иметь разное количество нейронов, разную функцию активации и разную временную шкалу. Веса прямой связи и веса обратной связи равны.

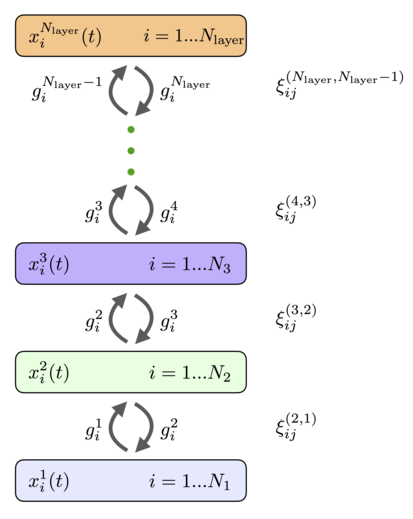
Нейроны могут быть организованы в слои так, что каждый нейрон в данном слое имеет одну и ту же функцию активации и одинаковую динамическую временную шкалу. Если предположить, что между нейронами внутри слоя нет горизонтальных связей (латеральных связей) и нет связей с пропусками слоев, общая полностью связанная сеть ( 11 ), ( 12 ) сводится к архитектуре, показанной на рис. 4. Она имеет слои рекуррентно связанных нейронов с состояниями, описываемыми непрерывными переменными и функциями активации , индекс перечисляет слои сети, а индекс перечисляет отдельные нейроны в этом слое. Функции активации могут зависеть от активности всех нейронов в слое. Каждый слой может иметь разное количество нейронов . Эти нейроны рекуррентно связаны с нейронами в предыдущем и последующем слоях. Матрицы весов, которые соединяют нейроны в слоях , обозначаются как (порядок верхних индексов для весов совпадает с порядком нижних индексов, в примере выше это означает, что индекс нумерует нейроны в слое , а индекс нумерует нейроны в слое ). Веса прямой связи и веса обратной связи равны. Динамические уравнения для состояний нейронов можно записать как ^[8] ${\displaystyle N_{\text{layer}}}$ ${\displaystyle x_{i}^{A}}$ ${\displaystyle g_{i}^{A}}$ ${\displaystyle A}$ ${\displaystyle i}$ ${\displaystyle N_{A}}$ ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle \xi _{ij}^{(A,B)}}$ ${\displaystyle i}$ ${\displaystyle A}$ ${\displaystyle j}$ ${\displaystyle B}$

с граничными условиями

Главное отличие этих уравнений от обычных сетей прямого распространения — наличие второго члена, который отвечает за обратную связь от более высоких слоев. Эти сигналы сверху вниз помогают нейронам в нижних слоях принять решение об их реакции на предъявленные стимулы. Следуя общему рецепту, удобно ввести функцию Лагранжа для -го скрытого слоя, которая зависит от активности всех нейронов в этом слое. ^[8] Функции активации в этом слое можно определить как частные производные функции Лагранжа ${\displaystyle L^{A}(\{x_{i}^{A}\})}$ ${\displaystyle A}$

При этих определениях функция энергии (Ляпунова) имеет вид ^[8]

Если функции Лагранжа или, что эквивалентно, функции активации выбраны таким образом, что гессианы для каждого слоя являются положительно полуопределенными, а общая энергия ограничена снизу, эта система гарантированно сходится к состоянию аттрактора с фиксированной точкой. Временная производная этой энергетической функции определяется как ^[8]

Таким образом, иерархическая слоистая сеть действительно является сетью аттракторов с глобальной энергетической функцией. Эта сеть описывается иерархическим набором синаптических весов, которые могут быть изучены для каждой конкретной проблемы.

Ссылки

1. Рамзауэр, Хуберт; и др. (2021). «Сети Хопфилда — это все, что вам нужно». Международная конференция по представлениям обучения . arXiv : 2008.02217 .
2. "Hopfield Networks is All You Need". hopfield-layers . 2020-08-25. Архивировано из оригинала 26 марта 2023 г. Получено 2023-05-04 .
3. Кротов, Дмитрий; Хопфилд, Джон (2016). «Плотная ассоциативная память для распознавания образов». Neural Information Processing Systems . 29 : 1172–1180. arXiv : 1606.01164 .
4. Demircigil, Mete; et al. (2017). «О модели ассоциативной памяти с огромной емкостью хранения». Журнал статистической физики . 168 (2): 288–299. arXiv : 1702.01929 . Bibcode : 2017JSP...168..288D. doi : 10.1007/s10955-017-1806-y. S2CID  119317128.
5. Кротов, Дмитрий; Хопфилд, Джон (2021). «Проблема большой ассоциативной памяти в нейробиологии и машинном обучении». Международная конференция по представлениям обучения . arXiv : 2008.06996 .
6. Хопфилд, Джон (1982). «Нейронные сети и физические системы с возникающими коллективными вычислительными способностями». Труды Национальной академии наук . 79 (8): 2554–2558. Bibcode : 1982PNAS...79.2554H. doi : 10.1073 /pnas.79.8.2554 . PMC 346238. PMID  6953413. 
7. Хопфилд, Джон (1984). «Нейроны с градуированным ответом имеют коллективные вычислительные свойства, подобные свойствам двухуровневых нейронов». Труды Национальной академии наук . 81 (10): 3088–3092. Bibcode : 1984PNAS...81.3088H. doi : 10.1073/pnas.81.10.3088 . PMC 345226. PMID  6587342 . 
8. Кротов, Дмитрий (2021). «Иерархическая ассоциативная память». arXiv : 2107.06446 [cs.NE].