Спирограф

Устройство для геометрического черчения

Спирограф — это геометрическое устройство для рисования, которое создает математические кривые рулетки , известные как гипотрохоиды и эпитрохоиды . Известная игрушечная версия была разработана британским инженером Денисом Фишером и впервые продана в 1965 году.

Название является зарегистрированной торговой маркой Hasbro Inc. с 1998 года после покупки компании, которая приобрела компанию Denys Fisher. Бренд Spirograph был перезапущен по всему миру в 2013 году с его оригинальными конфигурациями продукта компанией Kahootz Toys .

История

Рисование узоров с помощью кольца и колеса спирографа

Уличный торговец в Форт-Кочи, Индия, демонстрирует спирографы, которые он продает.

В 1827 году английский архитектор и инженер греческого происхождения Питер Хьюберт Десвинь разработал и рекламировал «Спирограф» — устройство для создания сложных спиральных рисунков. Человек по имени Дж. Джоплинг вскоре заявил, что ранее изобрел подобные методы. ^[1] Работая в Вене между 1845 и 1848 годами, Десвинь построил версию машины, которая помогла бы предотвратить подделку банкнот, ^[2] поскольку любая из почти бесконечных вариаций рулеточных узоров, которые она могла производить, была чрезвычайно сложна для обратного проектирования. Математик Бруно Абаканович изобрел новое устройство «Спирограф» между 1881 и 1900 годами. Оно использовалось для вычисления площади, ограниченной кривыми. ^[3]

Игрушки для рисования на основе шестерёнок появились как минимум в 1908 году, когда в каталоге Sears появилась реклама Marvelous Wondergraph . ^{[4] [5]} Статья с описанием того, как сделать машинку для рисования Wondergraph, появилась в издании Boys Mechanic в 1913 году. ^[6]

Окончательная игрушка Spirograph была разработана британским инженером Денисом Фишером между 1962 и 1964 годами путем создания чертежных машин с деталями Meccano . Фишер выставил свой спирограф на Нюрнбергской международной ярмарке игрушек 1965 года . Впоследствии он был произведен его компанией. Права на распространение в США были приобретены компанией Kenner , Inc., которая представила его на рынке Соединенных Штатов в 1966 году и продвигала его как творческую детскую игрушку. Позднее Kenner представила Spirotot, Magnetic Spirograph, Spiroman и различные наборы сменных принадлежностей. ^[7]

В 2013 году бренд Spirograph был перезапущен по всему миру с оригинальными шестеренками и колесами от Kahootz Toys. Современные продукты используют сменную замазку вместо штифтов, чтобы удерживать неподвижные части на месте. Spirograph был игрушкой года в 1967 году и финалистом Toy of the Year в двух категориях в 2014 году. Kahootz Toys была приобретена PlayMonster LLC в 2019 году. ^[8]

Операция

Оригинальный спирограф, выпущенный в США, состоял из двух пластиковых колец разного размера (или статоров ) с зубьями шестерен как внутри, так и снаружи их окружностей. После того, как любое из этих колец было закреплено на месте (либо штифтами, либо с помощью клея, либо вручную), любое из нескольких предоставленных зубчатых колес (или роторов) — каждое с отверстиями для шариковой ручки — можно было вращать вокруг кольца, чтобы рисовать геометрические фигуры. Позже, суперспирограф представил дополнительные формы, такие как кольца, треугольники и прямые стержни. Все края каждой детали имеют зубцы для зацепления с любой другой деталью; меньшие шестерни помещаются внутри больших колец, но они также могут вращаться вдоль внешнего края колец или даже вокруг друг друга. Шестерни можно комбинировать во многих различных расположениях. Наборы часто включали разноцветные ручки, которые могли улучшить дизайн, меняя цвета, как показано в примерах, показанных здесь.

Новички часто проскальзывают, особенно при использовании отверстий около края больших колес, что приводит к ломаным или неровным линиям. Опытные пользователи могут научиться перемещать несколько деталей относительно друг друга (например, треугольник вокруг кольца, с кругом, «поднимающимся» с кольца на треугольник).

• 
  Анимация спирографа
• 
  Несколько дизайнов спирографа, нарисованных с помощью набора спирографа и нескольких разноцветных ручек.
• 
  Крупный план колеса спирографа

Математическая основа

Геометрическое построение для математического объяснения спирографа.

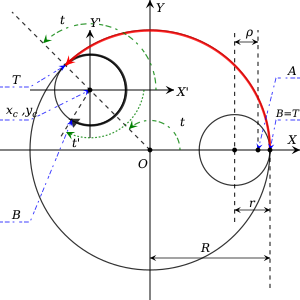
Рассмотрим фиксированную внешнюю окружность радиуса с центром в начале координат. Меньшая внутренняя окружность радиуса катится внутри и непрерывно касается ее. будет предполагаться, что никогда не проскальзывает (в реальном спирографе зубцы на обеих окружностях предотвращают такое проскальзывание). Теперь предположим, что точка, лежащая где-то внутри , расположена на расстоянии от центра . Эта точка соответствует отверстию для ручки во внутреннем диске реального спирографа. Без потери общности можно предположить, что в начальный момент точка находилась на оси. Чтобы найти траекторию, созданную спирографом, следуйте за точкой по мере того, как внутренняя окружность приходит в движение. ${\displaystyle C_{o}}$ ${\displaystyle R}$ ${\displaystyle C_{i}}$ ${\displaystyle r<R}$ ${\displaystyle C_{o}}$ ${\displaystyle C_{i}}$ ${\displaystyle C_{o}}$ ${\displaystyle A}$ ${\displaystyle C_{i}}$ ${\displaystyle \rho <r}$ ${\displaystyle C_{i}}$ ${\displaystyle A}$ ${\displaystyle A}$ ${\displaystyle X}$ ${\displaystyle A}$

Теперь отметьте две точки на и на . Точка всегда указывает место, где касаются две окружности. Точка , однако, будет перемещаться по , и ее начальное положение совпадает с . После приведения в движение против часовой стрелки вокруг , имеет вращение по часовой стрелке относительно своего центра. Расстояние, которое проходит точка, такое же, как и расстояние, пройденное точкой касания на , из-за отсутствия скольжения. ${\displaystyle T}$ ${\displaystyle C_{o}}$ ${\displaystyle B}$ ${\displaystyle C_{i}}$ ${\displaystyle T}$ ${\displaystyle B}$ ${\displaystyle C_{i}}$ ${\displaystyle T}$ ${\displaystyle C_{i}}$ ${\displaystyle C_{o}}$ ${\displaystyle C_{i}}$ ${\displaystyle B}$ ${\displaystyle C_{i}}$ ${\displaystyle T}$ ${\displaystyle C_{o}}$

Теперь определим новую (относительную) систему координат с началом в центре и осями, параллельными и . Пусть параметр будет углом, на который точка касания поворачивается на , а будет углом, на который поворачивается (т.е. на который перемещается) в относительной системе координат. Поскольку нет скольжения, расстояния, пройденные и вдоль их соответствующих окружностей, должны быть одинаковыми, поэтому ${\displaystyle (X',Y')}$ ${\displaystyle C_{i}}$ ${\displaystyle X}$ ${\displaystyle Y}$ ${\displaystyle t}$ ${\displaystyle T}$ ${\displaystyle C_{o}}$ ${\displaystyle t'}$ ${\displaystyle C_{i}}$ ${\displaystyle B}$ ${\displaystyle B}$ ${\displaystyle T}$

${\displaystyle tR=(t-t')r,}$

или эквивалентно,

${\displaystyle t'=-{\frac {R-r}{r}}t.}$

Обычно предполагается, что движение против часовой стрелки соответствует положительному изменению угла, а движение по часовой стрелке — отрицательному изменению угла. Знак минус в приведенной выше формуле ( ) учитывает это соглашение. ${\displaystyle t'<0}$

Пусть — координаты центра в абсолютной системе координат. Тогда представляет радиус траектории центра , который (опять же в абсолютной системе) совершает круговое движение таким образом: ${\displaystyle (x_{c},y_{c})}$ ${\displaystyle C_{i}}$ ${\displaystyle R-r}$ ${\displaystyle C_{i}}$

${\displaystyle {\begin{aligned}x_{c}&=(R-r)\cos t,\\y_{c}&=(R-r)\sin t.\end{aligned}}}$

Как определено выше, это угол поворота в новой относительной системе. Поскольку точка подчиняется обычному закону кругового движения, ее координаты в новой относительной системе координат равны ${\displaystyle t'}$ ${\displaystyle A}$ ${\displaystyle (x',y')}$

${\displaystyle {\begin{aligned}x'&=\rho \cos t',\\y'&=\rho \sin t'.\end{aligned}}}$

Чтобы получить траекторию в абсолютной (старой) системе координат, складываем эти два движения: ${\displaystyle A}$

${\displaystyle {\begin{aligned}x&=x_{c}+x'=(R-r)\cos t+\rho \cos t',\\y&=y_{c}+y'=(R-r)\sin t+\rho \sin t',\\\end{aligned}}}$

где определено выше. ${\displaystyle \rho }$

Теперь воспользуемся соотношением между и , полученным выше, чтобы получить уравнения, описывающие траекторию точки в терминах одного параметра : ${\displaystyle t}$ ${\displaystyle t'}$ ${\displaystyle A}$ ${\displaystyle t}$

${\displaystyle {\begin{aligned}x&=x_{c}+x'=(R-r)\cos t+\rho \cos {\frac {R-r}{r}}t,\\y&=y_{c}+y'=(R-r)\sin t-\rho \sin {\frac {R-r}{r}}t\\\end{aligned}}}$

(используя тот факт, что функция нечетная ) . ${\displaystyle \sin }$

Уравнение выше удобно представить в терминах радиуса и безразмерных параметров, описывающих структуру спирографа. А именно, пусть ${\displaystyle R}$ ${\displaystyle C_{o}}$

${\displaystyle l={\frac {\rho }{r}}}$

и

${\displaystyle k={\frac {r}{R}}.}$

Параметр показывает, насколько далеко точка расположена от центра . В то же время, показывает, насколько велик внутренний круг по отношению к внешнему . ${\displaystyle 0\leq l\leq 1}$ ${\displaystyle A}$ ${\displaystyle C_{i}}$ ${\displaystyle 0\leq k\leq 1}$ ${\displaystyle C_{i}}$ ${\displaystyle C_{o}}$

В настоящее время наблюдается, что

${\displaystyle {\frac {\rho }{R}}=lk,}$

и поэтому уравнения траектории принимают вид

${\displaystyle {\begin{aligned}x(t)&=R\left[(1-k)\cos t+lk\cos {\frac {1-k}{k}}t\right],\\y(t)&=R\left[(1-k)\sin t-lk\sin {\frac {1-k}{k}}t\right].\\\end{aligned}}}$

Параметр является параметром масштабирования и не влияет на структуру спирографа. Различные значения дадут похожие рисунки спирографа. ${\displaystyle R}$ ${\displaystyle R}$

Два крайних случая и приводят к вырожденным траекториям спирографа. В первом крайнем случае, когда , мы имеем простую окружность радиуса , соответствующую случаю, когда сжался в точку. (Деление на в формуле не является проблемой, поскольку обе функции и являются ограниченными.) ${\displaystyle k=0}$ ${\displaystyle k=1}$ ${\displaystyle k=0}$ ${\displaystyle R}$ ${\displaystyle C_{i}}$ ${\displaystyle k=0}$ ${\displaystyle \sin }$ ${\displaystyle \cos }$

Другой крайний случай соответствует радиусу внутреннего круга, совпадающему с радиусом внешнего круга , то есть . В этом случае траектория представляет собой одну точку. Интуитивно понятно, что слишком большой, чтобы катиться внутри того же размера без проскальзывания. ${\displaystyle k=1}$ ${\displaystyle C_{i}}$ ${\displaystyle r}$ ${\displaystyle R}$ ${\displaystyle C_{o}}$ ${\displaystyle r=R}$ ${\displaystyle C_{i}}$ ${\displaystyle C_{o}}$

Если , то точка находится на окружности . В этом случае траектории называются гипоциклоидами , а приведенные выше уравнения сводятся к уравнениям для гипоциклоиды. ${\displaystyle l=1}$ ${\displaystyle A}$ ${\displaystyle C_{i}}$

Смотрите также

• кардиоидный
• Апсидальная прецессия
• Циклограф
• Геометрический токарный станок
• Гильоширование
• Гармонограф
• Гипотрохоидный
• кривая Лиссажу
• Список периодических функций
• Пантограф
• Шестерня
• Роуз (математика)
• Розетта (орбита)
• Туманность Спирограф — планетарная туманность , которая демонстрирует изящную, похожую на спирограф филигрань.
• Туси пара

Ссылки

1. Найт, Джон И. (1828). «Журнал механики». Найт; Лейси – через Google Books.
2. «Спирограф и примеры узоров, нарисованных с его помощью | Коллекция Музея науки».
3. Гольдштейн, Кэтрин; Грей, Джереми; Риттер, Джим (1996). Математическая Европа: истории, мифы, идентичности. Издания МШ. п. 293. ИСБН 9782735106851. Получено 17 июля 2011 г.
4. Кавени, Венди. "CONTENTdm Collection: Compound Object Viewer". digitallibrary.imcpl.org . Получено 17 июля 2011 г.
5. Линдерман, Джим. "ArtSlant - Спирограф? Нет, ВОЛШЕБНЫЙ УЗОР!". artslant.com . Получено 17 июля 2011 г.
6. "From The Boy Mechanic (1913) - A Wondergraph". marcdatabase.com . 2004. Архивировано из оригинала 30 сентября 2011 г. Получено 17 июля 2011 г.
7. Купи, Тодд (17 августа 2015 г.). «Спирограф». ToyTales.ca .
8. "PlayMonster приобретает Kahootz Toys". 14 ноября 2019 г. Получено 26 февраля 2023 г.

Внешние ссылки

• Официальный сайт
• Воевудко, А.Е. (12 марта 2018 г.). «Географические кривые». Проект кода .