Статистика Максвелла-Больцмана

Статистическое распределение, используемое в механике многих частиц

Статистику Максвелла–Больцмана можно использовать для вывода распределения Максвелла–Больцмана скоростей частиц в идеальном газе . Показано: распределение скоростей для 10 ⁶ молекул кислорода при -100, 20 и 600 °C.

В статистической механике статистика Максвелла–Больцмана описывает распределение классических материальных частиц по различным энергетическим состояниям в тепловом равновесии . Она применима, когда температура достаточно высока или плотность частиц достаточно низка, чтобы сделать квантовые эффекты пренебрежимо малыми.

Ожидаемое число частиц с энергией для статистики Максвелла-Больцмана равно ${\displaystyle \varepsilon _{i}}$

${\displaystyle \langle N_{i}\rangle ={\frac {g_{i}}{e^{(\varepsilon _{i}-\mu )/kT}}}={\frac {N}{Z}}\,g_{i}e^{-\varepsilon _{i}/kT},}$

где:

• ${\displaystyle \varepsilon _{i}}$- энергия i - го энергетического уровня,
• ${\displaystyle \langle N_{i}\rangle }$- среднее число частиц в наборе состояний с энергией , ${\displaystyle \varepsilon _{i}}$
• ${\displaystyle g_{i}}$- вырождение уровня энергии i , то есть число состояний с энергией , которые тем не менее можно отличить друг от друга какими-то другими способами, ^{[nb 1]} ${\displaystyle \varepsilon _{i}}$
• μ — химический потенциал ,
• k — постоянная Больцмана ,
• T — абсолютная температура ,
• N — общее число частиц: $${\displaystyle N=\sum _{i}N_{i},}$$
• Z — это функция распределения : $${\displaystyle Z=\sum _{i}g_{i}e^{-\varepsilon _{i}/kT},}$$
• e — число Эйлера

Эквивалентно, число частиц иногда выражается как

${\displaystyle \langle N_{i}\rangle ={\frac {1}{e^{(\varepsilon _{i}-\mu )/kT}}}={\frac {N}{Z}}\,e^{-\varepsilon _{i}/kT},}$

где индекс i теперь указывает конкретное состояние, а не набор всех состояний с энергией , и . ${\displaystyle \varepsilon _{i}}$ ${\textstyle Z=\sum _{i}e^{-\varepsilon _{i}/kT}}$

История

Статистика Максвелла–Больцмана выросла из распределения Максвелла–Больцмана, скорее всего, как выжимка из базовой техники. ^{[ сомнительно – обсудить ]} Распределение было впервые выведено Максвеллом в 1860 году на эвристических основаниях. Позднее, в 1870-х годах, Больцман провел значительные исследования физических истоков этого распределения. Распределение может быть выведено на том основании, что оно максимизирует энтропию системы.

Применимость

Равновесные тепловые распределения для частиц с целым спином (бозоны), полуцелым спином (фермионы) и классических (бесспиновых) частиц. Средняя занятость показана в зависимости от энергии относительно химического потенциала системы , где — температура системы, а — постоянная Больцмана. ${\displaystyle \langle n\rangle }$ ${\displaystyle \epsilon }$ ${\displaystyle \mu }$ ${\displaystyle T}$ ${\displaystyle k_{B}}$

Статистика Максвелла–Больцмана используется для вывода распределения Максвелла–Больцмана идеального газа. Однако ее также можно использовать для расширения этого распределения на частицы с другим соотношением энергии и импульса , такие как релятивистские частицы (что приводит к распределению Максвелла–Юттнера ), и на другие, не трехмерные пространства.

Статистику Максвелла–Больцмана часто описывают как статистику «различимых» классических частиц. Другими словами, конфигурация частицы A в состоянии 1 и частицы B в состоянии 2 отличается от случая, когда частица B находится в состоянии 1, а частица A — в состоянии 2. Это предположение приводит к правильной (больцмановской) статистике частиц в энергетических состояниях, но дает нефизические результаты для энтропии, как это воплощено в парадоксе Гиббса .

В то же время, нет реальных частиц, которые обладают характеристиками, требуемыми статистикой Максвелла–Больцмана. Действительно, парадокс Гиббса разрешается, если мы рассматриваем все частицы определенного типа (например, электроны, протоны, фотоны и т. д.) как принципиально неразличимые. Как только это предположение сделано, статистика частиц меняется. Изменение энтропии в примере энтропии смешивания можно рассматривать как пример неэкстенсивной энтропии, возникающей из-за различимости двух типов смешиваемых частиц.

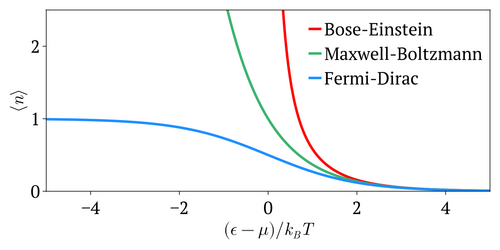
Квантовые частицы — это либо бозоны (следующие вместо этого статистике Бозе-Эйнштейна ), либо фермионы (подчиняющиеся принципу исключения Паули , следуя вместо этого статистике Ферми-Дирака ). Обе эти квантовые статистики приближаются к статистике Максвелла-Больцмана в пределе высокой температуры и низкой плотности частиц.

Производные

Статистику Максвелла–Больцмана можно вывести в различных статистических механических термодинамических ансамблях: ^[1]

• Большой канонический ансамбль , именно так.
• Канонический ансамбль , именно так.
• Микроканонический ансамбль , но только в термодинамическом пределе.

В каждом случае необходимо предполагать, что частицы не взаимодействуют друг с другом и что несколько частиц могут занимать одно и то же состояние и делать это независимо.

Вывод из микроканонического ансамбля

Предположим, у нас есть контейнер с огромным количеством очень маленьких частиц, все с идентичными физическими характеристиками (такими как масса, заряд и т. д.). Давайте назовем это системой . Предположим, что хотя частицы имеют идентичные свойства, они различимы. Например, мы могли бы идентифицировать каждую частицу, непрерывно наблюдая за их траекториями или размещая маркировку на каждой из них, например, рисуя разные числа на каждой из них, как это делается с лотерейными шарами.

Частицы движутся внутри этого контейнера во всех направлениях с большой скоростью. Поскольку частицы движутся с большой скоростью, они обладают некоторой энергией. Распределение Максвелла–Больцмана — это математическая функция, которая описывает, сколько частиц в контейнере имеют определенную энергию. Точнее, распределение Максвелла–Больцмана дает ненормализованную вероятность (это означает, что вероятности не составляют в сумме 1) того, что состояние, соответствующее определенной энергии, занято.

В общем случае может быть много частиц с одинаковым количеством энергии . Пусть число частиц с одинаковой энергией будет , число частиц, обладающих другой энергией, будет , и так далее для всех возможных энергий Чтобы описать эту ситуацию, мы говорим, что есть число заполнения энергетического уровня Если мы знаем все числа заполнения , то мы знаем полную энергию системы. Однако, поскольку мы можем различать, какие частицы занимают каждый энергетический уровень, набор чисел заполнения не полностью описывает состояние системы. Чтобы полностью описать состояние системы или микросостояние , мы должны точно указать, какие частицы находятся на каждом энергетическом уровне. Таким образом, когда мы подсчитываем число возможных состояний системы, мы должны подсчитывать каждое микросостояние, а не только возможные наборы чисел заполнения. ${\displaystyle \varepsilon }$ ${\displaystyle \varepsilon _{1}}$ ${\displaystyle N_{1}}$ ${\displaystyle \varepsilon _{2}}$ ${\displaystyle N_{2}}$ ${\displaystyle \{\varepsilon _{i}\mid i=1,2,3,\ldots \}.}$ ${\displaystyle N_{i}}$ ${\displaystyle i.}$ ${\displaystyle \{N_{i}\mid i=1,2,3,\ldots \},}$ ${\displaystyle \{N_{i}\mid i=1,2,3,\ldots \}}$

Для начала предположим, что на каждом энергетическом уровне существует только одно состояние (вырождения нет). Далее следует немного комбинаторного мышления, которое мало связано с точным описанием резервуара частиц. Например, предположим, что есть всего ящиков, помеченных . С помощью концепции комбинации мы могли бы вычислить, сколько существует способов упорядочить их в набор ящиков, где порядок шариков в каждом ящике не отслеживается. Сначала мы выбираем шарики из общего числа шариков, чтобы поместить их в ящик , и продолжаем выбирать для каждого ящика оставшиеся шарики, гарантируя, что каждый шарик помещен в один из ящиков. Общее количество способов, которыми шарики могут быть упорядочены, равно ${\displaystyle i}$ ${\displaystyle k}$ ${\displaystyle a,b,\ldots ,k}$ ${\displaystyle N}$ ${\displaystyle N_{a}}$ ${\displaystyle N}$ ${\displaystyle a}$

${\displaystyle {\begin{aligned}W&={\frac {N!}{N_{a}!{\cancel {(N-N_{a})!}}}}\times {\frac {\cancel {(N-N_{a})!}}{N_{b}!{\cancel {(N-N_{a}-N_{b})!}}}}\times {\frac {\cancel {(N-N_{a}-N_{b})!}}{N_{c}!{\cancel {(N-N_{a}-N_{b}-N_{c})!}}}}\times \cdots \times {\frac {\cancel {(N-\cdots -N_{\ell })!}}{N_{k}!(N-\cdots -N_{\ell }-N_{k})!}}\\[8pt]&={\frac {N!}{N_{a}!N_{b}!N_{c}!\cdots N_{k}!(N-N_{a}-\cdots -N_{\ell }-N_{k})!}}\end{aligned}}}$

Поскольку каждый шар был помещен в коробку , и мы упрощаем выражение как ${\displaystyle (N-N_{a}-N_{b}-\cdots -N_{k})!=0!=1}$

${\displaystyle W=N!\prod _{\ell =a,b,\ldots }^{k}{\frac {1}{N_{\ell }!}}}$

Это всего лишь мультиномиальный коэффициент , количество способов размещения N предметов в k ящиках, причем l -й ящик содержит N _l предметов, игнорируя перестановку предметов в каждом ящике.

Теперь рассмотрим случай, когда существует более одного способа поместить частицы в ящик (т.е. принимая во внимание проблему вырождения). Если -й ящик имеет "вырождение" , то есть у него есть "подящики" ( ящики с одинаковой энергией . Эти состояния/ящики с одинаковой энергией называются вырожденными состояниями.), так что любой способ заполнения -го ящика, при котором число в подящиках изменяется, является отдельным способом заполнения ящика, тогда количество способов заполнения i -го ящика должно быть увеличено на количество способов распределения объектов в "подящиках". Количество способов размещения различимых объектов в "подящиках" равно (первый объект может попасть в любой из ящиков, второй объект также может попасть в любой из ящиков и т.д.). Таким образом, количество способов , которыми общее количество частиц может быть классифицировано по энергетическим уровням в соответствии с их энергиями, в то время как каждый уровень имеет различные состояния, такие, что i -й уровень вмещает частицы, равно: ${\displaystyle N_{i}}$ ${\displaystyle i}$ ${\displaystyle i}$ ${\displaystyle g_{i}}$ ${\displaystyle g_{i}}$ ${\displaystyle g_{i}}$ ${\displaystyle \varepsilon _{i}}$ ${\displaystyle i}$ ${\displaystyle N_{i}}$ ${\displaystyle g_{i}}$ ${\displaystyle N_{i}}$ ${\displaystyle g_{i}}$ ${\displaystyle g_{i}^{N_{i}}}$ ${\displaystyle g_{i}}$ ${\displaystyle g_{i}}$ ${\displaystyle W}$ ${\displaystyle N}$ ${\displaystyle i}$ ${\displaystyle g_{i}}$ ${\displaystyle N_{i}}$

${\displaystyle W=N!\prod _{i}{\frac {g_{i}^{N_{i}}}{N_{i}!}}}$

Это форма для W, впервые полученная Больцманом . Фундаментальное уравнение Больцмана связывает термодинамическую энтропию S с числом микросостояний W , где k — постоянная Больцмана . Однако Гиббс указал , что приведенное выше выражение для W не дает экстенсивной энтропии и, следовательно, является ошибочным. Эта проблема известна как парадокс Гиббса . Проблема в том, что частицы, рассматриваемые приведенным выше уравнением, не являются неразличимыми . Другими словами, для двух частиц ( A и B ) на двух энергетических подуровнях популяция, представленная [A,B], считается отличной от популяции [B,A], в то время как для неразличимых частиц они таковыми не являются. Если мы проведем рассуждение для неразличимых частиц, мы придем к выражению Бозе–Эйнштейна для W : ${\displaystyle S=k\,\ln W}$

${\displaystyle W=\prod _{i}{\frac {(N_{i}+g_{i}-1)!}{N_{i}!(g_{i}-1)!}}}$

Распределение Максвелла–Больцмана следует из этого распределения Бозе–Эйнштейна для температур значительно выше абсолютного нуля, подразумевая, что . Распределение Максвелла–Больцмана также требует низкой плотности, подразумевая, что . При этих условиях мы можем использовать приближение Стирлинга для факториала: ${\displaystyle g_{i}\gg 1}$ ${\displaystyle g_{i}\gg N_{i}}$

${\displaystyle N!\approx N^{N}e^{-N},}$

написать:

${\displaystyle W\approx \prod _{i}{\frac {(N_{i}+g_{i})^{N_{i}+g_{i}}}{N_{i}^{N_{i}}g_{i}^{g_{i}}}}\approx \prod _{i}{\frac {g_{i}^{N_{i}}(1+N_{i}/g_{i})^{g_{i}}}{N_{i}^{N_{i}}}}}$

Используя тот факт, что для мы можем снова использовать приближение Стирлинга, чтобы записать: ${\displaystyle (1+N_{i}/g_{i})^{g_{i}}\approx e^{N_{i}}}$ ${\displaystyle g_{i}\gg N_{i}}$

${\displaystyle W\approx \prod _{i}{\frac {g_{i}^{N_{i}}}{N_{i}!}}}$

По сути, это деление на N ! исходного выражения Больцмана для W , и эта поправка называетсяправильный подсчет Больцмана .

Мы хотим найти , для которого функция максимизируется, принимая во внимание ограничение, что в контейнере есть фиксированное число частиц и фиксированная энергия . Максимумы и достигаются теми же значениями и , поскольку это проще сделать математически, мы вместо этого максимизируем последнюю функцию. Мы ограничиваем наше решение с помощью множителей Лагранжа, образующих функцию: ${\displaystyle N_{i}}$ ${\displaystyle W}$ ${\textstyle \left(N=\sum N_{i}\right)}$ ${\textstyle \left(E=\sum N_{i}\varepsilon _{i}\right)}$ ${\displaystyle W}$ ${\displaystyle \ln(W)}$ ${\displaystyle N_{i}}$

${\displaystyle f(N_{1},N_{2},\ldots ,N_{n})=\textstyle \ln(W)+\alpha (N-\sum N_{i})+\beta (E-\sum N_{i}\varepsilon _{i})}$

${\displaystyle \ln W=\ln \left[\prod _{i=1}^{n}{\frac {g_{i}^{N_{i}}}{N_{i}!}}\right]\approx \sum _{i=1}^{n}\left(N_{i}\ln g_{i}-N_{i}\ln N_{i}+N_{i}\right)}$

Окончательно

${\displaystyle f(N_{1},N_{2},\ldots ,N_{n})=\alpha N+\beta E+\sum _{i=1}^{n}\left(N_{i}\ln g_{i}-N_{i}\ln N_{i}+N_{i}-(\alpha +\beta \varepsilon _{i})N_{i}\right)}$

Для того чтобы максимизировать приведенное выше выражение, применим теорему Ферма (стационарные точки) , согласно которой локальные экстремумы, если они существуют, должны находиться в критических точках (частные производные обращаются в нуль):

${\displaystyle {\frac {\partial f}{\partial N_{i}}}=\ln g_{i}-\ln N_{i}-(\alpha +\beta \varepsilon _{i})=0}$

Решая приведенные выше уравнения ( ), приходим к выражению для : ${\displaystyle i=1\ldots n}$ ${\displaystyle N_{i}}$

${\displaystyle N_{i}={\frac {g_{i}}{e^{\alpha +\beta \varepsilon _{i}}}}}$

Подставляя это выражение в уравнение для и предполагая, что получаем: ${\displaystyle N_{i}}$ ${\displaystyle \ln W}$ ${\displaystyle N\gg 1}$

${\displaystyle \ln W=(\alpha +1)N+\beta E\,}$

или, переставляя:

${\displaystyle E={\frac {\ln W}{\beta }}-{\frac {N}{\beta }}-{\frac {\alpha N}{\beta }}}$

Больцман понял, что это всего лишь выражение интегрированного по Эйлеру фундаментального уравнения термодинамики . Определив E как внутреннюю энергию, интегрированное по Эйлеру фундаментальное уравнение утверждает, что:

${\displaystyle E=TS-PV+\mu N}$

где T — температура , P — давление, V — объем , а μ — химический потенциал . Уравнение Больцмана — это реализация того, что энтропия пропорциональна с константой пропорциональности, являющейся постоянной Больцмана . Используя уравнение состояния идеального газа ( PV  =  NkT ), немедленно следует, что и поэтому популяции теперь можно записать: ${\displaystyle S=k\ln W}$ ${\displaystyle \ln W}$ ${\displaystyle \beta =1/kT}$ ${\displaystyle \alpha =-\mu /kT}$

${\displaystyle N_{i}={\frac {g_{i}}{e^{(\varepsilon _{i}-\mu )/(kT)}}}}$

Обратите внимание, что приведенную выше формулу иногда записывают так:

${\displaystyle N_{i}={\frac {g_{i}}{e^{\varepsilon _{i}/kT}/z}}}$

где - абсолютная активность . ${\displaystyle z=\exp(\mu /kT)}$

В качестве альтернативы мы можем использовать тот факт, что

${\displaystyle \sum _{i}N_{i}=N}$

чтобы получить численность населения как

${\displaystyle N_{i}=N{\frac {g_{i}e^{-\varepsilon _{i}/kT}}{Z}}}$

где Z — это функция распределения, определяемая как:

${\displaystyle Z=\sum _{i}g_{i}e^{-\varepsilon _{i}/kT}}$

В приближении, где ε _i считается непрерывной переменной, приближение Томаса–Ферми дает непрерывное вырождение g, пропорциональное так, что: ${\displaystyle {\sqrt {\varepsilon }}}$

${\displaystyle {\frac {{\sqrt {\varepsilon }}\,e^{-\varepsilon /kT}}{\int _{0}^{\infty }{\sqrt {\varepsilon }}\,e^{-\varepsilon /kT}}}={\frac {{\sqrt {\varepsilon }}\,e^{-\varepsilon /kT}}{{\frac {\sqrt {\pi }}{2}}(kT)^{3/2}}}={\frac {2{\sqrt {\varepsilon }}\,e^{-\varepsilon /kT}}{\sqrt {\pi (kT)^{3}}}}}$

что является просто распределением Максвелла–Больцмана для энергии.

Вывод из канонического ансамбля

В приведенном выше обсуждении функция распределения Больцмана была получена путем прямого анализа множественностей системы. В качестве альтернативы можно использовать канонический ансамбль . В каноническом ансамбле система находится в тепловом контакте с резервуаром. В то время как энергия может свободно течь между системой и резервуаром, считается, что резервуар имеет бесконечно большую теплоемкость, чтобы поддерживать постоянную температуру T для объединенной системы.

В настоящем контексте предполагается, что наша система имеет уровни энергии с вырождениями . Как и прежде, мы хотели бы вычислить вероятность того, что наша система имеет энергию . ${\displaystyle \varepsilon _{i}}$ ${\displaystyle g_{i}}$ ${\displaystyle \varepsilon _{i}}$

Если наша система находится в состоянии , то для резервуара будет доступно соответствующее число микросостояний. Назовем это число . По предположению, объединенная система (из интересующей нас системы и резервуара) изолирована, поэтому все микросостояния равновероятны. Поэтому, например, если , мы можем заключить, что наша система в два раза чаще находится в состоянии , чем . В общем случае, если — вероятность того, что наша система находится в состоянии , ${\displaystyle \;s_{1}}$ ${\displaystyle \;\Omega _{R}(s_{1})}$ ${\displaystyle \;\Omega _{R}(s_{1})=2\;\Omega _{R}(s_{2})}$ ${\displaystyle \;s_{1}}$ ${\displaystyle \;s_{2}}$ ${\displaystyle \;P(s_{i})}$ ${\displaystyle \;s_{i}}$

${\displaystyle {\frac {P(s_{1})}{P(s_{2})}}={\frac {\Omega _{R}(s_{1})}{\Omega _{R}(s_{2})}}.}$

Так как энтропия резервуара , то вышесказанное становится ${\displaystyle \;S_{R}=k\ln \Omega _{R}}$

${\displaystyle {\frac {P(s_{1})}{P(s_{2})}}={\frac {e^{S_{R}(s_{1})/k}}{e^{S_{R}(s_{2})/k}}}=e^{(S_{R}(s_{1})-S_{R}(s_{2}))/k}.}$

Далее вспомним термодинамическое тождество (из первого закона термодинамики ):

${\displaystyle dS_{R}={\frac {1}{T}}(dU_{R}+P\,dV_{R}-\mu \,dN_{R}).}$

В каноническом ансамбле нет обмена частицами, поэтому член равен нулю. Аналогично, Это дает ${\displaystyle dN_{R}}$ ${\displaystyle dV_{R}=0.}$

${\displaystyle S_{R}(s_{1})-S_{R}(s_{2})={\frac {1}{T}}(U_{R}(s_{1})-U_{R}(s_{2}))=-{\frac {1}{T}}(E(s_{1})-E(s_{2})),}$

где и обозначают энергии резервуара и системы при , соответственно. Для второго равенства мы воспользовались законом сохранения энергии. Подставляя в первое уравнение, связывающее : ${\displaystyle U_{R}(s_{i})}$ ${\displaystyle E(s_{i})}$ ${\displaystyle s_{i}}$ ${\displaystyle P(s_{1}),\;P(s_{2})}$

${\displaystyle {\frac {P(s_{1})}{P(s_{2})}}={\frac {e^{-E(s_{1})/kT}}{e^{-E(s_{2})/kT}}},}$

что подразумевает, для любого состояния s системы

${\displaystyle P(s)={\frac {1}{Z}}e^{-E(s)/kT},}$

где Z — это соответствующим образом выбранная «константа», чтобы сделать общую вероятность равной 1. ( Z является константой при условии, что температура T остается неизменной.)

${\displaystyle Z=\sum _{s}e^{-E(s)/kT},}$

где индекс s пробегает все микросостояния системы. Z иногда называют суммой Больцмана по состояниям (или "Zustandssumme" в оригинальном немецком языке). Если мы индексируем суммирование через собственные значения энергии вместо всех возможных состояний, вырождение должно быть принято во внимание. Вероятность того, что наша система имеет энергию, является просто суммой вероятностей всех соответствующих микросостояний: ${\displaystyle \varepsilon _{i}}$

${\displaystyle P(\varepsilon _{i})={\frac {1}{Z}}g_{i}e^{-\varepsilon _{i}/kT}}$

где, с очевидными изменениями,

${\displaystyle Z=\sum _{j}g_{j}e^{-\varepsilon _{j}/kT},}$

это тот же результат, что и раньше.

Комментарии к этому выводу:

• Обратите внимание, что в этой формулировке изначальное предположение "... предположим, что система имеет всего N частиц ..." опущено. Действительно, количество частиц, имеющихся в системе, не играет никакой роли в достижении распределения. Скорее, то, сколько частиц будут занимать состояния с энергией, следует как простое следствие. ${\displaystyle \varepsilon _{i}}$
• Представленное выше по сути является выводом канонической статистической суммы. Как можно видеть, сравнивая определения, сумма Больцмана по состояниям равна канонической статистической сумме.
• Точно такой же подход можно использовать для вывода статистик Ферми–Дирака и Бозе–Эйнштейна . Однако, там можно заменить канонический ансамбль на большой канонический ансамбль , поскольку между системой и резервуаром происходит обмен частицами. Кроме того, рассматриваемая в этих случаях система является состоянием одной частицы , а не частицей. (В приведенном выше обсуждении мы могли бы предположить, что наша система представляет собой один атом.)

Смотрите также

• Статистика Бозе-Эйнштейна
• Статистика Ферми-Дирака
• фактор Больцмана

Примечания

1. Например, две простые точечные частицы могут иметь одинаковую энергию, но разные векторы импульса. Они могут быть различимы друг от друга на этой основе, и вырождение будет числом возможных способов, которыми они могут быть различены.

Ссылки

1. Толмен, RC (1938). Принципы статистической механики . Dover Publications . ISBN 9780486638966.

Библиография

• Картер, Эшли Х., «Классическая и статистическая термодинамика», Prentice–Hall, Inc., 2001, Нью-Джерси.
• Радж Патриа , «Статистическая механика», Баттерворт–Хайнеманн, 1996.