В дискретной геометрии и механике структурная жесткость представляет собой комбинаторную теорию для прогнозирования гибкости ансамблей, образованных жесткими телами, соединенными гибкими связями или шарнирами .
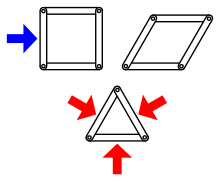
Жесткость — это свойство конструкции, которое заключается в том, что она не сгибается и не прогибается под действием приложенной силы. Противоположностью жесткости является гибкость . В теории структурной жесткости конструкции образуются наборами объектов, которые сами по себе являются жесткими телами, часто предполагаемыми как принимающие простые геометрические формы, такие как прямые стержни (отрезки линий), с парами объектов, соединенных гибкими шарнирами. Конструкция является жесткой, если она не может сгибаться; то есть если нет непрерывного движения конструкции, которое сохраняет форму ее жестких компонентов и схему их соединений в шарнирах.
Существует два принципиально разных вида жесткости. Конечная или макроскопическая жесткость означает, что структура не будет изгибаться, складываться или сгибаться на положительную величину. Бесконечно малая жесткость означает, что структура не будет изгибаться даже на величину, которая слишком мала, чтобы быть обнаруженной даже в теории. (Технически это означает, что некоторые дифференциальные уравнения не имеют ненулевых решений.) Важность конечной жесткости очевидна, но бесконечно малая жесткость также имеет решающее значение, поскольку бесконечно малая гибкость в теории соответствует реальному незначительному изгибу и последующему ухудшению структуры.
Жесткий граф — это вложение графа в евклидово пространство , которое является структурно жестким. [1] То есть граф является жестким, если структура, образованная заменой ребер жесткими стержнями, а вершин гибкими шарнирами, является жесткой. Граф, который не является жестким, называется гибким . Более формально, вложение графа является гибким, если вершины можно перемещать непрерывно, сохраняя расстояния между соседними вершинами, в результате чего расстояния между некоторыми несмежными вершинами изменяются. [2] Последнее условие исключает евклидовы конгруэнтности, такие как простой перенос и поворот.
Также можно рассматривать проблемы жесткости для графов, в которых некоторые ребра представляют собой элементы сжатия (способные растягиваться до большей длины, но не сжиматься до меньшей длины), а другие ребра представляют собой элементы растяжения (способные сжиматься, но не растягиваться). Жесткий граф с ребрами этих типов образует математическую модель структуры тенсегрити .

Основная проблема заключается в том, как предсказать жесткость конструкции с помощью теоретического анализа, не строя ее. Основные результаты в этой области включают следующее:
Однако во многих других простых ситуациях пока не всегда известно, как математически проанализировать жесткость конструкции, несмотря на существование значительной математической теории.
Одним из основателей математической теории структурной жесткости был физик Джеймс Клерк Максвелл . В конце двадцатого века произошел расцвет математической теории жесткости, который продолжается и в двадцать первом веке.
«[A] теория равновесия и прогибов каркасов, подверженных действию сил, действует на твердость качества... в случаях, когда каркас... усилен дополнительными соединительными деталями... в случаях трех измерений, по обычному методу уравнений сил, каждая точка будет иметь три уравнения для определения ее равновесия, так что получится 3 s уравнений между e неизвестными величинами, если s — число точек, а e — число связей[sic]. Однако существует шесть уравнений равновесия системы, которые должны быть обязательно выполнены силами из-за равенства действия и противодействия в каждой части. Следовательно, если e = 3 s − 6, эффект любой вечной силы будет определенным в создании напряжений или давлений в различных частях; но если e > 3 s − 6, эти силы будут неопределенными...» [5]