Евклидово пространство

Фундаментальное пространство геометрии

Точку в трехмерном евклидовом пространстве можно определить по трем координатам.

Евклидово пространство — это фундаментальное пространство геометрии , предназначенное для представления физического пространства . Первоначально, в «Началах » Евклида , это было трехмерное пространство евклидовой геометрии , но в современной математике существуют евклидовы пространства любой положительной целой размерности n , которые называются евклидовыми n -пространствами , когда требуется указать их размерность. ^[1] Для n, равного одному или двум, их обычно называют соответственно евклидовыми прямыми и евклидовыми плоскостями . Квалификатор «евклидов» используется для отличия евклидовых пространств от других пространств , которые позже рассматривались в физике и современной математике.

Древнегреческие геометры ввели евклидово пространство для моделирования физического пространства. Их работа была собрана древнегреческим математиком Евклидом в его «Началах » ^[2] с великим новшеством доказательства всех свойств пространства как теорем , начиная с нескольких фундаментальных свойств, называемых постулатами , которые либо считались очевидными (например, через две точки проходит ровно одна прямая ), либо казались невозможными для доказательства ( постулат о параллельности ).

После введения в конце 19 века неевклидовых геометрий старые постулаты были переформализованы для определения евклидовых пространств через аксиоматическую теорию . Было показано, что другое определение евклидовых пространств с помощью векторных пространств и линейной алгебры эквивалентно аксиоматическому определению. Именно это определение чаще используется в современной математике и подробно изложено в этой статье. ^[3] Во всех определениях евклидовы пространства состоят из точек, которые определяются только свойствами, которыми они должны обладать для формирования евклидова пространства.

По сути, существует только одно евклидово пространство каждого измерения; то есть все евклидовы пространства заданного измерения изоморфны . Поэтому обычно можно работать с определенным евклидовым пространством, обозначаемым или , которое может быть представлено с использованием декартовых координат как действительное n -пространство, снабженное стандартным скалярным произведением . ${\displaystyle \mathbf {E} ^{n}}$ ${\displaystyle \mathbb {E} ^{n}}$ ${\displaystyle \mathbb {R} ^{n}}$

Определение

История определения

Евклидово пространство было введено древними греками как абстракция нашего физического пространства. Их великое новшество, появившееся в «Началах» Евклида, состояло в построении и доказательстве всей геометрии, начиная с нескольких очень базовых свойств, которые абстрагированы от физического мира и не могут быть математически доказаны из-за отсутствия более базовых инструментов. Эти свойства называются постулатами , или аксиомами на современном языке. Этот способ определения евклидова пространства до сих пор используется под названием синтетической геометрии .

В 1637 году Рене Декарт ввел декартовы координаты и показал, что они позволяют сводить геометрические проблемы к алгебраическим вычислениям с числами. Это сведение геометрии к алгебре было серьезным изменением точки зрения, поскольку до этого действительные числа определялись через длины и расстояния.

Евклидова геометрия не применялась в пространствах размерности больше трех до 19 века. Людвиг Шлефли обобщил евклидову геометрию на пространства размерности n , используя как синтетические, так и алгебраические методы, и открыл все правильные многогранники (аналоги Платоновых тел более высокой размерности ), которые существуют в евклидовых пространствах любой размерности. ^[4]

Несмотря на широкое использование подхода Декарта, который назывался аналитической геометрией , определение евклидова пространства оставалось неизменным до конца 19 века. Введение абстрактных векторных пространств позволило использовать их для определения евклидовых пространств с чисто алгебраическим определением. Было показано, что это новое определение эквивалентно классическому определению в терминах геометрических аксиом. Именно это алгебраическое определение в настоящее время чаще всего используется для введения евклидовых пространств.

Мотивация современного определения

Один из способов думать о евклидовой плоскости — это как о наборе точек , удовлетворяющих определенным отношениям, выражаемым в терминах расстояния и углов. Например, на плоскости есть две основные операции (называемые движениями ). Одна из них — это перенос , что означает сдвиг плоскости таким образом, что каждая точка смещается в том же направлении и на то же расстояние. Другая — это вращение вокруг фиксированной точки на плоскости, при котором все точки на плоскости поворачиваются вокруг этой фиксированной точки на тот же угол. Один из основных принципов евклидовой геометрии заключается в том, что две фигуры (обычно рассматриваемые как подмножества ) плоскости следует считать эквивалентными ( конгруэнтными ), если одну из них можно преобразовать в другую с помощью некоторой последовательности переносов, вращений и отражений (см. ниже).

Чтобы сделать все это математически точным, теория должна четко определить, что такое евклидово пространство, и связанные с ним понятия расстояния, угла, переноса и вращения. Даже при использовании в физических теориях евклидово пространство является абстракцией, отделенной от реальных физических местоположений, конкретных систем отсчета , измерительных приборов и т. д. Чисто математическое определение евклидова пространства также игнорирует вопросы единиц длины и других физических измерений : расстояние в «математическом» пространстве — это число , а не что-то выраженное в дюймах или метрах.

Стандартный способ математического определения евклидова пространства, как это делается в оставшейся части этой статьи, — это набор точек, на которые действует реальное векторное пространство — пространство переносов , снабженное скалярным произведением . ^[1] Действие переносов делает пространство аффинным пространством , и это позволяет определять линии, плоскости, подпространства, размерность и параллельность . Сквозное произведение позволяет определять расстояние и углы.

Множество n -кортежей действительных чисел, снабженное скалярным произведением, является евклидовым пространством размерности n . Наоборот, выбор точки, называемой началом координат , и ортонормированного базиса пространства трансляций эквивалентен определению изоморфизма между евклидовым пространством размерности n и рассматриваемым как евклидово пространство. ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle \mathbb {R} ^{n}}$

Отсюда следует, что все , что можно сказать о евклидовом пространстве, можно сказать и о Поэтому многие авторы, особенно на элементарном уровне, называют стандартное евклидово пространство размерности n ^[5] или просто евклидово пространство размерности n . ${\displaystyle \mathbb {R} ^{n}.}$ ${\displaystyle \mathbb {R} ^{n}}$

Иллюстрация евклидовой плоскости, свободная от исходных данных

Причина введения столь абстрактного определения евклидовых пространств и работы с вместо заключается в том, что часто предпочтительнее работать в режиме , свободном от координат и начал (то есть, не выбирая предпочтительный базис и предпочтительное начало). Другая причина заключается в том, что в физическом мире нет стандартного начала и какого-либо стандартного базиса. ${\displaystyle \mathbb {E} ^{n}}$ ${\displaystyle \mathbb {R} ^{n}}$

Техническое определение

АЕвклидово векторное пространство — это конечномерноепространство скалярного произведениянаддействительными числами.^[6]

Евклидово пространство — это аффинное пространство над вещественными числами, такое, что ассоциированное векторное пространство является евклидовым векторным пространством. Евклидовы пространства иногда называют евклидовыми аффинными пространствами, чтобы отличать их от евклидовых векторных пространств. ^[6]

Если E — евклидово пространство, то его связанное векторное пространство (евклидово векторное пространство) часто обозначается Размерностью евклидова пространства является размерность его связанного векторного пространства . ${\displaystyle {\overrightarrow {E}}.}$

Элементы E называются точками и обычно обозначаются заглавными буквами. Элементы называются евклидовыми векторами или свободными векторами . Их также называют переносами , хотя, строго говоря, перенос — это геометрическое преобразование, возникающее в результате действия евклидова вектора на евклидово пространство. ${\displaystyle {\overrightarrow {E}}}$

Действие переноса v на точку P дает точку, которая обозначается P + v . Это действие удовлетворяет

$${\displaystyle P+(v+w)=(P+v)+w.}$$

Примечание: Второй + в левой части — это векторное сложение; каждый другой + обозначает действие вектора на точку. Эта нотация не является двусмысленной, поскольку для различения двух значений + достаточно взглянуть на природу его левого аргумента.

Тот факт, что действие свободно и транзитивно, означает, что для каждой пары точек ( P , Q ) существует ровно один вектор смещения v такой, что P + v = Q. Этот вектор v обозначается Q − P или ${\displaystyle {\overrightarrow {PQ}}{\vphantom {\frac {)}{}}}.}$

Как объяснялось ранее, некоторые из основных свойств евклидовых пространств вытекают из структуры аффинного пространства. Они описаны в § Аффинная структура и его подразделах. Свойства, вытекающие из скалярного произведения, описаны в § Метрическая структура и его подразделах.

Прототипные примеры

Для любого векторного пространства сложение действует свободно и транзитивно на само векторное пространство. Таким образом, евклидово векторное пространство можно рассматривать как евклидово пространство, которое само является ассоциированным векторным пространством.

Типичный случай евклидова векторного пространства рассматривается как векторное пространство, снабженное скалярным произведением в качестве внутреннего произведения . Важность этого конкретного примера евклидова пространства заключается в том, что каждое евклидово пространство изоморфно ему . Точнее, если задано евклидово пространство E размерности n , выбор точки, называемой началом координат , и ортонормированного базиса определяет изоморфизм евклидовых пространств из E в ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle {\overrightarrow {E}}}$ ${\displaystyle \mathbb {R} ^{n}.}$

Поскольку каждое евклидово пространство размерности n изоморфно ему, евклидово пространство иногда называют стандартным евклидовым пространством размерности n . ^[5] ${\displaystyle \mathbb {R} ^{n}}$

Аффинная структура

Некоторые основные свойства евклидовых пространств зависят только от того факта, что евклидово пространство является аффинным пространством . Они называются аффинными свойствами и включают в себя понятия прямых, подпространств и параллельности, которые подробно описаны в следующих подразделах.

Подпространства

Пусть E — евклидово пространство и связанное с ним векторное пространство. ${\displaystyle {\overrightarrow {E}}}$

Плоское евклидово подпространство или аффинное подпространство E — это подмножество F пространства E , такое что

$${\displaystyle {\overrightarrow {F}}={\Bigl \{}{\overrightarrow {PQ}}\mathrel {\Big |} P\in F,Q\in F{\Bigr \}}{\vphantom {\frac {(}{}}}}$$

поскольку ассоциированное векторное пространство F является линейным подпространством (векторным подпространством) A евклидово подпространство F является евклидовым пространством с ассоциированным векторным пространством. Это линейное подпространство также называется направлением F . ${\displaystyle {\overrightarrow {E}}.}$ ${\displaystyle {\overrightarrow {F}}}$ ${\displaystyle {\overrightarrow {F}}}$

Если P — точка F , то

$${\displaystyle F={\Bigl \{}P+v\mathrel {\Big |} v\in {\overrightarrow {F}}{\Bigr \}}.}$$

Наоборот, если P является точкой E и является линейным подпространством , то ${\displaystyle {\overrightarrow {V}}}$ ${\displaystyle {\overrightarrow {E}},}$

$${\displaystyle P+{\overrightarrow {V}}={\Bigl \{}P+v\mathrel {\Big |} v\in {\overrightarrow {V}}{\Bigr \}}}$$

является евклидовым подпространством направления . (Соответствующее векторное пространство этого подпространства — .) ${\displaystyle {\overrightarrow {V}}}$ ${\displaystyle {\overrightarrow {V}}}$

Евклидово векторное пространство (то есть евклидово пространство, равное ) имеет два вида подпространств: его евклидовы подпространства и его линейные подпространства. Линейные подпространства являются евклидовыми подпространствами, а евклидово подпространство является линейным подпространством тогда и только тогда, когда оно содержит нулевой вектор. ${\displaystyle {\overrightarrow {E}}}$ ${\displaystyle {\overrightarrow {E}}}$

Линии и сегменты

В евклидовом пространстве линия — это евклидово подпространство размерности один. Поскольку векторное пространство размерности один охватывается любым ненулевым вектором, линия — это множество вида

$${\displaystyle {\Bigl \{}P+\lambda {\overrightarrow {PQ}}\mathrel {\Big |} \lambda \in \mathbb {R} {\Bigr \}},{\vphantom {\frac {(}{}}}}$$

где P и Q — две различные точки евклидова пространства как части прямой.

Из этого следует, что существует ровно одна прямая, которая проходит через (содержит) две различные точки. Это подразумевает, что две различные прямые пересекаются не более чем в одной точке.

Более симметричное представление линии, проходящей через P и Q, имеет вид

$${\displaystyle {\Bigl \{}O+(1-\lambda ){\overrightarrow {OP}}+\lambda {\overrightarrow {OQ}}\mathrel {\Big |} \lambda \in \mathbb {R} {\Bigr \}},{\vphantom {\frac {(}{}}}}$$

где O — произвольная точка (не обязательно на прямой).

В евклидовом векторном пространстве нулевой вектор обычно выбирается для O ; это позволяет упростить предыдущую формулу до

$${\displaystyle {\bigl \{}(1-\lambda )P+\lambda Q\mathrel {\big |} \lambda \in \mathbb {R} {\bigr \}}.}$$

Стандартное соглашение позволяет использовать эту формулу в любом евклидовом пространстве, см. Аффинное пространство § Аффинные комбинации и барицентр .

Отрезок прямой или просто отрезок , соединяющий точки P и Q, представляет собой подмножество точек, таких, что в предыдущих формулах 0 ≤ 𝜆 ≤ 1. Он обозначается PQ или QP ; то есть

$${\displaystyle PQ=QP={\Bigl \{}P+\lambda {\overrightarrow {PQ}}\mathrel {\Big |} 0\leq \lambda \leq 1{\Bigr \}}.{\vphantom {\frac {(}{}}}}$$

Параллелизм

Два подпространства S и T одинаковой размерности в евклидовом пространстве параллельны , если они имеют одинаковое направление (т.е. одно и то же связанное векторное пространство). ^[a] Эквивалентно, они параллельны, если существует вектор переноса v , который отображает одно в другое:

$${\displaystyle T=S+v.}$$

Для данной точки P и подпространства S существует ровно одно подпространство, содержащее P и параллельное S , то есть В случае, когда S — прямая (подпространство размерности один), это свойство является аксиомой Плейфера . ${\displaystyle P+{\overrightarrow {S}}.}$

Отсюда следует, что на евклидовой плоскости две прямые либо пересекаются в одной точке, либо параллельны.

Концепция параллельных подпространств была распространена на подпространства разных размерностей: два подпространства параллельны, если направление одного из них содержится в направлении другого.

Метрическая структура

Вектор пространства, ассоциированный с евклидовым пространством E, является пространством внутреннего произведения . Это подразумевает симметричную билинейную форму ${\displaystyle {\overrightarrow {E}}}$

$${\displaystyle {\begin{aligned}{\overrightarrow {E}}\times {\overrightarrow {E}}&\to \mathbb {R} \\(x,y)&\mapsto \langle x,y\rangle \end{aligned}}}$$

которая положительно определена (то есть всегда положительна при x ≠ 0 ). ${\displaystyle \langle x,x\rangle }$

Скалярное произведение евклидова пространства часто называют скалярным произведением и обозначают x ⋅ y . Это особенно актуально, когда выбрана декартова система координат , поскольку в этом случае скалярное произведение двух векторов является скалярным произведением их координатных векторов . По этой причине и по историческим причинам для скалярного произведения евклидовых пространств чаще используется точечная нотация, чем скобочная. В этой статье будет использоваться это обозначение; то есть в оставшейся части статьи оно будет обозначаться как x ⋅ y . ${\displaystyle \langle x,y\rangle }$

Евклидова норма вектора x равна

$${\displaystyle \|x\|={\sqrt {x\cdot x}}.}$$

Скалярное произведение и норма позволяют выразить и доказать метрические и топологические свойства евклидовой геометрии . Следующий подраздел описывает наиболее фундаментальные из них. В этих подразделах E обозначает произвольное евклидово пространство, а обозначает его векторное пространство трансляций. ${\displaystyle {\overrightarrow {E}}}$

Расстояние и длина

Расстояние (точнее, евклидово расстояние ) между двумя точками евклидова пространства — это норма вектора переноса, который отображает одну точку в другую; то есть

$${\displaystyle d(P,Q)={\Bigl \|}{\overrightarrow {PQ}}{\Bigr \|}.{\vphantom {\frac {(}{}}}}$$

Длина отрезка PQ — это расстояние d ( P , Q ) между его конечными точками P и Q . Его часто обозначают . ${\displaystyle |PQ|}$

Расстояние является метрикой , поскольку оно положительно определено, симметрично и удовлетворяет неравенству треугольника

$${\displaystyle d(P,Q)\leq d(P,R)+d(R,Q).}$$

Более того, равенство верно тогда и только тогда, когда точка R принадлежит отрезку PQ . Это неравенство означает, что длина любого ребра треугольника меньше суммы длин других ребер. Отсюда и происходит термин неравенство треугольника .

С учетом евклидова расстояния каждое евклидово пространство является полным метрическим пространством .

Ортогональность

Два ненулевых вектора u и v ( соответствующего векторного пространства евклидова пространства E ) перпендикулярны или ортогональны, если их скалярное произведение равно нулю: ${\displaystyle {\overrightarrow {E}}}$

$${\displaystyle u\cdot v=0}$$

Два линейных подпространства ортогональны, если каждый ненулевой вектор первого перпендикулярен каждому ненулевому вектору второго. Это означает, что пересечение линейных подпространств сводится к нулевому вектору. ${\displaystyle {\overrightarrow {E}}}$

Две прямые, и в более общем смысле два евклидовых подпространства (прямую можно рассматривать как одно евклидово подпространство) ортогональны, если их направления (соответствующие векторные пространства евклидовых подпространств) ортогональны. Две ортогональные прямые, которые пересекаются, называются перпендикулярными .

Два отрезка AB и AC , имеющие общую конечную точку A, перпендикулярны или образуют прямой угол, если векторы и ортогональны. ${\displaystyle {\overrightarrow {AB}}{\vphantom {\frac {)}{}}}}$ ${\displaystyle {\overrightarrow {AC}}{\vphantom {\frac {)}{}}}}$

Если AB и AC образуют прямой угол, то

$${\displaystyle |BC|^{2}=|AB|^{2}+|AC|^{2}.}$$

Это теорема Пифагора . Ее доказательство в этом контексте просто, поскольку, выражая это в терминах скалярного произведения, имеем, используя билинейность и симметрию скалярного произведения:

$${\displaystyle {\begin{aligned}|BC|^{2}&={\overrightarrow {BC}}\cdot {\overrightarrow {BC}}{\vphantom {\frac {(}{}}}\\[2mu]&={\Bigl (}{\overrightarrow {BA}}+{\overrightarrow {AC}}{\Bigr )}\cdot {\Bigl (}{\overrightarrow {BA}}+{\overrightarrow {AC}}{\Bigr )}\\[4mu]&={\overrightarrow {BA}}\cdot {\overrightarrow {BA}}+{\overrightarrow {AC}}\cdot {\overrightarrow {AC}}-2{\overrightarrow {AB}}\cdot {\overrightarrow {AC}}\\[6mu]&={\overrightarrow {AB}}\cdot {\overrightarrow {AB}}+{\overrightarrow {AC}}\cdot {\overrightarrow {AC}}\\[6mu]&=|AB|^{2}+|AC|^{2}.\end{aligned}}}$$

Здесь используется , поскольку эти два вектора ортогональны. ${\displaystyle {\overrightarrow {AB}}\cdot {\overrightarrow {AC}}=0{\vphantom {\frac {(}{}}}}$

Угол

Положительные и отрицательные углы на ориентированной плоскости

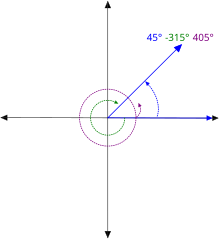
(Неориентированный) угол θ между двумя ненулевыми векторами x и y равен ${\displaystyle {\overrightarrow {E}}}$

$${\displaystyle \theta =\arccos \left({\frac {x\cdot y}{|x|\,|y|}}\right)}$$

где arccos — главное значение функции арккосинуса . По неравенству Коши–Шварца аргумент арккосинуса находится в интервале [−1, 1] . Поэтому θ — вещественное число, и 0 ≤ θ ≤ π (или 0 ≤ θ ≤ 180 , если углы измеряются в градусах).

Углы бесполезны в евклидовой линии, поскольку они могут быть только 0 или π .

В ориентированной евклидовой плоскости можно определить ориентированный угол двух векторов. Ориентированный угол двух векторов x и y тогда противоположен ориентированному углу y и x . В этом случае угол двух векторов может иметь любое значение по модулю целого числа, кратного 2 π . В частности, рефлекторный угол π < θ < 2 π равен отрицательному углу − π < θ − 2 π < 0 .

Угол двух векторов не изменится, если их умножить на положительные числа. Точнее, если x и y — два вектора, а λ и μ — действительные числа, то

$${\displaystyle \operatorname {angle} (\lambda x,\mu y)={\begin{cases}\operatorname {angle} (x,y)\qquad \qquad {\text{if }}\lambda {\text{ and }}\mu {\text{ have the same sign}}\\\pi -\operatorname {angle} (x,y)\qquad {\text{otherwise}}.\end{cases}}}$$

Если A , B , и C являются тремя точками в евклидовом пространстве, угол отрезков AB и AC является углом векторов и Поскольку умножение векторов на положительные числа не меняет угол, угол двух полупрямых с начальной точкой A может быть определен: это угол отрезков AB и AC , где B и C являются произвольными точками, по одной на каждой полупрямой. Хотя это используется реже, можно определить аналогичным образом угол отрезков или полупрямых, которые не имеют общей начальной точки. ${\displaystyle {\overrightarrow {AB}}{\vphantom {\frac {(}{}}}}$ ${\displaystyle {\overrightarrow {AC}}.{\vphantom {\frac {(}{}}}}$

Угол двух прямых определяется следующим образом. Если θ — угол двух сегментов, по одному на каждой прямой, то угол любых двух других сегментов, по одному на каждой прямой, равен либо θ , либо π − θ . Один из этих углов лежит в интервале [0, π /2] , а другой — в [ π /2, π ] . Неориентированный угол двух прямых — это угол в интервале [0, π /2] . В ориентированной евклидовой плоскости ориентированный угол двух прямых принадлежит интервалу [− π /2, π /2] .

Декартовы координаты

Каждое евклидово векторное пространство имеет ортонормированный базис (фактически, бесконечно много в размерности выше единицы и два в размерности один), который является базисом единичных векторов ( ), которые попарно ортогональны ( для i ≠ j ). Точнее, для любого базиса процесс Грама-Шмидта вычисляет ортонормированный базис таким образом, что для каждого i линейные оболочки и равны . ^[7] ${\displaystyle (e_{1},\dots ,e_{n})}$ ${\displaystyle \|e_{i}\|=1}$ ${\displaystyle e_{i}\cdot e_{j}=0}$ ${\displaystyle (b_{1},\dots ,b_{n}),}$ ${\displaystyle (e_{1},\dots ,e_{i})}$ ${\displaystyle (b_{1},\dots ,b_{i})}$

Для евклидова пространства E декартова система координат представляет собой набор данных, состоящий из ортонормированного базиса и точки E , называемой началом координат и часто обозначаемой O. Декартова система координат позволяет определять декартовы координаты как для E , так и для , следующим образом. ${\displaystyle {\overrightarrow {E}},}$ ${\displaystyle (O,e_{1},\dots ,e_{n})}$ ${\displaystyle {\overrightarrow {E}}}$

Декартовы координаты вектора v из являются коэффициентами v в ортонормированном базисе Например, декартовы координаты вектора в ортонормированном базисе (который может быть назван как условно) в трехмерном евклидовом пространстве равны , если . Поскольку базис ортонормирован, i -й коэффициент равен скалярному произведению ${\displaystyle {\overrightarrow {E}}}$ ${\displaystyle e_{1},\dots ,e_{n}.}$ ${\displaystyle v}$ ${\displaystyle (e_{1},e_{2},e_{3})}$ ${\displaystyle (x,y,z)}$ ${\displaystyle (\alpha _{1},\alpha _{2},\alpha _{3})}$ ${\displaystyle v=\alpha _{1}e_{1}+\alpha _{2}e_{2}+\alpha _{3}e_{3}}$ ${\displaystyle \alpha _{i}}$ ${\displaystyle v\cdot e_{i}.}$

Декартовы координаты точки P вектора E являются декартовыми координатами вектора ${\displaystyle {\overrightarrow {OP}}.{\vphantom {\frac {(}{}}}}$

Другие координаты

3-мерные косые координаты

Поскольку евклидово пространство является аффинным пространством , можно рассмотреть на нем аффинный фрейм , который является тем же самым, что и евклидов фрейм, за исключением того, что базис не обязательно должен быть ортонормальным. Это определяет аффинные координаты , иногда называемые косыми координатами для подчеркивания того, что базисные векторы не являются попарно ортогональными.

Аффинный базис евклидова пространства размерности n — это множество из n + 1 точек, не содержащихся в гиперплоскости. Аффинный базис определяет барицентрические координаты для каждой точки.

Многие другие системы координат могут быть определены на евклидовом пространстве E размерности n следующим образом. Пусть f — гомеоморфизм (или, чаще, диффеоморфизм ) из плотного открытого подмножества E в открытое подмножество Координаты точки x из E являются компонентами f ( x ) . Полярная система координат (размерность 2), а также сферическая и цилиндрическая системы координат (размерность 3) определяются таким образом . ${\displaystyle \mathbb {R} ^{n}.}$

Для точек, находящихся вне области f , координаты иногда могут быть определены как предел координат соседних точек, но эти координаты могут быть определены неоднозначно и не быть непрерывными в окрестности точки. Например, для сферической системы координат долгота не определена на полюсе, а на антимеридиане долгота проходит прерывисто от –180° до +180°.

Этот способ определения координат легко распространяется на другие математические структуры, в частности на многообразия .

Изометрии

Изометрия между двумя метрическими пространствами — это биекция , сохраняющая расстояние, ^[b], то есть

$${\displaystyle d(f(x),f(y))=d(x,y).}$$

В случае евклидова векторного пространства изометрия, отображающая начало координат в начало координат, сохраняет норму

$${\displaystyle \|f(x)\|=\|x\|,}$$

поскольку норма вектора — это его расстояние от нулевого вектора. Она также сохраняет внутренний продукт

$${\displaystyle f(x)\cdot f(y)=x\cdot y,}$$

с

$${\displaystyle x\cdot y={\tfrac {1}{2}}\left(\|x+y\|^{2}-\|x\|^{2}-\|y\|^{2}\right).}$$

Изометрия евклидовых векторных пространств — это линейный изоморфизм . ^{[c] [8]}

Изометрия евклидовых пространств определяет изометрию ассоциированных евклидовых векторных пространств. Это подразумевает, что два изометрических евклидовых пространства имеют одинаковую размерность. Наоборот, если E и F — евклидовы пространства, O ∈ E , O ′ ∈ F , и — изометрия, то отображение, определяемое формулой ${\displaystyle f\colon E\to F}$ ${\displaystyle {\overrightarrow {f}}\colon {\overrightarrow {E}}\to {\overrightarrow {F}}}$ ${\displaystyle {\overrightarrow {f}}\colon {\overrightarrow {E}}\to {\overrightarrow {F}}}$ ${\displaystyle f\colon E\to F}$

$${\displaystyle f(P)=O'+{\overrightarrow {f}}{\Bigl (}{\overrightarrow {OP}}{\Bigr )}{\vphantom {\frac {(}{}}}}$$

является изометрией евклидовых пространств.

Из предыдущих результатов следует, что изометрия евклидовых пространств отображает прямые в прямые и, в более общем смысле, евклидовы подпространства в евклидовы подпространства той же размерности, и что ограничение изометрии на эти подпространства является изометрией этих подпространств.

Изометрия с прототипическими примерами

Если E — евклидово пространство, то его связанное векторное пространство можно рассматривать как евклидово пространство. Каждая точка O ∈ E определяет изометрию евклидовых пространств ${\displaystyle {\overrightarrow {E}}}$

$${\displaystyle P\mapsto {\overrightarrow {OP}},{\vphantom {\frac {(}{}}}}$$

который отображает O в нулевой вектор и имеет тождественность как связанное линейное отображение. Обратная изометрия — это отображение

$${\displaystyle v\mapsto O+v.}$$

Евклидова рамка ⁠ ⁠ ${\displaystyle (O,e_{1},\dots ,e_{n})}$ позволяет определить карту

$${\displaystyle {\begin{aligned}E&\to \mathbb {R} ^{n}\\P&\mapsto {\Bigl (}e_{1}\cdot {\overrightarrow {OP}},\dots ,e_{n}\cdot {\overrightarrow {OP}}{\Bigr )},{\vphantom {\frac {(}{}}}\end{aligned}}}$$

которая является изометрией евклидовых пространств. Обратная изометрия — это

$${\displaystyle {\begin{aligned}\mathbb {R} ^{n}&\to E\\(x_{1}\dots ,x_{n})&\mapsto \left(O+x_{1}e_{1}+\dots +x_{n}e_{n}\right).\end{aligned}}}$$

Это означает, что с точностью до изоморфизма существует ровно одно евклидово пространство данной размерности.

Это оправдывает то, что многие авторы говорят о евклидовом пространстве размерности n . ${\displaystyle \mathbb {R} ^{n}}$

Евклидова группа

Изометрия из евклидова пространства на себя называется евклидовой изометрией , евклидовым преобразованием или жестким преобразованием . Жесткие преобразования евклидова пространства образуют группу (при композиции ), называемую евклидовой группой и часто обозначаемую E( n ) от ISO( n ) .

Простейшие евклидовы преобразования — это переносы

$${\displaystyle P\to P+v.}$$

Они находятся во взаимно однозначном соответствии с векторами. Это причина называть пространство трансляций векторным пространством, связанным с евклидовым пространством. Трансляции образуют нормальную подгруппу евклидовой группы.

Евклидова изометрия f евклидова пространства E определяет линейную изометрию связанного векторного пространства (под линейной изометрией подразумевается изометрия, которая также является линейным отображением ) следующим образом: обозначая через Q – P вектор, если O – произвольная точка E , имеем ${\displaystyle {\overrightarrow {f}}}$ ${\displaystyle {\overrightarrow {PQ}},{\vphantom {\frac {(}{}}}}$

$${\displaystyle {\overrightarrow {f}}{\Bigl (}{\overrightarrow {OP}}{\Bigr )}=f(P)-f(O).{\vphantom {\frac {(}{}}}}$$

Несложно доказать, что это линейное отображение, не зависящее от выбора O.

Отображение представляет собой групповой гомоморфизм из евклидовой группы на группу линейных изометрий, называемую ортогональной группой . Ядром этого гомоморфизма является группа трансляций, показывающая, что она является нормальной подгруппой евклидовой группы. ${\displaystyle f\to {\overrightarrow {f}}}$

Изометрии, фиксирующие заданную точку P, образуют стабилизирующую подгруппу евклидовой группы относительно P. Ограничение на этот стабилизатор вышеуказанного группового гомоморфизма является изоморфизмом. Таким образом, изометрии, фиксирующие заданную точку, образуют группу, изоморфную ортогональной группе.

Пусть P — точка, f — изометрия, а t — перенос, который отображает P в f ( P ) . Изометрия фиксирует P . Таким образом , евклидова группа является полупрямым произведением группы переноса и ортогональной группы. ${\displaystyle g=t^{-1}\circ f}$ ${\displaystyle f=t\circ g,}$

Специальная ортогональная группа — это нормальная подгруппа ортогональной группы, сохраняющая ручность . Это подгруппа индекса два ортогональной группы. Ее обратный образ по гомоморфизму группы — это нормальная подгруппа индекса два евклидовой группы, которая называется специальной евклидовой группой или группой смещения . Ее элементы называются жесткими движениями или смещениями . ${\displaystyle f\to {\overrightarrow {f}}}$

Жесткие движения включают тождественные , трансляционные, вращательные (жесткие движения, фиксирующие по крайней мере одну точку), а также винтовые движения .

Типичными примерами жестких преобразований, не являющихся жесткими движениями, являются отражения , которые являются жесткими преобразованиями, фиксирующими гиперплоскость и не являющимися тождественными. Это также преобразования, состоящие в изменении знака одной координаты в некоторой евклидовой системе отсчета.

Так как специальная евклидова группа является подгруппой индекса два евклидовой группы, то при заданном отражении r каждое жесткое преобразование, которое не является жестким движением, является произведением r и жесткого движения. Скользящее отражение является примером жесткого преобразования, которое не является жестким движением или отражением.

Все группы, рассмотренные в этом разделе, являются группами Ли и алгебраическими группами .

Топология

Евклидово расстояние делает евклидово пространство метрическим пространством , и, таким образом, топологическим пространством . Эта топология называется евклидовой топологией . В случае этой топологии это также топология произведения . ${\displaystyle \mathbb {R} ^{n},}$

Открытые множества — это подмножества, которые содержат открытый шар вокруг каждой своей точки. Другими словами, открытые шары образуют базу топологии .

Топологическая размерность евклидова пространства равна его размерности. Это означает, что евклидовы пространства разных размерностей не гомеоморфны . Более того, теорема об инвариантности области утверждает, что подмножество евклидова пространства открыто (для топологии подпространства ) тогда и только тогда, когда оно гомеоморфно открытому подмножеству евклидова пространства той же размерности.

Евклидовы пространства полны и локально компактны . То есть замкнутое подмножество евклидова пространства компактно, если оно ограничено (то есть содержится в шаре). В частности, замкнутые шары компактны.

Аксиоматические определения

Определение евклидовых пространств, описанное в этой статье, принципиально отличается от определения Евклида . В действительности Евклид не определял пространство формально, поскольку оно мыслилось как описание физического мира, существующего независимо от человеческого разума. Необходимость в формальном определении возникла только в конце 19 века с введением неевклидовых геометрий .

Были использованы два различных подхода. Феликс Клейн предложил определять геометрии через их симметрии . Представление евклидовых пространств, приведенное в этой статье, по сути, исходит из его программы Эрланген , с акцентом на группы трансляций и изометрий.

С другой стороны, Дэвид Гильберт предложил набор аксиом , вдохновлённых постулатами Евклида . Они относятся к синтетической геометрии , поскольку не содержат никаких определений действительных чисел . Позже Г. Д. Биркгоф и Альфред Тарский предложили более простые наборы аксиом, которые используют действительные числа (см. аксиомы Биркгофа и аксиомы Тарского ).

В «Геометрической алгебре » Эмиль Артин доказал, что все эти определения евклидового пространства эквивалентны. ^[9] Довольно легко доказать, что все определения евклидовых пространств удовлетворяют аксиомам Гильберта, и что определения, включающие действительные числа (включая приведенное выше определение), эквивалентны. Сложная часть доказательства Артина заключается в следующем. В аксиомах Гильберта конгруэнтность является отношением эквивалентности на отрезках. Таким образом, можно определить длину отрезка как его класс эквивалентности. Таким образом, нужно доказать, что эта длина удовлетворяет свойствам, которые характеризуют неотрицательные действительные числа. Артин доказал это с помощью аксиом, эквивалентных аксиомам Гильберта.

Использование

Со времен древних греков евклидово пространство использовалось для моделирования форм в физическом мире. Таким образом, оно используется во многих науках , таких как физика , механика и астрономия . Оно также широко используется во всех технических областях, которые связаны с формами, фигурами, местоположением и положением, такими как архитектура , геодезия , топография , навигация , промышленный дизайн или техническое черчение .

Пространство размерностей выше трёх встречается в нескольких современных теориях физики; см. Высшая размерность . Они встречаются также в конфигурационных пространствах физических систем .

Помимо евклидовой геометрии , евклидовы пространства также широко используются в других областях математики. Касательные пространства дифференцируемых многообразий являются евклидовыми векторными пространствами. В более общем смысле, многообразие — это пространство, которое локально аппроксимируется евклидовыми пространствами. Большинство неевклидовых геометрий можно смоделировать с помощью многообразия и вложить в евклидово пространство более высокой размерности. Например, эллиптическое пространство можно смоделировать с помощью эллипсоида . Обычно в евклидовом пространстве представляют математические объекты, которые априори не имеют геометрической природы. Примером среди многих является обычное представление графов .

Другие геометрические пространства

С момента введения в конце 19 века неевклидовых геометрий рассматривалось множество видов пространств, о которых можно проводить геометрические рассуждения так же, как и о евклидовых пространствах. В общем, они разделяют некоторые свойства с евклидовыми пространствами, но также могут иметь свойства, которые могут показаться довольно странными. Некоторые из этих пространств используют евклидову геометрию для своего определения или могут быть смоделированы как подпространства евклидова пространства более высокой размерности. Когда такое пространство определяется геометрическими аксиомами , вложение пространства в евклидово пространство является стандартным способом доказательства непротиворечивости его определения или, точнее, доказательства того, что его теория непротиворечива, если евклидова геометрия непротиворечива (что невозможно доказать).

Аффинное пространство

Евклидово пространство — это аффинное пространство, снабженное метрикой . Аффинные пространства имеют много других применений в математике. В частности, поскольку они определены над любым полем , они позволяют выполнять геометрию в других контекстах.

Как только рассматриваются нелинейные вопросы, обычно полезно рассматривать аффинные пространства над комплексными числами как расширение евклидовых пространств. Например, окружность и прямая всегда имеют две точки пересечения (возможно, не различные) в комплексном аффинном пространстве. Поэтому большая часть алгебраической геометрии строится в комплексных аффинных пространствах и аффинных пространствах над алгебраически замкнутыми полями . Формы, которые изучаются в алгебраической геометрии в этих аффинных пространствах, поэтому называются аффинными алгебраическими многообразиями .

Аффинные пространства над рациональными числами и, в более общем смысле, над алгебраическими числовыми полями обеспечивают связь между (алгебраической) геометрией и теорией чисел . Например, Великую теорему Ферма можно сформулировать так: « кривая Ферма степени выше двух не имеет точек в аффинной плоскости над рациональными числами».

Геометрия в аффинных пространствах над конечными полями также широко изучалась. Например, эллиптические кривые над конечными полями широко используются в криптографии .

Проективное пространство

Первоначально проективные пространства были введены путем добавления « точек на бесконечности » к евклидовым пространствам и, в более общем смысле, к аффинным пространствам, чтобы сделать верным утверждение «две копланарные прямые встречаются ровно в одной точке». Проективное пространство разделяет с евклидовыми и аффинными пространствами свойство изотропности , то есть у пространства нет свойства, позволяющего различать две точки или две прямые. Поэтому обычно используется более изотропное определение, которое заключается в определении проективного пространства как множества векторных прямых в векторном пространстве размерности на единицу больше.

Что касается аффинных пространств, проективные пространства определены над любым полем и являются фундаментальными пространствами алгебраической геометрии .

Неевклидовы геометрии

Неевклидова геометрия обычно относится к геометрическим пространствам, где постулат параллельности ложен. Они включают эллиптическую геометрию , где сумма углов треугольника больше 180°, и гиперболическую геометрию , где эта сумма меньше 180°. Их введение во второй половине 19-го века и доказательство того, что их теория непротиворечива (если евклидова геометрия не противоречива), является одним из парадоксов, которые лежат в основе фундаментального кризиса в математике начала 20-го века и мотивировали систематизацию аксиоматических теорий в математике.

Изогнутые пространства

Многообразие — это пространство , которое в окрестности каждой точки напоминает евклидово пространство. С технической точки зрения многообразие — это топологическое пространство , такое, что каждая точка имеет окрестность , гомеоморфную открытому подмножеству евклидова пространства. Многообразия можно классифицировать по возрастанию степени этого «сходства» на топологические многообразия , дифференцируемые многообразия , гладкие многообразия и аналитические многообразия . Однако ни один из этих типов «сходства» не учитывает расстояния и углы, даже приблизительно.

Расстояния и углы можно определить на гладком многообразии, задав плавно меняющуюся евклидову метрику на касательных пространствах в точках многообразия (таким образом, эти касательные пространства являются евклидовыми векторными пространствами). Это приводит к риманову многообразию . Как правило, в римановом многообразии не существует прямых линий , но их роль играют геодезические , которые являются «кратчайшими путями» между двумя точками. Это позволяет определять расстояния, которые измеряются вдоль геодезических, и углы между геодезическими, которые являются углами их касательных в касательном пространстве в точке их пересечения. Таким образом, римановы многообразия ведут себя локально как изогнутое евклидово пространство.

Евклидовы пространства являются тривиально римановыми многообразиями. Примером, хорошо иллюстрирующим это, является поверхность сферы . В этом случае геодезические являются дугами большого круга , которые в контексте навигации называются ортодромами . В более общем смысле пространства неевклидовых геометрий могут быть реализованы как римановы многообразия.

Псевдоевклидово пространство

Скалярное произведение действительного векторного пространства — это положительно определенная билинейная форма , и поэтому характеризуется положительно определенной квадратичной формой . Псевдоевклидово пространство — это аффинное пространство с ассоциированным действительным векторным пространством, снабженное невырожденной квадратичной формой (которая может быть неопределенной ).

Фундаментальным примером такого пространства является пространство Минковского , которое является пространством-временем специальной теории относительности Эйнштейна . Это четырехмерное пространство, где метрика определяется квадратичной формой

$${\displaystyle x^{2}+y^{2}+z^{2}-t^{2},}$$

где последняя координата ( t ) является временной, а остальные три ( x , y , z ) — пространственными.

Для учета гравитации общая теория относительности использует псевдориманово многообразие , касательными пространствами которого являются пространства Минковского . Кривизна этого многообразия в точке является функцией значения гравитационного поля в этой точке.

Смотрите также

• Математический портал

• Гильбертово пространство , обобщение на бесконечное измерение , используемое в функциональном анализе.
• Позиционное пространство , применение в физике

Сноски

1. Это может зависеть от контекста или автора, является ли подпространство параллельным самому себе.
2. Если условие биекции устранено, то функция, сохраняющая расстояние, обязательно инъективна и является изометрией из своей области определения в свой образ.
3. Доказательство: нужно доказать, что . Для этого достаточно доказать, что квадрат нормы левой части равен нулю. Используя билинейность внутреннего произведения, этот квадрат нормы можно разложить в линейную комбинацию и Поскольку f — изометрия, это дает линейную комбинацию и , которая упрощается до нуля. ${\displaystyle f(\lambda x+\mu y)-\lambda f(x)-\mu f(y)=0}$ ${\displaystyle \|f(x)\|^{2},}$ ${\displaystyle \|f(y)\|^{2},}$ ${\displaystyle f(x)\cdot f(y).}$ ${\displaystyle \|x\|^{2},\|y\|^{2},}$ ${\displaystyle x\cdot y,}$

Ссылки

1. Соломенцев 2001.
2. Болл 1960, стр. 50–62.
3. Бергер 1987.
4. Коксетер 1973.
5. Бергер 1987, Раздел 9.1.
6. Бергер 1987, Глава 9.
7. Антон (1987, стр. 209–215)
8. Бергер 1987, Предложение 9.1.3.
9. Артин 1988.

• Антон, Говард (1987), Элементарная линейная алгебра (5-е изд.), Нью-Йорк: Wiley , ISBN 0-471-84819-0
• Артин, Эмиль (1988) [1957], Геометрическая алгебра , Библиотека классических произведений Wiley, Нью-Йорк: John Wiley & Sons Inc., стр. x+214, doi :10.1002/9781118164518, ISBN 0-471-60839-4, МР  1009557
• Болл, WW Rouse (1960) [1908]. Краткое изложение истории математики (4-е изд.). Dover Publications. ISBN 0-486-20630-0.
• Бергер, Марсель (1987), Геометрия I , Берлин: Springer, ISBN 3-540-11658-3
• Coxeter, HSM (1973) [1948]. Правильные многогранники (3-е изд.). Нью-Йорк: Довер. Шлефли... открыл их до 1853 года — времени, когда Кэли, Грассман и Мёбиус были единственными людьми, которые когда-либо задумывались о возможности геометрии в более чем трех измерениях.
• Соломенцев, Э.Д. (2001) [1994], "Евклидово пространство", Энциклопедия математики , Издательство EMS