Аффинное пространство

В математике аффинное пространство — это геометрическая структура , которая обобщает некоторые свойства евклидовых пространств таким образом, что они независимы от понятий расстояния и меры углов , сохраняя только свойства, связанные с параллельностью и соотношением длин параллельных пространств. отрезки линии . Аффинное пространство — это настройка аффинной геометрии .

Как и в евклидовом пространстве, фундаментальные объекты в аффинном пространстве называются точками , которые можно рассматривать как местоположения в пространстве без какого-либо размера или формы: нульмерные . Через любую пару точек можно провести бесконечную прямую — одномерный набор точек; через любые три точки, не лежащие на одной прямой, можно провести двумерную плоскость ; и вообще через $k + 1$ точку общего положения можно нарисовать $k$ -мерное плоское или аффинное подпространство. Аффинное пространство характеризуется представлением пар параллельных линий, которые лежат в одной плоскости, но никогда не встречаются друг с другом (непараллельные линии в одной плоскости пересекаются в точке). Учитывая любую линию, линия, параллельная ей, может быть проведена через любую точку пространства, и говорят, что класс эквивалентности параллельных линий имеет общее направление .

В отличие от векторов в векторном пространстве , в аффинном пространстве нет выделенной точки, служащей началом координат . Не существует заранее определенной концепции сложения или умножения точек, а также умножения точки на скалярное число. Однако для любого аффинного пространства связанное векторное пространство может быть построено из различий между начальной и конечной точками, которые называются векторами смещения , векторами перемещения или просто перемещениями . ^[1] Аналогично, имеет смысл добавить вектор смещения к точке аффинного пространства, в результате чего новая точка будет перенесена из начальной точки этим вектором. Хотя точки не могут быть произвольно сложены вместе, имеет смысл брать аффинные комбинации точек: взвешенные суммы с числовыми коэффициентами, сумма которых равна 1, что дает еще одну точку. Эти коэффициенты определяют барицентрическую систему координат квартиры через точки.

Любое векторное пространство можно рассматривать как аффинное пространство; это равнозначно «забытию» особой роли нулевого вектора . В этом случае элементы векторного пространства можно рассматривать либо как точки аффинного пространства, либо как векторы смещения или трансляции . Если рассматривать нулевой вектор как точку, он называется началом координат . Добавление фиксированного вектора к элементам линейного подпространства (векторного подпространства) векторного пространства создает аффинное подпространство векторного пространства. Обычно говорят, что это аффинное подпространство было получено путем перемещения (от начала координат) линейного подпространства с помощью вектора перемещения (вектора, добавленного ко всем элементам линейного пространства). В конечных размерностях такое аффинное подпространство является множеством решений неоднородной линейной системы. Векторы смещения этого аффинного пространства являются решениями соответствующей однородной линейной системы, которая является линейным подпространством. Линейные подпространства, напротив, всегда содержат начало векторного пространства.

Размерность аффинного пространства определяется как размерность векторного пространства его переводов. Аффинное пространство размерности один — это аффинная прямая . Аффинное пространство размерности 2 является аффинной плоскостью . Аффинное подпространство размерности $n - 1$ в аффинном пространстве или векторном пространстве размерности $n$ является аффинной гиперплоскостью .

Неофициальное описание

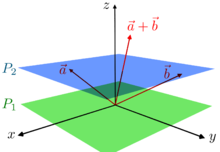
Следующую характеристику, возможно, легче понять, чем обычное формальное определение: аффинное пространство — это то, что осталось от векторного пространства после того, как мы забыли, какая точка является началом координат (или, по словам французского математика Марселя Берже , «аффинное пространство пространство есть не что иное, как векторное пространство, о происхождении которого мы пытаемся забыть, добавляя сдвиги к линейным отображениям» ^[2] ). Представьте, что Алиса знает, что определенная точка является фактическим началом координат, но Боб считает, что другая точка — назовем ее $p$ — является началом координат. Необходимо сложить два вектора $a$ и $b$ . Боб рисует стрелку из точки $p$ в точку $a$ и еще одну стрелку из точки $p$ в точку $b$ и завершает параллелограмм, чтобы найти то, что, по мнению Боба, равно $a + b$ , но Алиса знает, что он на самом деле вычислил

п + (а - п) + (б - п)

Точно так же Алиса и Боб могут оценить любую линейную комбинацию a $и$ b $или$ любого конечного набора векторов и, как правило, получат разные ответы. Однако если сумма коэффициентов линейной комбинации равна 1, то Алиса и Боб придут к одному и тому же ответу.

Если Алиса отправится в

λ а + (1 - λ) б

тогда Боб может аналогичным образом отправиться в

п + λ(а - п) + (1 - λ)(б - п) знак равно λ а + (1 - λ) б

При этом условии для всех коэффициентов $λ + (1 - λ) = 1$ Алиса и Боб описывают одну и ту же точку с одной и той же линейной комбинацией, несмотря на использование разных начал координат.

Хотя только Алиса знает «линейную структуру», и Алиса, и Боб знают «аффинную структуру», то есть значения аффинных комбинаций , определяемых как линейные комбинации, в которых сумма коэффициентов равна 1. Множество с аффинной структурой — это аффинное пространство.

Определение

Хотя аффинное пространство может быть определено аксиоматически (см. § Аксиомы ниже), аналогично определению евклидова пространства, подразумеваемому « Элементами » Евклида , для удобства большинство современных источников определяют аффинные пространства в терминах хорошо развитой теории векторного пространства.

Аффинное пространство — это множество $А$ вместе с векторным пространством и транзитивное и свободное действие аддитивной группы А на множестве $А.$ ^[3] Элементы аффинного пространства $A$ называются точками . Говорят, что векторное пространство связано с аффинным пространством, а его элементы называются векторами , трансляциями или иногда свободными векторами . ${\overrightarrow {A}}$ ${\overrightarrow {A}}$ ${\overrightarrow {A}}$

В явном виде приведенное выше определение означает, что действие представляет собой отображение, обычно обозначаемое как дополнение,

{\begin{aligned}A\times {\overrightarrow {A}}&\to A\\(a,v)\;&\mapsto a+v,\end{aligned}}

который имеет следующие свойства. ^[4]^[5]^[6]

Правильная личность :
$\forall a\in A,\;a+0=a$ , где $0$ — нулевой вектор в ${\overrightarrow {A}}$
Ассоциативность :
$\forall v,w\in {\overrightarrow {A}},\forall a\in A,\;(a+v)+w=a+(v+w)$ (здесь последний $+$ — это добавление в ) ${\overrightarrow {A}}$
Свободное и переходное действие :
Для каждого отображение является биекцией . $a\in A$ ${\overrightarrow {A}}\to A\colon v\mapsto a+v$

Первые два свойства просто определяют свойства (правого) группового действия. Третье свойство характеризует свободные и переходные действия, причем из транзитивности вытекает онтотип , а из свободы действия вытекает инъективный характер. Существует четвертое свойство, вытекающее из пунктов 1, 2 выше:

Наличие индивидуальных переводов

Для всех отображение является биекцией.

v\in {\overrightarrow {A}}

A\to A\colon a\mapsto a+v

Свойство 3 часто используют в следующей эквивалентной форме (5-е свойство).

Вычитание:

Для каждого

a, b

A

существует единственный , обозначаемый

b

-

a

, такой, что .

v\in {\overrightarrow {A}}

b=a+v

Другой способ выразить определение состоит в том, что аффинное пространство — это главное однородное пространство для действия аддитивной группы векторного пространства. Однородные пространства по определению наделены транзитивным групповым действием, а для главного однородного пространства такое транзитивное действие по определению свободно.

Вычитание и аксиомы Вейля

Свойства группового действия позволяют определить вычитание для любой заданной упорядоченной пары $(b, a)$ точек в $A$ , создавая вектор . Этот вектор, обозначенный или , определяется как единственный вектор в таком, что ${\overrightarrow {A}}$ $b-a$ ${\overrightarrow {ab}}$ ${\overrightarrow {A}}$

a+(b-a)=b.

Существование следует из транзитивности действия, а единственность вытекает из того, что действие свободно.

Это вычитание обладает двумя следующими свойствами, называемыми аксиомами Вейля: [ ^7]

$\forall a\in A,\;\forall v\in {\overrightarrow {A}}$ , существует единственная точка такая, что $b\in A$ $b-a=v.$
$\forall a,b,c\in A,\;(c-b)+(b-a)=c-a.$

Свойство параллелограмма выполняется в аффинных пространствах, где оно выражается как: для данных четырех точек равенства и эквивалентны. Это следует из второй аксиомы Вейля, поскольку $a,b,c,d,$ $b-a=d-c$ $c-a=d-b$ $d-a=(d-b)+(b-a)=(d-c)+(c-a).$

Аффинные пространства могут быть эквивалентным образом определены как множество точек $A$ вместе с векторным пространством и вычитанием, удовлетворяющим аксиомам Вейля. В этом случае добавление вектора к точке определяется из первой аксиомы Вейля. ${\overrightarrow {A}}$

Аффинные подпространства и параллелизм

Аффинное подпространство (также называемое в некоторых контекстах линейным многообразием , плоскостью или, над действительными числами , линейным многообразием ) $B$ аффинного пространства $A$ — это подмножество $A$ такое , что для данной точки множество векторы — линейное подпространство . Это свойство, которое не зависит от выбора $a$ , означает, что $B$ является аффинным пространством, которому присвоено векторное пространство. $a\in B$ ${\overrightarrow {B}}=\{b-a\mid b\in B\}$ ${\overrightarrow {A}}$ ${\overrightarrow {B}}$

Аффинные подпространства $A$ - это подмножества $A$ вида

a+V=\{a+w:w\in V\},

где $a$ — точка $A$ , а $V$ — линейное подпространство . ${\overrightarrow {A}}$

Линейное подпространство, связанное с аффинным подпространством, часто называют егонаправлении , а два подпространства, имеющие одно и то же направление, называютсяпараллельными.

Это подразумевает следующее обобщение аксиомы Плейфэра : для любого направления $V$ для любой точки $a$ из $A$ существует одно и только одно аффинное подпространство направления $V$ , которое проходит через a $,$ а именно подпространство $a + V.$

Каждый перевод отображает любое аффинное подпространство в параллельное подпространство. $A\to A:a\mapsto a+v$

Термин «параллель» также используется для обозначения двух аффинных подпространств, направление одного из которых включено в направление другого.

Аффинная карта

Учитывая два аффинных пространства $A$ и $B$ , ассоциированными векторными пространствами которых являются и , аффинное отображение или аффинный гомоморфизм из $A$ в $B$ является отображением. ${\overrightarrow {A}}$ ${\overrightarrow {B}}$

f:A\to B

такой, что

{\begin{aligned}{\overrightarrow {f}}:{\overrightarrow {A}}&\to {\overrightarrow {B}}\\b-a&\mapsto f(b)-f(a)\end{aligned}}

является четко определенным линейным отображением. Под четкостью определения подразумевается, что $b$ $-$ $a$ $=$ $d$ $-$ $c$ подразумевает $f$ $($ $b$ $) -$ $f$ $($ $a$ $) =$ $f$ $($ $d$ $) -$ $f$ $($ $c$ $)$ . $f$

Это означает, что для точки и вектора имеем $a\in A$ $v\in {\overrightarrow {A}}$

f(a+v)=f(a)+{\overrightarrow {f}}(v).

Следовательно, поскольку для любого данного $b$ в $A$ $b = a + v$ для уникального $v$ , $f$ полностью определяется своим значением в одной точке и связанной с ним линейной картой . ${\overrightarrow {f}}$

Эндоморфизмы

Аффинное преобразование или эндоморфизм аффинного пространства — это аффинное отображение этого пространства в себя. Одним из важных семейств примеров являются переводы: для данного вектора карта перевода, которая отправляет каждый вход , является аффинной картой. Другое важное семейство примеров — линейные карты с центром в начале координат: учитывая точку и линейную карту , можно определить аффинную карту с помощью $A$ ${\overrightarrow {v}}$ $T_{\overrightarrow {v}}:A\rightarrow A$ $a\mapsto a+{\overrightarrow {v}}$ $a$ $A$ $b$ $M$ $L_{M,b}:A\rightarrow A$

L_{M,b}(a)=b+M(a-b)

a

A

После выбора источника любая аффинная карта может быть записана однозначно как комбинация перевода и линейной карты с центром в . $b$ $b$

Векторные пространства как аффинные пространства

Каждое векторное пространство $V$ можно рассматривать как аффинное пространство над собой. Это означает, что каждый элемент $V$ можно рассматривать либо как точку, либо как вектор. Это аффинное пространство иногда обозначается $(V, V)$ , чтобы подчеркнуть двойную роль элементов $V.$ Когда нулевой вектор рассматривается как точка, он обычно обозначается $o$ (или $O$ , когда для точек используются заглавные буквы) и называется началом координат .

Если $A$ - другое аффинное пространство над тем же векторным пространством (то есть ), выбор любой точки $a$ в $A$ определяет уникальный аффинный изоморфизм, который является тождественным $V$ и отображает $a$ в $o$ . Другими словами, выбор начала координат $a$ в $A$ позволяет отождествить $A$ и $($ $V$ $,$ $V$ $)$ с точностью до канонического изоморфизма . Противоположностью этого свойства является то, что аффинное пространство $A$ может быть отождествлено с векторным пространством $V$ , в котором «место начала забыто». $V={\overrightarrow {A}}$

Связь с евклидовыми пространствами

Определение евклидовых пространств

Евклидовы пространства (включая одномерную линию, двумерную плоскость и трехмерное пространство, обычно изучаемые в элементарной геометрии, а также многомерные аналоги) являются аффинными пространствами.

Действительно, в большинстве современных определений евклидово пространство определяется как аффинное пространство, такое, что связанное векторное пространство представляет собой вещественное пространство внутреннего произведения конечной размерности, то есть векторное пространство над вещественными числами с положительно определенной квадратичной формой $q. (Икс)$ . Внутренний продукт двух векторов $x$ и $y$ является значением симметричной билинейной формы

x\cdot y={\frac {1}{2}}(q(x+y)-q(x)-q(y)).

Обычное евклидово расстояние между двумя точками $A$ и $B$ равно

d(A,B)={\sqrt {q(B-A)}}.

В более старом определении евклидовых пространств через синтетическую геометрию векторы определяются как классы эквивалентности упорядоченных пар точек при равновесии (пары $(A, B)$ и $(C, D)$ равносильны , если точки $A, B, D, C$ ( именно в таком порядке) образуют параллелограмм . Несложно проверить, что векторы образуют векторное пространство, квадрат евклидова расстояния является квадратичной формой в пространстве векторов, а два определения евклидовых пространств эквивалентны.

Аффинные свойства

В евклидовой геометрии общая фраза « аффинное свойство » относится к свойству, которое можно доказать в аффинных пространствах, то есть его можно доказать без использования квадратичной формы и связанного с ней внутреннего продукта. Другими словами, аффинное свойство — это свойство, не связанное с длинами и углами. Типичными примерами являются параллелизм и определение касательной . Непримером является определение нормального .

Эквивалентно, аффинное свойство — это свойство, которое инвариантно относительно аффинных преобразований евклидова пространства.

Аффинные комбинации и барицентр

Пусть $a 1, ..., an n$ — совокупность из $n$ точек аффинного пространства и n $элементов$ основного поля . $\lambda _{1},\dots ,\lambda _{n}$

Предположим, что . Для любых двух точек $o$ и $o'$ имеется $\lambda _{1}+\dots +\lambda _{n}=0$

\lambda _{1}{\overrightarrow {oa_{1}}}+\dots +\lambda _{n}{\overrightarrow {oa_{n}}}=\lambda _{1}{\overrightarrow {o'a_{1}}}+\dots +\lambda _{n}{\overrightarrow {o'a_{n}}}.

Таким образом, эта сумма не зависит от выбора начала координат, а результирующий вектор можно обозначить

\lambda _{1}a_{1}+\dots +\lambda _{n}a_{n}.

Когда , получают определение вычитания точек. $n=2,\lambda _{1}=1,\lambda _{2}=-1$

Теперь предположим, что элементы поля удовлетворяют . Для некоторого выбора начала координат $o$ обозначим единственную точку такую, что $\lambda _{1}+\dots +\lambda _{n}=1$ $g$

\lambda _{1}{\overrightarrow {oa_{1}}}+\dots +\lambda _{n}{\overrightarrow {oa_{n}}}={\overrightarrow {og}}.

Можно показать, что это не зависит от выбора $o$ . Следовательно, если $g$

\lambda _{1}+\dots +\lambda _{n}=1,

можно написать

g=\lambda _{1}a_{1}+\dots +\lambda _{n}a_{n}.

Точка называется барицентром для весов . Говорят также, что это аффинная комбинация с коэффициентами . $g$ $a_{i}$ $\lambda _{i}$ $g$ $a_{i}$ $\lambda _{i}$

Примеры

Когда дети находят ответы на такие суммы, как $4 + 3$ или $4 - 2$ , считая вправо или влево на числовой прямой , они рассматривают числовую прямую как одномерное аффинное пространство.
Пространство энергий является аффинным пространством для , так как часто не имеет смысла говорить об абсолютной энергии, но имеет смысл говорить об энергетических различиях. Энергия вакуума при ее определении приобретает каноническое происхождение. $\mathbb {R}$
Физическое пространство часто моделируется как аффинное пространство в нерелятивистских и релятивистских условиях. Чтобы отличить их от векторного пространства, их иногда называют евклидовыми пространствами и . $\mathbb {R} ^{3}$ $\mathbb {R} ^{1,3}$ ${\text{E}}(3)$ ${\text{E}}(1,3)$
Любой смежный класс подпространства $V$ векторного пространства является аффинным пространством над этим подпространством.
Если $T$ — матрица и $b$ лежит в пространстве ее столбцов , множество решений уравнения $T x = b$ является аффинным пространством над подпространством решений уравнения $T x = 0$ .
Решения неоднородного линейного дифференциального уравнения образуют аффинное пространство над решениями соответствующего однородного линейного уравнения.
Обобщая все вышесказанное, если $T : V \to W$ — линейное отображение и $y$ лежит в его образе , множество решений $x \in V$ уравнения $T x = y$ является смежным классом ядра $T$ и, следовательно, является аффинное пространство над $Ker T$ .
Пространство (линейных) дополнительных подпространств векторного подпространства $V$ в векторном пространстве $W$ является аффинным пространством над $Hom(W / V, V)$ . То есть, если $0 \to V \to W \to X \to 0$ — короткая точная последовательность векторных пространств, то пространство всех расщеплений точной последовательности естественным образом несет в себе структуру аффинного пространства над $Hom(X, V)$ .
Пространство связностей (если смотреть со стороны векторного расслоения , где – гладкое многообразие ) является аффинным пространством для векторного пространства значных 1-форм . Пространство связностей (если смотреть со стороны главного расслоения ) является аффинным пространством для векторного пространства -значных 1-форм, где – ассоциированное присоединенное расслоение . $E\xrightarrow {\pi } M$ $M$ ${\text{End}}(E)$ $P\xrightarrow {\pi } M$ ${\text{ad}}(P)$ ${\text{ad}}(P)$

Аффинный диапазон и базы

Для любого непустого подмножества $X$ аффинного пространства $A$ существует наименьшее содержащее его аффинное подпространство, называемое аффинной оболочкой $X$ . Это пересечение всех аффинных подпространств, содержащих X $,$ и его направление является пересечением направлений аффинных подпространств, содержащих $X.$

Аффинная оболочка $X$ — это набор всех (конечных) аффинных комбинаций точек X $,$ а ее направление — это $линейная$ оболочка x $-$ $y$ для $x$ и $y$ в $X.$ Если кто-то выбирает конкретную точку $x$ $0$ , направление аффинного промежутка $X$ также является линейным промежутком $x$ $-$ $x$ $0$ для $x$ в $X$ .

Говорят также, что аффинная оболочка $X$ порождается $X$ и что X $является$ порождающим множеством ее аффинной оболочки.

Множество $X$ точек аффинного пространства называетсяаффинно независимый или простонезависимый,если аффинная оболочка любогострогого подмножестваXявляется строгим подмножеством аффинной оболочки $X$ $.$ АнАффинный базис илибарицентрическая рамка(см. § Барицентрические координаты ниже) аффинного пространства представляет собой порождающий набор, который также является независимым (то есть минимальныйпорождающий набор).

Напомним, что размерность аффинного пространства — это размерность связанного с ним векторного пространства. Базисы аффинного пространства конечной размерности $n$ — это независимые подмножества из $n + 1$ элементов или, что то же самое, порождающие подмножества из $n + 1$ элементов. Эквивалентно, ${x 0, ..., x n$ } является аффинным базисом аффинного пространства тогда и только тогда, когда ${x 1 - x 0, ..., x n - x 0$ } является линейным базисом соответствующего вектора. космос.

Координаты

Есть два сильно связанных типа систем координат , которые можно определить в аффинных пространствах.

Барицентрические координаты

Пусть $A$ — аффинное пространство размерности $n$ над полем $k$ и — аффинный базис $A.$ Из свойств аффинного базиса следует, что для каждого $x$ в $A$ существует единственный $($ $n$ $+ 1)$ набор элементов k такой, $что$ $\{x_{0},\dots ,x_{n}\}$ $(\lambda _{0},\dots ,\lambda _{n})$

\lambda _{0}+\dots +\lambda _{n}=1

x=\lambda _{0}x_{0}+\dots +\lambda _{n}x_{n}.

Они называются барицентрическими координатами x над аффинным базисом $.$ Если $xi$ рассматривать как тела, имеющие веса (или массы) , точка $x,$ $таким образом$ $,$ является барицентром xi , $и$ это объясняет происхождение термина барицентрические координаты . $\lambda _{i}$ $\{x_{0},\dots ,x_{n}\}$ $\lambda _{i}$

Барицентрические координаты определяют аффинный изоморфизм между аффинным пространством $A$ и аффинным подпространством $k n + 1$ , определяемым уравнением . $\lambda _{0}+\dots +\lambda _{n}=1$

Для аффинных пространств бесконечной размерности применяется то же определение, но с использованием только конечных сумм. Это означает, что для каждой точки только конечное число координат отличны от нуля.

Аффинные координаты

Аффинный фрейм аффинного пространства состоит из точки, называемой началом координат , и линейного базиса соответствующего векторного пространства. Точнее, для аффинного пространства $A$ с ассоциированным векторным пространством начало $o$ принадлежит $A$ , а линейный базис является базисом ( $v$ $1$ $,$ $...,$ $v$ $n$ $)$ (для простоты обозначений мы рассматриваем только случае конечной размерности, общий случай аналогичен). ${\overrightarrow {A}}$ ${\overrightarrow {A}}$

Для каждой точки $p$ из $A$ существует уникальная последовательность элементов основного поля такая, что $\lambda _{1},\dots ,\lambda _{n}$

p=o+\lambda _{1}v_{1}+\dots +\lambda _{n}v_{n},

или эквивалентно

{\overrightarrow {op}}=\lambda _{1}v_{1}+\dots +\lambda _{n}v_{n}.

Они называются аффинными координатами p $в$ аффинной системе отсчета $($ $o$ $,$ $v1$ $,$ $...$ $,$ $vn$ $)$ . $\lambda _{i}$

Пример: В евклидовой геометрии декартовы координаты — это аффинные координаты относительно ортонормированной системы отсчета , то есть аффинной системы отсчета $(o, v 1, ..., v n)$ , такой что $(v 1, ..., v n)$ является ортонормированный базис .

Связь между барицентрическими и аффинными координатами

Барицентрические координаты и аффинные координаты тесно связаны между собой и могут считаться эквивалентными.

Действительно, в барицентрической системе отсчёта

(x_{0},\dots ,x_{n}),

сразу выводится аффинная система координат

(x_{0},{\overrightarrow {x_{0}x_{1}}},\dots ,{\overrightarrow {x_{0}x_{n}}})=\left(x_{0},x_{1}-x_{0},\dots ,x_{n}-x_{0}\right),

и если

\left(\lambda _{0},\lambda _{1},\dots ,\lambda _{n}\right)

— барицентрические координаты точки в барицентрической системе отсчета, то аффинные координаты той же точки в аффинной системе отсчета равны

\left(\lambda _{1},\dots ,\lambda _{n}\right).

И наоборот, если

\left(o,v_{1},\dots ,v_{n}\right)

является аффинной рамкой, то

\left(o,o+v_{1},\dots ,o+v_{n}\right)

представляет собой барицентрическую систему отсчета. Если

\left(\lambda _{1},\dots ,\lambda _{n}\right)

являются аффинными координатами точки в аффинной системе отсчета, то ее барицентрические координаты в барицентрической системе отсчета равны

\left(1-\lambda _{1}-\dots -\lambda _{n},\lambda _{1},\dots ,\lambda _{n}\right).

Следовательно, барицентрические и аффинные координаты практически эквивалентны. В большинстве приложений предпочтительны аффинные координаты, поскольку они включают меньше независимых координат. Однако в ситуациях, когда важные точки изучаемой задачи аффинно независимы, барицентрические координаты могут привести к более простым вычислениям, как в следующем примере.

Пример треугольника

Вершины неплоского треугольника образуют аффинный базис евклидовой плоскости . Барицентрические координаты позволяют легко охарактеризовать элементы треугольника, не включающие углы или расстояния:

Вершины — это точки барицентрических координат $(1, 0, 0)$ , $(0, 1, 0)$ и $(0, 0, 1)$ . Линии, поддерживающие края, — это точки, имеющие нулевую координату. Сами ребра — это точки, имеющие одну нулевую координату и две неотрицательные координаты. Внутренностью треугольника являются точки, все координаты которых положительны. Медианы — это точки, имеющие две равные координаты, а центроид — это точка координат $($ $.mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output .sfrac.tion,.mw-parser-output .sfrac .tion{display:inline-block;vertical-align:-0.5em;font-size:85%;text-align:center}.mw-parser-output .sfrac .num{display:block;line-height:1em;margin:0.0em 0.1em;border-bottom:1px solid}.mw-parser-output .sfrac .den{display:block;line-height:1em;margin:0.1em 0.1em}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px}1/3,1/3,1/3)$ .

Изменение координат

Случай барицентрических координат

Барицентрические координаты легко меняются от одного базиса к другому. Пусть и – аффинные базы $A$ . Для каждого $x$ в $A$ существует кортеж, для которого $\{x_{0},\dots ,x_{n}\}$ $\{x'_{0},\dots ,x'_{n}\}$ $\{\lambda _{0},\dots ,\lambda _{n}\}$

x=\lambda _{0}x_{0}+\dots +\lambda _{n}x_{n}.

Аналогично, для каждого из первого базиса мы теперь имеем во втором базисе $x_{i}\in \{x_{0},\dots ,x_{n}\}$

x_{i}=\lambda _{i,0}x'_{0}+\dots +\lambda _{i,j}x'_{j}+\dots +\lambda _{i,n}x'_{n}

для некоторого кортежа . Теперь мы можем переписать наше выражение в первом базисе как выражение во втором с помощью $\{\lambda _{i,0},\dots ,\lambda _{i,n}\}$

\,x=\sum _{i=0}^{n}\lambda _{i}x_{i}=\sum _{i=0}^{n}\lambda _{i}\sum _{j=0}^{n}\lambda _{i,j}x'_{j}=\sum _{j=0}^{n}{\biggl (}\sum _{i=0}^{n}\lambda _{i}\lambda _{i,j}{\biggr )}x'_{j}\,,

давая нам координаты во втором базисе в виде кортежа . ${\textstyle {\bigl \{}\sum _{i}\lambda _{i}\lambda _{i,0},\,\dots ,\,{}}$ ${\textstyle \sum _{i}\lambda _{i}\lambda _{i,n}{\bigr \}}}$

Случай аффинных координат

Аффинные координаты также легко переходят из одного базиса в другой. Пусть , и , — аффинные рамки $A$ . Для каждой точки $p$ из $A$ существует уникальная последовательность элементов основного поля такая, что $o$ $\{v_{1},\dots ,v_{n}\}$ $o'$ $\{v'_{1},\dots ,v'_{n}\}$ $\lambda _{1},\dots ,\lambda _{n}$

p=o+\lambda _{1}v_{1}+\dots +\lambda _{n}v_{n},

и аналогично, для каждого из первого базиса мы теперь имеем во втором базисе $v_{i}\in \{v_{1},\dots ,v_{n}\}$

o=o'+\lambda _{o,1}v'_{1}+\dots +\lambda _{o,j}v'_{j}+\dots +\lambda _{o,n}v'_{n}\,

v_{i}=\lambda _{i,1}v'_{1}+\dots +\lambda _{i,j}v'_{j}+\dots +\lambda _{i,n}v'_{n}

для кортежа и кортежей . Теперь мы можем переписать наше выражение в первом базисе как выражение во втором с помощью $\{\lambda _{o,1},\dots ,\lambda _{o,n}\}$ $\{\lambda _{i,1},\dots ,\lambda _{i,n}\}$

{\begin{aligned}\,p&=o+\sum _{i=1}^{n}\lambda _{i}v_{i}={\biggl (}o'+\sum _{j=1}^{n}\lambda _{o,j}v'_{j}{\biggr )}+\sum _{i=1}^{n}\lambda _{i}\sum _{j=1}^{n}\lambda _{i,j}v'_{j}\\&=o'+\sum _{j=1}^{n}{\biggl (}\lambda _{o,j}+\sum _{i=1}^{n}\lambda _{i}\lambda _{i,j}{\biggr )}v'_{j}\,,\end{aligned}}

давая нам координаты во втором базисе в виде кортежа . ${\textstyle {\bigl \{}\lambda _{o,1}+\sum _{i}\lambda _{i}\lambda _{i,1},\,\dots ,\,{}}$ ${\textstyle \lambda _{o,n}+\sum _{i}\lambda _{i}\lambda _{i,n}{\bigr \}}}$

Свойства аффинных гомоморфизмов

Матричное представление

Изображение и волокна

Позволять

f\colon E\to F

— аффинный гомоморфизм, причем

{\overrightarrow {f}}\colon {\overrightarrow {E}}\to {\overrightarrow {F}}

связанная с ним линейная карта. Образ f $—$ это аффинное подпространство F , которому соответствует векторное $пространство$ . Поскольку аффинное пространство не имеет нулевого элемента , аффинный гомоморфизм не имеет ядра . Однако линейное отображение делает это, и если мы обозначим его ядром, то для любой точки $x из , прообраз x$ $является$ аффинным подпространством E , направление $которого$ равно . Это аффинное $подпространство$ называется слоем x . $f(E)=\{f(a)\mid a\in E\}$ ${\overrightarrow {f}}({\overrightarrow {E}})$ ${\overrightarrow {f}}$ $K=\{v\in {\overrightarrow {E}}\mid {\overrightarrow {f}}(v)=0\}$ $f(E)$ $f^{-1}(x)$ $K$

Проекция

Важным примером является проекция, параллельная некоторому направлению, на аффинное подпространство. Важность этого примера заключается в том, что евклидовы пространства являются аффинными пространствами и что такого рода проекции являются фундаментальными в евклидовой геометрии .

Точнее, для данного аффинного пространства $E$ с соответствующим векторным пространством пусть $F$ — аффинное подпространство направления , а $D$ — дополнительное подпространство в (это означает, что каждый вектор может быть разложен уникальным образом как сумма элемента и элемент $D$ ). Для каждой точки $x$ из $E$ ее проекция на $F$ , параллельная $D$ , является единственной точкой $p$ $($ $x$ $)$ в $F$ такой, что ${\overrightarrow {E}}$ ${\overrightarrow {F}}$ ${\overrightarrow {F}}$ ${\overrightarrow {E}}$ ${\overrightarrow {E}}$ ${\overrightarrow {F}}$

p(x)-x\in D.

Это аффинный гомоморфизм, связанное с ним линейное отображение определяется формулой ${\overrightarrow {p}}$

{\overrightarrow {p}}(x-y)=p(x)-p(y),

для $x$ и $y$ в $E$ .

Образ этой проекции — $F$ , а его слои — подпространства направления $D.$

Факторное пространство

Хотя ядра для аффинных пространств не определены, факторпространства определены. Это следует из того, что «принадлежность одному и тому же слою аффинного гомоморфизма» является отношением эквивалентности.

Пусть $E$ — аффинное пространство, а $D$ — линейное подпространство соответствующего векторного пространства . Фактор $E$ $/$ $D$ $E$ по $D$ — это фактор E по отношению эквивалентности такой, что $x$ $и$ y $эквивалентны$ , если ${\overrightarrow {E}}$

x-y\in D.

Этот фактор представляет собой аффинное пространство, которому соответствует векторное пространство. ${\overrightarrow {E}}/D$

Для каждого аффинного гомоморфизма образ изоморфен фактору $E$ по ядру соответствующего линейного отображения. Это первая теорема об изоморфизме аффинных пространств. $E\to F$

Аксиомы

Аффинные пространства обычно изучаются с помощью аналитической геометрии с использованием координат или, что то же самое, векторных пространств. Их также можно изучать как синтетическую геометрию , записывая аксиомы, хотя этот подход встречается гораздо реже. Существует несколько различных систем аксиом аффинного пространства.

Коксетер (1969, стр. 192) аксиоматизирует частный случай аффинной геометрии над вещественными числами как упорядоченную геометрию вместе с аффинной формой теоремы Дезарга и аксиомой, утверждающей, что на плоскости существует не более одной линии, проходящей через данную точку, не пересекающей заданную точку. данную строку.

Аффинные плоскости удовлетворяют следующим аксиомам (Cameron 1991, глава 2): (в которых две прямые называются параллельными, если они равны или не пересекаются):

Любые две различные точки лежат на одной прямой.
Учитывая точку и линию, существует уникальная линия, которая содержит точку и параллельна линии.
Существуют три неколлинеарные точки.

Помимо аффинных плоскостей над полями (или тел ), существует также множество недезарговых плоскостей, удовлетворяющих этим аксиомам. (Кэмерон 1991, глава 3) дает аксиомы для аффинных пространств более высокой размерности.

Чисто аксиоматическая аффинная геометрия является более общей, чем аффинные пространства, и рассматривается в отдельной статье .

Связь с проективными пространствами

Аффинные пространства содержатся в проективных пространствах . Например, аффинную плоскость можно получить из любой проективной плоскости , удалив одну прямую и все точки на ней, и наоборот, любую аффинную плоскость можно использовать для построения проективной плоскости в качестве замыкания, добавив бесконечную линию , точки которой соответствуют классы эквивалентности параллельных прямых . Подобные конструкции справедливы и в более высоких размерностях.

Кроме того, преобразования проективного пространства, сохраняющие аффинное пространство (т. е. оставляющие гиперплоскость на бесконечности инвариантной как множество ), приводят к преобразованиям аффинного пространства. И наоборот, любое аффинное линейное преобразование однозначно расширяется до проективного линейного преобразования , поэтому аффинная группа является подгруппой проективной группы . Например, преобразования Мёбиуса (преобразования комплексной проективной прямой или сферы Римана ) являются аффинными (преобразования комплексной плоскости ) тогда и только тогда, когда они фиксируют точку на бесконечности .

Аффинная алгебраическая геометрия

В алгебраической геометрии аффинное многообразие (или, в более общем плане, аффинное алгебраическое множество ) определяется как подмножество аффинного пространства, которое представляет собой набор общих нулей набора так называемых полиномиальных функций над аффинным пространством . Для определения полиномиальной функции в аффинном пространстве необходимо выбрать аффинную систему координат . Тогда полиномиальная функция — это функция такая, что изображение любой точки является значением некоторой многомерной полиномиальной функции координат точки. Поскольку изменение аффинных координат может быть выражено линейными функциями (точнее, аффинными функциями) координат, это определение не зависит от конкретного выбора координат.

Выбор системы аффинных координат для аффинного пространства размерности $n$ над полем $k$ индуцирует аффинный изоморфизм между и аффинным координатным пространством $k$ $n$ . Это объясняет, почему во многих учебниках для упрощения пишут и вводят аффинные алгебраические многообразия как общие нули полиномиальных функций над $k$ $n$ . ^[8] $\mathbb {A} _{k}^{n}$ $\mathbb {A} _{k}^{n}$ $\mathbb {A} _{k}^{n}=k^{n}$

Поскольку все аффинное пространство представляет собой набор общих нулей нулевого многочлена , аффинные пространства являются аффинными алгебраическими многообразиями.

Кольцо полиномиальных функций

Согласно приведенному выше определению, выбор аффинной рамки аффинного пространства позволяет отождествлять полиномиальные функции с полиномами от $n$ переменных, причем i -я переменная представляет функцию, которая отображает точку в ее $i-$ ю координату. Отсюда следует, что множество полиномиальных функций над является k - алгеброй , обозначаемой , которая изоморфна кольцу многочленов . $\mathbb {A} _{k}^{n}$ $\mathbb {A} _{k}^{n}$ $\mathbb {A} _{k}^{n}$ $k\left[\mathbb {A} _{k}^{n}\right]$ $k\left[X_{1},\dots ,X_{n}\right]$

Когда кто-то меняет координаты, изоморфизм между и изменяется соответственно, и это вызывает автоморфизм , который отображает каждую неопределенную величину в полином первой степени. Отсюда следует, что полная степень определяет фильтрацию , независимую от выбора координат. Общая степень определяет также градуировку , но она зависит от выбора координат, так как изменение аффинных координат может отобразить неопределенные величины на неоднородные многочлены . $k\left[\mathbb {A} _{k}^{n}\right]$ $k[X_{1},\dots ,X_{n}]$ $k\left[X_{1},\dots ,X_{n}\right]$ $k\left[\mathbb {A} _{k}^{n}\right]$

Топология Зариского

Аффинные пространства над топологическими полями , такими как действительные или комплексные числа, имеют естественную топологию . Топология Зарисского, определенная для аффинных пространств над любым полем, в любом случае позволяет использовать топологические методы. Топология Зариского — это единственная топология в аффинном пространстве, замкнутые множества которого представляют собой аффинные алгебраические множества (то есть множества общих нулей полиномиальных функций над аффинным множеством). Поскольку полиномиальные функции над топологическим полем непрерывны, каждое замкнутое множество Зарисского замкнуто для обычной топологии, если таковая имеется. Другими словами, топология Зарисского над топологическим полем грубее естественной топологии.

Существует естественная инъективная функция из аффинного пространства во множество простых идеалов (то есть спектр ) его кольца полиномиальных функций. Когда выбраны аффинные координаты, эта функция отображает точку координат в максимальный идеал . Эта функция является гомеоморфизмом (для топологии Зарисского аффинного пространства и спектра кольца полиномиальных функций) аффинного пространства на образ функции. $\left(a_{1},\dots ,a_{n}\right)$ $\left\langle X_{1}-a_{1},\dots ,X_{n}-a_{n}\right\rangle$

Случай алгебраически замкнутого основного поля особенно важен в алгебраической геометрии, потому что в этом случае приведенный выше гомеоморфизм представляет собой отображение между аффинным пространством и множеством всех максимальных идеалов кольца функций (это Nullstellensatz Гильберта ).

Это исходная идея теории схем Гротендика , которая состоит в том, чтобы при изучении алгебраических многообразий рассматривать в качестве «точек» не только точки аффинного пространства, но и все простые идеалы спектра. Это позволяет склеивать алгебраические многообразия аналогично тому, как для многообразий склеиваются карты для построения многообразия .

Когомологии

Как и все аффинные разновидности, локальные данные в аффинном пространстве всегда можно объединить глобально: когомологии аффинного пространства тривиальны. Точнее, для всех когерентных пучков F и целых чисел . Этим свойством обладают и все остальные родственные сорта . Но также все группы этальных когомологий в аффинном пространстве тривиальны. В частности, каждое линейное расслоение тривиально. В более общем смысле, из теоремы Квиллена–Суслина следует, что каждое алгебраическое векторное расслоение над аффинным пространством тривиально. $H^{i}\left(\mathbb {A} _{k}^{n},\mathbf {F} \right)=0$ $i>0$

Смотрите также

Аффинная оболочка - наименьшее аффинное подпространство, содержащее подмножество.
Комплексное аффинное пространство - Аффинное пространство над комплексными числами.
Экзотическое аффинное пространство - Реальное аффинное пространство четной размерности, не изоморфное комплексному аффинному пространству.
Пространство (математика) - математический набор с некоторой дополнительной структурой.
Барицентрическая система координат

Примечания

^ Слово «перевод» обычно предпочтительнее «вектора смещения» , что может сбивать с толку, поскольку смещения включают также повороты .
^ Бергер 1987, с. 32
^ Бергер, Марсель (1984), «Аффинные пространства», Проблемы геометрии , Springer, стр. 11, ISBN 9780387909714
^ Бергер 1987, с. 33
^ Снаппер, Эрнст; Тройер, Роберт Дж. (1989), Метрическая аффинная геометрия , с. 6
^ Таррида, Агусти Р. (2011), «Аффинные пространства», Аффинные карты, евклидовы движения и квадрики, Springer, стр. 1–2, ISBN 9780857297105
^ Номидзу и Сасаки 1994, с. 7
^ Хартсхорн 1977, гл. Я, § 1.