Сферическая аберрация

Сверху изображена идеальная линза без сферической аберрации: все входящие лучи фокусируются в фокусной точке .
Нижний пример изображает настоящую линзу со сферическими поверхностями, которая создает сферическую аберрацию: различные лучи не встречаются после линзы в одной фокусной точке. Чем дальше лучи от оптической оси , тем ближе к линзе они пересекают оптическую ось (положительная сферическая аберрация).
(Рисунок преувеличен.)

Сферическая аберрация коллимированного света , падающего на вогнутое сферическое зеркало .

Оптическая аберрация

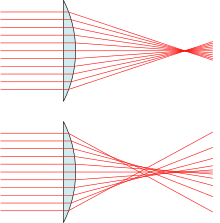
В оптике сферическая аберрация ( СА ) — это тип аберрации , встречающийся в оптических системах, имеющих элементы со сферическими поверхностями . Это явление обычно влияет на линзы и изогнутые зеркала , поскольку эти компоненты часто имеют сферическую форму для простоты изготовления. Световые лучи, которые падают на сферическую поверхность не по центру, преломляются или отражаются больше или меньше, чем те, которые падают близко к центру. Это отклонение снижает качество изображений, создаваемых оптическими системами. Эффект сферической аберрации был впервые выявлен в 11 веке Ибн аль-Хайсамом, который обсуждал его в своей работе Kitāb al-Manāẓir . ^[1]

Обзор

Сферическая линза имеет апланатическую точку (т. е. не имеет сферической аберрации) только на боковом расстоянии от оптической оси, равном радиусу сферической поверхности, деленному на показатель преломления материала линзы.

Сферическая аберрация делает фокус телескопов и других инструментов неидеальным. Это важный эффект, поскольку сферические формы гораздо проще производить, чем асферические. Во многих случаях для компенсации сферической аберрации дешевле использовать несколько сферических элементов, чем использовать одну асферическую линзу .

«Положительная» сферическая аберрация означает, что лучи вблизи внешнего края линзы изгибаются больше, чем можно было бы предсказать для идеальной линзы. «Отрицательная» сферическая аберрация означает, что такие лучи изгибаются меньше, чем можно было бы предсказать.

Эффект пропорционален четвертой степени диаметра и обратно пропорционален третьей степени фокусного расстояния, поэтому он гораздо более выражен при коротких фокусных отношениях , т. е. у «быстрых» объективов.

Продольные сечения сфокусированного пучка с отрицательной (верхний ряд), нулевой (средний ряд) и положительной сферической аберрацией (нижний ряд). Линза находится слева.

Исправление

В линзовых системах аберрации можно минимизировать, используя комбинации выпуклых и вогнутых линз или используя асферические линзы или апланатические линзы.

Системы линз с коррекцией аберраций обычно проектируются с помощью численной трассировки лучей . Для простых конструкций иногда можно аналитически рассчитать параметры, которые минимизируют сферическую аберрацию. Например, в конструкции, состоящей из одной линзы со сферическими поверхностями и заданным расстоянием до объекта o , расстоянием до изображения i и показателем преломления n , можно минимизировать сферическую аберрацию, регулируя радиусы кривизны и передней и задней поверхностей линзы таким образом, что ${\displaystyle R_{1}}$ ${\displaystyle R_{2}}$

${\displaystyle {\frac {R_{1}+R_{2}}{R_{1}-R_{2}}}={\frac {2\left(n^{2}-1\right)}{n+2}}\left({\frac {i+o}{i-o}}\right)}$, где знаки радиусов следуют декартову соглашению о знаках.

Точечный источник , изображенный системой с отрицательной (верхний ряд), нулевой (средний ряд) и положительной сферической аберрацией (нижний ряд). Средний столбец показывает сфокусированное изображение, столбцы слева показывают расфокусировку внутрь, а столбцы справа показывают расфокусировку наружу.

Для небольших телескопов, использующих сферические зеркала с фокусным расстоянием меньшеж /10, свет от удаленного точечного источника (например, звезды ) не фокусируется в одной точке. В частности, свет, падающий на внутреннюю часть зеркала, фокусируется дальше от зеркала, чем свет, падающий на внешнюю часть. В результате изображение не может быть сфокусировано так же резко, как если бы аберрации не было. Из-за сферической аберрации телескопы с фокусным отношением менееж /10обычно изготавливаются с использованием несферических зеркал или корректирующих линз.

Сферическую аберрацию можно устранить, сделав линзы с асферической поверхностью. Декарт показал, что линзы, поверхности которых представляют собой хорошо подобранные декартовы овалы (вращающиеся вокруг центральной оси симметрии), могут идеально отображать свет из точки на оси или из бесконечности в направлении оси. Такая конструкция обеспечивает полностью безаберрационную фокусировку света от удаленного источника. ^[2]

В 2018 году Рафаэль Г. Гонсалес-Акунья и Эктор А. Чапарро-Ромо, аспиранты Национального автономного университета Мексики и Монтеррейского института технологий и высшего образования в Мексике, нашли замкнутую формулу для поверхности линзы, которая устраняет сферическую аберрацию. ^{[3] [4] [5]} Их уравнение можно применить для указания формы одной поверхности линзы, где другая поверхность имеет любую заданную форму.

Оценка диаметра аберрированного пятна

Многие способы оценки диаметра сфокусированного пятна из-за сферической аберрации основаны на лучевой оптике. Однако лучевая оптика не считает, что свет — это электромагнитная волна. Поэтому результаты могут быть неверными из-за эффектов интерференции, возникающих из-за волновой природы света.

нотация Коддингтона

Довольно простой формализм, основанный на лучевой оптике, который справедлив только для тонких линз, — это обозначение Коддингтона. ^[6] В дальнейшем n — показатель преломления линзы, o — расстояние до объекта, i — расстояние до изображения, h — расстояние от оптической оси, на котором самый внешний луч входит в линзу, — первый радиус линзы, — второй радиус линзы, а f — фокусное расстояние линзы. Расстояние h можно понимать как половину чистой апертуры. ${\displaystyle R_{1}}$ ${\displaystyle R_{2}}$

Используя факторы Коддингтона для формы, s , и положения, p ,

${\displaystyle {\begin{aligned}s&={\frac {R_{2}+R_{1}}{R_{2}-R_{1}}}\\[8pt]p&={\frac {i-o}{i+o}},\end{aligned}}}$

можно записать продольную сферическую аберрацию как ^[6]

${\displaystyle \mathrm {LSA} ={\frac {1}{8n(n-1)}}\cdot {\frac {h^{2}i^{2}}{f^{3}}}\left({\frac {n+2}{n-1}}s^{2}+2(2n+2)sp+(3n+2)(n-1)^{2}p^{2}+{\frac {n^{3}}{n-1}}\right)}$

Если фокусное расстояние f намного больше продольной сферической аберрации LSA, то поперечная сферическая аберрация TSA, соответствующая диаметру фокусного пятна, определяется выражением

${\displaystyle \mathrm {TSA} ={\frac {h}{i}}\mathrm {LSA} }$

Смотрите также

• Ахроматическая линза
• Космический телескоп Хаббл
• телескоп Максутова
• Параболический отражатель
• Телескоп Ричи-Кретьена
• Пластина корректора Шмидта
• Мягкий фокус

Ссылки

1. Будриуа, Аззедин; Рашед, Рошди; Лакшминараянан, Васудеван (2017-08-15). Наука, основанная на свете: технологии и устойчивое развитие, наследие Ибн аль-Хайтама. CRC Press. ISBN 978-1-351-65112-7.
2. Вилларино, Марк Б. (2007). «Идеальная линза Декарта». arXiv : 0704.1059 [math.GM].
3. Мачука, Эдуардо (5 июля 2019 г.). «Прощай, аберрация: физик решает 2000-летнюю оптическую проблему». PetaPixel . Получено 10 июля 2019 г. .
4. Гонсалес-Акунья, Рафаэль Г.; Чапарро-Ромо, Эктор А. (2018). «Общая формула конструкции биасферических синглетных линз без сферических аберраций». Прикладная оптика . 57 (31): 9341–9345. arXiv : 1811.03792 . Бибкод : 2018ApOpt..57.9341G. дои : 10.1364/AO.57.009341. PMID  30461981. S2CID  53695913.
5. Лишевски, Эндрю (7 августа 2019 г.). «Мексиканский физик решил 2000-летнюю проблему, которая приведет к созданию более дешевых и острых линз». Gizmodo . Получено 7 августа 2019 г.
6. Smith, TT (1922). «Сферическая аберрация в тонких линзах». Научные труды Бюро стандартов . 18 : 559–584. doi : 10.6028/nbsscipaper.127 .

Внешние ссылки

• Сферическая аберрация. Архивировано 23 июля 2012 г. на Wayback Machine на сайте vanwalree.com , PA van Walree, просмотрено 28 января 2007 г.
• http://www.telescope-optics.net/Sphereal1.htm
• Статьи на других языках по уравнению Акунья-Ромо: испанский, немецкий, итальянский, русский