В материаловедении твёрдость (антоним: мягкость ) является мерой сопротивления локализованной пластической деформации , такой как вдавливание (по площади) или царапина (линейная), вызванной механически либо нажатием , либо истиранием . В целом, различные материалы различаются по своей твёрдости; например , твёрдые металлы, такие как титан и бериллий, твёрже мягких металлов, таких как натрий и металлическое олово , или дерева и обычных пластиков . Макроскопическая твёрдость, как правило, характеризуется прочными межмолекулярными связями , но поведение твёрдых материалов под действием силы является сложным; поэтому твёрдость можно измерить разными способами, такими как твёрдость при царапании , твёрдость при вдавливании и твёрдость по отскоку. Твёрдость зависит от пластичности , упругой жёсткости , пластичности , деформации , прочности , вязкоупругости , и вязкости . Распространенными примерами твёрдого вещества являются керамика , бетон , некоторые металлы и сверхтвёрдые материалы , которые можно противопоставить мягкому веществу .

Существует три основных типа измерений твердости: царапина, вдавливание и отскок. В каждом из этих классов измерений существуют отдельные шкалы измерений. По практическим причинам для преобразования одной шкалы в другую используются таблицы преобразования .
Твердость к царапинам — это мера того, насколько устойчив образец к трещинам или постоянной пластической деформации из-за трения острым предметом. [1] Принцип заключается в том, что предмет, изготовленный из более твердого материала, поцарапает предмет, изготовленный из более мягкого материала. При испытании покрытий твердость к царапинам относится к силе, необходимой для прорезания пленки до подложки. Наиболее распространенным испытанием является шкала Мооса , которая используется в минералогии . Одним из инструментов для проведения этого измерения является склерометр .
Другим инструментом, используемым для проведения этих испытаний, является карманный твердомер . Этот инструмент состоит из весовой штанги с градуированными отметками, прикрепленной к четырехколесной тележке. Царапающий инструмент с острым ободом устанавливается под определенным углом к испытательной поверхности. Для его использования к весовой штанге на одной из градуированных отметок добавляется груз известной массы, затем инструмент протягивается по испытательной поверхности. Использование груза и отметок позволяет применять известное давление без необходимости использования сложного оборудования. [2]
Твердость при вдавливании измеряет сопротивление образца деформации материала из-за постоянной нагрузки сжатия от острого предмета. Тесты на твердость при вдавливании в основном используются в машиностроении и металлургии . Тесты работают на основе базовой предпосылки измерения критических размеров отпечатка, оставленного специально рассчитанным и нагруженным индентором. Распространенными шкалами твердости при вдавливании являются Роквелл , Виккерс , Шор и Бринелль , среди прочих.
Твердость отскока , также известная как динамическая твердость , измеряет высоту «отскока» молотка с алмазным наконечником, упавшего с фиксированной высоты на материал. Этот тип твердости связан с эластичностью . Устройство, используемое для проведения этого измерения, известно как склероскоп . [3] Две шкалы, которые измеряют твердость отскока, — это тест твердости отскока Либа и шкала твердости Беннета. Метод ультразвукового контактного импеданса (UCI) определяет твердость путем измерения частоты колеблющегося стержня. Стержень состоит из металлического вала с вибрирующим элементом и алмаза в форме пирамиды, установленного на одном конце. [4]
Существует пять процессов упрочнения: упрочнение Холла-Петча , деформационное упрочнение , упрочнение твердого раствора , дисперсионное упрочнение и мартенситное превращение .

В механике твердого тела твердые тела обычно реагируют на силу тремя способами , в зависимости от величины силы и типа материала:
Прочность — это мера предела упругого диапазона материала или упругого и пластичного диапазонов вместе. Это количественно определяется как прочность на сжатие , прочность на сдвиг , прочность на растяжение в зависимости от направления задействованных сил. Предел прочности — это инженерная мера максимальной нагрузки, которую может выдержать часть определенного материала и геометрии.
Хрупкость в техническом смысле — это тенденция материала к разрушению с очень небольшой или необнаружимой пластической деформацией заранее. Таким образом, в технических терминах материал может быть как хрупким, так и прочным. В повседневном использовании «хрупкость» обычно относится к тенденции к разрушению под действием небольшой силы, что демонстрирует как хрупкость, так и недостаток прочности (в техническом смысле). Для совершенно хрупких материалов предел текучести и предел прочности одинаковы, поскольку они не испытывают обнаруживаемой пластической деформации. Противоположностью хрупкости является пластичность .
Прочность материала — это максимальное количество энергии, которое он может поглотить до разрушения, что отличается от количества силы , которое может быть приложено. Прочность , как правило, мала для хрупких материалов, поскольку упругие и пластические деформации позволяют материалам поглощать большие количества энергии.
Твердость увеличивается с уменьшением размера частиц . Это известно как соотношение Холла-Петча . Однако ниже критического размера зерна твердость уменьшается с уменьшением размера зерна. Это известно как обратный эффект Холла-Петча.
Твердость материала к деформации зависит от его микропрочности или модуля сдвига в малых масштабах в любом направлении, а не от каких-либо свойств жесткости или упругости, таких как модуль объемной упругости или модуль Юнга . Жесткость часто путают с твердостью. [5] [6] Некоторые материалы жестче алмаза (например, осмий), но не тверже и склонны к скалыванию и шелушению в виде чешуйчатых или игольчатых образований.

Ключом к пониманию механизма, лежащего в основе твердости, является понимание металлической микроструктуры , или структуры и расположения атомов на атомном уровне. Фактически, наиболее важные металлические свойства, критически важные для производства современных товаров, определяются микроструктурой материала. [7] На атомном уровне атомы в металле расположены в упорядоченном трехмерном массиве, называемом кристаллической решеткой . Однако в действительности данный образец металла, скорее всего, никогда не будет содержать последовательную монокристаллическую решетку. Данный образец металла будет содержать много зерен, причем каждое зерно будет иметь довольно последовательный рисунок массива. В еще меньшем масштабе каждое зерно содержит неровности.
Существует два типа неровностей на уровне зерен микроструктуры, которые отвечают за твердость материала. Эти неровности — точечные дефекты и линейные дефекты. Точечный дефект — это неровность, расположенная в одном узле решетки внутри общей трехмерной решетки зерна. Существует три основных точечных дефекта. Если в массиве отсутствует атом, образуется дефект вакансии . Если в узле решетки, который обычно должен быть занят атомом металла, находится другой тип атома, образуется дефект замещения. Если в узле, где его обычно не должно быть, находится атом, образуется межузельный дефект. Это возможно, поскольку между атомами в кристаллической решетке существует пространство. В то время как точечные дефекты — это неровности в одном узле кристаллической решетки, линейные дефекты — это неровности в плоскости атомов. Дислокации — это тип линейного дефекта, включающего несовпадение этих плоскостей. В случае краевой дислокации полуплоскость атомов заклинивается между двумя плоскостями атомов. В случае винтовой дислокации две плоскости атомов смещены, а между ними проходит винтовая решетка. [8]
В стеклах твердость, по-видимому, линейно зависит от числа топологических ограничений, действующих между атомами сети. [9] Таким образом, теория жесткости позволила предсказать значения твердости в зависимости от состава.
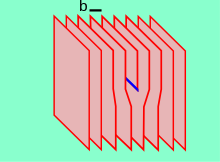
Дислокации обеспечивают механизм для скольжения плоскостей атомов и, таким образом, метод пластической или постоянной деформации. [7] Плоскости атомов могут переворачиваться с одной стороны дислокации на другую, эффективно позволяя дислокации проходить через материал и деформировать материал постоянно. Движение, допускаемое этими дислокациями, вызывает снижение твердости материала.
Способ подавления движения плоскостей атомов и, таким образом, упрочнения их, включает взаимодействие дислокаций друг с другом и междоузельными атомами. Когда дислокация пересекается со второй дислокацией, она больше не может проходить через кристаллическую решетку. Пересечение дислокаций создает опорную точку и не позволяет плоскостям атомов продолжать скользить друг по другу [10] Дислокация также может быть закреплена взаимодействием с междоузельными атомами. Если дислокация вступает в контакт с двумя или более междоузельными атомами, скольжение плоскостей снова будет нарушено. Междоузельные атомы создают опорные точки или точки закрепления таким же образом, как и пересекающиеся дислокации.
Изменяя наличие междоузельных атомов и плотность дислокаций, можно контролировать твердость конкретного металла. Хотя это и кажется нелогичным, но по мере увеличения плотности дислокаций создается больше пересечений и, следовательно, больше точек закрепления. Аналогично, по мере добавления большего количества междоузельных атомов образуется больше точек закрепления, которые препятствуют движению дислокаций. В результате, чем больше точек закрепления добавляется, тем тверже становится материал.
Следует обратить особое внимание на взаимосвязь между числом твердости и кривой напряжение-деформация, демонстрируемой материалом. Последняя, которая обычно получается с помощью испытания на растяжение , фиксирует полную реакцию пластичности материала (который в большинстве случаев является металлом). Фактически это зависимость (истинной) пластической деформации по фон Мизесу от (истинного) напряжения по фон Мизесу , но это легко получить из кривой номинальное напряжение – номинальная деформация (в режиме предварительного сужения ), которая является непосредственным результатом испытания на растяжение. Это соотношение можно использовать для описания того, как материал будет реагировать практически на любую ситуацию нагрузки, часто с использованием метода конечных элементов (FEM). Это применимо к результату испытания на вдавливание (с заданным размером и формой индентора и заданной приложенной нагрузкой).
Однако, хотя число твердости, таким образом, зависит от соотношения напряжение-деформация, вывести последнее из первого далеко не просто и не пытаются каким-либо строгим образом во время обычного испытания на твердость. (На самом деле, метод пластометрии индентирования , который включает итеративное моделирование FEM испытания на вдавливание, позволяет получить кривую напряжение-деформация с помощью индентирования, но это выходит за рамки обычного испытания на твердость.) Число твердости является всего лишь полуколичественным показателем сопротивления пластической деформации. Хотя твердость определяется аналогичным образом для большинства типов испытаний — обычно как нагрузка, деленная на площадь контакта — числа, полученные для конкретного материала, различны для разных типов испытаний и даже для одного и того же испытания с разными приложенными нагрузками. Иногда предпринимаются попытки [11] [12] [13] [14] [15] определить простые аналитические выражения, которые позволяют получить характеристики кривой напряжения-деформации, в частности предел текучести и предел прочности на разрыв (UTS), из определенного типа числа твердости. Однако все они основаны на эмпирических корреляциях, часто специфичных для определенных типов сплавов: даже при таком ограничении полученные значения часто весьма ненадежны. Основная проблема заключается в том, что металлы с различными сочетаниями предела текучести и характеристик упрочнения могут демонстрировать одно и то же число твердости. К использованию чисел твердости для любых количественных целей следует, в лучшем случае, подходить со значительной осторожностью.