Термоэлектрический эффект

Прямое преобразование разницы температур в электрическое напряжение и наоборот

Термоэлектрический эффект — это прямое преобразование разницы температур в электрическое напряжение и наоборот с помощью термопары . ^[1] Термоэлектрическое устройство создает напряжение, когда на каждой стороне разная температура. И наоборот, когда к нему приложено напряжение, тепло передается с одной стороны на другую, создавая разницу температур.

Этот эффект может быть использован для генерации электроэнергии , измерения температуры или изменения температуры объектов. Поскольку направление нагрева и охлаждения зависит от приложенного напряжения, термоэлектрические устройства могут использоваться в качестве регуляторов температуры.

Термин «термоэлектрический эффект» охватывает три отдельно идентифицированных эффекта: эффект Зеебека (разница температур вызывает электродвижущие силы), эффект Пельтье (термопары создают разницу температур) и эффект Томсона (коэффициент Зеебека изменяется в зависимости от температуры). Эффекты Зеебека и Пельтье являются различными проявлениями одного и того же физического процесса; учебники могут называть этот процесс эффектом Пельтье–Зеебека (разделение происходит от независимых открытий французского физика Жана Шарля Атаназа Пельтье и балтийского немецкого физика Томаса Иоганна Зеебека ). Эффект Томсона является расширением модели Пельтье–Зеебека и приписывается лорду Кельвину .

Джоулевое тепло , тепло, которое генерируется при прохождении тока через проводящий материал, обычно не называется термоэлектрическим эффектом. Эффекты Пельтье-Зеебека и Томсона являются термодинамически обратимыми , ^[2] тогда как джоулево тепло — нет.

Источник

В атомном масштабе температурный градиент заставляет носители заряда в материале диффундировать с горячей стороны на холодную. Это происходит из-за того, что частицы носителей заряда имеют более высокие средние скорости (и, следовательно, кинетическую энергию ) при более высоких температурах, что приводит к их миграции в среднем к более холодной стороне, в процессе переноса тепла через материал. ^[3]

В зависимости от свойств материала и природы носителей заряда (будь то положительные дырки в объемном материале или электроны с отрицательным зарядом), тепло может переноситься в любом направлении относительно напряжения. Полупроводники n-типа и p -типа часто объединяются последовательно, поскольку они имеют противоположные направления переноса тепла, что определяется знаком их коэффициентов Зеебека . ^[4]

эффект Зеебека

Эффект Зеебека в термобатарее, изготовленной из железной и медной проволоки

Термоэлектрическая цепь, состоящая из материалов с различными коэффициентами Зеебека (p- легированные и n-легированные полупроводники), сконфигурированная как термоэлектрический генератор . Если нагрузочный резистор внизу заменить вольтметром , цепь будет функционировать как термопара, чувствительная к температуре .

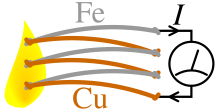
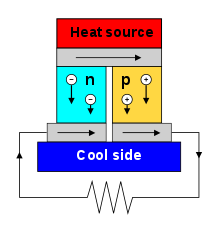
Эффект Зеебека — это электродвижущая сила (ЭДС) , которая возникает между двумя точками электропроводящего материала, когда между ними существует разница температур. ЭДС называется ЭДС Зеебека (или термо/термо/термоэлектрической ЭДС). Соотношение между ЭДС и разницей температур называется коэффициентом Зеебека. Термопара измеряет разность потенциалов между горячим и холодным концом двух разнородных материалов. Эта разность потенциалов пропорциональна разнице температур между горячим и холодным концами. Впервые обнаруженный в 1794 году итальянским ученым Алессандро Вольта , ^{[5] [примечание 1]} он назван в честь русского физика балтийского немца Томаса Иоганна Зеебека , который заново открыл его в 1821 году.

Зеебек наблюдал то, что он назвал «термомагнитным эффектом», при котором магнитная стрелка компаса отклонялась замкнутой петлей, образованной двумя различными металлами, соединенными в двух местах, с приложенной разницей температур между соединениями. Датский физик Ганс Христиан Эрстед заметил, что разница температур фактически приводила в движение электрический ток, а генерация магнитного поля была косвенным следствием, и поэтому ввел более точный термин «термоэлектричество». ^[6]

Эффект Зеебека является классическим примером электродвижущей силы (ЭДС) и приводит к измеряемым токам или напряжениям таким же образом, как и любая другая ЭДС. Локальная плотность тока определяется как

$${\displaystyle \mathbf {J} =\sigma (-\nabla V+\mathbf {E} _{\text{emf}}),}$$

где - локальное напряжение , ^[7] и - локальная проводимость . В общем случае эффект Зеебека локально описывается созданием электродвижущего поля ${\displaystyle V}$ ${\displaystyle \sigma }$

$${\displaystyle \mathbf {E} _{\text{emf}}=-S\nabla T,}$$

где — коэффициент Зеебека (также известный как термоЭДС), свойство локального материала, а — градиент температуры. ${\displaystyle S}$ ${\displaystyle \nabla T}$

Коэффициенты Зеебека обычно изменяются в зависимости от температуры и сильно зависят от состава проводника. Для обычных материалов при комнатной температуре коэффициент Зеебека может варьироваться в диапазоне значений от −100 мкВ/К до +1000 мкВ/К (см. статью Коэффициент Зеебека для получения дополнительной информации).

Приложения

На практике термоэлектрические эффекты по существу ненаблюдаемы для локализованной горячей или холодной точки в одном однородном проводящем материале, поскольку общие ЭДС от возрастающих и убывающих градиентов температуры будут полностью компенсироваться. Присоединение электрода к горячей точке в попытке измерить локально смещенное напряжение будет успешным лишь отчасти: это означает, что внутри электрода появится другой температурный градиент, и поэтому общая ЭДС будет зависеть от разницы коэффициентов Зеебека между электродом и проводником, к которому он прикреплен.

Термопары включают в себя два провода, каждый из разного материала, которые электрически соединены в области неизвестной температуры. Свободные концы измеряются в состоянии разомкнутой цепи (без какого-либо тока, ). Хотя коэффициенты Зеебека материалов нелинейно зависят от температуры и различны для двух материалов, состояние разомкнутой цепи означает, что везде. Поэтому (см. статью о термопарах для получения более подробной информации) напряжение, измеренное на свободных концах проводов, напрямую зависит от неизвестной температуры и при этом полностью независимо от других деталей, таких как точная геометрия проводов. Эта прямая связь позволяет использовать схему термопары в качестве простого некалиброванного термометра, при условии знания разницы в кривых -vs- двух материалов и эталонной температуры на измеренных свободных концах проводов. ${\displaystyle \mathbf {J} =0}$ ${\displaystyle S}$ ${\displaystyle \nabla V=-S\nabla T}$ ${\displaystyle S}$ ${\displaystyle T}$

Термоэлектрическая сортировка работает аналогично термопаре, но использует неизвестный материал вместо неизвестной температуры: металлический зонд известного состава поддерживается при постоянной известной температуре и контактирует с неизвестным образцом, который локально нагревается до температуры зонда, тем самым обеспечивая приблизительное измерение неизвестного коэффициента Зеебека . Это может помочь различать разные металлы и сплавы. ${\displaystyle S}$

Термобатареи формируются из множества термопар, соединенных последовательно, зигзагообразно перемещаясь между горячим и холодным. Это умножает выходное напряжение.

Термоэлектрические генераторы похожи на термопару/термобатарею, но вместо этого потребляют ток из генерируемого напряжения, чтобы извлекать мощность из разницы температур. Они оптимизированы иначе, чем термопары, используя высококачественные термоэлектрические материалы в термобатарее, чтобы максимизировать извлеченную мощность. Хотя эти генераторы не особенно эффективны, у них есть преимущество в том, что они не имеют движущихся частей.

Эффективность

эффект Пельтье

Схема Зеебека, сконфигурированная как термоэлектрический охладитель

Видео с тепловизионной камеры элемента Пельтье

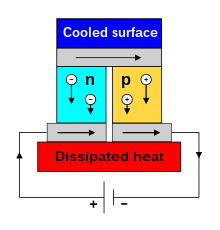
Когда электрический ток проходит через цепь термопары , тепло генерируется на одном соединении и поглощается на другом соединении. Это известно как эффект Пельтье : наличие нагрева или охлаждения на электрифицированном соединении двух разных проводников. Эффект назван в честь французского физика Жана Шарля Атаназа Пельтье , который открыл его в 1834 году. ^[8] Когда ток течет через соединение между двумя проводниками, A и B, тепло может генерироваться или отводиться в соединении. Тепло Пельтье, генерируемое в соединении за единицу времени, равно

$${\displaystyle {\dot {Q}}=(\Pi _{\text{A}}-\Pi _{\text{B}})I,}$$

где и — коэффициенты Пельтье проводников A и B, а — электрический ток (от A до B). Общее количество выделяемого тепла определяется не только эффектом Пельтье, на него также могут влиять джоулев нагрев и эффекты температурного градиента (см. ниже). ${\displaystyle \Pi _{\text{A}}}$ ${\displaystyle \Pi _{\text{B}}}$ ${\displaystyle I}$

Коэффициенты Пельтье показывают, сколько тепла переносится на единицу заряда. Поскольку ток заряда должен быть непрерывным через соединение, связанный с ним поток тепла будет создавать разрыв, если и различны. Эффект Пельтье можно рассматривать как обратный аналог эффекта Зеебека (аналогично обратной ЭДС в магнитной индукции): если простая термоэлектрическая цепь замкнута, то эффект Зеебека будет вызывать ток, который, в свою очередь (благодаря эффекту Пельтье), всегда будет переносить тепло от горячего к холодному соединению. Тесная связь между эффектами Пельтье и Зеебека может быть замечена в прямой связи между их коэффициентами: (см. ниже). ${\displaystyle \Pi _{\text{A}}}$ ${\displaystyle \Pi _{\text{B}}}$ ${\displaystyle \Pi =TS}$

Типичный тепловой насос Пельтье включает в себя несколько последовательных соединений, через которые проходит ток. Некоторые соединения теряют тепло из-за эффекта Пельтье, в то время как другие получают тепло. Термоэлектрические тепловые насосы используют это явление, как и термоэлектрические охлаждающие устройства, используемые в холодильниках.

Приложения

Эффект Пельтье может быть использован для создания теплового насоса . Примечательно, что термоэлектрический охладитель Пельтье представляет собой компактный холодильник, не имеющий циркулирующей жидкости или движущихся частей. Такие холодильники полезны в приложениях, где их преимущества перевешивают недостаток их очень низкой эффективности.

Тепловые насосы Пельтье могут использоваться и в других тепловых насосах, например, в осушителях воздуха .

Термоэлектрические охладители тривиально обратимы, поскольку их можно использовать в качестве нагревателей, просто изменяя полярность тока. В отличие от обычного резистивного электрического нагрева ( нагрева Джоуля ), который изменяется пропорционально квадрату тока, эффект термоэлектрического нагрева линейный по току (по крайней мере, для малых токов), но требует холодного стока для пополнения тепловой энергии. Этот быстрый обратный эффект нагрева и охлаждения используется многими современными термоциклерами , лабораторными устройствами, используемыми для амплификации ДНК с помощью полимеразной цепной реакции (ПЦР). ПЦР требует циклического нагрева и охлаждения образцов до определенных температур. Включение множества термопар в небольшое пространство позволяет амплифицировать много образцов параллельно.

эффект Томсона

Для некоторых материалов коэффициент Зеебека не является постоянным по температуре, и поэтому пространственный градиент температуры может привести к градиенту коэффициента Зеебека. Если ток проходит через этот градиент, то возникнет непрерывная версия эффекта Пельтье. Этот эффект Томсона был предсказан и позже обнаружен в 1851 году лордом Кельвином (Уильямом Томсоном). ^[9] Он описывает нагревание или охлаждение проводника с током с градиентом температуры. Если плотность тока проходит через однородный проводник, эффект Томсона предсказывает скорость производства тепла на единицу объема. ${\displaystyle \mathbf {J} }$

$${\displaystyle {\dot {q}}=-{\mathcal {K}}\mathbf {J} \cdot \nabla T,}$$

где — градиент температуры, а — коэффициент Томсона. Эффект Томсона — это проявление направления потока электрических носителей относительно градиента температуры внутри проводника. Они поглощают энергию (тепло), текущую в направлении, противоположном тепловому градиенту, увеличивая свою потенциальную энергию, и, когда текут в том же направлении, что и тепловой градиент, они выделяют тепло, уменьшая свою потенциальную энергию. ^[10] Коэффициент Томсона связан с коэффициентом Зеебека как (см. ниже). Это уравнение, однако, пренебрегает джоулевым нагревом и обычной теплопроводностью (см. полные уравнения ниже). ${\displaystyle \nabla T}$ ${\displaystyle {\mathcal {K}}}$ ${\displaystyle {\mathcal {K}}=T{\tfrac {dS}{dT}}}$

Полные термоэлектрические уравнения

Часто в работе реального термоэлектрического устройства задействовано более одного из вышеперечисленных эффектов. Эффект Зеебека, эффект Пельтье и эффект Томсона можно объединить в последовательный и строгий способ, описанный здесь; это также включает эффекты джоулева нагрева и обычной теплопроводности. Как указано выше, эффект Зеебека генерирует электродвижущую силу, что приводит к уравнению тока ^[11]

$${\displaystyle \mathbf {J} =\sigma (-{\boldsymbol {\nabla }}V-S\nabla T).}$$

Для описания эффектов Пельтье и Томсона мы должны рассмотреть поток энергии. Если температура и заряд изменяются со временем, полное термоэлектрическое уравнение для накопления энергии, , имеет вид ^[11] ${\displaystyle {\dot {e}}}$

$${\displaystyle {\dot {e}}=\nabla \cdot (\kappa \nabla T)-\nabla \cdot (V+\Pi )\mathbf {J} +{\dot {q}}_{\text{ext}},}$$

где - теплопроводность . Первый член - закон теплопроводности Фурье , а второй член показывает энергию, переносимую токами. Третий член, - это тепло, добавленное от внешнего источника (если применимо). ${\displaystyle \kappa }$ ${\displaystyle {\dot {q}}_{\text{ext}}}$

Если материал достиг устойчивого состояния, то распределение заряда и температуры стабильно, поэтому и . Используя эти факты и второе соотношение Томсона (см. ниже), уравнение теплопроводности можно упростить до ${\displaystyle {\dot {e}}=0}$ ${\displaystyle \nabla \cdot \mathbf {J} =0}$

$${\displaystyle -{\dot {q}}_{\text{ext}}=\nabla \cdot (\kappa \nabla T)+\mathbf {J} \cdot \left(\sigma ^{-1}\mathbf {J} \right)-T\mathbf {J} \cdot \nabla S.}$$

Средний член — это джоулев нагрев, а последний член включает в себя как эффекты Пельтье ( на стыке), так и Томсона ( в тепловом градиенте). В сочетании с уравнением Зеебека для это можно использовать для решения стационарных профилей напряжения и температуры в сложной системе. ${\displaystyle \nabla S}$ ${\displaystyle \nabla S}$ ${\displaystyle \mathbf {J} }$

Если материал не находится в устойчивом состоянии, полное описание должно включать динамические эффекты, такие как связанные с электрической емкостью , индуктивностью и теплоемкостью .

Термоэлектрические эффекты лежат за пределами равновесной термодинамики. Они обязательно включают в себя непрерывные потоки энергии. По крайней мере, они включают в себя три тела или термодинамические подсистемы, организованные определенным образом, вместе с особым расположением окружения. Три тела — это два разных металла и область их соединения. Область соединения — это неоднородное тело, предположительно стабильное, не подвергающееся слиянию путем диффузии вещества. Окружение организовано так, чтобы поддерживать два температурных резервуара и два электрических резервуара.

Для воображаемого, но не возможного на самом деле термодинамического равновесия перенос тепла из горячего резервуара в холодный должен быть предотвращен с помощью специально согласованной разницы напряжений, поддерживаемой электрическими резервуарами, а электрический ток должен быть равен нулю. Для устойчивого состояния должна быть по крайней мере некоторая передача тепла или некоторый ненулевой электрический ток. Два способа передачи энергии, как тепло и электрический ток, можно различить, когда есть три отдельных тела и различное расположение окружения.

Но в случае непрерывного изменения среды теплопередача и термодинамическая работа не могут быть однозначно разделены. Это сложнее, чем часто рассматриваемые термодинамические процессы, в которых связаны всего две соответственно однородные подсистемы.

отношения Томсона

В 1854 году лорд Кельвин обнаружил взаимосвязи между тремя коэффициентами, подразумевая, что эффекты Томсона, Пельтье и Зеебека являются различными проявлениями одного эффекта (уникально характеризуемого коэффициентом Зеебека). ^[12]

Первое соотношение Томсона ^[11]

$${\displaystyle {\mathcal {K}}\equiv {\frac {d\Pi }{dT}}-S,}$$

где — абсолютная температура, — коэффициент Томсона, — коэффициент Пельтье, — коэффициент Зеебека. Эту связь легко показать, учитывая, что эффект Томсона является непрерывной версией эффекта Пельтье. ${\displaystyle T}$ ${\displaystyle {\mathcal {K}}}$ ${\displaystyle \Pi }$ ${\displaystyle S}$

Второе соотношение Томсона:

$${\displaystyle \Pi =TS.}$$

Это соотношение выражает тонкую и фундаментальную связь между эффектами Пельтье и Зеебека. Оно не было удовлетворительно доказано до появления соотношений Онзагера , и стоит отметить, что это второе соотношение Томсона гарантируется только для симметричного относительно обращения времени материала; если материал помещен в магнитное поле или сам по себе является магнитно-упорядоченным ( ферромагнитным , антиферромагнитным и т. д.), то второе соотношение Томсона не принимает простую форму, показанную здесь. ^[13]

Теперь, используя второе соотношение, первое соотношение Томсона становится

$${\displaystyle {\mathcal {K}}=T{\tfrac {dS}{dT}}}$$

Коэффициент Томсона является уникальным среди трех основных термоэлектрических коэффициентов, поскольку он единственный, который можно измерить напрямую для отдельных материалов. Коэффициенты Пельтье и Зеебека можно легко определить только для пар материалов; следовательно, трудно найти значения абсолютных коэффициентов Зеебека или Пельтье для отдельного материала.

Если коэффициент Томсона материала измеряется в широком диапазоне температур, его можно интегрировать с помощью соотношений Томсона, чтобы определить абсолютные значения коэффициентов Пельтье и Зеебека. Это необходимо сделать только для одного материала, поскольку другие значения можно определить, измеряя попарно коэффициенты Зеебека в термопарах, содержащих эталонный материал, а затем добавляя абсолютный коэффициент Зеебека эталонного материала. Более подробную информацию об определении абсолютного коэффициента Зеебека см. в разделе Коэффициент Зеебека .

Смотрите также

• Барокалорический материал
• Эффект Нернста – термоэлектрическое явление, при котором образец, допускающий электропроводность в магнитном поле и градиенте температуры, перпендикулярны друг другу.
• Эффект Эттингсгаузена – термоэлектрическое явление, влияющее на ток в проводнике в магнитном поле.
• Пироэлектричество – создание электрической поляризации в кристалле после нагревания/охлаждения, эффект, отличный от термоэлектричества.
• Термоэлектронная эмиссия – освобождение заряженных частиц из горячего электрода.
• Термогальванический элемент – производство электроэнергии с помощью гальванического элемента с электродами, находящимися при разных температурах.
• Термобатарея
• Термофотоэлектричество – производство электроэнергии из тепловой энергии с использованием фотоэлектрического эффекта.

Ссылки

1. «Эффект Пельтье и термоэлектрическое охлаждение». ffden-2.phys.uaf.edu .
2. По мере того, как «показатель качества» стремится к бесконечности, эффект Пельтье–Зеебека может приводить в действие тепловой двигатель или холодильник с эффективностью, все более приближающейся к КПД Карно . Disalvo, FJ (1999). «Термоэлектрическое охлаждение и генерация электроэнергии». Science . 285 (5428): 703–706. doi :10.1126/science.285.5428.703. PMID  10426986.Любое устройство, работающее с КПД Карно, является термодинамически обратимым, что является следствием классической термодинамики .
3. "ТЕРМОЭЛЕКТРИЧЕСКИЕ ЯВЛЕНИЯ" (PDF) . Получено 2024-08-13 .
4. Prunet, G.; Pawula, F.; Fleury, G.; Cloutet, E.; Robinson, AJ; Hadziioannou, G.; Pakdel, A. (2021). «Обзор проводящих полимеров и их гибридов для гибких и носимых термоэлектрических приложений». Materials Today Physics . 18 : 100402. doi : 10.1016/j.mtphys.2021.100402. hdl : 2262/98609 .
5. Гупиль, Кристоф; Уэрдан, Хенни; Заброцкий, Кнуд; Зайферт, Вольфганг; Хинше, Ники Ф.; Мюллер, Экхард (2016). «Термодинамика и термоэлектричество». В Гупиле, Кристоф (ред.). Теория континуума и моделирование термоэлектрических элементов . Нью-Йорк: Wiley-VCH. стр. 2–3. ISBN 9783527413379.
6. См.:
   • Эрстед (1823 г.). «Nouvelles expériences de M. Seebeck sur les action électro-magnetiques» [Новые эксперименты г-на Зеебека по электромагнитным действиям]. Анналы де Химье . 2-я серия (на французском языке). 22 : 199–201.Со стр. 199–200: « Il faudra sans doute désormais различает новые классы электрических цепей по одному наименованию , что означает ; впредь выделять этот новый класс электрических цепей ориентировочным названием и в качестве такового я предлагаю выражение «термоэлектрические цепи» или, возможно, «термоэлектрические цепи»…)
   • Эрстед (1823 г.). «Notiz von neuen electricsch-magnetischen Versuchen des Herrn Seebeck in Berlin» [Уведомление о новых электромагнитных экспериментах г-на Зеебека в Берлине]. Аннален дер Физик (на немецком языке). 73 (4): 430–432. Бибкод : 1823АнП....73..430О. дои : 10.1002/andp.18230730410.
7. Напряжение в данном случае относится не к электрическому потенциалу, а к напряжению «вольтметра» , где — уровень Ферми . ${\displaystyle V=-\mu /e}$ ${\displaystyle \mu }$
8. Пельтье (1834). «Новые эксперименты по тепловому воздействию электрических токов». Annales de Chimie et de Physique (на французском языке). 56 : 371–386.
9. Томсон, Уильям (1857). "4. О механической теории термоэлектрических токов" . Труды Королевского общества Эдинбурга . 3 . Cambridge Univ. Press: 91–98. doi :10.1017/S0370164600027310 . Получено 7 февраля 2022 г. .
10. Роу, Дэвид Майкл (1994). CRC Handbook of Thermoelectrics . Boca Raton New York London [и т.д.]: CRC press. ISBN 0849301467.
11. Леон ван Доммелен (1 февраля 2002 г.). «А.11 Термоэлектрические эффекты». eng.famu.fsu.edu . Проверено 23 ноября 2022 г.
12. Томсон, Уильям (1857). «О динамической теории тепла. Часть V. Термоэлектрические токи». Труды Королевского общества Эдинбурга . 21 : 123–171. doi :10.1017/S0080456800032014. S2CID  120018011.
13. Существует обобщенное второе соотношение Томсона, связывающее анизотропные коэффициенты Пельтье и Зеебека с обратным магнитным полем и магнитным порядком. См., например, Rowe, DM, ed. (2010). Thermoelectrics Handbook: Macro to Nano . CRC Press . ISBN 9781420038903.

Примечания

1. В 1794 году Вольта обнаружил, что если между концами железного стержня существует разница температур, то это может вызвать спазмы лапки лягушки. Его аппарат состоял из двух стаканов с водой. В каждый стакан была погружена проволока, которая была соединена с одной или другой задней лапкой лягушки. Железный стержень был согнут в лук, и один конец нагревался в кипящей воде. Когда концы железного лука были погружены в два стакана, термоэлектрический ток проходил через лапки лягушки и заставлял их подергиваться. См.:
   • Вольта, Алессандро (1794). «Nuova memoria sull'elettricità Animale del Sig. Don Alessandro Volta… in alcune Lettere al Sig. Ab. Anton Maria Vassalli…» [Новые мемуары о животном электричестве дона Алессандро Вольты… в некоторых письмах к аббату Антонио Марии Вассалли…]. Annali di Chimica e Storia Naturale (Анналы химии и естественной истории) (на итальянском языке). 5 : 132–144.; см. стр. 139.
   • Перепечатано в: Вольта, Алессандро (1816) Collezione dell'Opere del Cavaliere Conte Alessandro Volta … [Сборник сочинений графа Алессандро Вольта…]. (на итальянском языке) Флоренция (Флоренция), (Италия): Гульельмо Пьятти. том. 2, часть 1. «Nuova memoria sull'elettricità Animale, divisa in tre Lettere, dirette al Signor Abate Anton Maria Vassalli… Lettera Prima» (Новые мемуары о животном электричестве, разделенные на три письма, адресованные аббату Антонио Марии Вассалли… Первое письмо ), стр. 197–206; см. стр. 202.
   Из (Вольта, 1794), с. 139: «… tuffava nell'acqua bollente un capo di tal arco per qualche mezzo minuto, … inetto de tutto ad eccitare le convulsioni dell'animale». (… Я окунул один конец такой дуги [железного стержня] в кипящую воду примерно на полминуты, затем вынул ее и, не давая ей времени остыть, возобновил эксперимент с двумя стаканами прохладной воды; и [ именно в этот момент лягушка в ванне билась в конвульсиях; и это [случалось] даже два, три, четыре раза, [при] повторении эксперимента; пока, [не] охладившись – такими погружениями, [которые были] более или (Менее продолжительное и многократное, или более длительное воздействие на воздух конца железного [стержня], который был] ранее погружен в горячую воду, эта дуга возвращалась [к состоянию] полной неспособности возбуждать судороги у животного.)

Дальнейшее чтение

• Rowe, DM, ред. (2006). Справочник по термоэлектричеству: от макро до нано . Taylor & Francis . doi :10.1201/9781420038903. ISBN 0-8493-2264-2. OCLC  70217582.
• Джек, П. М. (2003). «Физическое пространство как кватернионная структура I: уравнения Максвелла. Краткое примечание». arXiv : math-ph/0307038 .
• Безансон, Роберт М. (1985). Безансон, Роберт М. (ред.). Энциклопедия физики (3-е изд.). Ван Ностранд Рейнхольд. doi :10.1007/978-1-4615-6902-2. ISBN 0-442-25778-3.
• Иоффе, А.Ф. (1957). Полупроводниковые термоэлементы и термоэлектрическое охлаждение . Infosearch. ISBN 0-85086-039-3. OCLC  600476276.
• Томсон, Уильям (1851). «О механической теории термоэлектрических токов». Труды Королевского общества Эдинбурга . 3 (опубликовано в 1857 г.): 91–98. doi :10.1017/S0370164600027310.

Внешние ссылки

• Международное термоэлектрическое общество
• Фёлль, Хельмут (октябрь 2019 г.). "2.3.3 Термоэлектрические эффекты: общее рассмотрение". Электронные материалы . Кильский университет.
• Новостная статья о повышении эффективности термодиодов