stringtranslate.com

Тетрахорд

В теории музыки тетрахорд ( греч . τετράχορδoν ; лат . tetrachordum ) — это ряд из четырёх нот, разделённых тремя интервалами . В традиционной теории музыки тетрахорд всегда охватывал интервал чистой кварты , частотную пропорцию 4:3 (приблизительно 498 центов ) , но в современном использовании он означает любой четырёхнотный сегмент гаммы или тонового ряда , не обязательно связанный с конкретной системой настройки.

История

Название происходит от тетра (греч. tetra — «четыре чего-либо») и аккорд (греч. chordon — «струна» или «нота»). В древнегреческой музыкальной теории тетрахорд обозначал сегмент большей и меньшей совершенной системы, ограниченный неподвижными нотами ( греч . ἑστῶτες ); ноты между ними были подвижными ( греч . κινούμενοι ). Это буквально означает четыре струны , первоначально по отношению к инструментам, похожим на арфу, таким как лира или кифара, с неявным пониманием того, что четыре струны производили смежные (т. е. соединенные) ноты.

Современная теория музыки использует октаву как базовую единицу для определения настройки, тогда как древние греки использовали тетрахорд. Древнегреческие теоретики признавали, что октава является фундаментальным интервалом, но рассматривали ее как построенную из двух тетрахордов и целого тона . [1]

Древнегреческая теория музыки

Древнегреческая музыкальная теория различает три рода (ед. число: род ) тетрахордов. Эти роды характеризуются наибольшим из трех интервалов тетрахорда:

диатонический
Диатонический тетрахорд имеет характерный интервал, который меньше или равен половине общего интервала тетрахорда (или приблизительно 249  центов ). Этот характерный интервал обычно немного меньше (приблизительно 200 центов), становясь целым тоном . Классически диатонический тетрахорд состоит из двух интервалов в тон и одного в полутон , например, A–G–F–E.
Хроматический
Хроматический тетрахорд имеет характерный интервал, который больше, чем примерно половина общего интервала тетрахорда, но не так велик, как четыре пятых интервала (между примерно 249 и 398 центами). Классически характерный интервал — малая терция (примерно 300 центов), а два меньших интервала — равные полутона, например, A–G ♭ –F–E.
Энгармонический
Два греческих тетрахорда в энгармоническом роде, образующие энгармоническую дорийскую гамму
Энгармонический тетрахорд имеет характерный интервал, который больше, чем примерно четыре пятых от общего интервала тетрахорда. Классически характерный интервал — это дитон или большая терция , [2] а два меньших интервала — это четверти тона , например, A–Gдвойная квартира–Фнаполовину плоский–Э.

Когда составной интервал двух меньших интервалов меньше оставшегося ( несоставного ) интервала, группа из трех нот называется пикноном ( от pyknós , что означает «сжатый»). Это касается хроматических и энгармонических тетрахордов, но не диатонического (что означает «растянутый») тетрахорда.

Какова бы ни была настройка тетрахорда, его четыре ступени называются в порядке возрастания: hypate , parhypate , lichanos (или hypermese ), и mese , а для второго тетрахорда в построении системы — paramese , trite , paranete и nete . Hypate и mese , paramese и nete фиксированы и отстоят друг от друга на чистую кварту, в то время как положение parhypate и lichanos , или trite и paranete , подвижно.

Поскольку три рода просто представляют собой диапазоны возможных интервалов в пределах тетрахорда, были определены различные оттенки ( chroai ) с определенными настройками. После того, как род и оттенок тетрахорда определены, их расположение может производить три основных типа гамм, в зависимости от того, какая нота тетрахорда берется в качестве первой ноты гаммы. Сами тетрахорды остаются независимыми от гамм, которые они производят, и никогда не были названы в честь этих гамм греческими теоретиками. [3]

дорийский лад
Первая нота тетрахорда является также первой нотой гаммы.
Диатоника: Ми–Ре–До–Си | Ля–Соль–Фа–Ми
Хроматические: Ми–Ре ♭ –До–Си | Ля–Соль ♭ –Фа–Ми
Энгармонический: E–Dдвойная квартира–Снаполовину плоский–Б │ А–Гдвойная квартира–Фнаполовину плоский–Э
Фригийская гамма
Вторая нота тетрахорда (в нисходящем порядке) является первой нотой гаммы.
Диатоника: D–C–B | A–G–F–E | D
Хроматика: D ♭ –C–B | A–G ♭ –F–E | D ♭
Энгармонический: Dдвойная квартира–Снаполовину плоский–Б | А–Гдвойная квартира–Фнаполовину плоский–Э | Ддвойная квартира
Лидийский лад
Третья нота тетрахорда (в нисходящем порядке) является первой нотой гаммы.
Диатоника: C–B | A–G–F–E | D–C
Хроматические: C–B | A–G ♭ –F–E | D ♭ –C
Энгармонический: Cнаполовину плоский–Б | А–Гдвойная квартира–Фнаполовину плоский–Э | Ддвойная квартира–Снаполовину плоский

Во всех случаях крайние ноты тетрахордов, E–B и A–E, остаются фиксированными, тогда как ноты между ними различаются в зависимости от рода.

Пифагорейские настройки

Вот традиционные пифагорейские настройки диатонических и хроматических тетрахордов:

Вот типичная пифагорейская настройка энгармонического рода, приписываемая Архиту :

Число струн на классической лире варьировалось в разные эпохи и, возможно, в разных местностях — четыре, семь и десять были любимыми числами. Более крупные гаммы строятся из конъюнктных или дизъюнктных тетрахордов. Конъюнктные тетрахорды разделяют ноту, в то время как дизъюнктные тетрахорды разделены дизъюнктным тоном 9/8 (пифагорейская большая секунда). Чередующиеся конъюнктные и дизъюнктные тетрахорды образуют гамму, которая повторяется в октавах (как в знакомой диатонической гамме , созданной таким образом из диатонического рода), но это была не единственная аранжировка.

Греки анализировали роды, используя различные термины, включая диатонический, энгармонический и хроматический. Гаммы строятся из конъюнктных или дизъюнктных тетрахордов.

Это частичная таблица суперчастных делений Чалмерса по Хофману. [ кто? ] [4]

Вариации

Романтическая эпоха

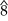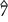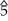Нисходящий тетрахорд в современном B-локрийском ладу (также известный как верхний минорный тетрахорд):8 ступень гаммы– ♭7 ступень гаммы– ♭6 ступень гаммы– ♭5 ступень гаммы(b–a–g–f). Этот тетрахорд охватывает тритон вместо чистой кварты.
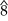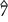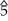Фригийская прогрессия создает нисходящий тетрахорд [5] [ ненадежный источник? ] басовая линия : 8 ступень гаммы– ♭7 ступень гаммы– ♭6 ступень гаммы–5 ступень гаммы. Фригийская половинная каденция : i–v6–iv6–V в до миноре (басовая линия: c–b ♭ –a ♭ –g)

Тетрахорды, основанные на равномерной темперации, использовались для объяснения обычных гептатонических гамм . Приведен следующий словарь тетрахордов (цифры указывают количество полутонов в последовательных интервалах тетрахорда, в сумме дающее пять):

следующие гаммы могут быть получены путем соединения двух тетрахордов с целым тоном (2) между ними: [6] [7]

Все эти гаммы образованы двумя полными дизъюнктными тетрахордами: в отличие от греческой и средневековой теории, тетрахорды здесь изменяются от гаммы к гамме (т. е. тетрахорд C мажор будет C–D–E–F, D мажор D–E–F ♯ –G, C минор C–D–E ♭ –F и т. д.). Теоретики древнегреческой музыки 19 века считали, что это также имело место в античности, и воображали, что существовали дорийские, фригийские или лидийские тетрахорды. Это заблуждение было разоблачено в диссертации Отто Гомбози (1939). [11]

Анализ 20-го века

Теоретики конца 20-го века часто используют термин «тетрахорд» для описания любого набора из четырёх нот при анализе музыки различных стилей и исторических периодов. [12] Выражение «хроматический тетрахорд» может использоваться в двух различных смыслах: для описания особого случая, состоящего из четырёхнотного сегмента хроматической гаммы, [13] или, в более исторически ориентированном контексте, для обозначения шести хроматических нот, используемых для заполнения интервала чистой кварты, обычно встречающегося в нисходящих басовых линиях. [14] Его также можно использовать для описания наборов из менее четырёх нот, когда они используются в стиле гаммы для охвата интервала чистой кварты. [15]

Атональное использование

Аллен Форте иногда использует термин тетрахорд для обозначения того, что он в другом месте называет тетрадой или просто «набором из 4 элементов» — набором из любых четырех высот или классов высот . [16] В теории двенадцати тонов этот термин может иметь особое значение любых четырех последовательных нот ряда из двенадцати тонов. [17]

Незападные весы

Тетрахорды, основанные на равномерно темперированной настройке, также использовались для приближения к обычным гептатоническим гаммам, используемым в индийской, венгерской, арабской и греческой музыке. Западные теоретики 19-го и 20-го веков, убежденные в том, что любая гамма должна состоять из двух тетрахордов и тона, описывали различные комбинации, которые, как предполагалось, соответствовали разнообразию экзотических гамм. Например, следующие диатонические интервалы в один, два или три полутона, всегда составляющие в общей сложности пять полутонов, дают 36 комбинаций, если их соединить целым тоном : [18]

Специфическая индийская система тетрахорда

Тетрахорды, разделенные полутоном , как говорят, также появляются, в частности, в индийской музыке. В этом случае нижний «тетрахорд» составляет шесть полутонов (тритон). Следующие элементы производят 36 комбинаций, когда соединены полутоном. [18] Эти 36 комбинаций вместе с 36 комбинациями, описанными выше, производят так называемые «72 карнатических лада». [19]

персидский

Персидская музыка делит интервал кварты иначе, чем греческая. Например, Аль-Фараби описывает четыре жанра деления кварты: [20]

Он продолжает с четырьмя другими возможными жанрами, «делящими тон на четверти, восьмушки, терции, полутерции, четвертные терции и комбинирующими их различными способами». [21] Позже он представляет возможные положения ладов на лютне, создавая десять интервалов, разделяющих интервал кварты между струнами: [22]

Если учесть, что интервал в кварту между струнами лютни ( уд ) соответствует тетрахорду, и что в октаве есть два тетрахорда и мажорный тон , это создаст 25-тоновую гамму. Более всеобъемлющее описание (где османские, персидские и арабские перекрываются) делений гаммы — это 24 четверти тона (см. также арабский макам ). Следует отметить, что Аль-Фараби, среди других исламских трактатов, также содержал дополнительные схемы деления, а также давал толкование греческой системы, поскольку часто включались доктрины Аристоксена. [23]

Композиционные формы

Тетрахорд, принципиально незаконченный фрагмент, является основой двух композиционных форм, построенных на повторении этого фрагмента: жалобы и ектении.

Нисходящий тетрахорд от тоники до доминанты, обычно в миноре (например, A–G–F–E в A minor), использовался со времен Ренессанса для обозначения плача. Известные случаи включают остинато-бас арии Дидоны When I am laid in earth в Dido and Aeneas Генри Перселла , Crucifixus в Mass in B minor Иоганна Себастьяна Баха , BWV 232, или Qui tollis в Mass in C minor Моцарта , KV 427 и т. д. [24] Этот тетрахорд, известный как lamento («жалоба», «плач»), используется до сих пор. Вариантная форма, полный хроматический спуск (например, A–G ♯ –G–F ♯ –F–E в A minor), был известен как Passus duriusculus в барочном Figurenlehre . [ необходима полная цитата ]

Существует короткая, свободная музыкальная форма эпохи романтизма , называемая жалобой или жалобой (фр.) или плачем . [25] Обычно это набор гармонических вариаций в гомофонической текстуре, в которой бас спускается через некоторый тетрахорд, возможно, тот, что из предыдущего абзаца, но обычно тот, который предполагает минорный лад . Этот тетрахорд, рассматриваемый как очень короткий бас , повторяется снова и снова на протяжении всей композиции.

Другая музыкальная форма того же периода времени — литания или litanie (фр.), или lytanie (OE spur). [26] Это также набор гармонических вариаций в гомофонной фактуре, но в отличие от плача, здесь тетрахордальный фрагмент — восходящий или нисходящий и, возможно, переупорядоченный — установлен в верхнем голосе в манере хоральной прелюдии . Из-за чрезвычайной краткости темы и количества требуемых повторений, а также отсутствия привязки аккордовой прогрессии к тетрахорду в плаче, широта гармонической экскурсии в литании обычно заметна.

Смотрите также

Ссылки

  1. ^ Mathiesen, Thomas J. (2001). "Greece §I: Ancient". В Sadie, S. ; Tyrrell, J. (ред.). The New Grove Dictionary of Music and Musicians (второе изд.). Лондон, Великобритания: Macmillan. 6 Теория музыки, (iii) Аристоксенская традиция, (d) Гаммы.
  2. ↑ Чалмерс 1993, стр. 8.
  3. ↑ Чалмерс 1993, стр. 103.
  4. ↑ Чалмерс 1993, стр. 11.
  5. ^ "Phrygian Progression", Блог классической музыки . Архивировано 2011-10-06 в Wayback Machine
  6. ^ Марсель Дюпре, Cours Complet d'Improvisation a l'Orgue , 2 тома, перевод Джона Фенстермейкера. Париж: Альфонс Ледюк, 1962, 2:35. ASIN: B0006CNH8E.
  7. ^ Джозеф Шиллингер , Система музыкальной композиции Шиллингера , 2 тома. (Нью-Йорк: Карл Фишер, 1941), 1: 112–114. ISBN 978-0306775215 . 
  8. ^ Джошуа Крейг Подольски, Advanced Lead Guitar Concepts (Pacific, Missouri: Mel Bay, 2010): 111. ISBN 978-0-7866-8236-2 . 
  9. ^ "Двойная гармоническая гамма и ее режимы". docs.solfege.org . Архивировано из оригинала 2015-06-18 . Получено 2015-04-12 .
  10. ^ Джонатан Беллман , «Венгерский стиль» в музыке Западной Европы (Бостон: Northeastern University Press, 1993): 120. ISBN 1-55553-169-5 . 
  11. ^ Отто Йоханнес Гомбози, Tonarten und Stimmungen der Antiken Musik , Копенгаген, Эйнар Мунксгаард, 1939.
  12. ↑ Бенедикт Тейлор, «Модальные четырехнотные коллекции высоты тона в музыке американского периода Дворжака », Music Theory Spectrum 32, № 1 (весна 2010 г.): 44–59; Стивен Блок и Джек Даутетт, « Векторные произведения и интервальное взвешивание», Journal of Music Theory 38, № 1 (весна 1994 г.): 21–41; Ян Куинн, «Прослушивание отношений сходства», Perspectives of New Music 39, № 2 (лето 2001 г.): 108–158; Джозеф Н. Штраус, « Стравинский „Построение двенадцати вертикалей“: аспект гармонии в последовательной музыке», Music Theory Spectrum 21, № 1 (весна 1999 г.): 43–73; Tuire Kuusi, «Subset-Class Relation, Common Pitches, and Common Interval Structure Guiding Estimations of Similarity», Music Perception 25, № 1 (сентябрь 2007 г.): 1–11; Joshua B. Mailman , «An Imagined Drama of Competitive Opposition in Carter ’s Scrivo in Vento , With Notes on Narrative, Symmetry, Quantitative Flux and Heraclitus», Music Analysis 28, № 2/3 (июль–октябрь 2009 г.): 373–422; John Harbison и Eleanor Cory , « Martin Boykan : String Quartet (1967): Two Views», Perspectives of New Music 11, № 2 (весна–лето 1973 г.): 204–209; Milton Babbitt , « Edgard Varèse : A Few Observations of His Music», Perspectives of New Music 4, № 2 (весна–лето 1966 г.): 14–22; Annie K. Yih, «Analysing Debussy : Tonality, Motivic Sets and the Referenceential Pitch-Class Specific Collection», Music Analysis 19, № 2 (июль 2000 г.): 203–229; JK Randall , « Composition for Orchestra of Godfrey Winham », Perspectives of New Music 2, № 1 (осень–зима 1963 г.): 102–113.
  13. ^ Брент Ауэрбах, «Многоярусная полифония и ее определяющая роль в фортепианной музыке Иоганнеса Брамса », Журнал теории музыки 52, № 2 (осень 2008 г.): 273–320.
  14. ↑ Роберт Голдин , «Прерванный тетрахорд Бетховена и Седьмая симфония », Integral 5 (1991): 77–100.
  15. ^ Норс С. Джозефсон, «О некоторых очевидных эскизах к Восьмой симфонии Сибелиуса », Archiv für Musikwissenschaft 61, вып. 1 (2004): 54–67.
  16. ^ Аллен Форте (1973). Структура атональной музыки , стр. 1, 18, 68, 70, 73, 87, 88, 21, 119, 123, 124, 125, 138, 143, 171, 174 и 223. Нью-Хейвен и Лондон: Издательство Йельского университета. ISBN 0-300-01610-7 (ткань) ISBN 0-300-02120-8 (бумажная книга). Аллен Форте (1985). "Анализ набора высоты тона сегодня". Анализ музыки 4, №№ 1 и 2 (март–июль: Специальный выпуск: Конференция по анализу музыки Королевского колледжа Лондона 1984): 29–58, цитаты на 48–51, 53.  
  17. ↑ Рейнольд Симпсон, «Новые наброски, старые фрагменты и Третий струнный квартет Шёнберга, соч. 30», Теория и практика 17, В честь Арнольда Шёнберга (1) (1992): 85–101.
  18. ^ ab Марсель Дюпре, Cours Complet d'Improvisation a l'Orgue , 2 тома, перевод Джона Фенстермейкера (Париж: Альфонс Ледюк, 1962): 2:35. ASIN: B0006CNH8E.
  19. ^ Джоанни Гроссе, "Индия. История музыки depuis l'origin jusqu'à nos jours", Encyclopédie de la musique et Dictionnaire du Conservatoire , vol. 1, Париж, Делаграв, 1914, с. 325.
  20. ^ Аль-Фараби 2001, стр. 56–57.
  21. ↑ Аль-Фараби 2001, стр. 58.
  22. ^ Аль-Фараби 2001, стр. 165–179; Либерти Маник, Das Arabische Tonsystem im Mittelalter (Лейден, Э. Дж. Брилл, 1969): 42; Хабиб Хасан Тума , «Музыка арабов » в переводе Лори Шварц. (Портленд, Орегон: Amadeus Press, 1996): 19. ISBN 0-931340-88-8 . 
  23. ↑ Чалмерс 1993, стр. 20.
  24. ↑ Эллен Розанд, «Нисходящий тетрахорд: эмблема плача», The Musical Quarterly 65, № 3 (1979): 346–59.
  25. ^ Марсель Дюпре, Cours complet d'improvisation a l'orgue: Exercices preparées , 2 тома, перевод Джона Фенстермейкера. Париж: Альфонс Ледюк, 1937): 1:14.
  26. ^ Марсель Дюпре, (1962). Cours complet d'improvisation a l'orgue , 2 тома, перевод Джона Фенстермейкера (Париж: Альфонс Ледюк, 1962): 2:110.

Источники

Дальнейшее чтение