
В геометрии набор окружностей Джонсона состоит из трех окружностей одинакового радиуса r, имеющих одну общую точку пересечения H. В такой конфигурации окружности обычно имеют в общей сложности четыре пересечения (точки, где встречаются по крайней мере две из них): общую точку H , которую они все разделяют, и для каждой из трех пар окружностей еще одну точку пересечения (называемую здесь их 2-сторонним пересечением). Если любые две окружности случайно соприкасаются, у них есть только H в качестве общей точки, и тогда будет считаться, что H также является их 2-сторонним пересечением; если они должны совпадать, мы объявляем их 2-сторонним пересечением точку, диаметрально противоположную H. Три точки 2-стороннего пересечения определяют опорный треугольник фигуры. Концепция названа в честь Роджера Артура Джонсона. [1] [2] [3]

Свойство 1 очевидно из определения. Свойство 2 также очевидно: для любой окружности радиуса r и любой точки P на ней окружность радиуса 2 r с центром в точке P касается окружности в ее точке, противоположной P ; это применимо, в частности, к P = H , что дает антикомплементарную окружность C. Свойство 3 в формулировке гомотетии следует немедленно; треугольник точек касания известен как антикомплементарный треугольник.
Для свойств 4 и 5 сначала заметим, что любые две из трех окружностей Джонсона меняются местами при отражении относительно прямой, соединяющей H и их 2-кратное пересечение (или относительно их общей касательной в точке H, если эти точки совпадают), и это отражение также меняет местами две вершины антикомплементарного треугольника, лежащие на этих окружностях. Таким образом, точка 2-кратного пересечения является серединой стороны антикомплементарного треугольника, а H лежит на перпендикуляре к этой стороне. Теперь середины сторон любого треугольника являются образами его вершин при гомотетии с коэффициентом −½, центрированной в барицентре треугольника. Применительно к антикомплементарному треугольнику, который сам получается из треугольника Джонсона гомотетией с коэффициентом 2, из композиции гомотетий следует, что опорный треугольник гомотетичен треугольнику Джонсона с коэффициентом −1. Поскольку такая гомотетия является конгруэнтностью , это дает свойство 5, а также теорему Джонсона об окружностях, поскольку конгруэнтные треугольники имеют описанные окружности одинакового радиуса.
Для свойства 6 уже было установлено, что все перпендикуляры к серединам сторон антикомплементарного треугольника проходят через точку H ; поскольку эта сторона параллельна стороне опорного треугольника, эти перпендикуляры к серединам также являются высотами опорного треугольника.
Свойство 7 немедленно следует из свойства 6, поскольку гомотетический центр, множитель которого равен -1, должен лежать в середине центров описанных окружностей O базового треугольника и H треугольника Джонсона; последний является ортоцентром базового треугольника, и его девятиточечный центр, как известно, является этой средней точкой. Поскольку центральная симметрия также отображает ортоцентр базового треугольника в ортоцентр треугольника Джонсона, гомотетический центр также является девятиточечным центром треугольника Джонсона.
Существует также алгебраическое доказательство теоремы о кругах Джонсона, использующее простое векторное вычисление. Существуют векторы все длины r , такие, что круги Джонсона центрированы соответственно в Тогда точки пересечения по 2 являются соответственно , и точка, очевидно, имеет расстояние r до любой из этих точек пересечения по 2.
Три окружности Джонсона можно считать отражениями описанной окружности исходного треугольника относительно каждой из трех сторон исходного треугольника. Более того, при отражениях относительно трех сторон исходного треугольника его ортоцентр H отображается в три точки на описанной окружности исходного треугольника, которые образуют вершины описанного орто-треугольника , его центр описанной окружности O отображается в вершины треугольника Джонсона, а его прямая Эйлера (прямая, проходящая через O, N, H ) генерирует три прямые, которые пересекаются в точке X (110).
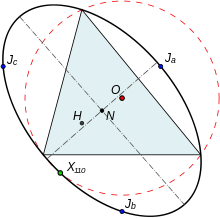
Треугольник Джонсона и его опорный треугольник имеют один и тот же центр из девяти точек, одну и ту же прямую Эйлера и одну и ту же окружность из девяти точек . Шесть точек, образованных вершинами опорного треугольника и его треугольника Джонсона, лежат на окружности Джонсона , центрированной в центре из девяти точек и имеющей точку X (216) опорного треугольника в качестве точки перспективы. Окружность и описанная окружность имеют одну и ту же четвертую точку, X (110) опорного треугольника.
Наконец, есть два интересных и задокументированных описанных куба, которые проходят через шесть вершин исходного треугольника и его треугольника Джонсона, а также через центр описанной окружности, ортоцентр и центр девяти точек. Первый известен как первый куб Муссельмана – K 026. Этот куб также проходит через шесть вершин срединного треугольника и срединный треугольник треугольника Джонсона. Второй куб известен как центральный куб Эйлера – K 044. Этот куб также проходит через шесть вершин ортотреугольника и ортотреугольник треугольника Джонсона.
Обозначение точки X ( i ) соответствует классификации центров треугольников Кларка Кимберлинга ETC.