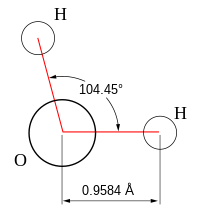
Молекулярная геометрия

Изучение трехмерных форм молекул

Геометрия молекулы воды со значениями длины связи ОН и угла связи HOH между двумя связями

Молекулярная геометрия — это трехмерное расположение атомов , составляющих молекулу . Она включает в себя общую форму молекулы, а также длины связей , углы связей , торсионные углы и любые другие геометрические параметры, которые определяют положение каждого атома.

Молекулярная геометрия влияет на несколько свойств вещества, включая его реакционную способность , полярность , фазу вещества , цвет , магнетизм и биологическую активность . ^{[1] [2] [3]} Углы между связями, которые образует атом, слабо зависят от остальной части молекулы, то есть их можно понимать как приблизительно локальные и, следовательно, переносимые свойства .

Определение

Молекулярная геометрия может быть определена различными спектроскопическими методами и методами дифракции . ИК- , микроволновая и рамановская спектроскопия могут дать информацию о геометрии молекулы из деталей колебательного и вращательного поглощения, обнаруженных этими методами. Рентгеновская кристаллография , нейтронная дифракция и электронная дифракция могут дать молекулярную структуру для кристаллических твердых тел на основе расстояния между ядрами и концентрации электронной плотности. Газовая электронная дифракция может быть использована для малых молекул в газовой фазе. Методы ЯМР и FRET могут быть использованы для определения дополнительной информации, включая относительные расстояния, ^{[4] [5] [6]} двугранные углы, ^{[7] [8]} углы и связность. Молекулярные геометрии лучше всего определяются при низкой температуре, поскольку при более высоких температурах молекулярная структура усредняется по более доступным геометриям (см. следующий раздел). Более крупные молекулы часто существуют в нескольких стабильных геометриях ( конформационная изомерия ), которые близки по энергии на поверхности потенциальной энергии . Геометрии также могут быть вычислены с высокой точностью методами квантовой химии ab initio . Молекулярная геометрия может быть разной в твердом состоянии, в растворе и в виде газа.

Положение каждого атома определяется природой химических связей , которыми он соединен с соседними атомами. Молекулярная геометрия может быть описана положениями этих атомов в пространстве, вызывая длины связей двух соединенных атомов, углы связей трех соединенных атомов и углы кручения ( двугранные углы ) трех последовательных связей.

Влияние теплового возбуждения

Поскольку движения атомов в молекуле определяются квантовой механикой, «движение» должно быть определено квантово-механическим способом. Общие (внешние) квантово-механические движения трансляция и вращение почти не изменяют геометрию молекулы. (В некоторой степени вращение влияет на геометрию через силы Кориолиса и центробежное искажение , но это пренебрежимо мало для настоящего обсуждения.) В дополнение к трансляции и вращению, третьим типом движения является молекулярная вибрация , которая соответствует внутренним движениям атомов, таким как растяжение связей и изменение угла связи. Молекулярные вибрации являются гармоническими (по крайней мере, в хорошем приближении), и атомы колеблются около своих положений равновесия, даже при абсолютном нуле температуры. При абсолютном нуле все атомы находятся в своем основном колебательном состоянии и демонстрируют квантово-механическое движение нулевой точки , так что волновая функция одной колебательной моды не является острым пиком, а приблизительно гауссовой функцией (волновая функция для n  = 0, изображенная в статье о квантовом гармоническом осцилляторе ). При более высоких температурах колебательные моды могут быть термически возбуждены (в классической интерпретации это выражается утверждением, что «молекулы будут вибрировать быстрее»), но они по-прежнему колеблются вокруг узнаваемой геометрии молекулы.

Чтобы оценить вероятность того, что колебание молекулы может быть термически возбуждено, мы рассмотрим фактор Больцмана β ≡ exp(− ⁠Δ Е/кТ⁠ ) ​​, где Δ E — энергия возбуждения колебательной моды, k — постоянная Больцмана ,а T — абсолютная температура. При 298 К (25 °C) типичные значения для фактора Больцмана β составляют:

• β = 0,089 0 для Δ E = 0 500 см ⁻¹
• β = 0,008 0 для Δ E = 1000 см ^-1
• β = 0,0007 для Δ E = 1500 см ^-1 .

( Обратный сантиметр — единица энергии, которая обычно используется в инфракрасной спектроскопии ; 1 см ⁻¹ соответствует1,239 84 × 10−4  эВ ). Когда энергия возбуждения составляет 500 см ⁻¹ , то около 8,9 процентов молекул термически возбуждены при комнатной температуре. Для наглядности: самая низкая энергия возбуждения колебаний в воде — это изгибная мода (около 1600 см ^{− 1} ). Таким образом, при комнатной температуре менее 0,07 процента всех молекул заданного количества воды будут вибрировать быстрее, чем при абсолютном нуле.

Как указано выше, вращение почти не влияет на молекулярную геометрию. Но, как квантово-механическое движение, оно термически возбуждается при относительно (по сравнению с вибрацией) низких температурах. С классической точки зрения можно утверждать, что при более высоких температурах больше молекул будут вращаться быстрее, что подразумевает, что они имеют более высокую угловую скорость и угловой момент . На языке квантовой механики: больше собственных состояний с более высоким угловым моментом становятся термически заселенными с ростом температуры. Типичные энергии вращательного возбуждения составляют порядка нескольких см ⁻¹ . Результаты многих спектроскопических экспериментов расширены, поскольку они включают усреднение по вращательным состояниям. Часто бывает трудно извлечь геометрии из спектров при высоких температурах, поскольку число вращательных состояний, исследованных при экспериментальном усреднении, увеличивается с ростом температуры. Таким образом, можно ожидать, что многие спектроскопические наблюдения дадут надежные молекулярные геометрии только при температурах, близких к абсолютному нулю, поскольку при более высоких температурах слишком много более высоких вращательных состояний термически заселены.

Склеивание

Молекулы, по определению, чаще всего удерживаются вместе с помощью ковалентных связей , включающих одинарные, двойные и/или тройные связи, где «связь» представляет собой общую пару электронов (другой метод связи между атомами называется ионной связью и включает положительный катион и отрицательный анион ).

Молекулярные геометрии могут быть определены в терминах «длины связей», «углов связей» и «торсионных углов». Длина связи определяется как среднее расстояние между ядрами двух атомов, связанных вместе в любой данной молекуле. Угол связи — это угол, образованный между тремя атомами по крайней мере через две связи. Для четырех атомов, связанных вместе в цепочке, торсионный угол — это угол между плоскостью, образованной первыми тремя атомами, и плоскостью, образованной последними тремя атомами.

Существует математическая связь между углами связи для одного центрального атома и четырех периферийных атомов (обозначенных от 1 до 4), выраженная следующим определителем. Это ограничение удаляет одну степень свободы из выбора (первоначально) шести свободных углов связи, оставляя только пять вариантов углов связи. (Углы θ ₁₁ , θ ₂₂ , θ ₃₃ и θ ₄₄ всегда равны нулю, и эта связь может быть изменена для другого числа периферийных атомов путем расширения/сокращения квадратной матрицы.)

${\displaystyle 0={\begin{vmatrix}\cos \theta _{11}&\cos \theta _{12}&\cos \theta _{13}&\cos \theta _{14}\\\cos \theta _{21}&\cos \theta _{22}&\cos \theta _{23}&\cos \theta _{24}\\\cos \theta _{31}&\cos \theta _{32}&\cos \theta _{33}&\cos \theta _{34}\\\cos \theta _{41}&\cos \theta _{42}&\cos \theta _{43}&\cos \theta _{44}\end{vmatrix}}}$

Молекулярная геометрия определяется квантово-механическим поведением электронов. Используя приближение валентных связей , это можно понять по типу связей между атомами, составляющими молекулу. Когда атомы взаимодействуют, образуя химическую связь , говорят, что атомные орбитали каждого атома объединяются в процессе, называемом орбитальной гибридизацией . Два наиболее распространенных типа связей — это сигма-связи (обычно образованные гибридными орбиталями) и пи-связи (образованные негибридизованными p-орбиталями для атомов основных групп элементов ). Геометрию также можно понять с помощью теории молекулярных орбиталей , где электроны делокализованы.

Понимание волнового поведения электронов в атомах и молекулах является предметом квантовой химии .

Изомеры

Изомеры — это типы молекул, которые имеют общую химическую формулу, но различную геометрию, что приводит к разным свойствам:

• Чистое вещество состоит только из одного типа изомеров молекулы (все имеют одинаковую геометрическую структуру).
• Структурные изомеры имеют одинаковую химическую формулу, но различное физическое расположение, часто образуя альтернативные молекулярные геометрии с очень разными свойствами. Атомы не связаны (соединены) вместе в тех же порядках.
  • Функциональные изомеры — это особые виды структурных изомеров, в которых определенные группы атомов демонстрируют особый тип поведения, например, эфир или спирт.
• Стереоизомеры могут иметь много схожих физико-химических свойств (температура плавления, температура кипения) и в то же время очень разную биохимическую активность. Это происходит потому, что они проявляют хиральность , которая обычно встречается в живых системах. Одним из проявлений этой хиральности или хиральности является то, что они обладают способностью вращать поляризованный свет в разных направлениях.
• Сворачивание белков касается сложных геометрических форм и различных изомеров, которые могут принимать белки .

Типы молекулярной структуры

Угол связи — это геометрический угол между двумя соседними связями. Некоторые общие формы простых молекул включают:

• Линейный : В линейной модели атомы соединены по прямой линии. Углы связей установлены на уровне 180°. Например, углекислый газ и оксид азота имеют линейную молекулярную форму.
• Тригонально-плоский : Молекулы с тригонально-плоской формой несколько треугольные и находятся в одной плоскости (плоские) . Следовательно, углы связи устанавливаются на уровне 120°. Например, трифторид бора .
• Угловой : Угловые молекулы (также называемые изогнутыми или V-образными ) имеют нелинейную форму. Например, вода (H2O ₎ , которая имеет угол около 105°. Молекула воды имеет две пары связанных электронов и две неподеленные неподеленные пары электронов.
• Тетраэдрический : Тетра- означает четыре, а -эдрический относится к грани твердого тела, поэтому « тетраэдрический » буквально означает «имеющий четыре грани». Эта форма встречается, когда на одном центральном атоме находятся четыре связи , без дополнительных неподеленных электронных пар. В соответствии с VSEPR (теорией отталкивания электронных пар валентной оболочки), углы связи между электронными связями равны arccos (− ⁠1/3⁠ ) ​​= 109,47°. Например, метан (CH ₄ ) — тетраэдрическая молекула.
• Октаэдрический : Окта- означает восемь, а -эдрический относится к грани твердого тела, поэтому « октаэдрический » означает «имеющий восемь граней». Угол связи составляет 90 градусов. Например, гексафторид серы (SF6 ₎ является октаэдрической молекулой.
• Тригональная пирамидальная : Молекула тригональной пирамиды имеет пирамидообразную форму с треугольным основанием. В отличие от линейных и тригональных плоских форм, но схожих с тетраэдрической ориентацией, пирамидальные формы требуют трех измерений для полного разделения электронов. Здесь есть только три пары связанных электронов, оставляя одну неподеленную неподеленную пару. Отталкивания неподеленной пары — пары связей изменяют угол связи с тетраэдрического угла на немного меньшее значение. ^[9] Например, аммиак (NH ₃ ).

Таблица ВСЕПР

Углы связей в таблице ниже являются идеальными углами из простой теории VSEPR (произносится как «теория Веспера») ^{[ требуется ссылка ]} , за которыми следует фактический угол для примера, приведенного в следующей колонке, где он отличается. Для многих случаев, таких как тригональная пирамида и изогнутая, фактический угол для примера отличается от идеального угла, и примеры отличаются на разную величину. Например, угол в H ₂ S (92°) отличается от тетраэдрического угла намного больше, чем угол для H ₂ O (104,48°).

3D-изображения

• Линия или палка – атомные ядра не представлены, только связи в виде палок или линий. Как и в двумерных молекулярных структурах этого типа, атомы подразумеваются в каждой вершине.

• График электронной плотности – показывает электронную плотность, определенную либо кристаллографически , либо с использованием квантовой механики, а не отдельных атомов или связей.

• Шар и палочка – атомные ядра представлены сферами (шариками), а связи – палочками.

• Модели заполнения пространства или модели CPK (также схема атомной окраски в представлениях) – молекула представлена ​​перекрывающимися сферами, представляющими атомы.

• Мультфильм – представление, используемое для белков, в котором петли, бета-слои и альфа-спирали представлены схематически, а атомы или связи явно не представлены (например, остов белка представлен в виде гладкой трубы).

Чем больше неподеленных пар содержится в молекуле, тем меньше углы между атомами этой молекулы. Теория VSEPR предсказывает, что неподеленные пары отталкиваются друг от друга, тем самым отталкивая от себя различные атомы.

Смотрите также

• Джеммис mno правила
• структура Льюиса
• Программное обеспечение для молекулярного дизайна
• Молекулярная графика
• Молекулярная механика
• Молекулярное моделирование
• Молекулярная симметрия
• Редактор молекул
• Теория полиэдральных скелетных электронных пар
• Квантовая химия
• Ленточная диаграмма
• Правило Стикса (для бороводородов)
• Топология (химия)

Ссылки

1. Макмарри, Джон Э. (1992), Органическая химия (3-е изд.), Belmont: Wadsworth, ISBN 0-534-16218-5
2. Коттон, Ф. Альберт ; Уилкинсон, Джеффри ; Мурильо, Карлос А.; Бохманн, Манфред (1999), Advanced Inorganic Chemistry (6-е изд.), Нью-Йорк: Wiley-Interscience, ISBN 0-471-19957-5
3. Александрос Хремос; Джек Ф. Дуглас (2015). «Когда разветвленный полимер становится частицей?». J. Chem. Phys . 143 (11): 111104. Bibcode : 2015JChPh.143k1104C. doi : 10.1063/1.4931483 . PMID  26395679.
4. Описание FRET Архивировано 18 сентября 2008 г. на Wayback Machine
5. Хиллиш, А.; Лоренц, М.; Дикманн, С. (2001). «Последние достижения в области FRET: определение расстояния в комплексах белок–ДНК». Current Opinion in Structural Biology . 11 (2): 201–207. doi :10.1016/S0959-440X(00)00190-1. PMID  11297928.
6. Введение в визуализацию FRET Архивировано 14 октября 2008 г. на Wayback Machine
7. получение двугранных углов из констант связи 3J Архивировано 2008-12-07 на Wayback Machine
8. Еще одна константа связи ЯМР с двугранным углом, подобная Javascript. Архивировано 28 декабря 2005 г. на Wayback Machine.
9. Мисслер ГЛ и Тарр Д.А. Неорганическая химия (2-е изд., Prentice-Hall 1999), стр.57-58
10. Хейнс, Уильям М., ред. (2013). CRC Handbook of Chemistry and Physics (94-е изд.). CRC Press . стр. 9–26. ISBN 9781466571143.
11. Хой, AR; Банкер, PR (1979). «Точное решение уравнения Шредингера с изгибом вращения для трехатомной молекулы с применением к молекуле воды». Журнал молекулярной спектроскопии . 74 (1): 1–8. Bibcode : 1979JMoSp..74....1H. doi : 10.1016/0022-2852(79)90019-5.
12. "CCCBDB Experimental bond angles page 2". Архивировано из оригинала 2014-09-03 . Получено 2014-08-27 .

Внешние ссылки

• Учебное пособие по молекулярной геометрии и полярности. 3D-визуализация молекул для определения полярности.
• Молекулярная геометрия с использованием кристаллов. Трехмерная визуализация структуры молекул с использованием кристаллографии.