
Фазовая диаграмма в физической химии , инжиниринге , минералогии и материаловедении — это тип диаграммы, используемой для отображения условий (давление, температура и т. д.), при которых термодинамически различные фазы (например, твёрдое, жидкое или газообразное состояние) возникают и сосуществуют в равновесии .
Обычными компонентами фазовой диаграммы являются линии равновесия или границы фаз , которые относятся к линиям, отмечающим условия, при которых несколько фаз могут сосуществовать в равновесии. Фазовые переходы происходят вдоль линий равновесия. Метастабильные фазы не показаны на фазовых диаграммах, поскольку, несмотря на их распространенность, они не являются равновесными фазами.
Тройные точки — это точки на фазовых диаграммах, где пересекаются линии равновесия. Тройные точки отмечают условия, при которых могут сосуществовать три различные фазы. Например, на фазовой диаграмме воды есть тройная точка, соответствующая одной температуре и давлению, при которых твердая, жидкая и газообразная вода могут сосуществовать в устойчивом равновесии (273,16 К и парциальное давление пара611,657 Па ). Давление на диаграмме давление-температура (такой как показанная диаграмма фаз воды) является парциальным давлением рассматриваемого вещества. [1]
Солидус — это температура, ниже которой вещество стабильно в твердом состоянии. Ликвидус — это температура, выше которой вещество стабильно в жидком состоянии. Между солидусом и ликвидусом может быть зазор; внутри зазора вещество состоит из смеси кристаллов и жидкости (как « суспензия »). [2]
Рабочие жидкости часто классифицируют на основе формы их фазовой диаграммы.

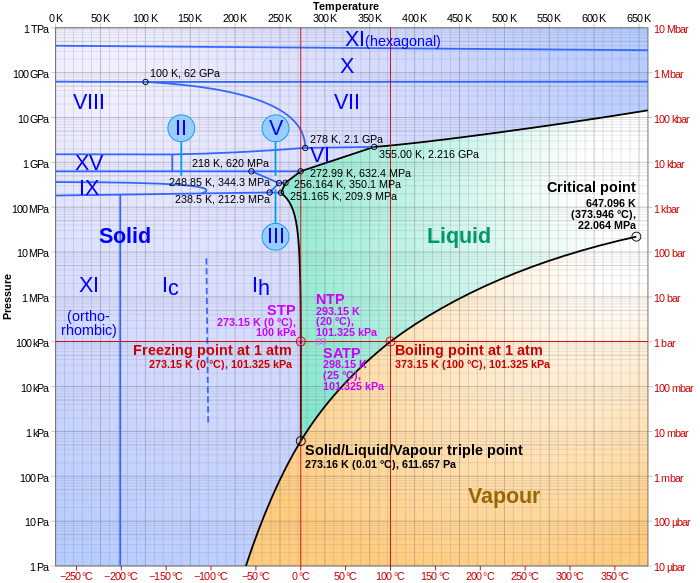
Простейшие фазовые диаграммы — это диаграммы давление–температура одного простого вещества, такого как вода . Оси соответствуют давлению и температуре . Фазовая диаграмма показывает в пространстве давление–температура линии равновесия или фазовые границы между тремя фазами: твердым телом , жидкостью и газом .
Кривые на фазовой диаграмме показывают точки, в которых свободная энергия (и другие производные свойства) становятся неаналитическими: их производные по координатам (температура и давление в данном примере) изменяются скачкообразно (резко). Например, теплоемкость контейнера, заполненного льдом, будет резко меняться по мере нагревания контейнера выше точки плавления. Открытые пространства, где свободная энергия аналитична , соответствуют однофазным областям. Однофазные области разделены линиями неаналитического поведения, где происходят фазовые переходы , которые называются фазовыми границами .
На диаграмме справа фазовая граница между жидкостью и газом не продолжается бесконечно. Вместо этого она заканчивается в точке на фазовой диаграмме, называемой критической точкой . Это отражает тот факт, что при чрезвычайно высоких температурах и давлениях жидкая и газообразная фазы становятся неразличимыми, [3] в том, что известно как сверхкритическая жидкость . В воде критическая точка находится около T c = 647,096 K (373,946 °C), p c = 22,064 МПа (217,75 атм) и ρ c = 356 кг/м 3 . [4]
Существование критической точки жидкость–газ выявляет небольшую двусмысленность в маркировке областей одной фазы. При переходе из жидкой в газообразную фазу обычно пересекают границу фаз, но можно выбрать путь, который никогда не пересекает границу, идя вправо от критической точки. Таким образом, жидкая и газообразная фазы могут непрерывно смешиваться друг с другом. Граница фаз твердое тело–жидкость может заканчиваться в критической точке только в том случае, если твердая и жидкая фазы имеют одну и ту же группу симметрии . [5]
Для большинства веществ граница раздела фаз твердое тело-жидкость (или кривая плавления) на фазовой диаграмме имеет положительный наклон , так что температура плавления увеличивается с давлением. Это справедливо всякий раз, когда твердая фаза плотнее жидкой фазы. [6] Чем больше давление на данное вещество, тем ближе друг к другу располагаются молекулы вещества, что увеличивает эффект межмолекулярных сил вещества . Таким образом, веществу требуется более высокая температура, чтобы его молекулы имели достаточно энергии, чтобы вырваться из фиксированной структуры твердой фазы и войти в жидкую фазу. Аналогичная концепция применима к фазовым переходам жидкость-газ. [7]
Вода является исключением, поскольку имеет границу твердого тела и жидкости с отрицательным наклоном, так что точка плавления уменьшается с давлением. Это происходит потому, что лед (твердая вода) менее плотный, чем жидкая вода, о чем свидетельствует тот факт, что лед плавает на воде. На молекулярном уровне лед менее плотный, поскольку он имеет более обширную сеть водородных связей , которая требует большего разделения молекул воды. [6] Другие исключения включают сурьму и висмут . [8] [9]
При очень высоких давлениях выше 50 ГПа (500 000 атм) жидкий азот претерпевает фазовый переход жидкость-жидкость в полимерную форму и становится плотнее, чем твердый азот при том же давлении. Поэтому в этих условиях твердый азот также плавает в своей жидкости. [10]
Значение наклона d P /d T определяется уравнением Клаузиуса–Клапейрона для плавления [11]
где Δ H fus — теплота плавления, которая всегда положительна, а Δ V fus — изменение объема при плавлении. Для большинства веществ Δ V fus положительно, поэтому наклон положительный. Однако для воды и других исключений Δ V fus отрицательно, поэтому наклон отрицательный.
В дополнение к температуре и давлению, другие термодинамические свойства могут быть изображены на фазовых диаграммах. Примерами таких термодинамических свойств являются удельный объем , удельная энтальпия или удельная энтропия . Например, однокомпонентные графики температуры против удельной энтропии ( T против s ) для воды/ пара или для хладагента обычно используются для иллюстрации термодинамических циклов, таких как цикл Карно , цикл Ренкина или цикл парокомпрессионного охлаждения .
Любые две термодинамические величины могут быть показаны на горизонтальной и вертикальной осях двумерной диаграммы. Дополнительные термодинамические величины могут быть проиллюстрированы в виде серии линий — изогнутых, прямых или комбинации изогнутых и прямых. Каждая из этих изолиний представляет термодинамическую величину при определенном постоянном значении.

Можно представить трехмерные (3D) графики, показывающие три термодинамические величины. [12] [13] Например, для одного компонента трехмерный график типа декартовых координат может показывать температуру ( T ) на одной оси, давление ( p ) на второй оси и удельный объем ( v ) на третьей. Такой трехмерный график иногда называют диаграммой p – v – T. Условия равновесия показаны в виде кривых на изогнутой поверхности в 3D с областями для твердой, жидкой и паровой фаз и областями, где твердое тело и жидкость, твердое тело и пар или жидкость и пар сосуществуют в равновесии. Линия на поверхности, называемая тройной линией, находится там, где твердое тело, жидкость и пар могут сосуществовать в равновесии. Критическая точка остается точкой на поверхности даже на трехмерной фазовой диаграмме.
Ортографическая проекция трехмерного графика p – v – T , показывающая давление и температуру как вертикальную и горизонтальную оси, сворачивает трехмерный график в стандартную двумерную диаграмму давление–температура. Когда это сделано, поверхности твердое тело–пар, твердое тело–жидкость и жидкость–пар сворачиваются в три соответствующие кривые линии, встречающиеся в тройной точке, которая является свернутой ортографической проекцией тройной линии.
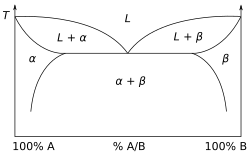
Могут быть построены и другие, гораздо более сложные типы фазовых диаграмм, особенно когда присутствует более одного чистого компонента. В этом случае концентрация становится важной переменной. Могут быть построены фазовые диаграммы с более чем двумя измерениями, которые показывают влияние более двух переменных на фазу вещества. Фазовые диаграммы могут использовать другие переменные в дополнение к температуре, давлению и составу или вместо них, например, силу приложенного электрического или магнитного поля, и они также могут включать вещества, которые принимают более трех состояний вещества. Один тип фазовой диаграммы отображает температуру против относительных концентраций двух веществ в бинарной смеси, называемой бинарной фазовой диаграммой , как показано справа. Такая смесь может быть либо твердым раствором , эвтектической или перитектической , среди прочих. Эти два типа смесей приводят к очень разным графикам. Другой тип бинарной фазовой диаграммы — это диаграмма точек кипения для смеси двух компонентов, т. е. химических соединений . Для двух конкретных летучих компонентов при определенном давлении, таком как атмосферное давление , диаграмма точек кипения показывает, какие составы пара (газа) находятся в равновесии с заданными составами жидкости в зависимости от температуры. На типичной бинарной диаграмме точек кипения температура откладывается на вертикальной оси, а состав смеси — на горизонтальной оси.

Показана двухкомпонентная диаграмма с компонентами A и B в «идеальном» растворе. Построение диаграммы фаз жидкость-пар предполагает идеальный жидкий раствор, подчиняющийся закону Рауля , и идеальную газовую смесь, подчиняющуюся закону Дальтона парциального давления . Линия связи от жидкости к газу при постоянном давлении будет указывать на два состава жидкости и газа соответственно. [14]
Простой пример диаграммы с гипотетическими компонентами 1 и 2 в неазеотропной смеси показан справа. Тот факт, что существуют две отдельные кривые линии, соединяющие точки кипения чистых компонентов, означает, что состав пара обычно не совпадает с составом жидкости, с которой пар находится в равновесии. Для получения дополнительной информации см. Равновесие пар-жидкость .
В дополнение к вышеупомянутым типам фазовых диаграмм, существует множество других возможных комбинаций. Некоторые из основных особенностей фазовых диаграмм включают конгруэнтные точки, где твердая фаза превращается непосредственно в жидкость. Существует также перитектоид , точка, где две твердые фазы объединяются в одну твердую фазу при охлаждении. Обратное этому, когда одна твердая фаза превращается в две твердые фазы при охлаждении, называется эвтектоидом .
Сложную фазовую диаграмму, имеющую большое технологическое значение, представляет собой диаграмма системы железо – углерод при содержании углерода менее 7% (см. сталь ).
Ось x такой диаграммы представляет собой переменную концентрации смеси. Поскольку смеси обычно далеки от разбавления, а их плотность как функция температуры обычно неизвестна, предпочтительной мерой концентрации является мольная доля . Объемная мера, такая как молярность, была бы нецелесообразной.
Система с тремя компонентами называется тройной системой. При постоянном давлении максимальное число независимых переменных равно трем — температуре и двум значениям концентрации. Для представления тройных равновесий требуется трехмерная фазовая диаграмма. Часто такую диаграмму рисуют с составом в виде горизонтальной плоскости и температурой на оси, перпендикулярной этой плоскости. Для представления состава в тройной системе используют равносторонний треугольник, называемый треугольником Гиббса (см. также Тройной график ).
Шкала температур откладывается на оси, перпендикулярной треугольнику состава. Таким образом, пространственная модель тройной фазовой диаграммы представляет собой прямоугольную призму. Стороны призмы представляют соответствующие двойные системы AB, BC, AC.
Однако наиболее распространенными методами представления фазовых равновесий в тройной системе являются следующие: 1) проекции на концентрационный треугольник ABC поверхностей ликвидуса, солидуса, сольвуса; 2) изотермические сечения; 3) вертикальные сечения. [15]
Полиморфные и полиаморфные вещества имеют несколько кристаллических или аморфных фаз, которые можно графически изобразить аналогично твердым, жидким и газообразным фазам.
Некоторые органические материалы проходят через промежуточные состояния между твердым и жидким; эти состояния называются мезофазами . Внимание было направлено на мезофазы, поскольку они позволяют использовать устройства отображения и стали коммерчески важными благодаря так называемой жидкокристаллической технологии. Фазовые диаграммы используются для описания возникновения мезофаз. [17]