Хорошо покрытый граф

В теории графов хорошо покрытый граф — это неориентированный граф , в котором минимальные вершинные покрытия имеют одинаковый размер. Здесь вершинное покрытие — это множество вершин, которое касается всех ребер, и оно минимально, если удаление любой вершины из него оставит некоторое ребро непокрытым. Эквивалентно, хорошо покрытые графы — это графы, в которых все максимальные независимые множества имеют одинаковый размер. Хорошо покрытые графы были определены и впервые изучены Майклом Д. Пламмером в 1970 году.

Хорошо покрытые графы включают все полные графы , сбалансированные полные двудольные графы и ладейные графы , вершины которых представляют клетки шахматной доски, а ребра — ходы шахматной ладьи. Известные характеристики хорошо покрытых кубических графов , хорошо покрытых графов без клешней и хорошо покрытых графов с большим обхватом позволяют распознавать эти графы за полиномиальное время , но проверка того, являются ли другие виды графов хорошо покрытыми, является coNP-полной задачей.

Определения

Вершинное покрытие в неориентированном графе — это набор вершин, который касается каждого ребра в графе. Вершинное покрытие является минимальным или неизбыточным, если удаление любой вершины из него разрушит свойство покрытия: удаление приведет к тому, что некоторое ребро станет непокрытым. Оно является минимальным, если нет другого вершинного покрытия с меньшим количеством вершин. Хорошо покрытый граф — это тот, в котором каждое минимальное покрытие также является минимальным. В оригинальной статье, определяющей хорошо покрытый граф, Пламмер пишет, что это «очевидно эквивалентно» свойству, что любые два минимальных покрытия имеют одинаковое количество вершин. ^[1]

Независимое множество в графе — это множество вершин, никакие две из которых не являются смежными. Если $C$ — вершинное покрытие в графе $G$ , дополнение C должно быть независимым множеством, и наоборот. $C$ является минимальным вершинным покрытием тогда и только тогда, когда его дополнение $I$ является максимальным независимым множеством, а $C является минимальным вершинным покрытием тогда и только тогда, когда$ $его$ дополнение является максимальным независимым множеством. Поэтому хорошо покрытый граф — это, что эквивалентно, граф, в котором каждое максимальное независимое множество имеет одинаковый размер, или граф, в котором каждое максимальное независимое множество является максимальным. ^[2]

В оригинальной статье, определяющей хорошо покрытые графы, эти определения были ограничены связными графами , ^[3] хотя они имеют смысл и для несвязных графов. Некоторые более поздние авторы заменили требование связности более слабым требованием, что хорошо покрытые графы не должны иметь изолированных вершин. ^[4] Как для связных хорошо покрытых графов, так и для хорошо покрытых графов без изолированных вершин не может быть существенных вершин , вершин, которые принадлежат каждому минимальному вершинному покрытию. Кроме того, каждый хорошо покрытый граф является критическим графом для вершинного покрытия в том смысле, что для каждой вершины $v$ удаление $v$ из графа дает граф с меньшим минимальным вершинным покрытием. ^[3]

Комплекс независимости графа $G$ — это симплициальный комплекс, имеющий симплекс для каждого независимого множества в $G.$ Симплициальный комплекс называется чистым, если все его максимальные симплексы имеют одинаковую мощность, поэтому хорошо покрытый граф эквивалентно является графом с чистым комплексом независимости. ^[5]

Примеры

Неатакующее размещение восьми ладей на шахматной доске. Если на шахматной доске размещено менее восьми ладей неатакующим образом, их всегда можно расширить до восьми ладей, которые останутся неатакующими.

Граф цикла длины четыре или пять хорошо покрыт: в каждом случае каждое максимальное независимое множество имеет размер два. Цикл длины семь и путь длины три также хорошо покрыты. ^[6] Каждый полный граф хорошо покрыт: каждое максимальное независимое множество состоит из одной вершины. Аналогично, каждый кластерный граф (несвязное объединение полных графов) хорошо покрыт. ^[7] Полный двудольный граф хорошо покрыт, если две стороны его двудольного разделения имеют одинаковое количество вершин, поскольку это его единственные два максимальных независимых множества. Дополнительный граф графа без треугольников без изолированных вершин хорошо покрыт: он не имеет независимых множеств больше двух, и каждая отдельная вершина может быть расширена до независимого множества из двух вершин. ^[6]

Граф ладьи хорошо покрыт: если разместить любой набор ладей на шахматной доске так, чтобы никакие две ладьи не атаковали друг друга, всегда можно продолжать размещать больше неатакующих ладей, пока не будет по одной в каждой строке и столбце шахматной доски. ^[8] Граф, вершины которого являются диагоналями простого многоугольника , а ребра соединяют пары диагоналей, которые пересекаются друг с другом, хорошо покрыт, потому что его максимальные независимые множества являются триангуляциями многоугольника, и все триангуляции имеют одинаковое количество ребер. ^[9]

Если $G$ — любой граф $с n$ вершинами, то корневое произведение $G$ с графом с одним ребром (то есть граф $H$ , образованный добавлением $n$ новых вершин к $G$ , каждая из которых имеет степень один и каждая смежна с отдельной вершиной в $G$ ), является хорошо покрытым. Действительно, максимальное независимое множество в $H$ должно состоять из произвольного независимого множества в $G$ вместе с соседями степени один дополнительного множества и, следовательно, должно иметь размер $n$ . ^[10] В более общем случае, если задан любой граф $G$ вместе с покрытием клик (разбиением $p$ вершин графа $G$ на клики), граф $G p$ , образованный добавлением еще одной вершины к каждой клике, является хорошо покрытым; корневое произведение является частным случаем этой конструкции, когда $p$ состоит из $n$ клик с одной вершиной. ^[11] Таким образом, каждый граф является индуцированным подграфом хорошо покрытого графа.

Двудольность, очень хорошо покрытые графы и обхват

Фаварон (1982) определяет очень хорошо покрытый граф как хорошо покрытый граф (возможно, несвязный, но без изолированных вершин), в котором каждое максимальное независимое множество (и, следовательно, также каждое минимальное вершинное покрытие) содержит ровно половину вершин. Это определение включает корневые произведения графа $G$ и однореберного графа. Оно также включает, например, двудольные хорошо покрытые графы, изученные Равиндрой (1977) и Берже (1981): в двудольном графе без изолированных вершин обе стороны любого двудольного графа образуют максимальные независимые множества (и минимальные вершинные покрытия), поэтому, если граф хорошо покрытый, обе стороны должны иметь одинаковое количество вершин. В хорошо покрытом графе с $n$ вершинами, без изолированных вершин, размер максимального независимого множества не превышает $n /2$ , поэтому очень хорошо покрытые графы — это хорошо покрытые графы, в которых максимальный размер независимого множества максимально велик. ^[12]

Двудольный граф $G$ хорошо покрыт тогда и только тогда, когда он имеет совершенное паросочетание $M$ со следующим свойством: для каждого ребра $uv$ в $M$ индуцированный подграф соседей $u$ и $v$ образует полный двудольный граф . ^[13] Характеристика в терминах паросочетаний может быть расширена с двудольных графов на очень хорошо покрытые графы: граф $G$ очень хорошо покрыт тогда и только тогда, когда он имеет совершенное паросочетание $M$ со следующими двумя свойствами:

Ни одно ребро $M$ не принадлежит треугольнику в $G$ , и
Если ребро $M$ является центральным ребром трехреберного пути в $G$ , то две конечные точки пути должны быть смежными.

Более того, если $G$ очень хорошо покрыт, то каждое совершенное паросочетание в $G$ удовлетворяет этим свойствам. ^[14]

Деревья являются частным случаем двудольных графов, и проверка того, является ли дерево хорошо покрытым, может быть обработана как гораздо более простой частный случай характеризации хорошо покрытых двудольных графов: если $G$ является деревом с более чем двумя вершинами, оно хорошо покрытое тогда и только тогда, когда каждый нелистовой узел дерева смежн ровно с одним листом. ^[13] Та же самая характеризация применима к графам, которые локально древовидны, в том смысле, что окрестности с малым диаметром каждой вершины являются ациклическими: если граф имеет обхват восемь или более (так что для каждой вершины $v$ подграф вершин в пределах расстояния три от $v$ является ациклическим), то он хорошо покрыт тогда и только тогда, когда каждая вершина степени больше единицы имеет ровно одного соседа степени один. ^[15] Тесно связанная, но более сложная характеризация применима к хорошо покрытым графам обхвата пять или более. ^[16]

Регулярность и планарность

Кубические ( 3-регулярные ) хорошо покрытые графы были классифицированы: они состоят из семи 3 -связных примеров, а также трех бесконечных семейств кубических графов с меньшей связностью. ^[17]

Семь 3-связных кубических хорошо покрытых графов — это полный граф $K 4$ , графы треугольной призмы и пятиугольной призмы , граф Дюрера , граф полезности $K 3,3$ , граф с восемью вершинами, полученный из графа полезности с помощью преобразования Y-Δ , и 14-вершинный обобщенный граф Петерсена $G (7,2)$ . ^[18] Из этих графов первые четыре являются планарными графами . Это единственные четыре кубических полиэдральных графа (графы простых выпуклых многогранников ), которые хорошо покрыты. ^[19] Четыре из графов (две призмы, граф Дюрера и $G (7,2)$ ) являются обобщенными графами Петерсена.

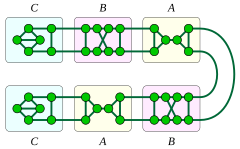
Все 1- и 2-связные кубические хорошо покрытые графы образованы путем замены узлов пути или цикла тремя фрагментами графов, которые Пламмер (1993) обозначил как $A$ , $B$ и $C.$ Фрагменты $A$ или $B$ могут быть использованы для замены узлов цикла или внутренних узлов пути, в то время как фрагмент $C$ используется для замены двух конечных узлов пути. Фрагмент $A$ содержит мост , поэтому результатом выполнения этого процесса замены на пути и использования фрагмента $A$ для замены некоторых узлов пути (и двух других фрагментов для оставшихся узлов) является 1-вершинно-связный кубический хорошо покрытый граф. Все 1-вершинно-связные кубические хорошо покрытые графы имеют эту форму, и все такие графы являются планарными. ^[17]

Существует два типа 2-вершинно-связных кубических хорошо покрытых графов. Одно из этих двух семейств образуется путем замены узлов цикла фрагментами $A$ и $B$ , причем по крайней мере два из фрагментов имеют тип $A$ ; граф этого типа является планарным тогда и только тогда, когда он не содержит фрагментов типа $B.$ Другое семейство образуется путем замены узлов пути фрагментами типа $B$ и $C$ ; все такие графы являются планарными. ^[17]

Дополняя характеристику хорошо покрытых простых многогранников в трех измерениях, исследователи также рассмотрели хорошо покрытые симплициальные многогранники или, что эквивалентно, хорошо покрытые максимальные планарные графы. Каждый максимальный планарный граф с пятью или более вершинами имеет вершинную связность 3, 4 или 5. ^[20] Не существует хорошо покрытых 5-связных максимальных планарных графов, и есть только четыре 4-связных хорошо покрытых максимальных планарных графа: графы правильного октаэдра , пентагональной дипирамиды , плосконосого двуклиноида и неправильного многогранника (невыпуклого дельтаэдра ) с 12 вершинами, 30 ребрами и 20 треугольными гранями. Однако существует бесконечно много 3-связных хорошо покрытых максимальных планарных графов. ^[21] Например, если $3 t$ -вершинный максимальный планарный граф имеет $t$ непересекающихся треугольных граней, то эти грани образуют покрытие кликой. Следовательно, построение покрытия кликой, которое для этих графов состоит из подразделения каждого из этих $t$ треугольников на три новых треугольника, встречающихся в центральной вершине, производит хорошо покрытый максимальный планарный граф. ^[22]

Сложность

Проверка того, содержит ли граф два максимальных независимых множества разных размеров, является NP-полной ; то есть, дополнительно, проверка того, является ли граф хорошо покрытым, является coNP-полной. ^[23] Хотя легко найти максимальные независимые множества в графах, которые известны как хорошо покрытые, для алгоритма также NP-сложно производить в качестве выходных данных для всех графов либо максимальное независимое множество, либо гарантию того, что входные данные не являются хорошо покрытыми. ^[24]

Напротив, можно проверить, является ли заданный граф $G$ очень хорошо покрытым, за полиномиальное время . Для этого найдите подграф $H$ графа $G$ , состоящий из ребер, которые удовлетворяют двум свойствам сопоставленного ребра в очень хорошо покрытом графе, а затем используйте алгоритм сопоставления, чтобы проверить, имеет ли $H$ идеальное сопоставление. ^[14] Некоторые задачи, которые являются NP-полными для произвольных графов, такие как задача нахождения гамильтонова цикла , также могут быть решены за полиномиальное время для очень хорошо покрытых графов. ^[25]

Граф называется эквипарным, если каждое максимальное паросочетание является максимальным; то есть он эквипарным, если его линейный граф хорошо покрыт. ^[26] Более строго он называется случайно парным , если каждое максимальное паросочетание является идеальным паросочетанием . Единственными связанными случайно парными графами являются полные графы и сбалансированные полные двудольные графы. ^[27] Можно проверить, является ли линейный граф или, в более общем случае, граф без клешней , хорошо покрытым за полиномиальное время. ^[28]

Характеристика хорошо покрытых графов с обхватом пять или более, а также хорошо покрытых графов, которые являются 3-регулярными, также приводит к эффективным алгоритмам полиномиального времени для распознавания этих графов. ^[29]

Примечания

^ Пламмер (1970). Пламмер использует «точку» для обозначения вершины в графе, «линию» для обозначения ребра и «покрытие точек» для обозначения покрытия вершин; эта терминология вышла из употребления.
^ Пламмер (1993).
^ ab Plummer (1970).
^ Фаварон (1982).
^ Примеры статей, использующих эту терминологию, см. в Dochtermann & Engström (2009) и Cook & Nagel (2010).
^ ab Sankaranarayana (1994), раздел 2.4, «Примеры», стр. 7.
^ Холройд и Талбот (2005).
^ Графы ладьи, эквивалентно, являются линейными графами полных двудольных графов, поэтому хорошо изученное свойство графов ладьи эквивалентно тому факту, что полные двудольные графы являются равнопарными, о чем см. Самнер (1979) и Леск, Пламмер и Пуллибланк (1984).
^ Гринберг (1993).
^ Этот класс примеров изучался Финком и др. (1985); они также (вместе с циклом из четырех ребер, который также хорошо покрыт) являются в точности графами, число доминирования которых равно $n / 2.$ Его свойство хорошо покрывать также сформулировано в другой терминологии (имея чистый комплекс независимости) как теорема 4.4 Дохтерманна и Энгстрёма (2009).
^ Для построения покрытия кликой см. Кук и Нагель (2010), Лемма 3.2. Этот источник излагает свои результаты в терминах чистоты комплекса независимости и использует термин «полностью усатый» для особого случая корневого произведения.
^ Берге (1981).
^ ab Равиндра (1977); Пламмер (1993).
^ ab Staples (1975); Фаварон (1982); Пламмер (1993).
^ Финбоу и Хартнелл (1983); Пламмер (1993), Теорема 4.1.
^ Финбоу и Хартнелл (1983); Пламмер (1993), Теорема 4.2.
^ abc Кэмпбелл (1987); Кэмпбелл и Пламмер (1988); Пламмер (1993).
^ Кэмпбелл (1987); Финбоу, Хартнелл и Новаковски (1988); Кэмпбелл, Эллингем и Ройл (1993); Пламмер (1993).
^ Кэмпбелл и Пламмер (1988).
^ Все полные графы с 1, 2, 3 и 4 вершинами являются максимально планарными и хорошо покрытыми; их вершинная связность либо неограничена, либо не превышает трех, в зависимости от деталей определения вершинной связности, которые не имеют значения для больших максимальных планарных графов.
^ Финбоу, Хартнелл и Новаковски и др. (2003, 2009, 2010).
^ Графы, построенные таким образом, называются -семейством по мнению Финбоу и др. (2016); дополнительные примеры могут быть построены с помощью операции, которую они называют O-соединением для объединения меньших графов. $К_{4}$
^ Шанкаранараяна и Стюарт (1992); Хватал и Слейтер (1993); Каро, Себо и Тарси (1996).
^ Рагхаван и Спинрад (2003).
^ Шанкаранараяна и Стюарт (1992).
↑ Леск, Пламмер и Пуллибланк (1984).
^ Самнер (1979).
^ Леск, Пламмер и Пуллибланк (1984); Танкус и Тарси (1996); Танкус и Тарси (1997).
^ Кэмпбелл, Эллингем и Ройл (1993); Пламмер (1993).

Ссылки

Берже, Клод (1981), «Некоторые общие свойства регуляризуемых графов, рёберно-критических графов и $B$ -графов», Теория графов и алгоритмы (Proc. Sympos., Res. Inst. Electr. Comm., Tohoku Univ., Sendai, 1980) , Lecture Notes in Computer Science, т. 108, Берлин: Springer, стр. 108–123, doi : 10.1007/3-540-10704-5_10 , ISBN 978-3-540-10704-0, МР 0622929.
Кэмпбелл, SR (1987), Некоторые результаты о плоских хорошо покрытых графах , докторская диссертация, Университет Вандербильта, математический факультет. Как цитирует Пламмер (1993).
Кэмпбелл, SR; Эллингем, MN ; Ройл, Гордон Ф. (1993), «Характеристика хорошо покрытых кубических графов», Журнал комбинаторной математики и комбинаторных вычислений , 13 : 193–212, MR 1220613.
Кэмпбелл, Стивен Р.; Пламмер, Майкл Д. (1988), «О хорошо покрытых 3-многогранниках», Ars Combinatoria , 25 (A): 215–242, MR 0942505.
Каро, Яир; Себё, Андраш ; Тарси, Майкл (1996), «Распознавание жадных структур», Журнал алгоритмов , 20 (1): 137–156, doi : 10.1006/jagm.1996.0006, MR 1368720.
Chvátal, Václav ; Slater, Peter J. (1993), "Заметка о хорошо покрытых графах", Quo vadis, теория графов? , Annals of Discrete Mathematics, т. 55, Амстердам: Северная Голландия, стр. 179–181, MR 1217991.
Кук, Дэвид II; Нагель, Уве (2010), «Графы Коэна-Маколея и векторы граней комплексов флагов», SIAM Journal on Discrete Mathematics , 26 : 89–101, arXiv : 1003.4447 , Bibcode : 2010arXiv1003.4447C, doi : 10.1137/100818170.
Дохтерманн, Антон; Энгстрём, Александр (2009), «Алгебраические свойства идеалов ребер с помощью комбинаторной топологии», Electronic Journal of Combinatorics , 16 (2): Research Paper 2, doi : 10.37236/68 , MR 2515765.
Фаварон, О. (1982), «Очень хорошо покрытые графы», Дискретная математика , 42 (2–3): 177–187, doi : 10.1016/0012-365X(82)90215-1 , MR 0677051.
Финбоу, А.С.; Хартнелл, Б.Л. (1983), «Игра, связанная с покрытием звездами», Ars Combinatoria , 16 (A): 189–198, MR 0737090.
Финбоу, А.; Хартнелл, Б.; Новаковски, Р. (1988), «Хорошо доминируемые графы: коллекция хорошо покрытых графов», Ars Combinatoria , 25 (A): 5–10, MR 0942485.
Finbow, A.; Hartnell, B.; Nowakowski, RJ (1993), "Характеристика хорошо покрытых графов с обхватом 5 или больше", Журнал комбинаторной теории , Серия B, 57 (1): 44–68, doi : 10.1006/jctb.1993.1005 , MR 1198396.
Финбоу, А.; Хартнелл, Б.; Новаковски, Р.; Пламмер, Майкл Д. (2003), «О хорошо покрытых триангуляциях. I», Дискретная прикладная математика , 132 (1–3): 97–108, doi : 10.1016/S0166-218X(03)00393-7 , MR 2024267.
Финбоу, Артур С.; Хартнелл, Берт Л.; Новаковски, Ричард Дж.; Пламмер, Майкл Д. (2009), «О хорошо покрытых триангуляциях. II», Дискретная прикладная математика , 157 (13): 2799–2817, doi : 10.1016/j.dam.2009.03.014 , MR 2537505.
Финбоу, Артур С.; Хартнелл, Берт Л.; Новаковски, Ричард Дж.; Пламмер, Майкл Д. (2010), «О хорошо покрытых триангуляциях. III», Дискретная прикладная математика , 158 (8): 894–912, doi : 10.1016/j.dam.2009.08.002 , MR 2602814.
Финбоу, Артур С.; Хартнелл, Берт Л.; Новаковски, Ричард Дж.; Пламмер, Майкл Д. (2016), «Хорошо покрытые триангуляции: Часть IV», Дискретная прикладная математика , 215 : 71–94, doi : 10.1016/j.dam.2016.06.030 , MR 3548980.
Финк, Дж. Ф.; Якобсон, М. С.; Кинч, Л. Ф.; Робертс, Дж. (1985), «О графах, имеющих доминирующее число в два раза меньше их порядка», Period. Math. Hungar. , 16 (4): 287–293, doi :10.1007/BF01848079, MR 0833264, S2CID 121734811.
Гринберг, Питер (1993), «Кусочная геометрия $SL 2 Z »,$ Труды Американского математического общества , 335 (2): 705–720, doi :10.2307/2154401, JSTOR 2154401, MR 1140914.
Холройд, Фред; Талбот, Джон (2005), «Графы со свойством Эрдёша-Ко-Радо», Дискретная математика , 293 (1–3): 165–176, arXiv : math/0307073 , doi : 10.1016/j.disc.2004.08.028, MR 2136060.
Lesk, M.; Plummer, MD; Pulleyblank, WR (1984), «Эквивалентные графы», в Bollobás, Béla (ред.), Graph Theory and Combinatorics: Proceedings of the Cambridge Combinatoric Conference, in Honour of Paul Erdős , London: Academic Press, стр. 239–254, MR 0777180.
Пламмер, Майкл Д. (1970), «Некоторые концепции покрытия в графах», Журнал комбинаторной теории , 8 : 91–98, doi : 10.1016/S0021-9800(70)80011-4 , MR 0289347.
Пламмер, Майкл Д. (1993), «Хорошо покрытые графы: обзор», Quaestiones Mathematicae , 16 (3): 253–287, doi :10.1080/16073606.1993.9631737, MR 1254158, архивировано из оригинала 27 мая 2012 г..
Рагхаван, Виджай; Спинрад, Джереми (2003), «Надежные алгоритмы для ограниченных доменов», Журнал алгоритмов , 48 (1): 160–172, doi :10.1016/S0196-6774(03)00048-8, MR 2006100, S2CID 16327087.
Равиндра, Г. (1977), «Хорошо покрытые графы», Журнал комбинаторики, информационных и системных наук , 2 (1): 20–21, MR 0469831.
Санкаранараяна, Рамеш С. (1994), Хорошо покрытые графы: некоторые новые подклассы и результаты по сложности (докторская диссертация), Университет Альберты
Санкаранараяна, Рамеш С.; Стюарт, Лорна К. (1992), «Результаты сложности для хорошо покрытых графов», Networks , 22 (3): 247–262, CiteSeerX 10.1.1.47.9278 , doi :10.1002/net.3230220304, MR 1161178.
Стэплз, Дж. (1975), О некоторых подклассах хорошо покрытых графов , докторская диссертация, Университет Вандербильта, математический факультет. Как цитирует Пламмер (1993).
Самнер, Дэвид П. (1979), «Случайно сопоставляемые графы», Журнал теории графов , 3 (2): 183–186, doi :10.1002/jgt.3190030209, MR 0530304.
Танкус, Дэвид; Тарси, Майкл (1996), «Хорошо покрытые графы без клешней», Журнал комбинаторной теории , Серия B, 66 (2): 293–302, doi : 10.1006/jctb.1996.0022 , MR 1376052.
Танкус, Дэвид; Тарси, Майкл (1997), «Структура хорошо покрытых графов и сложность проблем их распознавания», Журнал комбинаторной теории , Серия B, 69 (2): 230–233, doi : 10.1006/jctb.1996.1742 , MR 1438624.