Центр удара

Центр удара — это точка на вытянутом массивном объекте, прикрепленном к шарниру, где перпендикулярный удар не вызовет реактивного удара на шарнире. Поступательные и вращательные движения отменяются на шарнире, когда импульсный удар наносится в центр удара. Центр удара часто обсуждается в контексте биты, ракетки , двери, меча или другого вытянутого объекта, удерживаемого за один конец.

Эта же точка называется центром колебаний для объекта, подвешенного к оси вращения в качестве маятника , то есть простой маятник, вся масса которого сосредоточена в этой точке, будет иметь тот же период колебаний, что и составной маятник.

В спорте центр удара битой, ракеткой или клюшкой связан с так называемой « зоной наилучшего восприятия », но последняя также связана с вибрационным изгибом объекта.

Объяснение

Эффект удара по подвешенной балке. ЦП — центр удара, ЦМ — центр масс балки.

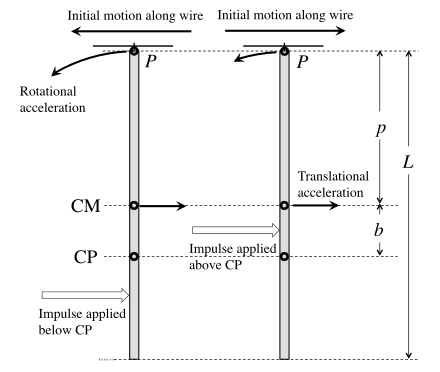
Представьте себе жесткую балку, подвешенную к проволоке с помощью приспособления, которое может свободно скользить по проволоке в точке P, как показано на рисунке. Импульсный удар наносится слева. Если он находится ниже центра масс (ЦМ), он заставит балку вращаться против часовой стрелки вокруг ЦМ, а также заставит ЦМ двигаться вправо. Центр удара (ЦП) находится ниже ЦМ. Если удар приходится выше ЦП, то правое поступательное движение будет больше, чем левое вращательное движение в точке P, в результате чего чистое начальное движение приспособления будет направлено вправо. Если удар приходится ниже ЦП, произойдет обратное, вращательное движение в точке P будет больше, чем поступательное движение, и приспособление первоначально будет двигаться влево. Только если удар приходится точно на ЦП, два компонента движения будут погашены, что даст нулевое чистое начальное движение в точке P.

При замене скользящего крепления на шарнир, который не может двигаться влево или вправо, импульсный удар в любом месте, кроме КП, приводит к возникновению первоначальной реактивной силы на шарнире.

Расчет центра удара

Общий случай

Для свободной жесткой балки импульс прикладывается под прямым углом в точке удара, определяемой как расстояние от центра масс (ЦМ). ${\displaystyle Fdt}$ ${\displaystyle b}$

Сила приводит к изменению скорости ЦМ, т.е .: ${\displaystyle dv_{cm}}$

${\displaystyle F=M{\frac {dv_{cm}}{dt}},}$

где - масса балки. ${\displaystyle M}$

Более того, сила создает крутящий момент вокруг ЦМ, что приводит к изменению угловой скорости балки, т.е .: ${\displaystyle \omega }$ ${\displaystyle d\omega }$

${\displaystyle Fb=I{\frac {d\omega }{dt}},}$

где - момент инерции относительно ЦМ. ${\displaystyle I}$

Для любой точки P, находящейся на расстоянии с противоположной стороны ЦМ от точки удара, изменение скорости точки P равно: ${\displaystyle p}$

${\displaystyle dv_{net}=dv_{cm}-pd\omega .}$

Следовательно, ускорение в точке P, вызванное импульсным ударом, равно:

${\displaystyle {\frac {dv_{net}}{dt}}=\left({\frac {1}{M}}-{\frac {pb}{I}}\right)F.}$

Центр удара (ЦП) — это точка, где это ускорение равно нулю (т.е. = 0), а сила не равна нулю (т.е. F ≠ 0). Таким образом, в центре удара условие имеет вид: ${\displaystyle {\tfrac {dv_{net}}{dt}}}$

${\displaystyle {\frac {1}{M}}-{\frac {pb}{I}}=0.}$

Следовательно, КП находится на расстоянии от ЦМ, определяемом формулой:

${\displaystyle b={\frac {I}{pM}}.}$

Обратите внимание, что ось вращения P не обязательно должна находиться на конце балки, а может быть выбрана на любом расстоянии . ${\displaystyle p}$

Длина также определяет центр колебаний физического маятника , то есть положение массы простого маятника, имеющего тот же период, что и физический маятник. ^[1] ${\displaystyle b+p}$

Центр удара однородного пучка

Для частного случая балки однородной плотности длиной момент инерции относительно ЦМ равен: ${\displaystyle L}$

${\displaystyle I={\frac {1}{12}}ML^{2}}$(см. момент инерции для вывода),

и для вращения вокруг оси на конце,

${\displaystyle p=L/2}$.

Это приводит к:

${\displaystyle b={\frac {L^{2}}{12p}}={\frac {1}{6}}L}$.

Отсюда следует, что CP составляет 2/3 длины однородной балки от поворотного конца. ${\displaystyle L}$

Некоторые приложения

Например, распашная дверь, которая останавливается дверным упором, размещенным на 2/3 ширины двери, выполнит свою работу с минимальным дрожанием двери, поскольку шарнирный конец не подвергается воздействию чистой реактивной силы. (Эта точка также является узлом во второй колебательной гармонике, что также минимизирует вибрацию.)

Сладкая точка на бейсбольной бите обычно определяется как точка, в которой удар ощущается лучше всего для отбивающего. Центр перкуссии определяет место, где, если бита ударяет по мячу, а руки отбивающего находятся в точке опоры, отбивающий не чувствует внезапной реактивной силы. Однако, поскольку бита не является жестким объектом, вибрации, производимые ударом, также играют свою роль. Кроме того, точка опоры замаха может не находиться в том месте, где находятся руки отбивающего. Исследования показали, что доминирующий физический механизм при определении того, где находится сладкая точка, возникает из расположения узлов в колебательных модах биты, а не из расположения центра перкуссии. ^[2]

Концепция центра удара может быть применена к мечам . Будучи гибкими объектами, «золотая середина» для такого режущего оружия зависит не только от центра удара, но и от характеристик изгиба и вибрации. ^{[3] [4]}

Ссылки

1. Рассел, Дэниел А. (16 июня 2005 г.). «Что такое COP и имеет ли это значение?». Физика и акустика бейсбольных и софтбольных бит . Университет штата Пенсильвания . Архивировано из оригинала 5 апреля 2009 г. Получено 24 мая 2012 г.
2. Кросс, Род (2004). «Центр ударных действий ручных инструментов» (PDF) . Американский журнал физики . 72 (5): 622–630. Bibcode :2004AmJPh..72..622C. doi :10.1119/1.1634965.
3. Тернер, Джордж (1999). «Движения и удары мечом: исследование и анализ». Ассоциация боевых искусств эпохи Возрождения . Получено 24 мая 2012 г.
4. Гайслер, Роберт (2014). «О динамике мечей». HROARR. Архивировано из оригинала 2021-03-05 . Получено 30 марта 2021 г.