Уравнения Лотки–Вольтерра

Уравнения, моделирующие циклы хищник–жертва

Уравнения Лотки–Вольтерры , также известные как модель хищник–жертва Лотки–Вольтерры , представляют собой пару нелинейных дифференциальных уравнений первого порядка , часто используемых для описания динамики биологических систем , в которых взаимодействуют два вида, один как хищник , а другой как добыча. Популяции изменяются со временем в соответствии с парой уравнений: $${\displaystyle {\begin{aligned}{\frac {dx}{dt}}&=\alpha x-\beta xy,\\{\frac {dy}{dt}}&=-\gamma y+\delta xy,\end{aligned}}}$$

где

• переменная x — плотность популяции добычи ( например, количество кроликов на квадратный километр);
• переменная y — плотность популяции некоторого хищника (например, количество лис на квадратный километр);
• ${\displaystyle {\tfrac {dy}{dt}}}$и представляют собой мгновенные темпы роста двух популяций; ${\displaystyle {\tfrac {dx}{dt}}}$
• t представляет время;
• Параметры добычи α и β описывают, соответственно, максимальную скорость роста добычи на душу населения и влияние присутствия хищников на уровень смертности добычи.
• Параметры хищника γ и δ описывают соответственно уровень смертности хищника на душу населения и влияние присутствия добычи на скорость роста хищника.
• Все параметры положительны и реальны.

Решение дифференциальных уравнений является детерминированным и непрерывным . Это, в свою очередь, подразумевает, что поколения как хищника, так и жертвы постоянно перекрываются. ^[1]

Система уравнений Лотки–Вольтерры является примером популяционной модели Колмогорова (не путать с более известными уравнениями Колмогорова ) ^{[2] [3] [4]} , которая представляет собой более общую структуру, позволяющую моделировать динамику экологических систем с взаимодействиями хищник–жертва, конкуренцией , болезнями и мутуализмом .

Биологическая интерпретация и предположения модели

Предполагается, что добыча имеет неограниченный запас пищи и размножается экспоненциально, если только не подвергается хищничеству; этот экспоненциальный рост представлен в уравнении выше членом αx . Предполагается, что скорость хищничества добычи пропорциональна скорости, с которой встречаются хищники и добыча; это представлено выше членом βxy . Если x или y равны нулю, то хищничества быть не может. С этими двумя членами уравнение добычи выше можно интерпретировать следующим образом: скорость изменения популяции добычи определяется ее собственной скоростью роста за вычетом скорости, с которой на нее охотятся.

Член δxy представляет рост популяции хищников. (Обратите внимание на сходство со скоростью хищничества; однако используется другая константа, поскольку скорость, с которой растет популяция хищников, не обязательно равна скорости, с которой он потребляет добычу). Член γy представляет скорость потери хищников из-за естественной смерти или эмиграции; это приводит к экспоненциальному спаду при отсутствии добычи. Следовательно, уравнение выражает, что скорость изменения популяции хищника зависит от скорости, с которой он потребляет добычу, за вычетом его собственной скорости смертности.

Модель хищник-жертва Лотки-Вольтерры делает ряд предположений относительно окружающей среды и биологии популяций хищников и жертв: ^[5]

1. Популяция добычи всегда находит достаточно пищи.
2. Обеспеченность популяции хищников пищей полностью зависит от численности популяции жертв.
3. Скорость изменения численности населения пропорциональна его численности.
4. В ходе этого процесса окружающая среда не меняется в пользу одного вида, а генетическая адаптация не имеет значения.
5. Хищники обладают безграничным аппетитом.
6. Обе популяции можно описать одной переменной. Это равносильно предположению, что популяции не имеют пространственного или возрастного распределения, которое вносит вклад в динамику.

Биологическая значимость модели

Количество шкурок зайца-беляка (желтый, фон) и канадской рыси (черная линия, передний план), проданных компании Hudson's Bay Company . Канадские рыси едят зайцев-беляков.

Ни одно из вышеприведенных предположений, вероятно, не будет справедливым для естественных популяций. Тем не менее, модель Лотки–Вольтерры показывает два важных свойства популяций хищников и жертв, и эти свойства часто распространяются на варианты модели, в которых эти предположения смягчены:

Во-первых, динамика популяций хищников и жертв имеет тенденцию к колебаниям. Колебания численности хищников и жертв наблюдались в естественных популяциях, таких как данные по рысям и зайцам-белякам компании Hudson's Bay Company ^[6] и популяции лосей и волков в национальном парке Isle Royale . ^[7]

Во-вторых, равновесие популяции этой модели обладает тем свойством, что равновесная плотность добычи (задается как ) зависит от параметров хищника, а равновесная плотность хищника (задается как ) от параметров жертвы. Это имеет следствием то, что увеличение, например, скорости роста добычи, , приводит к увеличению равновесной плотности хищника, но не равновесной плотности добычи. Улучшение среды обитания для добычи приносит пользу хищнику, а не добыче (это связано с парадоксом пестицидов и парадоксом обогащения ). Демонстрацией этого явления является увеличение процента вылавливаемых хищных рыб в годы Первой мировой войны (1914–18), когда скорость роста добычи увеличилась из-за сокращения рыболовного усилия. ${\displaystyle x=\gamma /\delta }$ ${\displaystyle y=\alpha /\beta }$ ${\displaystyle \alpha }$

Еще одним примером является экспериментальное удобрение океана железом. В нескольких экспериментах в океане растворялось большое количество солей железа. Ожидалось, что железо, которое является ограничивающим питательным веществом для фитопланктона, будет стимулировать рост фитопланктона и что оно будет поглощать углекислый газ из атмосферы. Добавление железа обычно приводит к кратковременному цветению фитопланктона, который быстро потребляется другими организмами (такими как мелкая рыба или зоопланктон ) и ограничивает эффект обогащения в основном увеличением плотности хищников, что, в свою очередь, ограничивает поглощение углерода. Это предсказывается равновесными плотностями популяции модели хищник-жертва Лотки-Вольтерры и является особенностью, которая переносится на более сложные модели, в которых ограничивающие предположения простой модели смягчены. ^[8]

Приложения к экономике и маркетингу

Модель Лотки–Вольтерры имеет дополнительные приложения в таких областях, как экономика ^[9] и маркетинг. ^{[10] [11]} Ее можно использовать для описания динамики на рынке с несколькими конкурентами, взаимодополняющими платформами и продуктами, экономикой совместного потребления и т. д. Существуют ситуации, в которых один из конкурентов вытесняет других конкурентов с рынка, и другие ситуации, в которых рынок достигает равновесия, где каждая фирма стабилизируется на своей доле рынка. Также можно описать ситуации, в которых происходят циклические изменения в отрасли или хаотические ситуации без равновесия, а изменения происходят часто и непредсказуемо.

История

Модель хищник–жертва Лотки–Вольтерры была первоначально предложена Альфредом Дж. Лотка в теории автокаталитических химических реакций в 1910 году. ^{[12] [13]} Это было фактически логистическое уравнение , ^[14] первоначально выведенное Пьером Франсуа Ферхюльстом . ^[15] В 1920 году Лотка расширил модель с помощью Андрея Колмогорова на «органические системы», используя в качестве примера вид растений и вид травоядных животных ^[16] , а в 1925 году он использовал уравнения для анализа взаимодействий хищник–жертва в своей книге по биоматематике . ^[17] Тот же набор уравнений был опубликован в 1926 году Вито Вольтеррой , математиком и физиком, который заинтересовался математической биологией . ^{[13] [18] [19]} Исследование Вольтерры было вдохновлено его взаимодействием с морским биологом Умберто Д'Анкона , который в то время ухаживал за его дочерью, а позже стал его зятем. Д'Анкона изучал уловы рыбы в Адриатическом море и заметил, что процент пойманной хищной рыбы увеличился в годы Первой мировой войны (1914–18). Это озадачило его, так как промысловое усилие было очень сильно сокращено в военные годы, и, поскольку предпочтительнее была добыча рыбы, можно было бы интуитивно ожидать, что это увеличит процент добычи рыбы. Вольтерра разработал свою модель, чтобы объяснить наблюдение Д'Анконы, и сделал это независимо от Альфреда Лотки. Он действительно отдал должное более ранней работе Лотки в своей публикации, после чего модель стала известна как «модель Лотки-Вольтерры». ^[20]

Позднее модель была расширена, включив в нее рост добычи, зависящий от плотности, и функциональную реакцию в форме, разработанной К. С. Холлингом ; модель, которая стала известна как модель Розенцвейга–МакАртура. ^[21] Обе модели, Лотки–Вольтерры и Розенцвейга–МакАртура, использовались для объяснения динамики естественных популяций хищников и добычи.

В конце 1980-х годов появилась альтернатива модели хищник-жертва Лотки-Вольтерры (и ее обобщениям, зависящим от общей жертвы), модель, зависящая от отношения, или модель Ардити-Гинзбурга . ^[22] Обоснованность моделей, зависящих от отношения или добычи, была предметом многочисленных споров. ^[23]

Уравнения Лотки–Вольтерры имеют долгую историю использования в экономической теории ; их первоначальное применение обычно приписывают Ричарду Гудвину в 1965 ^[24] или 1967 годах. ^{[25] [26]}

Решения уравнений

Уравнения имеют периодические решения. Эти решения не имеют простого выражения в терминах обычных тригонометрических функций , хотя они вполне поддаются обработке. ^{[27] [28] [29]}

Если ни один из неотрицательных параметров α , β , γ , δ не обращается в нуль, три из них можно поглотить в нормализацию переменных, оставив только один параметр: поскольку первое уравнение однородно по x , а второе — по y , параметры β / α и δ / γ поглощаются в нормализациях y и x соответственно, а γ — в нормализацию t , так что произвольным остается только α / γ . Это единственный параметр, влияющий на характер решений.

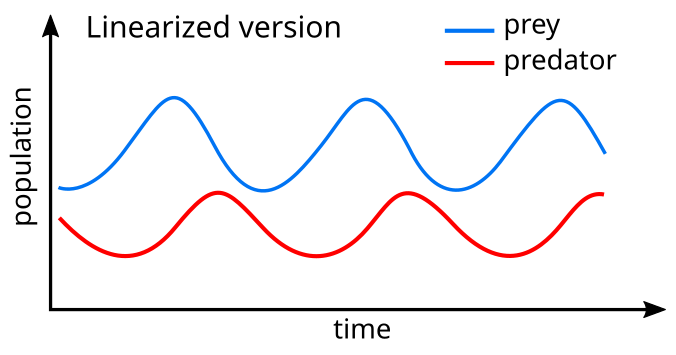
Линеаризация уравнений дает решение, похожее на простое гармоническое движение ^[30], при этом популяция хищников отстает от популяции жертв на 90° в цикле.

Простой пример

Динамика популяции кроликов и лисиц была упомянута отдельно.

Фазовый график для задачи «хищник-жертва» для различных начальных условий популяции хищников.

Предположим, что есть два вида животных: кролик (добыча) и лиса (хищник). Если начальная плотность составляет 10 кроликов и 10 лис на квадратный километр, можно построить график изменения численности двух видов с течением времени; при условии, что показатели роста и смертности кроликов составляют 1,1 и 0,4, а лис — 0,1 и 0,4 соответственно. Выбор временного интервала произволен.

Можно также параметрически построить решения в виде орбит в фазовом пространстве , не отображая время, но с одной осью, представляющей количество добычи, а другой осью, представляющей плотность хищников для всех моментов времени.

Это соответствует исключению времени из двух дифференциальных уравнений выше для получения одного дифференциального уравнения

${\displaystyle {\frac {dy}{dx}}=-{\frac {y}{x}}{\frac {\delta x-\gamma }{\beta y-\alpha }}}$

связывая переменные x (хищник) и y (жертва). Решения этого уравнения — замкнутые кривые. Оно поддается разделению переменных : интегрирование

${\displaystyle {\frac {\beta y-\alpha }{y}}\,dy+{\frac {\delta x-\gamma }{x}}\,dx=0}$

дает неявную связь

${\displaystyle V=\delta x-\gamma \ln(x)+\beta y-\alpha \ln(y),}$

где V — постоянная величина, зависящая от начальных условий и сохраняющаяся на каждой кривой.

Примечание: Эти графики иллюстрируют серьезное потенциальное ограничение в применении в качестве биологической модели: для этого конкретного выбора параметров в каждом цикле популяция кроликов сокращается до крайне низких значений, но восстанавливается (в то время как популяция лис остается значительной при самой низкой плотности кроликов). Однако в реальных ситуациях случайные колебания дискретного числа особей могут привести к фактическому вымиранию кроликов, а следовательно, и лис. Эта проблема моделирования была названа «проблемой атто-лисы», атто - лиса представляет собой условные 10−18 ^лисы . ^{[31] [32]} Плотность 10−18 ^лис на квадратный километр соответствует в среднем приблизительно 5×10−10 ^лис на поверхности Земли, что на практике означает, что лисы вымерли.

Гамильтонова структура системы

Поскольку величина сохраняется с течением времени, она играет роль функции Гамильтона системы. ^[33] Чтобы увидеть это, мы можем определить скобку Пуассона следующим образом . Тогда уравнения Гамильтона будут иметь вид Переменные и не являются каноническими, так как . Однако, используя преобразования ^[34] , мы пришли к канонической форме уравнений Гамильтона, включающей гамильтониан : Скобка Пуассона для канонических переменных теперь принимает стандартный вид . ${\displaystyle V(x,y)}$ ${\displaystyle \{f(x,y),g(x,y)\}=-xy\left({\frac {\partial f}{\partial x}}{\frac {\partial g}{\partial y}}-{\frac {\partial f}{\partial y}}{\frac {\partial g}{\partial x}}\right)}$ $${\displaystyle {\begin{cases}{\dot {x}}=\{x,V\}=\alpha x-\beta xy,\\{\dot {y}}=\{y,V\}=\delta xy-\gamma y.\end{cases}}}$$ ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle \{x,y\}=-xy\neq 1}$ ${\displaystyle p=\ln(x)}$ ${\displaystyle q=\ln(y)}$ ${\displaystyle H(q,p)=V(x(q,p),y(q,p))=\delta e^{p}-\gamma p+\beta e^{q}-\alpha q}$ $${\displaystyle {\begin{cases}{\dot {q}}={\frac {\partial H}{\partial p}}=\delta e^{p}-\gamma ,\\{\dot {p}}=-{\frac {\partial H}{\partial q}}=\alpha -\beta e^{q}.\end{cases}}}$$ ${\displaystyle (q,p)}$ ${\displaystyle \{F(q,p),G(q,p)\}=\left({\frac {\partial F}{\partial q}}{\frac {\partial G}{\partial p}}-{\frac {\partial F}{\partial p}}{\frac {\partial G}{\partial q}}\right)}$

Фазовый график еще одного примера

Менее экстремальный пример:

α = 2/3 , β = 4/3 , γ = 1 = δ . Предположим, что x , y количественно измеряют тысячи каждый. Круги представляют начальные условия добычи и хищника от x = y = 0,9 до 1,8 с шагом 0,1. Фиксированная точка находится в точке (1, 1/2).

Динамика системы

В модельной системе хищники процветают, когда добыча в изобилии, но в конечном итоге превосходят свои запасы пищи и приходят в упадок. Когда популяция хищников низкая, популяция добычи снова увеличится. Эта динамика продолжается в цикле роста и упадка популяции .

Равновесие населения

Равновесие численности населения в модели достигается, когда ни один из уровней численности населения не изменяется, т.е. когда обе производные равны 0: $${\displaystyle x(\alpha -\beta y)=0,}$$ $${\displaystyle -y(\gamma -\delta x)=0.}$$

Приведенная выше система уравнений дает два решения: и $${\displaystyle \{y=0,\ \ x=0\}}$$ $${\displaystyle \left\{y={\frac {\alpha }{\beta }},\ \ x={\frac {\gamma }{\delta }}\right\}.}$$

Следовательно, существует два равновесия.

Первое решение фактически представляет вымирание обоих видов. Если обе популяции равны 0, то они будут оставаться такими неопределенно долго. Второе решение представляет фиксированную точку, в которой обе популяции поддерживают свои текущие, ненулевые численности, и, в упрощенной модели, делают это неопределенно долго. Уровни популяции, при которых достигается это равновесие, зависят от выбранных значений параметров α , β , γ и δ .

Устойчивость неподвижных точек

Устойчивость неподвижной точки в начале координат можно определить, выполнив линеаризацию с использованием частных производных .

Матрица Якоби модели «хищник-жертва» известна как матрица сообщества . $${\displaystyle J(x,y)={\begin{bmatrix}\alpha -\beta y&-\beta x\\\delta y&\delta x-\gamma \end{bmatrix}}.}$$

Первая фиксированная точка (вымирание)

При оценке в устойчивом состоянии (0, 0) матрица Якоби J становится $${\displaystyle J(0,0)={\begin{bmatrix}\alpha &0\\0&-\gamma \end{bmatrix}}.}$$

Собственные значения этой матрицы равны $${\displaystyle \lambda _{1}=\alpha ,\quad \lambda _{2}=-\gamma .}$$

В модели α и γ всегда больше нуля, и, таким образом, знак собственных значений выше всегда будет отличаться. Следовательно, неподвижная точка в начале координат является седловой точкой .

Нестабильность этой фиксированной точки имеет значение. Если бы она была стабильной, ненулевые популяции могли бы притягиваться к ней, и, как таковая, динамика системы могла бы привести к вымиранию обоих видов для многих случаев начальных уровней популяции. Однако, поскольку фиксированная точка в начале координат является седловой точкой и, следовательно, нестабильна, из этого следует, что вымирание обоих видов в модели затруднено. (На самом деле, это могло бы произойти только в том случае, если бы добыча была полностью уничтожена искусственно, в результате чего хищники умерли бы от голода. Если бы хищники были уничтожены, популяция добычи неограниченно росла бы в этой простой модели.) Популяции добычи и хищника могут приближаться к нулю на бесконечно малую величину и все равно восстанавливаться.

Вторая неподвижная точка (колебания)

Оценка J во второй фиксированной точке приводит к $${\displaystyle J\left({\frac {\gamma }{\delta }},{\frac {\alpha }{\beta }}\right)={\begin{bmatrix}0&-{\frac {\beta \gamma }{\delta }}\\{\frac {\alpha \delta }{\beta }}&0\end{bmatrix}}.}$$

Собственные значения этой матрицы равны $${\displaystyle \lambda _{1}=i{\sqrt {\alpha \gamma }},\quad \lambda _{2}=-i{\sqrt {\alpha \gamma }}.}$$

Поскольку собственные значения являются чисто мнимыми и сопряженными друг с другом, эта неподвижная точка должна быть либо центром для замкнутых орбит в локальной окрестности, либо притягивающей или отталкивающей спиралью. В консервативных системах должны быть замкнутые орбиты в локальной окрестности неподвижных точек, которые существуют в минимумах и максимумах сохраняющейся величины. Сохраняющаяся величина выведена выше как находящаяся на орбитах. Таким образом, орбиты вокруг неподвижной точки являются замкнутыми и эллиптическими , поэтому решения являются периодическими, колеблющимися на малом эллипсе вокруг неподвижной точки с частотой и периодом . ${\displaystyle V=\delta x-\gamma \ln(x)+\beta y-\alpha \ln(y)}$ ${\displaystyle \omega ={\sqrt {\lambda _{1}\lambda _{2}}}={\sqrt {\alpha \gamma }}}$ ${\displaystyle T=2{\pi }/({\sqrt {\lambda _{1}\lambda _{2}}})}$

Как показано на циркуляционных колебаниях на рисунке выше, кривые уровня представляют собой замкнутые орбиты, окружающие фиксированную точку: уровни популяций хищников и жертв циклически и колеблются без затухания вокруг фиксированной точки с частотой . ${\displaystyle \omega ={\sqrt {\alpha \gamma }}}$

Значение постоянной движения V , или, что то же самое, K = exp(− V ) , можно найти для замкнутых орбит вблизи неподвижной точки. ${\displaystyle K=y^{\alpha }e^{-\beta y}x^{\gamma }e^{-\delta x}}$

Увеличение K приближает замкнутую орбиту к неподвижной точке. Наибольшее значение константы K получается путем решения задачи оптимизации. Максимальное значение K при этом достигается в стационарной (неподвижной) точке и составляет где e — число Эйлера . $${\displaystyle y^{\alpha }e^{-\beta y}x^{\gamma }e^{-\delta x}={\frac {y^{\alpha }x^{\gamma }}{e^{\delta x+\beta y}}}\longrightarrow \max _{x,y>0}.}$$ ${\displaystyle \left({\frac {\gamma }{\delta }},{\frac {\alpha }{\beta }}\right)}$ $${\displaystyle K^{*}=\left({\frac {\alpha }{\beta e}}\right)^{\alpha }\left({\frac {\gamma }{\delta e}}\right)^{\gamma },}$$

Смотрите также

• Конкурентные уравнения Лотки–Вольтерры
• Обобщенное уравнение Лотки–Вольтерра
• Мутуализм и уравнение Лотки–Вольтерры
• Матрица сообщества
• Динамика численности населения
• Динамика численности рыбных хозяйств
• Модель Николсона–Бейли
• Система реакция-диффузия
• Парадокс обогащения
• Законы Ланчестера , аналогичная система дифференциальных уравнений для военных сил
• Случайная обобщенная модель Лотки–Вольтерры
• Модель «потребитель-ресурс»

Примечания

1. Кук, Д.; Хиорнс, Р. В.; и др. (1981). Математическая теория динамики биологических популяций . Том II. Academic Press.
2. Фридман, HI (1980). Детерминированные математические модели в популяционной экологии . Марсель Деккер .
3. Брауэр, Ф.; Кастильо-Чавес, К. (2000). Математические модели в популяционной биологии и эпидемиологии . Springer-Verlag .
4. Хоппенстедт, Ф. (2006). "Модель хищник-жертва". Scholarpedia . 1 (10): 1563. Bibcode :2006SchpJ...1.1563H. doi : 10.4249/scholarpedia.1563 .
5. "ДИНАМИКА ХИЩНИКА-ДОБЫЧИ". www.tiem.utk.edu . Архивировано из оригинала 2012-12-15 . Получено 2018-01-09 .
6. Гилпин, М. Э. (1973). «Едят ли зайцы рысей?». American Naturalist . 107 (957): 727–730. doi :10.1086/282870. S2CID  84794121.
7. Jost, C.; Devulder, G.; Vucetich, JA; Peterson, R.; Arditi, R. (2005). «Волки острова Айл-Ройал демонстрируют масштабно-инвариантное насыщение и зависящее от плотности хищничество по отношению к лосям». J. Anim. Ecol . 74 (5): 809–816. doi :10.1111/j.1365-2656.2005.00977.x.
8. Pan, A.; Pourziaei, B.; Huang, H. (2015-06-03). «Влияние удобрения океана железом на биологический углеродный насос фитопланктона». Успехи в прикладной математике и механике . 3 (1): 52–64. doi :10.4208/aamm.10-m1023. S2CID  124606355.
9. Прасолов, Александр В. (2016). Некоторые количественные методы и модели в экономической теории . Экономические вопросы, проблемы и перспективы. Нью-Йорк: Nova Publishers. ISBN 978-1-63484-937-1.
10. Hung, Hui-Chih; Chiu, Yu-Chih; Wu, Muh-Cherng (2017). «Модифицированная модель Лотки–Вольтерры для диффузии и замены многопоколенческих технологий обработки DRAM». Математические проблемы в машиностроении . 2017 : 1–12. doi : 10.1155/2017/3038203 . ISSN  1024-123X.
11. Орбах, Яир (2022). Прогнозирование динамики рынка и технологий . Израиль: Ariel University Press. С. 123–143. ISBN 978-965-7632-40-6.
12. Лотка, А. Дж. (1910). «Вклад в теорию периодической реакции». J. Phys. Chem. 14 (3): 271–274. doi :10.1021/j150111a004.
13. Goel, NS; et al. (1971). О моделях Вольтерра и других нелинейных моделях взаимодействующих популяций . Academic Press. ISBN 0-12-287450-1.
14. Берриман, А.А. (1992). «Истоки и эволюция теории хищник-жертва» (PDF) . Экология . 73 (5): 1530–1535. doi :10.2307/1940005. JSTOR  1940005. Архивировано из оригинала (PDF) 2010-05-31.
15. Верхюльст, PH (1838). «Обратите внимание на то, что население стремится к росту сына». Корр. Математика и физика . 10 : 113–121.
16. Лотка, А. Дж. (1920). «Аналитическая заметка о некоторых ритмических отношениях в органических системах». Proc. Natl. Acad. Sci. USA 6 (7): 410–415. Bibcode :1920PNAS....6..410L. doi : 10.1073/pnas.6.7.410 . PMC 1084562 . PMID  16576509.  
17. Лотка, А. Дж. (1925). Элементы физической биологии . Уильямс и Уилкинс .
18. Вольтерра, В. (1926). «Вариации и колебания количества людей в приятных видах животных». Память акад. Линчей Рома . 2 : 31–113.
19. Вольтерра, В. (1931). «Изменения и колебания числа особей у видов животных, живущих вместе». В Chapman, RN (ред.). Экология животных . McGraw–Hill .
20. Кингсленд, С. (1995). Моделирование природы: эпизоды в истории популяционной экологии . Издательство Чикагского университета. ISBN 978-0-226-43728-6.
21. Розенцвейг, ML; Макартур, RH (1963). «Графическое представление и условия стабильности взаимодействий хищник-жертва». American Naturalist . 97 (895): 209–223. doi :10.1086/282272. S2CID  84883526.
22. Arditi, R.; Ginzburg, LR (1989). "Coupling in predator-prey dynamics: ratio dependency" (PDF) . Journal of Theoretical Biology . 139 (3): 311–326. Bibcode :1989JThBi.139..311A. doi :10.1016/s0022-5193(89)80211-5. Архивировано из оригинала (PDF) 2016-03-04 . Получено 2013-06-26 .
23. Абрамс, ПА; Гинзбург, ЛР (2000). «Природа хищничества: зависимость от добычи, зависимость от соотношения или ни то, ни другое?». Тенденции в экологии и эволюции . 15 (8): 337–341. doi :10.1016/s0169-5347(00)01908-x. PMID  10884706.
24. Гандольфо, Г. (2008). «Джузеппе Паломба и уравнения Лотки – Вольтерра». Рендиконти Линчеи . 19 (4): 347–357. дои : 10.1007/s12210-008-0023-7. S2CID  140537163.
25. Гудвин, Р. М. (1967). "Цикл роста" . В Feinstein, CH (ред.). Социализм, капитализм и экономический рост . Cambridge University Press .
26. Desai, M.; Ormerod, P. (1998). "Richard Goodwin: A Short Appreciation" (PDF) . The Economic Journal . 108 (450): 1431–1435. CiteSeerX 10.1.1.423.1705 . doi :10.1111/1468-0297.00350. Архивировано из оригинала (PDF) 27-09-2011 . Получено 22-03-2010 . 
27. Штайнер, Антонио; Гандер, Мартин Якоб (1999). «Parametrische Lösungen der Räuber-Beute-Gleichungen im Vergleich». Иль Вольтерриано . 7 : 32–44.
28. Эванс, CM; Финдли, GL (1999). «Новое преобразование для проблемы Лотки-Вольтерры». Журнал математической химии . 25 : 105–110. doi :10.1023/A:1019172114300. S2CID  36980176.
29. Leconte, M.; Masson, P.; Qi, L. (2022). «Осцилляции предельного цикла, время отклика и зависящее от времени решение модели хищник-жертва Лотки-Вольтерры». Physics of Plasmas . 29 (2): 022302. arXiv : 2110.11557 . doi :10.1063/5.0076085. S2CID  239616189.
30. Тонг, Х. (1983). Пороговые модели в нелинейном анализе временных рядов . Springer–Verlag.
31. Лобри, Клод; Сари, Тевфик (2015). «Миграции в модели Розенцвейга-МакАртура и проблема «атто-лисы»» (PDF) . Arima . 20 : 95–125.
32. Моллисон, Д. (1991). "Зависимость эпидемических и популяционных скоростей от основных параметров" (PDF) . Math. Biosci . 107 (2): 255–287. doi :10.1016/0025-5564(91)90009-8. PMID  1806118.
33. Nutku, I. (1990). "Гамильтонова структура уравнений Лотки-Вольтерры". Physics Letters A. 145 ( 1): 27–28. Bibcode :1990PhLA..145...27N. doi :10.1016/0375-9601(90)90270-X. hdl : 11693/26204 . S2CID  121710034.
34. Бейджент, Стив (2010-03-02). «Динамика Лотки-Вольтерры — введение» (PDF) .

Дальнейшее чтение

• Хофбауэр, Йозеф; Зигмунд, Карл (1998). «Динамические системы и уравнения Лотки–Вольтерры». Эволюционные игры и динамика популяций . Нью-Йорк: Cambridge University Press. С. 1–54. ISBN 0-521-62570-X.
• Каплан, Дэниел; Гласс, Леон (1995). Понимание нелинейной динамики . Нью-Йорк: Springer. ISBN 978-0-387-94440-1.
• Ли, Э. Р. (1968). «Экологическая роль уравнений Вольтерра». Некоторые математические проблемы в биологии .– современное обсуждение с использованием данных Компании Гудзонова залива о рысях и зайцах в Канаде с 1847 по 1903 год.
• Мюррей, Дж. Д. (2003). Математическая биология I: Введение . Нью-Йорк: Springer. ISBN 978-0-387-95223-9.'
• Конспект лекций Стефано Аллесины по курсу «Экология сообщества»: https://stefanoallesina.github.io/Theoretical_Community_Ecology/

Внешние ссылки

• Из проекта Wolfram Demonstrations Project — требуется проигрыватель CDF (бесплатно):
  • Уравнения «хищник–жертва»
  • Модель «хищник–жертва»
  • Динамика отношений «хищник–жертва» с функциональным ответом второго типа
  • Экосистема «хищник–жертва»: моделирование на основе агентов в реальном времени
• Алгоритмическое моделирование Лотки-Вольтерры (веб-симуляция).