3D-реконструкция из нескольких изображений

Создание 3D модели из набора изображений

3D-селфи в масштабе 1:20, напечатанное Shapeways с помощью гипсовой печати, создано парком миниатюр Мадуродам из 2D-фотографий, сделанных в фотобудке Fantasitron.

3D-модели создаются на основе 2D-фотографий, сделанных в фотобудке Fantasitron 3D в Мадюродаме .

Создание и реконструкция 3D-фигур из одно- или многоракурсных карт глубины или силуэтов ^[1]

3D-реконструкция из нескольких изображений — это создание трехмерных моделей из набора изображений. Это обратный процесс получения 2D-изображений из 3D-сцен.

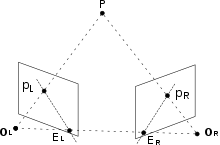
Суть изображения — это проекция с 3D-сцены на 2D-плоскость, в ходе которой глубина теряется. 3D-точка, соответствующая определенной точке изображения, ограничена тем, чтобы находиться на линии визирования. Из одного изображения невозможно определить, какая точка на этой линии соответствует точке изображения. Если доступны два изображения, то положение 3D-точки можно найти как пересечение двух проекционных лучей. Этот процесс называется триангуляцией . Ключом к этому процессу являются отношения между несколькими видами, которые передают информацию о том, что соответствующие наборы точек должны содержать некоторую структуру и что эта структура связана с позами и калибровкой камеры.

В последние десятилетия наблюдается значительный спрос на 3D-контент для компьютерной графики , виртуальной реальности и коммуникации, что приводит к изменению акцентов в требованиях. Многие существующие системы для построения 3D-моделей построены на основе специализированного оборудования (например, стереоустановок), что приводит к высокой стоимости, которая не может удовлетворить требования его новых приложений. Этот разрыв стимулирует использование цифровых средств обработки изображений (например, камеры). Ранний метод был предложен Томази и Канаде. ^[2] Они использовали подход аффинной факторизации для извлечения 3D из последовательностей изображений. Однако предположение об ортогональной проекции является существенным ограничением этой системы.

Обработка

Визуальный облик объекта можно восстановить из нескольких силуэтов. ^[3]

Задача преобразования нескольких 2D-изображений в 3D-модель состоит из ряда этапов обработки:

Калибровка камеры состоит из внутренних и внешних параметров, без которых на определенном уровне не может работать ни одна схема алгоритмов. Пунктирная линия между Калибровкой и Определением глубины показывает, что калибровка камеры обычно требуется для определения глубины.

Определение глубины является наиболее сложной частью всего процесса, поскольку оно вычисляет 3D-компонент, отсутствующий в любом данном изображении – глубину. Проблема соответствия , нахождение соответствий между двумя изображениями, чтобы положение сопоставленных элементов затем можно было триангулировать в 3D-пространстве, является здесь ключевой проблемой.

После того, как у вас есть несколько карт глубины, вам нужно объединить их, чтобы создать окончательную сетку, вычислив глубину и проецируя из камеры – регистрация . Калибровка камеры будет использоваться для определения того, где многочисленные сетки, созданные картами глубины, могут быть объединены для разработки более крупной, предоставляющей более одного вида для наблюдения.

На этапе применения материалов у вас есть полная 3D-сетка, что может быть конечной целью, но обычно вы захотите применить к сетке цвет из исходных фотографий. Это может варьироваться от случайного проецирования изображений на сетку, через подходы комбинирования текстур для сверхразрешения и, наконец, до сегментации сетки по материалу, например, по зеркальным и диффузным свойствам.

Математическое описание реконструкции

Дана группа 3D-точек, просматриваемых N камерами с матрицами , определить как однородные координаты проекции точки на камеру. Задача реконструкции может быть изменена на: дана группа пиксельных координат , найти соответствующий набор матриц камеры и структуру сцены, такую ​​что ${\displaystyle \{P^{i}\}_{i=1\ldots N}}$ ${\displaystyle m_{j}^{i}\simeq P^{i}w_{j}}$ ${\displaystyle j^{th}}$ ${\displaystyle i^{th}}$ ${\displaystyle \{m_{j}^{i}\}}$ ${\displaystyle \{P^{i}\}}$ ${\displaystyle \{w_{j}\}}$

${\displaystyle m_{j}^{i}\simeq P^{i}w_{j}}$(1)

В общем случае, без дополнительных ограничений, мы получим проективную реконструкцию. ^{[4] [5]} Если и удовлетворяют (1), то и будут удовлетворять (1) с любой невырожденной матрицей T размером 4 × 4 . ${\displaystyle \{P^{i}\}}$ ${\displaystyle \{w_{j}\}}$ ${\displaystyle \{P^{i}T\}}$ ${\displaystyle \{T^{-1}w_{j}\}}$

Проективную реконструкцию можно рассчитать только по соответствию точек без какой-либо априорной информации.

Автокалибровка

При автокалибровке или самокалибровке сначала восстанавливаются движение и параметры камеры с использованием жесткости. Затем можно легко рассчитать структуру. Два метода, реализующие эту идею, представлены ниже:

Уравнения Круппы

При минимум трех смещениях мы можем получить внутренние параметры камеры, используя систему полиномиальных уравнений Круппы ^[6], которые выводятся из геометрической интерпретации ограничения жесткости. ^{[7] [8]}

Матрица неизвестна в уравнениях Круппы, называется матрицей коэффициентов Круппы. С помощью K и методом факторизации Холецкого можно легко получить внутренние параметры: ${\displaystyle K=AA^{\top }}$

${\displaystyle K={\begin{bmatrix}k_{1}&k_{2}&k_{3}\\k_{2}&k_{4}&k_{5}\\k_{3}&k_{5}&1\\\end{bmatrix}}}$

Недавно Хартли ^[9] предложил более простую форму. Пусть будет записано как , где ${\displaystyle F}$ ${\displaystyle F=DUV^{\top }}$

Затем уравнения Круппы переписываются (вывод можно найти в ^[9] )

Мендонса и Чиполла

Этот метод основан на использовании ограничения жесткости. Разработать функцию стоимости, которая рассматривает внутренние параметры как аргументы, а фундаментальные матрицы как параметры. определяется как фундаментальная матрица, а как матрицы внутренних параметров. ${\displaystyle {F}_{ij}}$ ${\displaystyle {A}_{i}}$ ${\displaystyle {A}_{j}}$

Стратификация

Недавно были предложены новые методы, основанные на концепции стратификации . ^[10] Начиная с проективной структуры, которая может быть рассчитана только из соответствий, усовершенствуйте эту проективную реконструкцию до евклидовой реконструкции, используя все доступные ограничения. С помощью этой идеи проблема может быть стратифицирована на различные разделы: в зависимости от количества доступных ограничений ее можно анализировать на другом уровне, проективном, аффинном или евклидовом.

Расслоение трехмерной геометрии

Обычно мир воспринимается как трехмерное евклидово пространство . В некоторых случаях невозможно использовать полную евклидову структуру трехмерного пространства. Простейшая из них — проективная, затем аффинная геометрия, которая образует промежуточные слои, и, наконец, евклидова геометрия. Понятие стратификации тесно связано с рядом преобразований геометрических объектов: в проективном страте — ряд проективных преобразований (гомография ) , в аффинном страте — ряд аффинных преобразований , а в евклидовом страте — ряд евклидовых преобразований.

Предположим, что фиксированная сцена захвачена двумя или более перспективными камерами, и соответствия между видимыми точками на разных изображениях уже даны. Однако на практике сопоставление является существенной и чрезвычайно сложной проблемой в компьютерном зрении. Здесь мы предполагаем, что 3D-точки наблюдаются камерами с проекционными матрицами. Ни положение точки, ни проекция камеры не известны. Известны только проекции точки на изображении. ${\displaystyle n}$ ${\displaystyle A_{i}}$ ${\displaystyle m}$ ${\displaystyle P_{j},j=1,\ldots ,m.}$ ${\displaystyle a_{ij}}$ ${\displaystyle i^{th}}$ ${\displaystyle j^{th}}$

Проективная реконструкция

Простой подсчет показывает, что у нас есть независимые измерения и только неизвестные, поэтому задача должна быть разрешима с достаточным количеством точек и изображений. Уравнения в однородных координатах можно представить следующим образом: ${\displaystyle 2nm}$ ${\displaystyle 11m+3n}$

${\displaystyle a_{ij}\sim P_{j}A_{i}\qquad i=1,\ldots n,~~j=1,\ldots m}$ (2)

Таким образом, мы можем применить невырожденное преобразование 4 × 4 H к проекциям → и мировым точкам → . Следовательно, без дополнительных ограничений, реконструкция представляет собой лишь неизвестную проективную деформацию трехмерного мира. ${\displaystyle P_{j}}$ ${\displaystyle P_{j}H^{-1}}$ ${\displaystyle A_{i}}$ ${\displaystyle HA_{i}}$

Аффинная реконструкция

Более подробную информацию о вычислении положения плоскости на бесконечности см . в разделе аффинное пространство ${\displaystyle {\Pi }_{\infty }}$ . Самый простой способ — использовать имеющиеся знания, например, информацию о том, что линии на сцене параллельны или что точка находится на расстоянии одной трети между двумя другими.

Мы также можем использовать априорные ограничения на движение камеры. Анализируя различные изображения одной и той же точки, можно получить линию в направлении движения. Пересечение нескольких линий — это точка на бесконечности в направлении движения, и одно ограничение на аффинную структуру.

Евклидова реконструкция

Отображая проективную реконструкцию в ту, которая удовлетворяет группе избыточных евклидовых ограничений, мы можем найти проективное преобразование H в уравнении (2). Уравнения являются сильно нелинейными, и требуется хорошее начальное предположение для структуры. Это может быть получено путем предположения линейной проекции - параллельной проекции, что также позволяет легко реконструировать с помощью разложения SVD. ^[2]

Алгебраическая и геометрическая ошибка

Неизбежно, измеренные данные (т. е. положение точек изображения или мира) зашумлены, и шум исходит из многих источников. Чтобы уменьшить влияние шума, мы обычно используем больше уравнений, чем необходимо, и решаем с помощью наименьших квадратов .

Например, в типичной формулировке задачи нулевого пространства Ax = 0 (например, алгоритм DLT) квадрат остатка ||Ax|| минимизируется с помощью метода наименьших квадратов.

В общем случае, если ||Ax|| можно рассматривать как расстояние между геометрическими объектами (точками, прямыми, плоскостями и т. д.), то минимизируется геометрическая ошибка , в противном случае (когда ошибка не имеет хорошей геометрической интерпретации) она называется алгебраической ошибкой .

Поэтому, по сравнению с алгебраической ошибкой, мы предпочитаем минимизировать геометрическую ошибку по перечисленным причинам:

1. Минимизируемое количество имеет смысл.
2. Решение более стабильное.
3. Решение постоянно относительно евклидовых преобразований.

Все линейные алгоритмы (DLT и другие), которые мы видели до сих пор, минимизируют алгебраическую ошибку. На самом деле, нет никаких оправданий для минимизации алгебраической ошибки, кроме простоты реализации, поскольку это приводит к линейной проблеме. Минимизация геометрической ошибки часто является нелинейной проблемой, которая допускает только итерационные решения и требует отправной точки.

Обычно линейное решение, основанное на алгебраических остатках, служит отправной точкой для нелинейной минимизации геометрической функции стоимости, что обеспечивает решению окончательную «полировку». ^[11]

Медицинские приложения

2-D визуализация имеет проблемы анатомии, накладывающейся друг на друга, и не раскрывает аномалии. 3-D визуализация может использоваться как в диагностических, так и в терапевтических целях.

3-D модели используются для планирования операции, морфометрических исследований и имеют большую надежность в ортопедии. ^[12]

Проекция P на обе камеры

Постановка проблемы и основы

Для реконструкции 3D-изображений из 2D-изображений, полученных камерой под разными углами. Медицинские методы визуализации, такие как КТ и МРТ, являются дорогостоящими, и хотя КТ-сканирование является точным, оно может вызывать высокие дозы облучения, что является риском для пациентов с определенными заболеваниями. Методы, основанные на МРТ, не являются точными. Поскольку во время МРТ мы подвергаемся воздействию мощных магнитных полей, этот метод не подходит для пациентов с ферромагнитными металлическими имплантатами. Оба метода можно применять только в положении лежа, когда изменяется глобальная структура кости. Поэтому мы обсудим следующие методы, которые можно применять стоя и которые требуют низкой дозы облучения.

Хотя эти методы представляют собой трехмерную визуализацию, интересующая область ограничена срезом; данные собираются для формирования временной последовательности.

Методика, основанная на стереосоответствующих точках

Этот метод прост и реализуется путем ручного определения точек на многопроекционных рентгенограммах. Первым шагом является извлечение соответствующих точек на двух рентгеновских снимках. Вторым шагом является реконструкция изображения в трех измерениях с использованием алгоритмов, таких как дискретное линейное преобразование (DLT). ^[13] Реконструкция возможна только при наличии стерео соответствующих точек (SCP). Качество результатов зависит от количества SCP, чем больше SCP, тем лучше результаты ^[14] , но это медленно и неточно. Навыки оператора являются фактором качества изображения. Методы, основанные на SCP, не подходят для костных структур без идентифицируемых краев. Как правило, методы, основанные на SCP, используются как часть процесса, включающего другие методы. ^[15]

Метод нестерео соответствующего контура (NCSS)

Этот метод использует рентгеновские снимки для трехмерной реконструкции и разработки трехмерных моделей с низкой дозой облучения в положениях с весовой нагрузкой.

В алгоритме NSCC предварительным шагом является расчет начального решения. Во-первых, определяются анатомические области из общего объекта. Во-вторых, выполняется ручная идентификация 2D-контуров на рентгенограммах. Из каждой рентгенограммы генерируются 2D-контуры с использованием 3D-объекта начального решения. 3D-контуры поверхности начального объекта проецируются на связанную с ними рентгенограмму. ^[15] 2D-ассоциация, выполняемая между этими 2 заданными точками, основана на расстояниях от точки до точки и выводах контуров, разрабатывающих соответствие между 2D-контурами и 3D-контурами. Следующий шаг — оптимизация начального решения. Наконец, деформация оптимизированного решения выполняется путем применения алгоритма Кригинга к оптимизированному решению. ^[16] Наконец, путем итерации последнего шага до тех пор, пока расстояние между двумя заданными точками не превзойдет заданное значение точности, получается реконструированный объект.

Преимущество этого метода в том, что его можно использовать для костных структур непрерывной формы, а также он сокращает вмешательство человека, но он отнимает много времени.

Техника поверхностной визуализации

Рендеринг поверхности визуализирует 3D-объект как набор поверхностей, называемых изоповерхностями. Каждая поверхность имеет точки с одинаковой интенсивностью (называемой изо-значением). Этот метод обычно применяется к высококонтрастным данным и помогает иллюстрировать отдельные структуры; например, череп может быть создан из срезов головы, а кровеносная система — из срезов тела. Два основных метода:

• Реконструкция на основе контуров: изоконтуры прикрепляются друг к другу, образуя изоповерхности. ^[17]
• Реконструкция на основе вокселей: воксели с одинаковым значением интенсивности используются для формирования изоповерхностей. Популярные алгоритмы — Marching Cubes, Marching Tetrahedrons и Dividing Cubes. ^[17]

Другие методы используют статистические модели формы, параметрические модели или гибриды этих двух методов.

Смотрите также

• Оценка 3D-позы  – процесс определения пространственных характеристик объектов
• 3D-реконструкция  – процесс запечатления формы и внешнего вида реальных объектов.
• 3D фотография
• Преобразование 2D в 3D  – процесс преобразования 2D-фильма в 3D-форму.
• Сбор 3D-данных и реконструкция объектов  – сканирование объекта или среды для сбора данных о его форме.
• Эпиполярная геометрия  – Геометрия стереозрения
• Резекция камеры  – процесс оценки параметров модели камеры-обскуры
• Компьютерное стереозрение  – Извлечение 3D-данных из цифровых изображений
• Структура из движения  – Метод 3D-реконструкции из движущихся объектов
• Сравнение программного обеспечения для фотограмметрии
• Визуальная оболочка  – это геометрическая сущность, созданная методом «форма-из-силуэта».Страницы, отображающие описания викиданных в качестве резерва
• Синтез изображений человека  – Компьютерная генерация изображений человека

Ссылки

1. "Soltani, AA, Huang, H., Wu, J., Kulkarni, TD, & Tenenbaum, JB Синтез 3D-фигур с помощью моделирования многоракурсных карт глубины и силуэтов с помощью глубоких генеративных сетей. В трудах конференции IEEE по компьютерному зрению и распознаванию образов (стр. 1511-1519)". GitHub . 6 марта 2020 г.
2. C. Tomasi и T. Kanade, «Форма и движение из потоков изображений при орфографии: подход факторизации», International Journal of Computer Vision, 9(2):137-154, 1992.
3. А. Лаурентини (февраль 1994 г.). «Концепция визуальной оболочки для понимания изображений на основе силуэтов». Труды IEEE по анализу образов и машинному интеллекту . 16 (2): 150–162. doi :10.1109/34.273735.
4. Р. Мор и Э. Арбогаст. Это можно сделать без калибровки камеры. Pattern Recognition Letters, 12:39-43, 1991.
5. О. Фожерас. Что можно увидеть в трех измерениях с помощью некалиброванной стереоустановки? В Трудах Европейской конференции по компьютерному зрению, страницы 563-578, Санта-Маргерита Л., 1992.
6. Э. Круппа. Zur Ermittlung eines Objektes aus zwei Perspectiven mit Internal Orientierung. Ситц.-Бер.Акад.Висс., Вена, мат. природа. Кл., абт. IIa., 122:1939-1948, 1913.
7. SJ Maybank и O. Faugeras. Теория самокалибровки движущейся камеры. International Journal of Computer Vision, 8(2):123-151, 1992.
8. О. Фогерас и С. Мейбанк. Движение из точек совпадений: множественность решений. International Journal of Computer Vision, 4(3):225-246, июнь 1990 г.
9. RI Hartley. Уравнения Круппы, полученные из фундаментальной матрицы Архивировано 22 июня 2018 г. в Wayback Machine . Труды IEEE по анализу шаблонов и машинному интеллекту, 19(2):133-135, февраль 1997 г.
10. Поллефейс, Марк. Самокалибровка и метрическая 3D-реконструкция из некалиброванных последовательностей изображений. Дисс. докторская диссертация, ESAT-PSI, KU Leuven, 1999.
11. Р. Хартли и А. Зиссерман. Многовидовая геометрия в компьютерном зрении. Cambridge University Press, 2-е издание, 2003.
12. «Медицинская визуализация: что это и для чего она нужна?». GarageFarm . 2018-02-18 . Получено 2018-02-18 .
13. "Pearcy MJ. 1985. Стереорентгенография движения поясничного отдела позвоночника. Acta Orthop Scand Suppl".
14. "Aubin CE, Dansereau J, Parent F, Labelle H, de Guise JA. 1997. Морфометрические оценки персонализированных 3D-реконструкций и геометрических моделей позвоночника человека". Med Biol Eng Comput .
15. "С.Хосейниан, Х.Арефи, 3D-реконструкция по многопроекционным медицинским рентгеновским изображениям. Обзор и оценка существующих методов" (PDF) .
16. Laporte, S; Skalli, W; de Guise, JA; Lavaste, F; Mitton, D (2003). «Метод бипланарной реконструкции на основе 2D и 3D контуров: применение к дистальному отделу бедренной кости». Comput Methods Biomech Biomed Engin . 6 (1): 1–6. doi :10.1080/1025584031000065956. PMID  12623432. S2CID  3206752.
17. G.Scott Owen, HyperVis. Комитет по образованию ACM SIGGRAPH, Национальный научный фонд (DUE-9752398) и Лаборатория гипермедиа и визуализации, Университет штата Джорджия .

Дальнейшее чтение

• Ясутака Фурукава и Карлос Эрнандес (2015) Многопросмотровое стерео: учебное пособие [1]
• Флинн, Джон и др. «Deepstereo: обучение прогнозированию новых видов на основе изображений мира». Труды конференции IEEE по компьютерному зрению и распознаванию образов. 2016.

Внешние ссылки

• 3D-реконструкция из нескольких изображений — обсуждаются методы извлечения 3D-моделей из простых изображений.
• Визуальное 3D-моделирование по изображениям и видео — технический отчет, описывающий теорию, практику и приемы 3D-реконструкции по изображениям и видео.
• Синтез 3D-фигур посредством моделирования многоракурсных карт глубины и силуэтов с помощью глубоких генеративных сетей. Создавайте и реконструируйте 3D-фигуры посредством моделирования многоракурсных карт глубины или силуэтов.