Стержневое исчисление

Метод расчета, используемый в Древнем Китае

Стержневое исчисление или стержневое исчисление было механическим методом алгоритмических вычислений с использованием счетных стержней в Китае от Воюющих царств до династии Мин до того, как счетные стержни были все больше заменены более удобными и быстрыми счетами . Стержневое исчисление играло ключевую роль в развитии китайской математики до ее расцвета в династиях Сун и Юань , достигнув кульминации в изобретении полиномиальных уравнений с числом неизвестных до четырех в работе Чжу Шицзе .

Японская счетная доска с сетками

Факсимиле стержневого исчисления из энциклопедии Юнлэ

Аппаратное обеспечение

Основное оборудование для проведения стержневого исчисления — это связка счетных стержней и счетная доска. Счетные стержни обычно изготавливаются из бамбуковых палочек длиной около 12–15 см, диаметром от 2 до 4 мм, иногда из костей животных или слоновой кости и нефрита (для состоятельных торговцев). Счетная доска может быть столешницей, деревянной доской с сеткой или без нее, на полу или на песке.

В 1971 году китайские археологи обнаружили связку хорошо сохранившихся счетных палочек из костей животных, хранившихся в шелковом мешочке в гробнице в уезде Цянь Ян провинции Шаньси, датируемой первой половиной династии Хань (206 г. до н.э. – 8 г. н.э.). ^{[ необходима цитата ]} В 1975 году была обнаружена связка бамбуковых счетных палочек. ^{[ необходима цитата ]}

Использование счетных стержней для стержневого исчисления процветало в эпоху Воюющих царств , хотя археологических артефактов, относящихся к периоду ранее династии Западная Хань (первая половина династии Хань ), обнаружено не было ; однако археологи обнаружили программные артефакты стержневого исчисления, датируемые периодом Воюющих царств . Поскольку программное обеспечение стержневого исчисления должно было существовать вместе с аппаратным обеспечением стержневого исчисления, нет сомнений в том, что стержневое исчисление процветало уже в эпоху Воюющих царств, более 2200 лет назад.

Программное обеспечение

Основным программным обеспечением, необходимым для исчисления с помощью стержней, была простая позиционная десятичная таблица умножения из 45 фраз, которая использовалась в Китае с древних времен и называлась таблицей «девять на девять» . Ее заучивали наизусть ученики, торговцы, правительственные чиновники и математики.

Стержневые цифры

Отображение чисел

Две формы китайских стержневых цифр

Представление числа 231 и возможные вводящие в заблуждение расположения стержней.

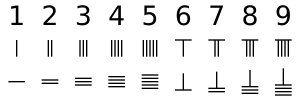
Стержневые цифры — единственная числовая система, которая использует различные комбинации размещения одного символа для передачи любого числа или дроби в десятичной системе. Для чисел в разряде единиц каждый вертикальный стержень представляет 1. Два вертикальных стержня представляют 2 и так далее, пока не останется 5 вертикальных стержней, что представляет 5. Для чисел от 6 до 9 используется биквинарная система, в которой горизонтальная черта над вертикальными чертами представляет 5. Первый ряд — это числа от 1 до 9 в стержневых цифрах, а второй ряд — те же числа в горизонтальной форме.

Для чисел больше 9 используется десятичная система . Стержни, расположенные на одну позицию левее единицы, представляют 10 раз больше этого числа. Для сотен слева размещается другой набор стержней, который представляет 100 раз больше этого числа, и так далее. Как показано на соседнем изображении, число 231 представлено в виде стержневых цифр в верхнем ряду, причем один стержень в разряде единиц представляет 1, три стержня в разряде десятков представляют 30, а два стержня в разряде сотен представляют 200, с суммой 231.

При выполнении расчетов, как правило, на поверхности не было сетки. Если стержневые цифры два, три и один размещаются последовательно в вертикальной форме, есть вероятность, что их ошибочно примут за 51 или 24, как показано во втором и третьем ряду соседнего изображения. Чтобы избежать путаницы, числа в последовательных местах размещаются в чередующейся вертикальной и горизонтальной форме, а единицы размещаются в вертикальной форме, ^[1], как показано в нижнем ряду справа.

Отображение нулей

В родовых числах нули представлены пробелом, который служит как числом, так и значением-заполнителем. В отличие от индо-арабских цифр , нет специального символа для представления нуля. До введения письменного нуля, в дополнение к пробелу для указания отсутствия единиц, символ в последующем столбце единиц поворачивался на 90°, чтобы уменьшить неоднозначность одного нуля. ^[2] Например, 107 (𝍠 𝍧) и 17 (𝍩𝍧) будут различаться поворотом, в дополнение к пробелу, хотя несколько нулевых единиц могут привести к неоднозначности, например, 1007 (𝍩 𝍧) и 10007 (𝍠 𝍧). На соседнем изображении число ноль представлено просто пробелом.

Отрицательные и положительные числа

Математики Сонга использовали красный цвет для обозначения положительных чисел и черный для отрицательных чисел . Однако, другой способ — добавить косую черту в последнюю позицию, чтобы показать, что число отрицательное. ^[3]

Десятичная дробь

Математический трактат Суньцзы использовал метрологию десятичных дробей. Единицей длины была 1 чи ,

1 ци = 10 цунь , 1 цунь = 10 фэнь , 1 фэнь = 10 ли , 1 ли = 10 хао , 10 хао = 1 ши, 1 ши = 10 ху .

1 чи 2 цунь 3 фэнь 4 ли 5 ​​хао 6 ши 7 ху разложены на счетной доске как

где единица измерения хи .

Математик династии Южная Сун Цинь Цзюшао расширил использование десятичной дроби за пределы метрологии. В своей книге «Математический трактат в девяти разделах » он формально выразил 1,1446154 дня как

日

Он обозначил единицу словом «日» (день) под ней. ^[4]

Добавление

Сложение стержневого исчисления 3748+289=4037

Стержневое исчисление работает по принципу сложения. В отличие от арабских цифр , цифры, представленные счетными стержнями, обладают аддитивными свойствами. Процесс сложения включает механическое перемещение стержней без необходимости запоминания таблицы сложения . Это самое большое отличие от арабских цифр, так как нельзя механически сложить 1 и 2, чтобы получить 3, или 2 и 3, чтобы получить 5.

На соседнем изображении показаны шаги сложения 3748 и 289:

1. Поместите слагаемое 3748 в первую строку, а слагаемое 289 — во вторую.
2. Вычислите СЛЕВА НАПРАВО, начиная с 2 из 289.
3. Уберите два стержня снизу и добавьте 7 сверху, чтобы получилось 9.
4. Переместите 2 стержня сверху вниз на 8, перенесите один вперед на 9, который станет нулём, и перенесите на 3, чтобы получить 4, удалите 8 из нижнего ряда.
5. Переместите один стержень с 8-го ряда в верхний ряд на 9-й в нижний, чтобы перенести один на следующий ряд, и добавьте один стержень к 2-м стержням в верхнем ряду, чтобы получилось 3 стержня, верхний ряд слева — 7.
6. Результат 3748+289=4037

Стержни в слагаемом меняются в ходе сложения, тогда как стержни в слагаемом внизу «исчезают».

Вычитание

Без заимствований

В ситуации, когда заимствование не требуется, нужно только взять количество стержней в вычитаемом из уменьшаемого . Результатом вычисления является разность. На соседнем изображении показаны шаги вычитания 23 из 54.

Заимствование

В ситуациях, когда требуется заимствование, например, 4231–789, необходимо использовать более сложную процедуру. Шаги для этого примера показаны слева.

1. Поместите уменьшаемое 4231 сверху, вычитаемое 789 снизу. Вычисляйте слева направо.
2. Заимствуем 1 из разряда тысяч для получения десятки в разряде сотен, минус 7 из ряда ниже, разность 3 прибавляем к 2 сверху, получая 5. 7 снизу вычитаем, что показано пробелом.
3. Заимствуем 1 из разряда сотен, и получаем 4. 10 в разряде десятков минус 8 внизу дает 2, которое прибавляется к 3 вверху, образуя 5. Верхний ряд теперь равен 3451, нижний — 9.
4. Заимствуем 1 из 5 в разряде десятков сверху, что оставляет 4. 1, заимствованная из разряда десятков, равна 10 в разряде единиц, вычитаем 9, что дает 1, которая добавляется сверху, чтобы получить 2. После вычитания всех стержней в нижнем ряду, 3442 в верхнем ряду составляет результат вычисления

Умножение

38x76=2888

аль Уклидис (952 г. н.э.) умножение, вариант умножения Сунзи

Сунцзы Суаньцзин подробно описал алгоритм умножения. Слева приведены шаги для вычисления 38×76:

1. Множимое поместите сверху, множитель снизу. Совместите разряд единиц множителя с самым высоким разрядом множимого. Оставьте место в середине для записи.
2. Начните вычисление с самого высокого разряда множимого (в примере вычислите 30×76, а затем 8×76). Используя таблицу умножения, 3 раза по 7 будет 21. Поместите 21 в палочки посередине, совместив 1 с десятками множителя (сверху 7). Затем, 3 раза по 6 равно 18, поместите 18, как показано на рисунке. После того, как 3 в множимом полностью умножено, уберите палочки.
3. Переместите множитель на одну позицию вправо. Измените 7 на горизонтальную форму, 6 на вертикальную.
4. 8×7 = 56, поместите 56 во второй ряд посередине, совместив единицы с цифрами, умноженными в множителе. Вычтите 7 из множителя, так как он был умножен.
5. 8×6 = 48, 4 прибавляется к 6 последнего шага, получается 10, переносится 1. Вычитаем 8 из разряда единиц в множимом и вычитаем 6 из разряда единиц множимого.
6. Сложите 2380 и 508 в середине, и получится 2888: произведение.

Разделение

10-й век аль-Уклидис раздел

Подразделение Сунзи ⁠309/7⁠ = 44 ⁠1/7⁠

Деление аль-Хорезми 825 г. н.э. было идентично алгоритму деления Сунзи

Дивизия Кушьяра ибн Лаббана XI века, точная копия дивизии Сунзи.

Анимация слева показывает шаги расчета ⁠309/7⁠ = 44 ⁠1/7⁠ .

1. Поместите делимое 309 в средний ряд, а делитель 7 в нижний ряд. Оставьте место для верхнего ряда.
2. Переместите делитель 7 на одну позицию влево, придав ему горизонтальную форму.
3. Используя китайскую таблицу умножения и деления, 30÷7 равно 4 и остатку 2. Поместите частное, 4, в верхнюю строку, а остаток, 2, в среднюю строку.
4. Переместите делитель на одну позицию вправо, изменив его на вертикальную форму. 29÷7 равно 4 остатку 1. Поместите частное, 4, сверху, оставив делитель на месте. Поместите остаток в среднюю строку вместо делимого на этом шаге. Результатом является частное 44 с остатком 1

Алгоритм деления Сунзи был передан в полном объеме аль-Хорезми в исламские страны из индийских источников в 825 году нашей эры. Книга Аль-Хорезми была переведена на латынь в 13 веке. Алгоритм деления Сунзи позже развился в деление Галлея в Европе. Алгоритм деления в книге Абу-ль-Хасана аль-Уклидиси 925 года нашей эры «Китаб аль-Фусул фи аль-Хисаб аль-Хинди» и в книге Кушьяра ибн Лаббана 11 века «Принципы индуистского исчисления» были идентичны алгоритму деления Сунзу.

Дроби

Если при делении десятичной дроби с позиционным значением получается остаток, то и остаток, и делитель должны быть оставлены на месте друг над другом. В заметках Лю Хуэя к Цзючжан суаньшу (II в. до н. э.) число сверху называется «ши» (实), а число снизу называется «фа» (法). В «Суньцзы суаньцзин » число сверху называется «цзы» (子) или «фэньцзы» (дословно «сын дроби»), а число снизу называется «му» (母) или «фэньму» (дословно «мать дроби»). Фэньцзы и Фэньму также являются современными китайскими названиями числителя и знаменателя соответственно. Как показано справа, 1 — остаток числителя, 7 — делитель знаменателя, образовавшие дробь ⁠1/7⁠ . Частное от деления ⁠309/7⁠ 44 + ⁠1/7⁠ . Лю Хуэй использовал много вычислений с дробями в «Хайдао Суаньцзин» .

Эта форма дроби с числителем сверху и знаменателем снизу без горизонтальной черты между ними была передана в арабские страны в книге аль-Хорезми 825 г. н. э. через Индию и использовалась в X веке Абуль-Хасаном аль-Уклидиси и в XV веке Джамшидом аль-Каши в его труде «Арифметический ключ».

Добавление

исчисление стержней дробь сложение

⁠1/3⁠ + ⁠2/5⁠

• Поместите два числителя 1 и 2 на левую сторону счетной доски, поместите два знаменателя 3 и 5 на правую сторону.
• Умножьте крест-накрест 1 на 5, 2 на 3, чтобы получить 5 и 6, замените числители соответствующими перекрестными произведениями.
• Умножьте два знаменателя 3 × 5 = 15, поместите в правом нижнем углу.
• Сложите два числителя 5 и 6 = 11, записанное в правом верхнем углу счетной доски.
• Результат: ⁠1/3⁠ + ⁠2/5⁠ = ⁠11/15⁠

Вычитание

вычитание двух стержневых числовых дробей

⁠8/9⁠ − ⁠1/5⁠

• Запишите цифру стержня для числителей 1 и 8 с левой стороны счетной доски.
• Положите палочки для знаменателей 5 и 9 с правой стороны счетной доски.
• Перемножьте крест-накрест 1 × 9 = 9, 5 × 8 = 40, замените соответствующие числители
• Умножьте знаменатели 5 × 9 = 45, поместите 45 в правый нижний угол счетной доски, замените знаменатель 5
• Вычтите 40 − 9 = 31, поместите вверху справа.
• Результат: ⁠8/9⁠ − ⁠1/5⁠ = ⁠31/45⁠

Умножение

исчисление стержней дробь умножение

3 ⁠1/3⁠ × 5 ⁠2/5⁠

• Расположите счетные палочки на 3 ⁠1/3⁠ и 5 ⁠2/5⁠ на счетной доске в формате табуляции шан, ши, фа.
• шан умножить на фа добавить к ши: 3 × 3 + 1 = 10; 5 × 5 + 2 = 27
• ши умножить на ши:10 × 27 = 270
• fa умножить на fa:3 × 5 = 15
• ши делится на фа: 3 ⁠1/3⁠ × 5 ⁠2/5⁠ = 18

Наибольший общий делитель и сокращение дроби

наибольший общий делитель

Алгоритм нахождения наибольшего общего множителя двух чисел и сокращения дроби был изложен в Цзючжан суаньшу . Наибольшая общая делитель находится путем последовательного деления с остатками до тех пор, пока последние два остатка не станут идентичными. Анимация справа иллюстрирует алгоритм нахождения наибольшего общего множителя ⁠32,450,625/59,056,400⁠ и сокращение дроби.

В этом случае hcf равен 25.

Разделите числитель и знаменатель на 25. Сокращенная дробь равна ⁠1,298,025/2,362,256⁠ .

Интерполяция

π в дроби

Календарь и математик Хэ Чэнтянь (何承天) использовал метод интерполяции дробей , называемый «гармонизацией делителя дня» (调日法), чтобы получить лучшее приближенное значение, чем старое, путем итеративного сложения числителей и знаменателей «слабой» дроби с «сильной» дробью. ^[5] Легендарное π = ⁠ Цзу Чунчжи355/113⁠ можно получить с помощью метода Хэ Чэнтяня ^[6]

Система линейных уравнений

системные уравнения

Глава восьмая Прямоугольные массивы Цзючжана Суаньшу предоставил алгоритм решения Системы линейных уравнений методом исключения : ^[7]

Задача 8-1: Предположим, что у нас есть 3 пачки круп высшего качества, 2 пачки круп среднего качества и пачка круп низкого качества совокупным весом 39 доу. У нас также есть 2, 3 и 1 пачка соответствующих круп общим весом 34 доу; у нас также есть 1, 2 и 3 пачки соответствующих круп общим весом 26 доу.

Найдите количество круп высшего, среднего и низкого качества. В алгебре эту задачу можно выразить тремя системами уравнений с тремя неизвестными.

${\displaystyle {\begin{cases}3x+2y+z=39\\2x+3y+z=34\\x+2y+3z=26\end{cases}}}$

Эта задача была решена в Цзючжан суаньшу с помощью счетных палочек, разложенных на счетной доске в табличном формате, похожем на матрицу 3x4:

Алгоритм:

1. Умножьте центральный столбец на наивысшее число качества в правом столбце.
2. Повторно вычитайте правый столбец из центрального столбца, пока верхнее число центрального столбца не станет равным 0.
3. умножьте левый столбец на значение верхней строки правого столбца.
4. Повторно вычитайте правый столбец из левого столбца, пока верхнее число левого столбца не станет равным 0.
5. После применения вышеописанного алгоритма исключения к уменьшенному центральному столбцу и левому столбцу матрица была приведена к треугольной форме.

Количество одной пачки некачественной крупы ${\displaystyle ={\frac {99}{36}}=2{\frac {3}{4}}}$

Из чего можно легко узнать количество одной пачки круп высшего и среднего качества:

• Одна пачка высококачественных злаков = 9 доу ${\displaystyle {\frac {1}{4}}}$
• Одна пачка хлопьев среднего размера = 4 доу ${\displaystyle {\frac {1}{4}}}$

Извлечение квадратного корня

Алгоритм извлечения квадратного корня описан в «Цзючжан суаньшу» и с небольшими различиями в терминологии в «Суньцзы суаньцзин» .

извлечение квадратного корня из 234567 в Sunzi Suanjing

извлечение квадратного корня Кушьяром ибн Лаббаном

Анимация демонстрирует алгоритм извлечения приближенного квадратного корня с помощью стержневого исчисления из алгоритма в задаче 19 главы 2 Суньцзы Суаньцзина: ${\displaystyle {\sqrt {234567}}\approx 484{\tfrac {311}{968}}}$

Теперь есть квадрат площадью 234567, найдите одну сторону квадрата . ^[8]

Алгоритм следующий:

• Установите 234567 на счетной доске, во втором ряду сверху, назовите его ши
• Установите маркер 1 на позицию 10000 в 4-м ряду с именем xia fa.
• Оцените первую цифру квадратного корня как счетную палочку цифрой 4, поместите ее в верхний ряд ( шанг ) в позицию сотен,
• Умножьте шан 4 на сяфа 1, поместите результат 4 в 3-й ряд под названием фан фа.
• Умножаем шан на фан фа, вычитаем произведение 4x4=16 из ши : 23-16=7, остается цифра 7.
• удвойте фан фа 4, чтобы получить 8, сдвиньте на одну позицию вправо и измените вертикальную 8 на горизонтальную 8 после перемещения вправо.
• Переместите ся фа на две позиции вправо.
• Оцените вторую цифру слова шан как 8: поместите цифру 8 на десятую позицию в верхнем ряду.
• Умножаем ся фа на новую цифру шан , прибавляем к фан фа

.

• 8 называет 8 = 64, вычитаем 64 из цифры верхнего ряда «74», оставляя одну палочку на самой значимой цифре.
• удвоить последнюю цифру fang fa 8, добавить к 80 = 96
• Переместите fang fa 96 на одну позицию вправо, измените условное обозначение; переместите xia fa "1" на две позиции вправо.
• Оцените третью цифру слова шан как 4.
• Умножьте новую цифру шан 4 на ся фа 1 и объедините с фан фа , чтобы получить 964.
• вычтите последовательно 4*9=36,4*6=24,4*4=16 из ши , оставив 311
• удвоить последнюю цифру 4 слова fang fa, чтобы получить 8, и объединить с fang fa
• результат ${\displaystyle {\sqrt {234567}}\approx 484{\tfrac {311}{968}}}$

Математик династии Северная Сун Цзя Сянь разработал аддитивный мультипликативный алгоритм для извлечения квадратного корня , в котором он заменил традиционное «удвоение» «фан фа» добавлением цифры шан к цифре фан фа , с тем же эффектом.

Извлечение кубического корня

Аддитивный мультипликативный метод извлечения кубического корня Цзя Сяня

В четвертом томе «Шаогуан» Цзючжан суаньшу представлен алгоритм извлечения кубического корня.

〔一九〕今有積一百八十六萬八百六十七尺。問為立方幾何？答曰:一百二十三尺。

Задача 19: У нас есть кубический хи размером 1860867, какова длина стороны? Ответ: 123 хи.

${\displaystyle {\sqrt[{3}]{1860867}}=123}$

Математик династии Северная Сун Цзя Сянь изобрел метод, похожий на упрощенную форму схемы Горнера для извлечения кубического корня. Анимация справа показывает алгоритм Цзя Сяня для решения задачи 19 в Цзючжан суаньшу том 4.

Полиномиальное уравнение

Алгоритм «Хорнера» Цинь Цзюшао

Математик династии Северная Сун Цзя Сянь изобрел схему Горнера для решения простого уравнения 4-го порядка вида

${\displaystyle x^{4}=a}$

Математик династии Южная Сун Цинь Цзюшао улучшил метод Горнера Цзя Сяня для решения полиномиальных уравнений до 10-го порядка. Ниже приведен алгоритм решения

${\displaystyle -x^{4}+15245x^{2}-6262506.25=0}$в его «Математическом трактате в девяти разделах», том 6, задача 2. ^[9]

Это уравнение было составлено снизу вверх с помощью счетных палочек на счетной доске в табличной форме.

Алгоритм:

1. Расположите коэффициенты в табличной форме, константа при ши, коэффициент при х при шан лянь, коэффициент при и ${\displaystyle x^{4}}$ юй; выровняйте числа по рангу единиц.
2. Продвинуться на два ряда Шан Лянь
3. Продвиньтесь на три ступени yi yu
4. Оценка шанг=20
5. пусть ся лянь = шан * и юй
6. пусть фу лянь=шан *йи юй
7. объединить фу лянь с шан лянь
8. пусть фан=шан * шан лянь
9. вычтите шан*фан из ши
10. добавить шан * и юй к ся лянь
11. уберите Ся Лянь на 3 ранга, уберите И Юй на 4 ранга
12. Вторая цифра слова шан — 0.
13. объединить шан лянь в фан
14. объединить yi yu в xia lian
15. Добавьте yi yu к fu lian, вычтите результат из fang, пусть результат будет знаменателем.
16. найдите наибольший общий множитель =25 и упростите дробь ${\displaystyle {\frac {32450625}{59056400}}}$
17. решение ${\displaystyle x=20{\frac {1298205}{2362256}}}$

Тянь Юань шу

Тянь юань шу в Ли Чжи: Игу яньдуань

Математик династии Юань Ли Чжи развил стержневое исчисление в Тянь Юань Шу

Пример Ли Чжи Цэюань хайцзин т. II, задача 14, уравнение с одним неизвестным:

${\displaystyle -x^{2}-680x+96000=0}$

元

Полиномиальные уравнения с четырьмя неизвестными

Факсимиле Чжу Шицзе: Нефритовое зеркало четырех неизвестных

Математик Чжу Шицзе развил исчисление стержней, включив в него полиномиальные уравнения с 2–4 неизвестными.

Например, многочлены от трех неизвестных:

Уравнение 1: ${\displaystyle -y-z-y^{2}*x-x+xyz=0}$

Да

Уравнение 2: ${\displaystyle -y-z+x-x^{2}+xz=0}$

Уравнение 3: ${\displaystyle y^{2}-z^{2}+x^{2}=0;}$

Да

После последовательного исключения двух неизвестных полиномиальное уравнение трех неизвестных свелось к полиномиальному уравнению одного неизвестного:

${\displaystyle x^{4}-6x^{3}+4x^{2}+6x-5=0}$

Решено x=5;

Что игнорирует 3 других ответа, 2 из которых повторяются.

Смотрите также

• китайская математика
• Подсчет стержней

Ссылки

1. Ронан и Нидхэм, «Краткая наука и цивилизация в Китае», том 2, глава 1, Математика
2. "Китайские цифры". История математики . Получено 28.04.2024 .
3. * Хо Пэн Йоке, Ли, Ци и Шу ISBN 0-486-41445-0 
4. Лам Лэй Йонг, стр. 87-88
5. Жан Клод Марцлофф, История китайской математики, стр. 281
6. У Вэньцзюнь ред. Большая серия истории китайской математики т. 4 стр. 125
7. Жан-Клод Марцлофф, История китайской математики, стр. 249-257
8. Лэй Лэй Юн, Анг Тянь Се, Мимолетные шаги, стр. 66-73
9. Жан Клод Марцлофф, История китайской математики, стр. 233-246

• Лам Лэй Ён (蓝丽蓉) Анг Тянь Се (洪天赐), Мимолетные шаги, World Scientific ISBN 981-02-3696-4 
• Жан Клод Марцлофф, История китайской математики ISBN 978-3-540-33782-9