В математике и информатике шестнадцатеричная (также с основанием 16 или просто hex ) система счисления — это позиционная система счисления , которая представляет числа с использованием основания (основания) шестнадцать. В отличие от десятичной системы, представляющей числа с использованием десяти символов , шестнадцатеричная использует шестнадцать различных символов, чаще всего символы «0»–«9» для представления значений от 0 до 9 и «A»–«F» (или «a»–«f») для представления значений от десяти до пятнадцати.
Разработчики программного обеспечения и проектировщики систем широко используют шестнадцатеричные числа, поскольку они обеспечивают удобное представление двоично-кодированных значений. Каждая шестнадцатеричная цифра представляет четыре бита (двоичные цифры), также известные как полубайт (или ниббл). [1] Например, 6-битный байт может иметь значения в диапазоне от 000000 до 111111 (от 0 до 63 в десятичной системе) в двоичной форме, что может быть записано как от 00 до 3F в шестнадцатеричной системе.
В математике нижний индекс обычно используется для указания основания. Например, десятичное значение711 будет выражено в шестнадцатеричном виде как 2C7 16 . В программировании существует несколько обозначений для обозначения шестнадцатеричных чисел, обычно с использованием префикса. Префикс 0xиспользуется в C , который будет обозначать это значение как 0x2C7.
В кодировке Base 16 используется шестнадцатеричная система счисления , в которой каждый байт открытого текста разбивается на два 4-битных значения и представляется двумя шестнадцатеричными цифрами.
В большинстве современных вариантов использования буквы A–F или a–f представляют значения 10–15, тогда как цифры 0–9 используются для представления их десятичных значений.
Не существует универсальной конвенции об использовании нижнего или верхнего регистра, поэтому каждый из них распространен или предпочтителен в определенных средах по стандартам или конвенции сообщества; используется даже смешанный регистр. Некоторые семисегментные дисплеи используют смешанный регистр 'A b C d E F', чтобы отличать цифры A–F друг от друга и от 0–9.
Существует некоторая стандартизация использования пробелов (вместо запятых или других знаков препинания) для разделения шестнадцатеричных значений в длинном списке. Например, в следующем шестнадцатеричном дампе каждый 8-битный байт представляет собой 2-значное шестнадцатеричное число с пробелами между ними, в то время как 32-битное смещение в начале представляет собой 8-значное шестнадцатеричное число.
00000000 57 69 6b 69 70 65 64 69 61 2c 20 74 68 65 20 66 00000010 72 65 65 20 65 6e 63 79 63 6c 6f 70 65 64 69 61 00000020 20 74 68 61 74 20 61 6e 79 6f 6e 65 20 63 61 6e 00000030 20 65 64 69 74 0a В контекстах, где основание не ясно, шестнадцатеричные числа могут быть неоднозначными и путаться с числами, выраженными в других основаниях. Существует несколько соглашений для однозначного выражения значений. Числовой нижний индекс (сам записанный в десятичной системе) может явно указывать основание: 159 10 — это десятичное 159; 159 16 — это шестнадцатеричное 159, что равно 345 10 . Некоторые авторы предпочитают текстовый нижний индекс, например, 159 decimal и 159 hex или 159 d и 159 h .
Дональд Кнут в своей книге The TeXbook представил использование особого шрифта для представления определенного основания системы счисления . [2] Шестнадцатеричные представления записаны там шрифтом пишущей машинки : 5A3 , C1F27ED
В линейных текстовых системах, которые используются в большинстве сред компьютерного программирования, возникло множество методов:
0x, возможно, возник в системах IBM Stretch . Он произошел от 0префикса, уже использовавшегося для восьмеричных констант. Значения байтов могут быть выражены в шестнадцатеричном формате с префиксом, \xза которым следуют две шестнадцатеричные цифры: '\x1B'представляет управляющий символ Esc ; "\x1B[0m\x1B[25;1H"— строка, содержащая 11 символов с двумя встроенными символами Esc. [3] Для вывода целого числа в шестнадцатеричном формате с помощью семейства функций printf используется код преобразования формата %Xили .%xode;TxTFFh05A3H0FFhFFh0x42$в качестве префикса: $5A3, $C1F27ED.H'ABCD'(для ABCD 16 ). Аналогично, Fortran 95 использует Z'ABCD'.16#5A3#, 16#C1F27ED#. Для констант битового вектора VHDL использует обозначение x"5A3", x"C1F27ED". [6]8'hFF, где 8 — количество бит в значении, а FF — шестнадцатеричная константа.16r16r5A316#: 16#5A3, 16#C1F27ED.#xи #16r. Установка переменных *read-base* [7] и *print-base* [8] на 16 также может использоваться для переключения считывателя и принтера системы Common Lisp на шестнадцатеричное представление чисел для чтения и печати чисел. Таким образом, шестнадцатеричные числа могут быть представлены без кода префикса #x или #16r, когда входная или выходная база была изменена на 16.&H:&H5A3&для шестнадцатеричного кода. [10]0hпрефикс: 0h5A3,0hC1F27ED16r для обозначения шестнадцатеричных чисел используется префикс : 16r5a3, 16rC1F27ED. Двоичные, четверичные (основание 4) и восьмеричные числа могут быть заданы аналогичным образом.X'5A3'или X'C1F27ED', и он используется в Assembler, PL/I , COBOL , JCL , скриптах, командах и других местах. Этот формат был распространен и на других (и теперь устаревших) системах IBM. Иногда вместо апострофов использовались кавычки.Иногда известно, что числа имеют шестнадцатеричную систему счисления.
%: http://www.example.com/name%20with%20spacesгде %20— код символа пробела (пустого символа) , код ASCII 20 в шестнадцатеричном формате, 32 в десятичном формате.U+последующим шестнадцатеричным значением, например, U+00A1перевернутым восклицательным знаком (¡).#: например, пурпурный цвет#FF00FF представляется как . [11] CSS также допускает аббревиатуры из 3 шестнадцатеричных цифр с одной шестнадцатеричной цифрой на компонент: #FA3аббревиатуры #FFAA33(золотисто-оранжевый: ).=: Espa=F1a— это «España» ( шестнадцатеричный код F1 — это код для ñ в наборе символов ISO/IEC 8859-1). [12] )AA213FD51B3801043FBC ...:). Это, например, допустимый адрес IPv6: 2001:0db8:85a3:0000:0000:8a2e:0370:7334или сокращенно путем удаления начальных нулей как 2001:db8:85a3::8a2e:370:7334( Адреса IPv4 обычно записываются в десятичном виде).3F2504E0-4F89-41D3-9A0C-0305E82C3301.Использование букв от A до F для обозначения цифр выше 9 не было общепринятым на раннем этапе развития компьютеров.


Поскольку не было традиционных цифр для представления количеств от десяти до пятнадцати, в качестве замены были повторно использованы буквы алфавита. В большинстве европейских языков отсутствуют слова, не основанные на десятичной системе, для некоторых цифр от одиннадцати до пятнадцати. Некоторые люди читают шестнадцатеричные числа цифра за цифрой, как номер телефона, или используют фонетический алфавит НАТО , фонетический алфавит армии/флота или подобную специальную систему . После принятия шестнадцатеричной системы среди программистов IBM System/360 , Магнусон (1968) [23] предложил руководство по произношению, которое давало короткие названия буквам шестнадцатеричной системы — например, «A» произносилось как «ann», B — как «bet», C — как «chris» и т. д. [23] Другая система наименований была опубликована в Интернете Роджерсом (2007) [24] , который пытается сделать словесное представление различимым в любом случае, даже если фактическое число не содержит цифр A–F. Примеры приведены в таблицах ниже. Еще одна система именования была разработана Баббом (2015) на основе шутки из Кремниевой долины . [25]
Другие предложили использовать словесные соглашения азбуки Морзе для выражения четырехбитных шестнадцатеричных цифр, где «точка» и «тире» представляют ноль и единицу соответственно, так что «0000» озвучивается как «дит-дит-дит-дит» (....), да-дит-дит-да (-..-) озвучивает цифру со значением девять, а «да-да-да-да» (----) озвучивает шестнадцатеричную цифру для десятичного числа 15.

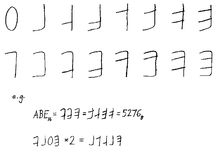
Системы счета по цифрам были разработаны как для двоичной, так и для шестнадцатеричной системы. Артур Кларк предложил использовать каждый палец как бит включения/выключения, что позволило вести счет от нуля до 1023 10 на десяти пальцах. [26] Другая система счета до FF 16 (255 10 ) проиллюстрирована справа.
Шестнадцатеричная система может выражать отрицательные числа так же, как и десятичная: −2A для представления −42 10 , −B01D9 для представления −721369 10 и так далее.
Шестнадцатеричное число также может использоваться для выражения точных битовых шаблонов, используемых в процессоре , поэтому последовательность шестнадцатеричных цифр может представлять знаковое или даже плавающее значение. Таким образом, отрицательное число −42 10 может быть записано как FFFF FFD6 в 32-битном регистре ЦП (в дополнительном коде ), как C228 0000 в 32-битном регистре FPU или C045 0000 0000 0000 в 64-битном регистре FPU (в стандарте IEEE с плавающей точкой ).
Так же, как десятичные числа могут быть представлены в экспоненциальной нотации , так же могут быть представлены и шестнадцатеричные числа. В нотации P используется буква P (или p , для «степени»), тогда как E (или e ) служит для той же цели в десятичной нотации E . Число после P является десятичным и представляет собой двоичную экспоненту. Увеличение экспоненты на 1 умножает на 2, а не на 16: 20p0 = 10p1 = 8p2 = 4p3 = 2p4 = 1p5 . Обычно число нормализуется таким образом, что шестнадцатеричные цифры начинаются с 1. (ноль обычно равен 0 без P ).
Пример: 1.3DEp42 представляет 1.3DE 16 × 2 42 10 .
Нотация P требуется двоичным стандартом с плавающей точкой IEEE 754-2008 и может использоваться для литералов с плавающей точкой в редакции C99 языка программирования C. [ 27] Используя спецификаторы преобразования %a или %A , эта нотация может быть получена реализациями семейства функций printf , следующих спецификации C99 [28] и стандарту Single Unix Specification (IEEE Std 1003.1) POSIX . [29]
.jpg/440px-Hewlett-Packard_Model_HP-16C_Programmable_RPN_Calculator,_HP's_First_and_Only_Calculator_esp._for_Programmers,_built_1982-1989_(edited_to_rectangular,_V2).jpg)
Большинство компьютеров оперируют двоичными данными, но людям сложно работать с большим количеством цифр даже для относительно небольшого двоичного числа. Хотя большинство людей знакомы с десятичной системой, гораздо проще преобразовать двоичную систему в шестнадцатеричную, чем в десятичную, поскольку каждая шестнадцатеричная цифра преобразуется в целое число бит (4 10 ). В этом примере число 1111 2 преобразуется в десятичную систему. Поскольку каждая позиция в двоичной системе может содержать либо 1, либо 0, ее значение можно легко определить по ее положению справа:
Поэтому:
При небольшой практике преобразование 1111 2 в F 16 за один шаг становится простым (см. таблицу в письменном виде). Преимущество использования шестнадцатеричной системы вместо десятичной быстро увеличивается с размером числа. Когда число становится большим, преобразование в десятичную систему становится очень утомительным. Однако при преобразовании в шестнадцатеричную систему тривиально рассматривать двоичную строку как 4-значные группы и преобразовывать каждую в одну шестнадцатеричную цифру. [30]
В этом примере показано преобразование двоичного числа в десятичное, сопоставление каждой цифры с десятичным значением и сложение результатов.
Сравните это с преобразованием в шестнадцатеричную систему счисления, где каждая группа из четырех цифр может рассматриваться независимо и преобразовываться напрямую:
Преобразование из шестнадцатеричной системы в двоичную также осуществляется напрямую. [30]
Хотя четверичная система счисления (основание 4) используется мало, ее можно легко преобразовать в шестнадцатеричную или двоичную систему счисления и обратно. Каждая шестнадцатеричная цифра соответствует паре четверичных цифр, а каждая четверичная цифра соответствует паре двоичных цифр. В приведенном выше примере 2 5 C 16 = 02 11 30 4 .
Восьмеричная (основание 8) система также может быть преобразована относительно легко, хотя и не так тривиально, как с основаниями 2 и 4. Каждая восьмеричная цифра соответствует трем двоичным цифрам, а не четырем. Таким образом, мы можем преобразовывать восьмеричную и шестнадцатеричную системы с помощью промежуточного преобразования в двоичную, а затем перегруппировывать двоичные цифры в группы по три или четыре.
Как и для всех оснований, существует простой алгоритм для преобразования представления числа в шестнадцатеричное посредством выполнения операций целочисленного деления и остатка в исходном основании. Теоретически это возможно для любого основания, но для большинства людей только десятичное, а для большинства компьютеров только двоичное (которое можно преобразовать гораздо более эффективными методами) может быть легко обработано этим методом.
Пусть d — число, которое нужно представить в шестнадцатеричной системе счисления, а ряд h i h i−1 ...h 2 h 1 — шестнадцатеричные цифры, представляющие это число.
«16» можно заменить любой другой базой по желанию.
Ниже представлена реализация JavaScript указанного выше алгоритма для преобразования любого числа в шестнадцатеричное в строковом представлении. Ее цель — проиллюстрировать указанный выше алгоритм. Однако для серьезной работы с данными гораздо целесообразнее работать с побитовыми операторами .
функция toHex ( d ) { var r знак равно d % 16 ; if ( d - r == 0 ) { return toChar ( r ); } return toHex (( d - r ) / 16 ) + toChar ( r ); } function toChar ( n ) { const Alpha = "0123456789ABCDEF" ; вернуть альфу . charAt ( n ); } 
Также возможно выполнить преобразование, присвоив каждому месту в исходной базе шестнадцатеричное представление его значения места — перед выполнением умножения и сложения для получения окончательного представления. Например, чтобы преобразовать число B3AD в десятичное, можно разбить шестнадцатеричное число на его цифры: B (11 10 ), 3 (3 10 ), A (10 10 ) и D (13 10 ), а затем получить окончательный результат, умножив каждое десятичное представление на 16 p ( p — соответствующая шестнадцатеричная цифра, считая справа налево, начиная с 0). В этом случае мы имеем следующее:
B3AD = (11 × 16 3 ) + (3 × 16 2 ) + (10 × 16 1 ) + (13 × 16 0 )
что составляет 45997 в десятичной системе счисления.
Многие компьютерные системы предоставляют утилиту-калькулятор, способную выполнять преобразования между различными основаниями, часто включая шестнадцатеричные.
В Microsoft Windows утилиту Калькулятор можно установить в режим Программиста, который позволяет выполнять преобразования между основаниями 16 (шестнадцатеричными), 10 (десятичными), 8 ( восьмеричными ) и 2 ( двоичными ), основаниями, наиболее часто используемыми программистами. В режиме Программиста экранная цифровая клавиатура включает шестнадцатеричные цифры от A до F, которые активны при выборе «Hex». Однако в шестнадцатеричном режиме Калькулятор Windows поддерживает только целые числа.
Элементарные операции, такие как деление, могут быть выполнены косвенно путем преобразования в альтернативную систему счисления , например, в широко используемую десятичную систему или двоичную систему, где каждая шестнадцатеричная цифра соответствует четырем двоичным цифрам.
В качестве альтернативы можно также выполнять элементарные операции непосредственно в самой шестнадцатеричной системе — полагаясь на ее таблицы сложения/умножения и соответствующие стандартные алгоритмы, такие как деление в столбик и традиционный алгоритм вычитания.
Как и другие системы счисления, шестнадцатеричная система может использоваться для представления рациональных чисел , хотя повторяющиеся разложения являются обычным явлением, поскольку шестнадцать (10 16 ) имеет только один простой делитель: два.
Для любого основания 0,1 (или «1/10») всегда эквивалентно единице, деленной на представление этого базового значения в его собственной системе счисления. Таким образом, будь то деление одного на два для двоичной системы счисления или деление одного на шестнадцать для шестнадцатеричной системы счисления, обе эти дроби записываются как 0.1. Поскольку основание 16 является полным квадратом (4 2 ), дроби, выраженные в шестнадцатеричной системе счисления, имеют нечетный период гораздо чаще, чем десятичные, и нет циклических чисел (кроме тривиальных однозначных цифр). Повторяющиеся цифры отображаются, когда знаменатель в наименьших членах имеет простой множитель, не найденный в основании; таким образом, при использовании шестнадцатеричной записи все дроби со знаменателями, которые не являются степенью двойки, приводят к бесконечной строке повторяющихся цифр (например, терций и квинтов). Это делает шестнадцатеричную (и двоичную) систему счисления менее удобной, чем десятичную, для представления рациональных чисел, поскольку большая часть лежит за пределами ее диапазона конечного представления.
Все рациональные числа, конечно представимые в шестнадцатеричной системе, также конечно представимы в десятичной, двенадцатеричной и шестидесятеричной : то есть любое шестнадцатеричное число с конечным числом цифр также имеет конечное число цифр, когда выражено в этих других основаниях. И наоборот, только часть тех, которые конечно представимы в последних основаниях, конечно представимы в шестнадцатеричной системе. Например, десятичное 0,1 соответствует бесконечно повторяющемуся представлению 0,1 9 в шестнадцатеричной системе. Однако шестнадцатеричная система более эффективна, чем двенадцатеричная и шестидесятеричная, для представления дробей со степенями двойки в знаменателе. Например, 0,0625 10 (одна шестнадцатая) эквивалентно 0,1 16 , 0,09 12 и 0;3,45 60 .
В таблице ниже приведены разложения некоторых распространенных иррациональных чисел в десятичной и шестнадцатеричной системе счисления.
Степени двойки имеют очень простые расширения в шестнадцатеричной системе. Первые шестнадцать степеней двойки показаны ниже.
Традиционные китайские единицы измерения были шестнадцатеричными. Например, один цзинь (斤) в старой системе равен шестнадцати таэлям . Суаньпань (китайские счеты ) можно использовать для выполнения шестнадцатеричных вычислений, таких как сложение и вычитание. [31]
Как и в случае с двенадцатеричной системой, время от времени предпринимались попытки продвигать шестнадцатеричную систему как предпочтительную систему счисления. Эти попытки часто предлагают определенное произношение и символы для отдельных цифр. [32] Некоторые предложения унифицируют стандартные меры так, чтобы они были кратны 16. [33] [34] Одно из первых таких предложений было выдвинуто Джоном В. Нистромом в «Проекте новой системы арифметики, веса, меры и монет: предложено назвать тональной системой с шестнадцатью в основании» , опубликованном в 1862 году. [35] Нистром среди прочего предложил шестнадцатеричное время , которое подразделяет день на 16, так что в дне 16 «часов» (или «10 тимов », произносится как тонтим ). [36]
Слово hexadecimal впервые зафиксировано в 1952 году. [37] Оно макароническое в том смысле, что сочетает в себе греческое ἕξ (hex) «шесть» с латинским -decimal . Полностью латинская альтернатива sexadecimal (сравните слово sexagesimal для основания 60) старше и, по крайней мере, изредка используется с конца 19 века. [38] Оно все еще используется в 1950-х годах в документации Bendix . Шварцман (1994) утверждает, что использование sexadecimal , возможно, было исключено из-за его предполагаемого сокращения до sex . [39] Многие западные языки с 1960-х годов приняли термины, эквивалентные по построению шестнадцатеричной системе (например, французский hexadécimal , итальянский esadecimale , румынский hexazecimal , сербский хексадецимални и т. д.), но другие ввели термины, которые заменяют родные слова для «шестнадцать» (например, греческий δεκαεξαδικός, исландский sextándakerfi , русский шестнадцатеричной и т. д.)
Терминология и обозначения не были устоявшимися до конца 1960-х годов. В 1969 году Дональд Кнут утверждал, что этимологически правильным термином будет sevenary или, возможно , sedenary , латинский термин, предназначенный для обозначения «сгруппированный по 16» по образцу двоичной , троичной , четверичной и т. д. Согласно аргументу Кнута, правильными терминами для десятичной и восьмеричной арифметики будут денарный и октонарный соответственно. [40] Альфред Б. Тейлор использовал sevenary в своей работе середины 1800-х годов об альтернативных основаниях счисления, хотя он отверг основание 16 из-за его «неудобного количества цифр». [41] [42]
Текущая нотация, использующая буквы от A до F, становится фактическим стандартом с 1966 года, после публикации руководства Fortran IV для IBM System/360 , которое (в отличие от более ранних вариантов Fortran) признает стандарт для ввода шестнадцатеричных констант. [43] Как отмечено выше, альтернативные нотации использовались NEC (1960) и The Pacific Data Systems 1020 (1964). Стандарт, принятый IBM, по-видимому, стал широко распространенным к 1968 году, когда Брюс Алан Мартин в своем письме редактору CACM жалуется , что
С нелепым выбором букв A, B, C, D, E, F в качестве шестнадцатеричных числовых символов, добавляющим и без того неприятные проблемы различения восьмеричных (или шестнадцатеричных) чисел от десятичных чисел (или имен переменных), настало время пересмотреть наши числовые символы. Это следовало сделать до того, как неудачный выбор превратился в фактический стандарт!
Аргумент Мартина состоял в том, что использование цифр от 0 до 9 в недесятеричных числах «подразумевает для нас схему счисления с основанием в десять»: «Почему бы не использовать совершенно новые символы (и названия) для семи или пятнадцати ненулевых цифр, необходимых в восьмеричной или шестнадцатеричной системе. Даже использование букв от A до P было бы улучшением, но совершенно новые символы могли бы отражать двоичную природу системы». [19] Он также утверждал, что «повторное использование букв алфавита для числовых цифр представляет собой гигантский шаг назад по сравнению с изобретением отдельных, неалфавитных глифов для цифр шестнадцать столетий назад» (как цифры брахми , а позднее в индо-арабской системе счисления ), и что последние стандарты ASCII (ASA X3.4-1963 и USAS X3.4-1968) «должны были сохранить шесть позиций кодовой таблицы после десяти десятичных цифр — вместо того, чтобы без необходимости заполнять их знаками пунктуации» (":;<=>?"), которые могли бы быть размещены в другом месте среди 128 доступных позиций.
Base16 (как имя собственное без пробела) может также относиться к двоично-текстовой кодировке, принадлежащей к тому же семейству, что и Base32 , Base58 и Base64 .
В этом случае данные разбиваются на 4-битные последовательности, и каждое значение (от 0 до 15 включительно) кодируется с использованием одного из 16 символов из набора символов ASCII . Хотя могут использоваться любые 16 символов из набора символов ASCII, на практике всегда выбираются цифры ASCII "0"–"9" и буквы "A"–"F" (или строчные "a"–"f"), чтобы соответствовать стандартной письменной нотации для шестнадцатеричных чисел.
Кодирование Base16 имеет ряд преимуществ:
Основными недостатками кодирования Base16 являются:
Поддержка кодировки Base16 повсеместно распространена в современных вычислениях. Она является основой для стандарта W3C для процентного кодирования URL , где символ заменяется знаком процента "%" и его формой в кодировке Base16. Большинство современных языков программирования напрямую включают поддержку форматирования и анализа чисел в кодировке Base16.
{{cite book}}: CS1 maint: location missing publisher (link)"\x1B[0m\x1B[25;1H"определяет последовательность символов Esc [ 0 m Esc [ 2 5; 1 H . Это управляющие последовательности, используемые на терминале ANSI , которые сбрасывают набор символов и цвет, а затем перемещают курсор на строку 25.&префикса восьмеричных значений. (Microsoft BASIC в основном использует &Oпрефикс восьмеричных чисел и &Hпрефикс шестнадцатеричных чисел, но амперсанд сам по себе даёт интерпретацию по умолчанию как восьмеричного префикса.)Эта база используется, поскольку группа из четырех бит может представлять любое из шестнадцати различных чисел (от нуля до пятнадцати). Назначая символ каждой из этих комбинаций, мы приходим к нотации, называемой шестнадцатеричной (обычно "шестнадцатеричной" в разговоре, потому что никто не хочет сокращать "секс"). Символами в шестнадцатеричном языке являются десять десятичных цифр, а на пишущей машинке G-15 — буквы "u", "v", "w", "x", "y" и "z". Это произвольные обозначения; другие компьютеры могут использовать другие символы алфавита для этих последних шести цифр.