Кровообращение (физика)

Линейный интеграл скорости жидкости по замкнутой кривой

Линии поля векторного поля v вокруг границы открытой криволинейной поверхности с бесконечно малым линейным элементом d l вдоль границы и через ее внутреннюю часть с dS — бесконечно малым элементом поверхности и n — единичной нормалью к поверхности. Вверху: Циркуляция — это линейный интеграл v вокруг замкнутого контура C. Спроецируйте v вдоль d l , затем просуммируйте. Здесь v разделяется на компоненты, перпендикулярные (⊥) и параллельные ( ‖ ) d l , параллельные компоненты касательны к замкнутому контуру и вносят вклад в циркуляцию, перпендикулярные компоненты — нет. Внизу: Циркуляция — это также поток завихренности ω = ∇ × v через поверхность, а вихрь v эвристически изображается как винтовая стрелка (не буквальное представление). Обратите внимание , что проекция v вдоль d l и вихрь v могут быть в отрицательном смысле, что уменьшает циркуляцию.

В физике циркуляция — это линейный интеграл векторного поля вокруг замкнутой кривой. В гидродинамике поле — это поле скорости жидкости . В электродинамике это может быть электрическое или магнитное поле.

Впервые Circulation использовали независимо друг от друга Фредерик Ланчестер , Мартин Кутта и Николай Жуковский . ^{[ требуется ссылка ]} Обычно обозначается Γ ( греческая заглавная гамма ).

Определение и свойства

Если V — векторное поле, а d l — вектор, представляющий дифференциальную длину малого элемента определенной кривой, то вклад этой дифференциальной длины в циркуляцию равен dΓ : $${\displaystyle \mathrm {d} \Gamma =\mathbf {V} \cdot \mathrm {d} \mathbf {l} =\left|\mathbf {V} \right|\left|\mathrm {d} \mathbf {l} \right|\cos \theta .}$$

Здесь θ — угол между векторами V и d l .

Циркуляция Γ векторного поля V вокруг замкнутой кривой C представляет собой линейный интеграл : ^{[1] [2]} $${\displaystyle \Gamma =\oint _{C}\mathbf {V} \cdot \mathrm {d} \mathbf {l} .}$$

В консервативном векторном поле этот интеграл равен нулю для каждой замкнутой кривой. Это означает, что линейный интеграл между любыми двумя точками в поле не зависит от выбранного пути. Это также подразумевает, что векторное поле может быть выражено как градиент скалярной функции, который называется потенциалом . ^[2]

Связь с вихреобразованием и завихренностью

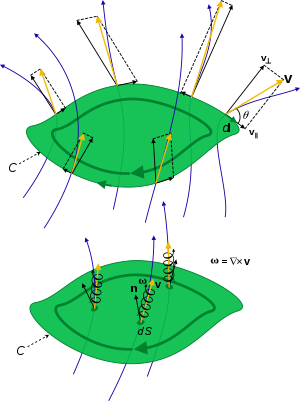
Циркуляция может быть связана с ротором векторного поля V и, более конкретно, с завихренностью, если поле является полем скорости жидкости, $${\displaystyle {\boldsymbol {\omega }}=\nabla \times \mathbf {V} .}$$

По теореме Стокса поток векторов вихря или завихренности через поверхность S равен циркуляции по ее периметру, ^[2] $${\displaystyle \Gamma =\oint _{\partial S}\mathbf {V} \cdot \mathrm {d} \mathbf {l} =\iint _{S}\nabla \times \mathbf {V} \cdot \mathrm {d} \mathbf {S} =\iint _{S}{\boldsymbol {\omega }}\cdot \mathrm {d} \mathbf {S} }$$

Здесь замкнутый путь интегрирования ∂S является границей или периметром открытой поверхности S , чей бесконечно малый элемент нормали d S = n dS ориентирован в соответствии с правилом правой руки . Таким образом, ротор и вихрь являются циркуляцией на единицу площади, взятой вокруг локальной бесконечно малой петли.

В потенциальном течении жидкости с областью завихренности все замкнутые кривые, охватывающие завихренность, имеют одинаковое значение для циркуляции. ^[3]

Использует

Теорема Кутты–Жуковского в гидродинамике

В гидродинамике подъемная сила на единицу пролета (L'), действующая на тело в двумерном поле потока, прямо пропорциональна циркуляции, т.е. ее можно выразить как произведение циркуляции Γ вокруг тела, плотности жидкости и скорости тела относительно свободного потока : ${\displaystyle \rho }$ ${\displaystyle v_{\infty }}$ $${\displaystyle L'=\rho v_{\infty }\Gamma }$$

Это известно как теорема Кутты–Жуковского. ^[4]

Это уравнение применяется вокруг аэродинамических профилей, где циркуляция создается действием аэродинамического профиля ; и вокруг вращающихся объектов, испытывающих эффект Магнуса , где циркуляция вызывается механически. В действии аэродинамического профиля величина циркуляции определяется условием Кутта . ^[4]

Циркуляция на каждой замкнутой кривой вокруг профиля имеет одно и то же значение и связана с подъемной силой, создаваемой каждой единицей длины пролета. При условии, что замкнутая кривая охватывает профиль, выбор кривой произволен. ^[3]

Циркуляция часто используется в вычислительной гидродинамике в качестве промежуточной переменной для расчета сил, действующих на аэродинамический профиль или другое тело.

Основные уравнения электромагнетизма

В электродинамике закон индукции Максвелла-Фарадея можно сформулировать в двух эквивалентных формах: ^[5] ротор электрического поля равен отрицательной скорости изменения магнитного поля, $${\displaystyle \nabla \times \mathbf {E} =-{\frac {\partial \mathbf {B} }{\partial t}}}$$

или что циркуляция электрического поля вокруг петли равна отрицательной скорости изменения потока магнитного поля через любую поверхность, охватываемую петлей, по теореме Стокса $${\displaystyle \oint _{\partial S}\mathbf {E} \cdot \mathrm {d} \mathbf {l} =\iint _{S}\nabla \times \mathbf {E} \cdot \mathrm {d} \mathbf {S} =-{\frac {\mathrm {d} }{\mathrm {d} t}}\int _{S}\mathbf {B} \cdot \mathrm {d} \mathbf {S} .}$$

Циркуляция статического магнитного поля , согласно закону Ампера , пропорциональна полному току, заключенному в контуре. $${\displaystyle \oint _{\partial S}\mathbf {B} \cdot \mathrm {d} \mathbf {l} =\mu _{0}\iint _{S}\mathbf {J} \cdot \mathrm {d} \mathbf {S} =\mu _{0}I_{\text{enc}}.}$$

Для систем с электрическими полями, которые меняются со временем, закон необходимо модифицировать, включив в него член, известный как поправка Максвелла.

Смотрите также

• Уравнения Максвелла
• Закон Био–Савара в аэродинамике
• Теорема Кельвина о циркуляции

Ссылки

1. Роберт В. Фокс; Алан Т. Макдональд; Филип Дж. Притчард (2003). Введение в механику жидкости (6-е изд.). Wiley . ISBN 978-0-471-20231-8.
2. "Лекции Фейнмана по физике, том II, гл. 3: Векторные интегральные исчисления". feynmanlectures.caltech.edu . Получено 2020-11-02 .
3. Андерсон, Джон Д. (1984), Основы аэродинамики , раздел 3.16. McGraw-Hill. ISBN 0-07-001656-9 
4. А. М. Кете; Дж. Д. Шетцер (1959). Основы аэродинамики (2-е изд.). Джон Уайли и сыновья . §4.11. ISBN 978-0-471-50952-3.
5. "Лекции Фейнмана по физике. Том II. Гл. 17: Законы индукции". feynmanlectures.caltech.edu . Получено 2020-11-02 .