Коэффициент каппа Коэна ( κ , строчная греческая каппа ) — это статистика , которая используется для измерения межэкспертной надежности (а также внутриэкспертной надежности ) для качественных (категориальных) элементов. [1] Обычно считается, что это более надежная мера, чем простой расчет процента согласия, поскольку κ учитывает возможность случайного согласия. Вокруг каппы Коэна существуют разногласия из-за сложности интерпретации индексов согласия. Некоторые исследователи предполагают, что концептуально проще оценить несогласие между элементами. [2]
Первое упоминание о каппа-подобной статистике приписывается Гальтону в 1892 году. [3] [4]
Основополагающая статья, представляющая каппу как новую технику, была опубликована Джейкобом Коэном в журнале Educational and Psychological Measurement в 1960 году. [5]
Каппа Коэна измеряет согласие между двумя оценщиками, каждый из которых классифицирует N элементов по C взаимоисключающим категориям. Определение :
где p o — относительное наблюдаемое согласие среди оценщиков, а p e — гипотетическая вероятность случайного согласия, использующая наблюдаемые данные для расчета вероятностей случайного выбора каждой категории каждым наблюдателем. Если оценщики полностью согласны, то . Если нет согласия среди оценщиков, кроме того, которое можно было бы ожидать случайно (как указано p e ), . Статистика может быть отрицательной, [6] что может произойти случайно, если нет никакой связи между оценками двух оценщиков, или это может отражать реальную тенденцию оценщиков давать разные оценки.
Для k категорий, N наблюдений для категоризации и количество раз, когда оценщик i предсказал категорию k :
Это вытекает из следующей конструкции:
Где — предполагаемая вероятность того, что и оценщик 1, и оценщик 2 классифицируют один и тот же элемент как k, а — предполагаемая вероятность того, что оценщик 1 классифицирует элемент как k (и аналогично для оценщика 2). Соотношение основано на использовании предположения, что рейтинги двух оценщиков независимы . Член оценивается с использованием количества элементов, классифицированных как k оценщиком 1 ( ), деленного на общее количество элементов для классификации ( ): (и аналогично для оценщика 2).
В традиционной матрице путаницы 2 × 2 , используемой в машинном обучении и статистике для оценки бинарных классификаций , формула Каппа Коэна может быть записана как: [7]
где TP — истинные положительные результаты, FP — ложные положительные результаты, TN — истинные отрицательные результаты, а FN — ложные отрицательные результаты. В этом случае Каппа Коэна эквивалентна показателю мастерства Хайдке , известному в метеорологии . [8] Мера была впервые введена Мириком Хаскеллом Дулитлом в 1888 году. [9]
Предположим, что вы анализируете данные, связанные с группой из 50 человек, подающих заявку на грант. Каждое предложение о гранте читали два читателя, и каждый читатель либо говорил «Да», либо «Нет» на предложение. Предположим, что данные о подсчете несогласия были следующими, где A и B — читатели, данные на главной диагонали матрицы (a и d) подсчитывают количество согласий, а данные вне диагонали (b и c) подсчитывают количество несогласий:
например
Наблюдаемое пропорциональное согласие:
Для расчета p e (вероятности случайного согласия) заметим, что:
Таким образом, ожидаемая вероятность того, что оба ответят «да» наугад, составляет:
Сходным образом:
Общая вероятность случайного согласия — это вероятность того, что они согласились либо с ответом «Да», либо с ответом «Нет», то есть:
Итак, теперь, применяя нашу формулу для Каппы Коэна, мы получаем:
Случай, который иногда считается проблемой с каппой Коэна, возникает при сравнении каппы, рассчитанной для двух пар оценщиков, когда два оценщика в каждой паре имеют одинаковое процентное согласие, но одна пара дает схожее количество оценок в каждом классе, в то время как другая пара дает совершенно разное количество оценок в каждом классе. [10] (В приведенных ниже случаях уведомление B имеет 70 «да» и 30 «нет» в первом случае, но эти числа меняются местами во втором.) Например, в следующих двух случаях наблюдается равное согласие между A и B (60 из 100 в обоих случаях) с точки зрения согласия в каждом классе, поэтому мы ожидаем, что относительные значения каппы Коэна будут отражать это. Однако, вычисляя каппу Коэна для каждого:
мы обнаруживаем, что во втором случае наблюдается большее сходство между A и B по сравнению с первым. Это происходит потому, что, хотя процентное согласие одинаково, процентное согласие, которое произошло бы «случайно», значительно выше в первом случае (0,54 по сравнению с 0,46).
Значение P для каппы сообщается редко, вероятно, потому, что даже относительно низкие значения каппы могут, тем не менее, значительно отличаться от нуля, но не настолько, чтобы удовлетворить исследователей. [11] : 66 Тем не менее, его стандартная ошибка была описана [12] и вычисляется различными компьютерными программами. [13]
Доверительные интервалы для Каппы могут быть построены для ожидаемых значений Каппы, если бы у нас было бесконечное количество проверенных элементов, с использованием следующей формулы: [1]
Где находится стандартный нормальный процентиль, когда , и
Это вычисляется путем игнорирования того, что p e оценивается на основе данных, и путем рассмотрения p o как оценочной вероятности биномиального распределения с использованием асимптотической нормальности (т. е.: предполагая, что количество элементов велико и что p o не близко ни к 0, ни к 1). (и CI в целом) также может быть оценен с использованием методов бутстрепа .

Если статистическая значимость не является полезным руководством, какая величина каппы отражает адекватное согласие? Руководящие принципы были бы полезны, но факторы, отличные от согласия, могут влиять на ее величину, что делает интерпретацию данной величины проблематичной. Как отметили Сим и Райт, двумя важными факторами являются распространенность (равновероятны ли коды или их вероятности различаются) и смещение (являются ли предельные вероятности для двух наблюдателей одинаковыми или разными). При прочих равных условиях каппы выше, когда коды равновероятны. С другой стороны, каппы выше, когда коды распределены асимметрично двумя наблюдателями. В отличие от вариаций вероятности, эффект смещения больше, когда каппа мала, чем когда она велика. [14] : 261–262
Другим фактором является количество кодов. По мере увеличения количества кодов каппы становятся выше. На основе исследования симуляции Бейкман и его коллеги пришли к выводу, что для наблюдателей, допускающих ошибки, значения каппы были ниже, когда кодов было меньше. И, в соответствии с утверждением Сима и Райтса относительно распространенности, каппы были выше, когда коды были примерно равновероятными. Таким образом, Бейкман и др. пришли к выводу, что «ни одно значение каппы не может считаться универсально приемлемым». [15] : 357 Они также предоставляют компьютерную программу, которая позволяет пользователям вычислять значения каппы, указывая количество кодов, их вероятность и точность наблюдателя. Например, при равновероятных кодах и наблюдателях, которые точны на 85%, значения каппы составляют 0,49, 0,60, 0,66 и 0,69, когда количество кодов составляет 2, 3, 5 и 10 соответственно.
Тем не менее, в литературе появились рекомендации по величине. Возможно, первыми были Лэндис и Кох [16] , которые охарактеризовали значения < 0 как указывающие на отсутствие согласия, а 0–0,20 как небольшое, 0,21–0,40 как удовлетворительное, 0,41–0,60 как умеренное, 0,61–0,80 как существенное и 0,81–1 как почти идеальное согласие. Однако этот набор рекомендаций никоим образом не является общепринятым; Лэндис и Кох не предоставили никаких доказательств в его поддержку, вместо этого основываясь на личном мнении. Было отмечено, что эти рекомендации могут быть скорее вредными, чем полезными. [17] Флейсс [18] : 218 столь же произвольных рекомендаций характеризуют каппы более 0,75 как отличные, от 0,40 до 0,75 как удовлетворительные или хорошие, а ниже 0,40 как плохие.
Каппа принимает свое теоретическое максимальное значение 1 только тогда, когда оба наблюдателя распределяют коды одинаково, то есть когда соответствующие суммы строк и столбцов идентичны. Все, что меньше, меньше идеального согласия. Тем не менее, максимальное значение, которого может достичь каппа при неравных распределениях, помогает интерпретировать фактически полученное значение каппы. Уравнение для максимума κ имеет вид: [19]
где , как обычно, ,
k = количество кодов, — вероятности строк, а — вероятности столбцов.
Каппа — это индекс, который учитывает наблюдаемое согласие относительно базового согласия. Однако исследователи должны тщательно рассмотреть, является ли базовое согласие Каппы релевантным для конкретного исследовательского вопроса. Базовое согласие Каппы часто описывается как согласие, обусловленное случайностью, что верно лишь отчасти. Базовое согласие Каппы — это согласие, которое можно было бы ожидать из-за случайного распределения, учитывая количества, указанные в предельных суммах таблицы сопряженности квадратов. Таким образом, κ = 0, когда наблюдаемое распределение, по-видимому, случайно, независимо от количественного несоответствия, ограниченного предельными суммами. Однако для многих приложений исследователи должны быть больше заинтересованы в количественном несоответствии в предельных суммах, чем в несоответствии распределения, описанном дополнительной информацией на диагонали таблицы сопряженности квадратов. Таким образом, для многих приложений базовое согласие Каппы больше отвлекает, чем проясняет. Рассмотрим следующий пример:
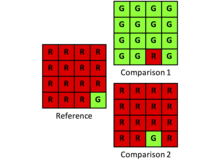
Пропорция несогласия составляет 14/16 или 0,875. Несогласие обусловлено количеством, поскольку распределение оптимально. κ составляет 0,01.
Пропорция несогласованности составляет 2/16 или 0,125. Несогласованность обусловлена распределением, поскольку количества идентичны. Каппа составляет −0,07.
Здесь сообщение о разногласии по количеству и распределению является информативным, в то время как Каппа скрывает информацию. Кроме того, Каппа вносит некоторые проблемы в расчеты и интерпретацию, поскольку Каппа является отношением. Отношение Каппы может возвращать неопределенное значение из-за нуля в знаменателе. Кроме того, отношение не раскрывает ни числитель, ни знаменатель. Для исследователей более информативно сообщать о разногласии по двум компонентам, количеству и распределению. Эти два компонента описывают связь между категориями более четко, чем одна сводная статистика. Когда целью является точность прогнозирования, исследователям легче начать думать о способах улучшения прогноза, используя два компонента количества и распределения, а не одно отношение Каппы. [2]
Некоторые исследователи выразили обеспокоенность по поводу тенденции κ принимать частоты наблюдаемых категорий как данность, что может сделать ее ненадежной для измерения согласия в таких ситуациях, как диагностика редких заболеваний. В этих ситуациях κ имеет тенденцию недооценивать согласие по редкой категории. [20] По этой причине κ считается чрезмерно консервативной мерой согласия. [21] Другие [22] [ требуется цитирование ] оспаривают утверждение, что каппа «учитывает» случайное согласие. Чтобы сделать это эффективно, потребуется явная модель того, как случайность влияет на решения оценщиков. Так называемая корректировка вероятности статистики каппы предполагает, что, когда нет полной уверенности, оценщики просто угадывают — очень нереалистичный сценарий. Более того, некоторые работы [23] показали, как статистика каппы может привести к неверному выводу для несбалансированных данных.
Подобная статистика, называемая pi , была предложена Скоттом (1955). Каппа Коэна и pi Скотта различаются с точки зрения того, как рассчитывается p e .
Обратите внимание, что каппа Коэна измеряет согласие только между двумя оценщиками. Для аналогичной меры согласия ( каппа Флейсса ), используемой, когда есть более двух оценщиков, см. Fleiss (1971). Каппа Флейсса, однако, является многооценочным обобщением статистики pi Скотта , а не каппы Коэна. Каппа также используется для сравнения производительности в машинном обучении , но направленная версия, известная как статистика информированности или J Юдена, как утверждается, более подходит для контролируемого обучения. [24]
Взвешенная каппа позволяет взвешивать разногласия по-разному [25] и особенно полезна, когда коды упорядочены. [11] : 66 Вовлечены три матрицы: матрица наблюдаемых оценок, матрица ожидаемых оценок, основанная на случайном согласии, и матрица весов. Ячейки матрицы весов, расположенные по диагонали (с верхнего левого угла в нижний правый), представляют согласие и, таким образом, содержат нули. Ячейки вне диагонали содержат веса, указывающие на серьезность этого разногласия. Часто ячейки, одна вне диагонали, имеют вес 1, две вне диагонали — 2 и т. д.
Уравнение для взвешенного κ имеет вид:
где k = число кодов, а , , и являются элементами в весовой, наблюдаемой и ожидаемой матрицах соответственно. Когда диагональные ячейки содержат веса 0, а все недиагональные ячейки имеют веса 1, эта формула дает то же значение каппы, что и расчет, приведенный выше.