Головоломка на равновесие

Логическая головоломка

Головоломка с балансом или головоломка со взвешиванием — это логическая головоломка, в которой нужно уравновешивать предметы (часто монеты), чтобы определить, какой из них имеет иную ценность, используя весы ограниченное количество раз. Они отличаются от головоломок, в которых предметам присваивается вес, тем, что имеет значение только относительная масса этих предметов.

Например, при обнаружении разной монеты за три взвешивания (n = 3) максимальное количество монет, которые можно проанализировать, составляет ⁠3 ³ − 1/2⁠ = 13. Обратите внимание, что при 3 весах и 13 монетах не всегда можно определить идентичность последней монеты (тяжелее она или легче остальных), а только то, что монета отличается. В общем, при n весах вы можете определить идентичность монеты, если у вас есть ⁠3 ^н − 1/2⁠ - 1 или менее монет. В случае n = 3 вы действительно можете обнаружить идентичность отличающейся монеты из 12 монет.

Эта версия задачи с двенадцатью монетами появилась в печати еще в 1945 году ^{[2] [3]} , и Гай и Новаковски объясняют, что она «была популярна по обе стороны Атлантики во время Второй мировой войны; даже предлагалось сбросить ее над Германией в попытке саботировать ее военные усилия». ^[3]

Задача о девяти монетах

Решение головоломки с весами для 9 монет за 2 взвешивания, где лишняя монета легче остальных – если лишняя монета тяжелее остальных, то верхние две ветви в каждом решении о взвешивании меняются местами

Известный пример имеет до девяти предметов, скажем, монет (или шариков), которые одинаковы по весу, за исключением одного, который легче остальных — фальшивки (oddball). Разница заметна только при взвешивании их на весах — но взвесить можно только сами монеты. Как можно изолировать фальшивую монету всего двумя взвешиваниями?

Решение

Чтобы найти решение, сначала рассмотрим максимальное количество предметов, из которых можно найти более легкий всего за одно взвешивание. Максимально возможное количество — три. Чтобы найти более легкий, мы можем сравнить любые две монеты, исключив третью. Если две монеты весят одинаково, то более легкая монета должна быть одной из тех, которых нет на весах. В противном случае это та, которую весы показали как более легкую.

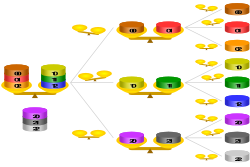
Теперь представьте девять монет в трех стопках по три монеты в каждой. За один ход мы можем определить, какая из трех стопок легче (т. е. та, в которой находится более легкая монета). Затем требуется всего один ход, чтобы определить легкую монету в этой более легкой стопке. Таким образом, за два взвешивания мы можем найти одну легкую монету из набора 3 × 3 = 9 .

Другими словами, для того, чтобы найти лишнюю легкую монету среди 27 монет, потребуется всего три взвешивания, а для того, чтобы найти ее среди 81 монеты, потребуется четыре взвешивания.

Задача о двенадцати монетах

В более сложной версии двенадцать монет, одиннадцать из двенадцати из которых идентичны. Если одна отличается, мы не знаем, тяжелее она или легче остальных. На этот раз весы можно использовать три раза, чтобы определить, есть ли уникальная монета, и если есть, то изолировать ее и определить ее вес относительно других. (Эта головоломка и ее решение впервые появились в статье в 1945 году. ^[4] ) У задачи есть более простой вариант с тремя монетами за два взвешивания и более сложный вариант с 39 монетами за четыре взвешивания.

Решение

Эта проблема имеет более одного решения. Одно из них легко масштабируется до большего количества монет с помощью нумерации с основанием три: маркируя каждую монету различным числом из трех цифр в основании три и размещая на n -м взвешивании все монеты, которые маркированы n -й цифрой, идентичной маркировке пластины (с тремя пластинами, по одной с каждой стороны весов с маркировкой 0 и 2, и одной вне весов с маркировкой 1). Другие пошаговые процедуры аналогичны следующим. Для этой проблемы это менее просто, и второе и третье взвешивания зависят от того, что произошло ранее, хотя это не обязательно так (см. ниже).

• Четыре монеты кладутся на каждую сторону. Есть два варианта:

1. Одна сторона тяжелее другой. Если это так, уберите три монеты с более тяжелой стороны, переложите три монеты с более легкой стороны на более тяжелую и положите три монеты, которые не были взвешены в первый раз, на более легкую сторону. (Запомните, какие монеты какие.) Есть три возможности:

1.a) Та же сторона, которая была тяжелее в первый раз, все еще тяжелее. Это означает, что либо монета, которая осталась там, тяжелее, либо монета, которая осталась на более легкой стороне, легче. Уравновешивание одной из этих монет с одной из десяти других показывает, какая из них верна, тем самым решая головоломку.

1.b) Сторона, которая была тяжелее в первый раз, легче во второй раз. Это означает, что одна из трех монет, перешедших с более легкой стороны на более тяжелую, является легкой монетой. Для третьей попытки взвесьте две из этих монет друг против друга: если одна легче, то это уникальная монета; если они уравновешены, то третья монета является легкой.

1.c) Обе стороны ровные. Это значит, что одна из трех монет, которая была снята с более тяжелой стороны, является тяжелой монетой. Для третьей попытки взвесьте две из этих монет друг против друга: если одна тяжелее, то это уникальная монета; если они уравновешены, то третья монета является тяжелой.

2. Обе стороны равны. Если это так, то все восемь монет одинаковы и их можно отложить. Возьмите четыре оставшиеся монеты и положите три на одну сторону весов. Положите 3 из 8 одинаковых монет на другую сторону. Есть три возможности:

2.a) Три оставшиеся монеты легче. В этом случае вы теперь знаете, что одна из этих трех монет лишняя и она легче. Возьмите две из этих трех монет и взвесьте их друг с другом. Если весы наклонятся, то более легкая монета лишняя. Если две монеты уравновесятся, то третья монета, не лежащая на весах, лишняя и она легче.

2.b) Три оставшиеся монеты тяжелее. В этом случае вы теперь знаете, что одна из этих трех монет лишняя и что она тяжелее. Возьмите две из этих трех монет и взвесьте их друг с другом. Если весы наклонятся, то более тяжелая монета лишняя. Если две монеты уравновесятся, то третья монета, не лежащая на весах, лишняя и она тяжелее.

2.c) Три оставшиеся монеты уравновешивают друг друга. В этом случае вам просто нужно взвесить оставшуюся монету против любой из 11 других монет, и это скажет вам, тяжелее она, легче или такая же.

Вариации

Имея в наличии 13 монет, среди которых известно, что 1 из 13 отличается (по массе) от остальных, легко определить, какая это монета, с помощью весов и 3 тестов следующим образом:

1) Разделите монеты на 2 группы по 4 монеты и третью группу из оставшихся 5 монет.

2) Тест 1. Сравните две группы по 4 монеты друг с другом:

а. Если монеты уравновешены, то лишняя монета входит в совокупность из 5 и переходим к тесту 2а.

б) Лишняя монета находится среди 8 монет, действуйте так же, как в задаче с 12 монетами.

3) Тест 2а. Тест 3 монет из группы из 5 монет против любых 3 монет из группы из 8 монет:

а. Если 3 монеты уравновешены, то лишняя монета находится среди оставшихся 2 монет. Протестируйте одну из 2 монет против любой другой монеты; если они уравновешены, лишняя монета — это последняя непроверенная монета, если они не уравновешены, лишняя монета — это текущая тестовая монета.

б. Если 3 монеты не уравновешиваются, то лишняя монета из этой популяции из 3 монет. Обратите внимание на направление колебания баланса (вверх означает, что лишняя монета легкая, вниз означает, что она тяжелая). Уберите одну из 3 монет, переместите другую на другую сторону весов (уберите все остальные монеты с баланса). Если баланс выровняется, то лишняя монета — это монета, которую убрали. Если баланс меняет направление, то лишняя монета — это та, которую переместили на другую сторону, в противном случае лишняя монета — это монета, которая осталась на месте.

С эталонной монетой

Если есть одна подлинная монета для сравнения, то подозрительных монет может быть 13. Пронумеруйте монеты от 1 до 13, а подлинную монету присвойте номеру 0 и выполните эти взвешивания в любом порядке:

• 0, 1, 4, 5, 6 против 7, 10, 11, 12, 13
• 0, 2, 4, 10, 11 против 5, 8, 9, 12, 13
• 0, 3, 8, 10, 12 против 6, 7, 9, 11, 13

Если весы не сбалансированы только один раз, то это должна быть одна из монет 1, 2, 3, которые появляются только в одном взвешивании. Если равновесия нет никогда, то это должна быть одна из монет 10–13, которые появляются во всех взвешиваниях. Выбор одной фальшивой монеты, соответствующей каждому из 27 результатов, всегда возможен (13 монет, одна из которых слишком тяжелая или слишком легкая, — это 26 возможностей), за исключением случаев, когда все взвешивания сбалансированы, в этом случае фальшивой монеты нет (или ее вес правильный). Если монеты 0 и 13 удалить из этих взвешиваний, они дают одно общее решение задачи с 12 монетами.

Если две монеты фальшивые, эта процедура, в общем случае, не выбирает ни одну из них, а выбирает какую-то подлинную монету. Например, если обе монеты 1 и 2 фальшивые, то либо монета 4, либо монета 5 выбраны неправильно.

Без референтной монеты

В расслабленной вариации этой головоломки нужно только найти фальшивую монету, не обязательно имея возможность определить ее вес относительно других. В этом случае, очевидно, любое решение, которое ранее взвешивало каждую монету в какой-то момент, может быть адаптировано для обработки одной дополнительной монеты. Эта монета никогда не кладется на весы, но если все взвешивания уравновешены, она выбирается как фальшивая монета. Сделать что-то лучше невозможно, поскольку любой монете, которая в какой-то момент кладется на весы и выбирается как фальшивая монета, всегда может быть назначен вес относительно других.

Метод, который взвешивает одни и те же наборы монет независимо от результатов, позволяет либо

1. (среди 12 монет A–L) сделайте вывод, все ли они весят одинаково, или найдите лишнюю монету и скажите, легче она или тяжелее, или
2. (среди 13 монет A–M) найдите лишнюю монету и с вероятностью 12/13 определите, легче она или тяжелее (с вероятностью 1/13 определите, что она другая).

Три возможных результата каждого взвешивания можно обозначить как "\" для левой стороны, которая легче, "/" для правой стороны, которая легче, и "–" для обеих сторон, имеющих одинаковый вес. Символы для взвешиваний перечислены в последовательности. Например, "//–" означает, что правая сторона легче при первом и втором взвешивании, и обе стороны весят одинаково при третьем взвешивании. Три взвешивания дают следующие 3 ³ = 27 результатов. За исключением "–––", наборы разделены таким образом, что каждый набор справа имеет "/", а набор слева имеет "\", и наоборот:

/// \\\\// /\\/\/ \/\//\ \\/\/– /\––\/ –/\/–\ \–/\\– //––\\ –//\–\ /–//–– \–––/– –\–––/ ––\–––

Поскольку каждое взвешивание дает осмысленный результат только тогда, когда количество монет на левой стороне равно количеству на правой стороне, мы игнорируем первую строку, так что каждый столбец имеет одинаковое количество символов "\" и "/" (по четыре каждого). Строки помечены, порядок монет не имеет значения:

\// Легкий /\\ Тяжелый/\/ B легкий \/\ B тяжелый//\ C легкий \\/ C тяжелый\/– D легкий /\– D тяжелый–\/ E легкий –/\ E тяжелый/–\ Ф лёгкий \–/ Ф тяжёлый\\– G легкий //– G тяжелый–\\ H легкий –// H тяжелый\–\ Я лёгкий /–/ Я тяжёлый/–– J легкий \–– J тяжелый–/– К легкий –\– К тяжелый––/ Л легкий ––\ Л тяжелый––– M либо легче, либо тяжелее (13-монетный корпус), или все монеты весят одинаково (шкала на 12 монет)

Используя приведенную выше схему результатов, можно определить состав монет для каждого взвешивания; например, набор «\/– D легкая» подразумевает, что монета D должна находиться на левой стороне при первом взвешивании (чтобы эта сторона была легче), на правой стороне при втором взвешивании и неиспользованной при третьем:

1-е взвешивание: левая сторона: ADGI, правая сторона: BCFJ2-е взвешивание: левая сторона: BEGH, правая сторона: ACDK3-е взвешивание: левая сторона: CFHI, правая сторона: ABEL

Затем результаты считываются с таблицы. Например, если правая сторона легче в первых двух взвешиваниях, а обе стороны весят одинаково в третьем, соответствующий код «//– G тяжелая» означает, что монета G лишняя, и она тяжелее остальных. ^[5]

Обобщение на несколько масштабов

В другом обобщении этой проблемы у нас есть две весы, которые можно использовать параллельно. Например, если вы знаете, что ровно одна монета отличается, но не знаете, тяжелее она или легче обычной монеты, то в раундах вы можете решить задачу с максимальным количеством монет. ^[6] ${\displaystyle n}$ ${\displaystyle (5^{n}-5)/2}$

Обобщение на несколько неизвестных монет

Обобщение этой проблемы описано в работе Чуднова. ^[7]

Пусть будет -мерным евклидовым пространством и будет скалярным произведением векторов и из Для векторов и подмножеств операции и определяются соответственно как  ; , , Через будем обозначать дискретный [−1; 1]-куб в ; т. е. множество всех последовательностей длины над алфавитом Множество представляет собой дискретный шар радиуса (в метрике Хэмминга ) с центром в точке Относительные веса объектов задаются вектором , определяющим конфигурации весов объектов: й объект имеет стандартный вес, если вес й объекта больше (меньше) на постоянную (неизвестную) величину, если (соответственно, ). Вектор характеризует типы объектов: стандартный тип, нестандартный тип (т. е. конфигурации типов), и он не содержит информации об относительных весах нестандартных объектов. ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle n}$ ${\displaystyle [\mathrm {e} ^{1},\mathrm {e} ^{2}]}$ ${\displaystyle \mathrm {e} ^{1}}$ ${\displaystyle \mathrm {e} ^{2}}$ ${\displaystyle \mathbb {R} ^{n}.}$ ${\displaystyle \mathrm {e} =(e_{1},\dots ,e_{n})\in \mathbb {R} ^{n}}$ ${\displaystyle E=\{\mathrm {e} ^{j}\}\subseteq \mathbb {R} ^{n},}$ ${\displaystyle (\cdot )^{*}}$ ${\displaystyle (\cdot )^{+}}$ ${\displaystyle \mathrm {e} ^{*}=(sign(e_{i}))_{i}}$ ${\displaystyle E^{*}=\{(\mathrm {e} ^{j})^{*}\}}$ ${\displaystyle \mathrm {e} ^{+}=(|sign(e_{i})|)_{i}}$ ${\displaystyle E^{+}=\{(\mathrm {e} ^{j})^{+}\}.}$ ${\displaystyle I^{n}}$ ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle n}$ ${\displaystyle I=\{-1,0,1\}}$ ${\displaystyle I_{t}^{n}=\{\mathrm {x} \in I^{n}|w(\mathrm {x} )\leq t\}\subseteq I^{n}}$ ${\displaystyle t}$ ${\displaystyle w()}$ ${\displaystyle \mathrm {0} .}$ ${\displaystyle n}$ ${\displaystyle \mathrm {x} =(x_{1},\dots ,x_{n})\in I^{n},}$ ${\displaystyle i}$ ${\displaystyle x_{i}=0;}$ ${\displaystyle i}$ ${\displaystyle x_{i}=1}$ ${\displaystyle x_{i}=-1}$ ${\displaystyle \mathrm {x} ^{+}}$

Взвешивание (проверка) задается вектором результат взвешивания для ситуации равен Взвешивание, заданное вектором, имеет следующую интерпретацию: для данной проверки во взвешивании участвует -й объект, если ; он кладется на левую чашу весов, если и кладется на правую чашу, если Для каждого взвешивания обе чаши должны содержать одинаковое количество объектов: если на какой-то чаше весов количество объектов меньше положенного, то на нее подаются эталонные объекты. Результат взвешивания описывает следующие случаи: весы , если , левая чаша перевешивает правую, если , и правая чаша перевешивает левую, если Неполнота исходной информации о распределении весов группы объектов характеризуется множеством допустимых распределений весов объектов , которое также называется множеством допустимых ситуаций, элементы из называются допустимыми ситуациями. ${\displaystyle \mathrm {h} \in I^{n};}$ ${\displaystyle \mathrm {x} \in I^{n}}$ ${\displaystyle s(\mathrm {x} ;\mathrm {h} )=sign([\mathrm {x} ;\mathrm {h} ]).}$ ${\displaystyle \mathrm {h} =(h_{1},\dots ,h_{n})}$ ${\displaystyle i}$ ${\displaystyle h_{i}\neq 0}$ ${\displaystyle h_{i}<0}$ ${\displaystyle h_{i}>0.}$ ${\displaystyle \mathrm {h} }$ ${\displaystyle r(\mathrm {h} )=[\mathrm {h} ;1,\dots ,1]}$ ${\displaystyle s(\mathrm {x} ;\mathrm {h} )}$ ${\displaystyle s(\mathrm {x} ;\mathrm {h} )=0}$ ${\displaystyle s(\mathrm {x} ;\mathrm {h} )=-1}$ ${\displaystyle s(\mathrm {x} ;\mathrm {h} )=1.}$ ${\displaystyle Z\subseteq I^{n},}$ ${\displaystyle z\in Z}$

Каждое взвешивание индуцирует разбиение множества плоскостью ( гиперплоскостью ) на три части и определяет соответствующее разбиение множества , где ${\displaystyle \mathrm {h} }$ ${\displaystyle I^{n}}$ ${\displaystyle [\mathrm {x} ;\mathrm {h} ]=0}$ ${\displaystyle W(s|I^{n};\mathrm {h} )=\{\mathrm {x} \in I^{n}|s(\mathrm {x} ;\mathrm {h} )=s\}}$ ${\displaystyle s\in I,}$ ${\displaystyle Z=W(0|Z,\mathrm {h} )+W(1|Z,\mathrm {h} )+W(-1|Z,\mathrm {h} ),}$ ${\displaystyle W(s|Z,\mathrm {h} )=W(s|I^{n},\mathrm {h} )\cap Z.}$

Определение 1. Алгоритм взвешивания (ВА) длины — это последовательность , где — функция, определяющая проверку на каждом -м шаге алгоритма по результатам взвешиваний на предыдущих шагах ( — заданная начальная проверка). ${\displaystyle {\mathcal {A}}}$ ${\displaystyle m}$ ${\displaystyle {\mathcal {A}}=<\mathrm {A} _{1},\dots ,\mathrm {A} _{m}>,}$ ${\displaystyle \mathrm {A} _{j}:I^{j-1}\to I^{n}}$ ${\displaystyle \mathrm {h} ^{j}=\mathrm {A} _{j}(s^{j-1});\mathrm {h} ^{j}\in I^{n},}$ ${\displaystyle j}$ ${\displaystyle j=1,2,\dots ,m,}$ ${\displaystyle \mathrm {s} ^{j-1}=(s_{1},\dots ,s_{j-1})\in I^{j-1}}$ ${\displaystyle \mathrm {h} ^{1}=\mathrm {A} _{1}()}$

Пусть будет множеством всех -синдромов, а будет множеством ситуаций с тем же синдромом ; т.е. ; ${\displaystyle S(Z,{\mathcal {A}})}$ ${\displaystyle (Z,{\mathcal {A}})}$ ${\displaystyle W(s|{\mathcal {A}})\subseteq I}$ ${\displaystyle s}$ ${\displaystyle W(s|{\mathcal {A}})=\{\mathrm {z} \in I^{m}|s(z|{\mathcal {A}})=s\}}$ ${\displaystyle W(s|Z;{\mathcal {A}})=W(s|{\mathcal {A}})\cap Z.}$

Определение 2. Говорят, что WA : а) определяет ситуации в наборе , если условие выполняется для всех б) определяет типы объектов в наборе , если условие выполняется для всех ${\displaystyle {\mathcal {A}}}$ ${\displaystyle Z}$ ${\displaystyle |W(s|Z,{\mathcal {A}})|=1}$ ${\displaystyle s\in S(Z{\mathcal {A}});}$ ${\displaystyle Z}$ ${\displaystyle |W^{+}(s|Z{\mathcal {A}})|=1}$ ${\displaystyle s\in S(Z{\mathcal {A}}).}$

^{В [7]} доказано , что для так называемых подходящих множеств алгоритм идентификации типов идентифицирует также ситуации в ${\displaystyle Z}$ ${\displaystyle Z.}$

^{В качестве примера в [7]} построены совершенные динамические (двухкаскадные) алгоритмы с параметрами , соответствующими параметрам совершенного троичного кода Голея (кода Виртакаллио-Голея). При этом установлено, что статического WA (т.е. кода с весами) с такими же параметрами не существует. ${\displaystyle n=11,m=5,t=2}$

Каждый из этих алгоритмов с помощью 5 взвешиваний находит среди 11 монет до двух фальшивых монет, которые могут быть тяжелее или легче настоящих монет на одинаковую величину. В этом случае область неопределенности (множество допустимых ситуаций) содержит ситуации, т.е. построенная WA лежит на границе Хэмминга для и в этом смысле является идеальной. ${\displaystyle 1+2C_{11}^{1}+2^{2}C_{11}^{2}=3^{5}}$ ${\displaystyle t=2}$

На сегодняшний день неизвестно, существуют ли другие совершенные WA, которые идентифицируют ситуации в для некоторых значений . Более того, неизвестно, существуют ли для некоторых решения уравнения (соответствующего границе Хэмминга для троичных кодов), что, очевидно, необходимо для существования совершенного WA. Известно лишь, что для совершенных WA не существует, а для это уравнение имеет единственное нетривиальное решение , которое определяет параметры построенного совершенного WA. ${\displaystyle I_{t}^{n}}$ ${\displaystyle n,t}$ ${\displaystyle t>2}$ ${\displaystyle \sum _{i=0}^{t}2^{i}C_{n}^{i}=3^{m}}$ ${\displaystyle t=1}$ ${\displaystyle t=2}$ ${\displaystyle n=11,m=5}$

Ссылки

1. Smith, CAB (февраль 1947). «Проблема фальшивой монеты». Mathematical Gazette . 31 (293): 31–39. doi :10.2307/3608991. JSTOR  3608991.
2. Гроссман, Говард Д. (сентябрь–декабрь 1945 г.). «Проблема двенадцати монет». Scripta Mathematica . 11 (3–4): 360–361.
3. Гай, Ричард; Новаковски, Ричард (февраль 1995 г.). «Проблемы взвешивания монет». The American Mathematical Monthly . 102 (2): 164–167. doi :10.1080/00029890.1995.11990553.
4. Гроссман, Говард (1945). Scripta Mathematica XI .
5. "Math Forum - Ask Dr. Math". mathforum.org . Архивировано из оригинала 2002-06-12.
6. Хованова, Таня (2013). «Решение задачи о фальшивой монете и ее обобщение». arXiv : 1310.7268 [math.HO].
7. Чуднов, Александр М. (2015). «Весовые алгоритмы классификации и идентификации ситуаций». Дискретная математика и приложения . 25 (2): 69–81. doi :10.1515/dma-2015-0007. S2CID  124796871.

Внешние ссылки

• Игровой пример второй головоломки
• Двухчашечные весы и обобщенная проблема фальшивой монеты