Фильтр с распределенными элементами

Тип схемы электронного фильтра

Фильтр с распределенными элементами — это электронный фильтр , в котором емкость , индуктивность и сопротивление ( элементы схемы) не локализованы в дискретных конденсаторах , индукторах и резисторах , как в обычных фильтрах. Его цель — пропускать диапазон частот сигнала , но блокировать другие. Обычные фильтры состоят из индукторов и конденсаторов, а схемы, построенные таким образом, описываются моделью сосредоточенных элементов , которая рассматривает каждый элемент как «собранный вместе» в одном месте. Эта модель концептуально проста, но становится все более ненадежной по мере увеличения частоты сигнала или, что эквивалентно, по мере уменьшения длины волны . Модель распределенных элементов применяется на всех частотах и ​​используется в теории линий передачи ; многие компоненты распределенных элементов состоят из коротких отрезков линии передачи. В распределенном представлении схем элементы распределены по длине проводников и неразрывно перемешаны друг с другом. Конструкция фильтра обычно касается только индуктивности и емкости, но из-за этого смешивания элементов их нельзя рассматривать как отдельные "сосредоточенные" конденсаторы и индукторы. Не существует точной частоты, выше которой должны использоваться фильтры с распределенными элементами, но они особенно связаны с микроволновым диапазоном (длина волны менее одного метра).

Фильтры с распределенными элементами используются во многих из тех же приложений, что и фильтры с сосредоточенными элементами, таких как селективность радиоканала, ограничение полосы шума и мультиплексирование многих сигналов в один канал. Фильтры с распределенными элементами могут быть сконструированы так, чтобы иметь любую из возможных форм полосы с сосредоточенными элементами ( фильтр нижних частот , полосовой фильтр и т. д.), за исключением фильтра верхних частот , который обычно только аппроксимируется. Все классы фильтров, используемые в конструкциях с сосредоточенными элементами ( Баттерворта , Чебышева и т. д.), могут быть реализованы с использованием подхода с распределенными элементами.

Существует много форм компонентов, используемых для построения фильтров с распределенными элементами, но все они имеют общее свойство вызывать разрыв на линии передачи. Эти разрывы представляют реактивное сопротивление волновому фронту, движущемуся по линии, и эти реактивные сопротивления могут быть выбраны по конструкции, чтобы служить приближениями для сосредоточенных индуктивностей , конденсаторов или резонаторов , как того требует фильтр. ^[4]

Разработка фильтров с распределенными элементами была вызвана военной потребностью в радарах и мерах электронного противодействия во время Второй мировой войны. Аналоговые фильтры с сосредоточенными элементами были разработаны задолго до этого, но эти новые военные системы работали на микроволновых частотах, и требовались новые конструкции фильтров. Когда война закончилась, технология нашла применение в микроволновых линиях связи , используемых телефонными компаниями и другими организациями с крупными фиксированными сетями связи, такими как телевизионные вещатели. В настоящее время эту технологию можно найти в нескольких потребительских товарах массового производства, таких как преобразователи (на рисунке 1 показан пример), используемые со спутниковыми телевизионными антеннами .

Общие комментарии

Рисунок 2. Фильтр с параллельными линиями в микрополосковой конструкции

Символ λ используется для обозначения длины волны сигнала, передаваемого по линии или участку линии данной электрической длины .

Фильтры с распределенными элементами в основном используются на частотах выше диапазона VHF (Very High Frequency) (от 30 до 300 МГц ). На этих частотах физическая длина пассивных компонентов составляет значительную часть длины волны рабочей частоты, и становится трудно использовать обычную модель сосредоточенных элементов . Точная точка, в которой становится необходимым моделирование с распределенными элементами, зависит от конкретной рассматриваемой конструкции. Общее правило заключается в применении моделирования с распределенными элементами, когда размеры компонентов больше 0,1λ. Растущая миниатюризация электроники привела к тому, что конструкции схем становятся все меньше по сравнению с λ. Частоты, за пределами которых подход с распределенными элементами для проектирования фильтров становится необходимым, становятся все выше в результате этих достижений. С другой стороны, размеры структуры антенны обычно сопоставимы с λ во всех частотных диапазонах и требуют модели с распределенными элементами. ^[5]

Наиболее заметное различие в поведении между фильтром с распределенными элементами и его приближением с сосредоточенными элементами заключается в том, что первый будет иметь несколько копий полосы пропускания прототипа с сосредоточенными элементами , поскольку характеристики передачи линии передачи повторяются с гармоническими интервалами. Эти паразитные полосы пропускания нежелательны в большинстве случаев. ^[6]

Для ясности представления диаграммы в этой статье нарисованы с компонентами, реализованными в формате полосковой линии . Это не подразумевает отраслевого предпочтения, хотя форматы планарных линий передачи (то есть форматы, в которых проводники состоят из плоских полосок) популярны, поскольку они могут быть реализованы с использованием устоявшихся технологий изготовления печатных плат . Показанные структуры также могут быть реализованы с использованием микрополосковых или скрытых полосковых технологий (с соответствующими корректировками размеров) и могут быть адаптированы к коаксиальным кабелям , двойным выводам и волноводам , хотя некоторые структуры больше подходят для некоторых реализаций, чем другие. Реализации открытого провода, например, ряда структур показаны во втором столбце рисунка 3, а эквиваленты открытого провода можно найти для большинства других структур полосковых линий. Планарные линии передачи также используются в конструкциях интегральных схем . ^[7]

История

Разработка фильтров с распределенными элементами началась за несколько лет до Второй мировой войны. Уоррен П. Мейсон основал область схем с распределенными элементами . ^[8] Основная статья по этой теме была опубликована Мейсоном и Сайксом в 1937 году. ^[9] Мейсон подал патент ^[10] гораздо раньше, в 1927 году, и этот патент может содержать первую опубликованную электрическую конструкцию, которая отходит от анализа сосредоточенных элементов. ^[11] Работа Мейсона и Сайкса была сосредоточена на форматах коаксиального кабеля и сбалансированных пар проводов — планарные технологии еще не использовались. Большая часть разработок была выполнена в военные годы, обусловленных потребностями фильтрации радаров и электронных контрмер . Значительная часть этого была в Радиационной лаборатории Массачусетского технологического института , ^[12] но другие лаборатории в США и Великобритании также были вовлечены. ^{[13] [14]}

Требовались некоторые важные достижения в теории сетей, прежде чем фильтры могли быть развиты за пределами военных конструкций. Одной из них была теория соразмерных линий Пола Ричардса . ^[15] Соразмерные линии — это сети, в которых все элементы имеют одинаковую длину (или в некоторых случаях кратную единичной длине), хотя они могут отличаться в других измерениях, давая различные характеристические импедансы. Преобразование Ричардса позволяет взять сосредоточенную конструкцию элемента «как есть» и преобразовать ее непосредственно в конструкцию с распределенными элементами, используя очень простое уравнение преобразования. ^[16]

Трудность преобразования Ричардса с точки зрения построения практических фильтров заключалась в том, что полученная конструкция с распределенными элементами неизменно включала последовательно соединенные элементы. Это было невозможно реализовать в планарных технологиях и часто было неудобно в других технологиях. Эта проблема была решена К. Куродой, который использовал трансформаторы импеданса для устранения последовательных элементов. Он опубликовал набор преобразований, известных как тождества Куроды, в 1955 году, но его работа была написана на японском языке, и прошло несколько лет, прежде чем его идеи были включены в англоязычную литературу. ^[17]

После войны одним из важных направлений исследований была попытка увеличить проектную полосу пропускания широкополосных фильтров. Подход, который использовался в то время (и используется до сих пор), заключался в том, чтобы начать с прототипа фильтра с сосредоточенными элементами и с помощью различных преобразований прийти к желаемому фильтру в форме распределенных элементов. Этот подход, по-видимому, застрял на минимальном значении Q, равном пяти (см. Полосовые фильтры ниже для объяснения Q ). В 1957 году Лео Янг ​​из Стэнфордского исследовательского института опубликовал метод проектирования фильтров, который начинался с прототипа с распределенными элементами. ^[18] Этот прототип был основан на четвертьволновых трансформаторах импеданса и мог производить конструкции с полосой пропускания до октавы , что соответствовало Q около 1,3. Некоторые из процедур Янга в этой статье были эмпирическими, но позже ^[19] были опубликованы точные решения. Статья Янга конкретно посвящена непосредственно связанным объемным резонаторам, но эта процедура может быть в равной степени применена к другим типам непосредственно связанных резонаторов, например, тем, которые встречаются в современных планарных технологиях и проиллюстрированы в этой статье. Фильтр с емкостным зазором (рисунок 8) и фильтр с параллельно связанными линиями (рисунок 9) являются примерами непосредственно связанных резонаторов. ^[16]

Рисунок 3. В первом столбце показаны некоторые простые планарные структуры фильтров. Во втором столбце показана эквивалентная схема с разомкнутым проводом для этих структур. Третий столбец представляет собой приближение полусосредоточенных элементов, где элементы, обозначенные K или J, являются трансформаторами импеданса или проводимости соответственно. Четвертый столбец показывает приближение сосредоточенных элементов, делая дальнейшее предположение, что трансформаторы импеданса являются трансформаторами λ/4.

1. Короткозамкнутый шлейф, параллельный основной линии.
2. Разомкнутый шлейф, параллельный основной линии.
3. Короткозамкнутая линия, соединенная с основной линией.
4. Связанные короткозамкнутые линии.
5. Связанные разомкнутые линии.

представляет собой полосу, проходящую через плату и соединяющуюся с заземляющей плоскостью под ней.

Внедрение печатных планарных технологий значительно упростило производство многих микроволновых компонентов, включая фильтры, и микроволновые интегральные схемы затем стали возможными. Неизвестно, когда появились планарные линии передачи, но эксперименты с их использованием были зарегистрированы еще в 1936 году. ^[20] Однако изобретатель печатной полосковой линии известен; это был Роберт М. Барретт, который опубликовал идею в 1951 году. ^{[21] Это быстро завоевало популярность, и} полосковая линия Барретта вскоре столкнулась с жесткой коммерческой конкуренцией со стороны конкурирующих планарных форматов, особенно трехслойных и микрополосковых . Общий термин полосковая линия в современном использовании обычно относится к форме, тогда известной как трехслойная . ^[22]

Ранние полосковые фильтры с прямым резонатором были соединены на конце, но длина была уменьшена, а компактность последовательно увеличилась с введением параллельно-связанных линейных фильтров, ^[23] встречно-штыревых фильтров, ^[24] и гребенчатых фильтров. ^[25] Большая часть этой работы была опубликована группой в Стэнфорде под руководством Джорджа Маттеи, а также включая Лео Янга, упомянутого выше, в знаковой книге, которая до сих пор служит справочником для разработчиков схем. ^{[26] [27]} Шпильковый фильтр был впервые описан в 1972 году . ^{[28] [29]} К 1970-м годам было описано большинство топологий фильтров, которые сегодня широко используются. ^[30] Более поздние исследования были сосредоточены на новых или различных математических классах фильтров, таких как псевдоэллиптические , при этом все еще использовались те же основные топологии или с альтернативными технологиями реализации, такими как подвешенные полосковые и плавниковые . ^[31]

Первоначальное невоенное применение фильтров с распределенными элементами было в микроволновых линиях связи , используемых телекоммуникационными компаниями для обеспечения опоры своих сетей. Эти линии связи также использовались другими отраслями с большими фиксированными сетями, в частности, телевизионными вещателями. ^[32] Такие приложения были частью крупных программ капиталовложений. Однако массовое производство сделало технологию достаточно дешевой для внедрения в отечественные системы спутникового телевидения . ^[33] Новое применение — сверхпроводящие фильтры для использования в базовых станциях сотовой связи, эксплуатируемых компаниями мобильной связи. ^[34]

Основные компоненты

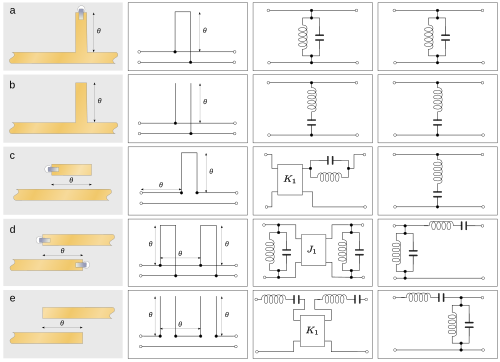
Простейшая структура, которую можно реализовать, — это ступенька в характеристическом сопротивлении линии, которая вносит разрыв в характеристики передачи. В планарных технологиях это делается путем изменения ширины линии передачи. На рисунке 4(a) показана ступенька вверх по импедансу (более узкие линии имеют более высокое сопротивление). Ступенька вниз по импедансу будет зеркальным отражением рисунка 4(a). Разрыв можно приблизительно представить как последовательный индуктор или, точнее, как низкочастотную Т-образную схему, как показано на рисунке 4(a). ^[35] Множественные разрывы часто соединяются вместе с трансформаторами импеданса для создания фильтра более высокого порядка . Эти трансформаторы импеданса могут быть всего лишь короткой (часто λ/4) длиной линии передачи. Эти составные структуры могут реализовать любое из семейств фильтров ( Баттерворта , Чебышева и т. д.) путем аппроксимации рациональной передаточной функции соответствующего фильтра с сосредоточенными элементами. Это соответствие не является точным, поскольку схемы с распределенными элементами не могут быть рациональными и являются основной причиной расхождения поведения сосредоточенных и распределенных элементов. Трансформаторы импеданса также используются в гибридных смесях фильтров с сосредоточенными и распределенными элементами (так называемые полусосредоточенные структуры). ^[36]

Рисунок 4. Еще больше полосковых элементов и их аналогов с сосредоточенными параметрами.

1. Резкий ступенчатый импеданс. ^[35]
2. Линия резко обрывается. ^[35]
3. Отверстие или щель в линии. ^[37]
4. Поперечный полуразрез поперек линии. ^[38]
5. Разрыв в линии. ^[38]

Другим очень распространенным компонентом фильтров с распределенными элементами является шлейф . В узком диапазоне частот шлейф может использоваться как конденсатор или индуктор (его импеданс определяется его длиной), но в широком диапазоне он ведет себя как резонатор. Короткозамкнутые, номинально четвертьволновые шлейфы (рисунок 3(a)) ведут себя как шунтирующие LC- антирезонаторы , а разомкнутый номинально четвертьволновый шлейф (рисунок 3(b)) ведет себя как последовательный LC- резонатор . Шлейфы также могут использоваться в сочетании с трансформаторами импеданса для построения более сложных фильтров и, как и следовало ожидать из их резонансной природы, наиболее полезны в полосовых приложениях. ^[39] Хотя шлейфы с разомкнутой цепью проще изготавливать в планарных технологиях, у них есть тот недостаток, что окончание значительно отклоняется от идеальной разомкнутой цепи (см. рисунок 4(b)), что часто приводит к предпочтению шлейфов с коротким замыканием (один всегда можно использовать вместо другого, добавляя или вычитая λ/4 к длине или из нее). ^[35]

Спиральный резонатор похож на заглушку, поскольку для его представления требуется модель с распределенными элементами, но на самом деле он построен с использованием сосредоточенных элементов. Они построены в непланарном формате и состоят из катушки провода на каркасе и сердечнике и соединены только с одного конца. Устройство обычно находится в экранированной банке с отверстием в верхней части для регулировки сердечника. Он часто будет выглядеть физически очень похожим на сосредоточенные LC-резонаторы, используемые для аналогичной цели. Они наиболее полезны в верхних диапазонах VHF и нижних диапазонах UHF, тогда как заглушки чаще применяются в верхних диапазонах UHF и SHF . ^[40]

Связанные линии (рисунки 3(ce)) также могут использоваться в качестве фильтрующих элементов; подобно шлейфам, они могут действовать как резонаторы и также быть завершены коротким замыканием или разомкнутой цепью. Связанные линии, как правило, предпочтительны в планарных технологиях, где их легко реализовать, тогда как шлейфы, как правило, предпочтительны в других местах. Реализация настоящей разомкнутой цепи в планарной технологии невозможна из-за диэлектрического эффекта подложки, который всегда будет гарантировать, что эквивалентная цепь содержит шунтирующую емкость. Несмотря на это, разомкнутые цепи часто используются в планарных форматах вместо коротких замыканий, потому что их проще реализовать. Многочисленные типы элементов можно классифицировать как связанные линии, и выбор наиболее распространенных из них показан на рисунках. ^[41]

Некоторые общие структуры показаны на рисунках 3 и 4 вместе с их аналогами с сосредоточенными элементами. Эти приближения с сосредоточенными элементами не следует воспринимать как эквивалентные схемы, а скорее как руководство по поведению распределенных элементов в определенном диапазоне частот. На рисунках 3(a) и 3(b) показаны шлейф с коротким замыканием и разомкнутой цепью соответственно. Когда длина шлейфа равна λ/4, они ведут себя соответственно как антирезонаторы и резонаторы и поэтому полезны соответственно как элементы в полосовых и режекторных фильтрах . На рисунке 3(c) показана короткозамкнутая линия, соединенная с основной линией. Она также ведет себя как резонатор, но обычно используется в приложениях с фильтрами нижних частот с резонансной частотой, находящейся далеко за пределами интересующей полосы. На рисунках 3(d) и 3(e) показаны связанные линейные структуры, которые обе полезны в полосовых фильтрах. Структуры рисунков 3(c) и 3(e) имеют эквивалентные схемы, включающие шлейфы, размещенные последовательно с линией. Такая топология проста в реализации в схемах с открытым проводом, но не с планарной технологией. Поэтому эти две структуры полезны для реализации эквивалентного последовательного элемента. ^[42]

Фильтры нижних частот

Микрополосковый фильтр нижних частот, реализованный с использованием шлейфов типа «бабочка» внутри анализатора спектра Agilent N9344C с частотой 20 ГГц

Рисунок 5. Фильтр нижних частот со ступенчатым импедансом, образованный чередующимися высоко- и низкоомными участками линии.

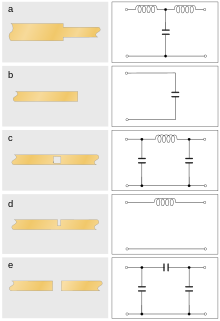
Фильтр нижних частот может быть реализован довольно непосредственно из прототипа сосредоточенных элементов лестничной топологии с фильтром ступенчатого импеданса, показанным на рисунке 5. Это также называется конструкцией каскадных линий . Фильтр состоит из чередующихся секций линий с высоким и низким импедансом, которые соответствуют последовательным индукторам и шунтирующим конденсаторам в реализации сосредоточенных элементов. Фильтры нижних частот обычно используются для подачи смещения постоянного тока (DC) на активные компоненты. Фильтры, предназначенные для этого применения, иногда называют дросселями . В таких случаях каждый элемент фильтра имеет длину λ/4 (где λ — длина волны сигнала основной линии, которая должна быть заблокирована от передачи в источник постоянного тока), а секции линии с высоким импедансом делаются настолько узкими, насколько позволяет технология производства, чтобы максимизировать индуктивность. ^[43] Дополнительные секции могут быть добавлены по мере необходимости для производительности фильтра, как и для аналога сосредоточенных элементов. Помимо показанной плоской формы, эта структура особенно хорошо подходит для коаксиальных реализаций с чередующимися дисками из металла и изолятора, нанизанными на центральный проводник. ^{[44] [45] [46]}

Рисунок 6. Другая форма фильтра нижних частот со ступенчатым импедансом, включающая шунтирующие резонаторы.

Более сложный пример конструкции ступенчатого импеданса представлен на рисунке 6. Опять же, узкие линии используются для реализации индукторов, а широкие линии соответствуют конденсаторам, но в этом случае аналог с сосредоточенными элементами имеет резонаторы, подключенные шунтированно через основную линию. Эта топология может использоваться для проектирования эллиптических фильтров или фильтров Чебышева с полюсами затухания в полосе задерживания . Однако расчет значений компонентов для этих структур является сложным процессом и привел к тому, что проектировщики часто выбирают вместо этого реализацию их как m-производных фильтров , которые хорошо работают и намного проще в расчетах. Целью включения резонаторов является улучшение подавления полосы задерживания . Однако за пределами резонансной частоты резонатора с самой высокой частотой подавление полосы задерживания начинает ухудшаться по мере того, как резонаторы движутся к разомкнутой цепи. По этой причине фильтры, построенные по этой конструкции, часто имеют дополнительный одиночный конденсатор со ступенчатым импедансом в качестве конечного элемента фильтра. ^[47] Это также обеспечивает хорошее подавление на высокой частоте. ^{[48] ​​[49] [50]}

Рисунок 7. Фильтры нижних частот, построенные из шлейфов.

1. Стандартные заглушки по разные стороны от основной линии на расстоянии λ/4 друг от друга.
2. Похожая конструкция с использованием заглушек-бабочек.
3. Различные формы пеньков, соответственно, двойные параллельные пеньки, радиальный пенек, пенек в виде бабочки (параллельные радиальные пеньки), пенек в виде листа клевера (тройные параллельные радиальные пеньки).

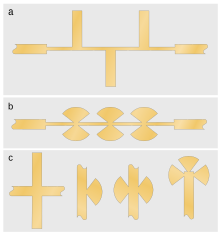
Другой распространенный метод проектирования нижних частот заключается в реализации шунтирующих конденсаторов в качестве шлейфов с резонансной частотой, установленной выше рабочей частоты, так что импеданс шлейфа является емкостным в полосе пропускания. Эта реализация имеет сосредоточенный элементный аналог общей формы, аналогичной фильтру на рисунке 6. Там, где позволяет пространство, шлейфы могут быть установлены по разные стороны от основной линии, как показано на рисунке 7(a). Цель этого состоит в том, чтобы предотвратить связь между соседними шлейфами, которая ухудшает работу фильтра за счет изменения частотной характеристики. Однако структура со всеми шлейфами на одной стороне все еще является допустимой конструкцией. Если шлейф должен быть линией с очень низким импедансом, шлейф может быть неудобно широким. В этих случаях возможным решением является параллельное соединение двух более узких шлейфов. То есть, каждое положение шлейфа имеет шлейф с обеих сторон линии. Недостатком этой топологии является то, что возможны дополнительные поперечные резонансные моды вдоль длины линии λ/2, образованной двумя шлейфами вместе. Для конструкции дросселя требуется просто сделать емкость как можно больше, для чего максимальная ширина шлейфа λ/4 может использоваться с шлейфами, параллельными по обе стороны от основной линии. Полученный фильтр выглядит довольно похожим на фильтр со ступенчатым импедансом на рисунке 5, но был разработан на совершенно других принципах. ^[43] Трудность с использованием шлейфов такой ширины заключается в том, что точка, в которой они подключаются к основной линии, плохо определена. Шлейф, который узкий по сравнению с λ, можно считать подключенным по его центральной линии, и расчеты, основанные на этом предположении, точно предскажут реакцию фильтра. Однако для широкого шлейфа расчеты, которые предполагают, что боковая ветвь подключена в определенной точке на основной линии, приводят к неточностям, поскольку это больше не является хорошей моделью схемы передачи. Одним из решений этой трудности является использование радиальных шлейфов вместо линейных шлейфов. Пара радиальных заглушек, расположенных параллельно (по одной с каждой стороны от основной линии), называется заглушкой-бабочкой (см. рисунок 7(b)). Группа из трех радиальных заглушек, расположенных параллельно, которая может быть получена в конце линии, называется заглушкой-клеверным листом. ^{[51] [52]}

Полосовые фильтры

Полосовой фильтр может быть построен с использованием любых элементов, которые могут резонировать. Фильтры, использующие шлейфы, могут быть, очевидно, сделаны полосовыми; возможны многочисленные другие структуры, и некоторые из них представлены ниже.

Важным параметром при обсуждении полосовых фильтров является дробная полоса пропускания. Она определяется как отношение полосы пропускания к геометрической центральной частоте. Обратное этой величине называется добротностью , Q. Если ω ₁ и ω ₂ являются частотами краев полосы пропускания, то: ^[53]

пропускная способность , ${\displaystyle \Delta \omega =\omega _{2}-\omega _{1}\,}$

геометрическая центральная частота и ${\displaystyle \omega _{0}={\sqrt {\omega _{1}\omega _{2}}}}$

${\displaystyle Q={\frac {\omega _{0}}{\Delta \omega }}}$

Фильтр емкостного зазора

Рисунок 8. Емкостный полосковый фильтр

Структура емкостного зазора состоит из секций линии длиной около λ/2, которые действуют как резонаторы и соединены «торец-на-торец» зазорами в линии передачи. Она особенно подходит для планарных форматов, легко реализуется с помощью технологии печатных схем и имеет то преимущество, что занимает не больше места, чем простая линия передачи. Ограничением этой топологии является то, что производительность (особенно вносимые потери ) ухудшается с увеличением дробной полосы пропускания, и приемлемые результаты не достигаются при Q менее примерно 5. Еще одна трудность с созданием конструкций с низкой добротностью заключается в том, что ширина зазора должна быть меньше для более широких дробных полос пропускания. Минимальная ширина зазоров, как и минимальная ширина дорожек , ограничена разрешением технологии печати. ^{​​[46] [54]}

Фильтр с параллельными линиями

Рисунок 9. Фильтр с параллельными полосковыми линиями. Этот фильтр обычно печатается под углом, как показано, чтобы минимизировать занимаемое пространство на плате, хотя это не является существенной особенностью конструкции. Также обычно конечный элемент или перекрывающиеся половины двух конечных элементов имеют меньшую ширину для целей согласования (не показано на этой схеме, см. Рисунок 1).

Параллельно-связанные линии — еще одна популярная топология для печатных плат, для которой линии с разомкнутой цепью являются наиболее простыми для реализации, поскольку производство состоит не более чем из печатной дорожки. Конструкция состоит из ряда параллельных резонаторов λ/2, но связывающих только λ/4 с каждым из соседних резонаторов, таким образом образуя ступенчатую линию, как показано на рисунке 9. С этим фильтром возможны более широкие дробные полосы пропускания, чем с фильтром с емкостным зазором, но аналогичная проблема возникает на печатных платах, поскольку диэлектрические потери уменьшают Q. Линии с более низкой Q требуют более плотной связи и меньших зазоров между ними, что ограничено точностью процесса печати. ​​Одним из решений этой проблемы является печать дорожки на нескольких слоях с перекрытием соседних линий, но не в контакте, поскольку они находятся на разных слоях. Таким образом, линии могут быть связаны по всей их ширине, что приводит к гораздо более сильной связи, чем когда они находятся от края к краю, и становится возможным больший зазор для той же производительности. ^[55]

Микрополосковый шпилечный фильтр, за которым следует низкочастотный шлейфовый фильтр на печатной плате в 20-гигагерцовом спектроанализаторе Agilent N9344C

Для других (непечатных) технологий линии короткого замыкания могут быть предпочтительными, поскольку короткое замыкание обеспечивает механическую точку крепления для линии, а диэлектрические изоляторы, снижающие добротность , не требуются для механической поддержки. За исключением механических и сборочных причин, существует небольшое предпочтение для линий с разомкнутой цепью по сравнению с линиями с коротким замыканием. Обе структуры могут реализовать тот же диапазон реализаций фильтров с теми же электрическими характеристиками. Оба типа параллельно связанных фильтров, в теории, не имеют паразитных полос пропускания на удвоенной центральной частоте, как это наблюдается во многих других топологиях фильтров (например, шлейфы). Однако подавление этой паразитной полосы пропускания требует идеальной настройки связанных линий, что не реализуется на практике, поэтому неизбежно существует некоторая остаточная паразитная полоса пропускания на этой частоте. ^{[46] [56] [57]}

Микрополосковый штифтовой фильтр на печатной плате, реализованный в спектроанализаторе Agilent N9344C

Фильтр-шпилька — это еще одна структура, которая использует параллельно связанные линии. В этом случае каждая пара параллельно связанных линий соединена со следующей парой короткой связью. Образованные таким образом U-образные формы дают начало названию фильтр- шпилька . В некоторых конструкциях связь может быть длиннее, что дает широкую шпильку с действием трансформатора импеданса λ/4 между секциями. ^{[58] [59]}

Рисунок 10. Полосковый шпилечный фильтр

Угловые изгибы, показанные на рисунке 10, обычны для полосковых конструкций и представляют собой компромисс между острым прямым углом, который создает большой разрыв, и плавным изгибом, который занимает большую площадь платы, которая может быть сильно ограничена в некоторых продуктах. Такие изгибы часто встречаются в длинных шлейфах, где они не могли бы быть вставлены в имеющееся пространство. Эквивалентная схема с сосредоточенными элементами такого рода разрыва похожа на разрыв ступенчатого импеданса. ^[38] Примеры таких шлейфов можно увидеть на входах смещения нескольких компонентов на фотографии в верхней части статьи. ^{[46] [60]}

Фильтр встречно-штыревой

Рисунок 11. Полосковый встречно-штыревой фильтр

Три фильтра со встречно-штыревыми связями на печатной плате анализатора спектра

Встречно-штыревые фильтры являются еще одной формой фильтра связанных линий. Каждая секция линии имеет длину около λ/4 и заканчивается коротким замыканием только на одном конце, другой конец остается разомкнутым. Короткозамкнутый конец чередуется на каждой секции линии. Эта топология проста в реализации в планарных технологиях, но также особенно подходит для механической сборки линий, закрепленных внутри металлического корпуса. Линии могут быть как круглыми стержнями, так и прямоугольными брусками, а сопряжение с линией коаксиального формата является простым. Как и в случае с фильтром параллельных линий, преимущество механической компоновки, которая не требует изоляторов для поддержки, заключается в том, что диэлектрические потери устраняются. Требование к расстоянию между линиями не такое строгое, как в структуре параллельных линий; таким образом, можно достичь более высокой дробной полосы пропускания, и возможны значения Q вплоть до 1,4. ^{[61] [62]}

Фильтр гребенчатой ​​линии похож на встречно-штыревой фильтр в том, что он поддается механической сборке в металлическом корпусе без диэлектрической поддержки. В случае гребенчатой ​​линии все линии закорочены на одном конце, а не на альтернативных. Другие концы заканчиваются конденсаторами на землю, и конструкция, следовательно, классифицируется как полусосредоточенная. Главное преимущество этой конструкции заключается в том, что верхняя полоса задерживания может быть сделана очень широкой, то есть свободной от паразитных полос пропускания на всех частотах, представляющих интерес. ^[63]

Фильтры полосовые заглушки

Рисунок 12. Полосковый шлейфовый фильтр, состоящий из короткозамкнутых шлейфов λ/4

Как упоминалось выше, шлейфы подходят для полосовых конструкций. Общие формы их похожи на шлейфовые фильтры нижних частот, за исключением того, что основная линия больше не является узкой линией с высоким импедансом. Разработчики имеют на выбор множество различных топологий шлейфовых фильтров, некоторые из которых дают идентичные отклики. Пример шлейфового фильтра показан на рисунке 12; он состоит из ряда шлейфов короткого замыкания λ/4, соединенных вместе трансформаторами импеданса λ/4.

Шлейфы в корпусе фильтра представляют собой двойные параллельные шлейфы, в то время как шлейфы на концевых секциях являются только одинарными, что имеет преимущества согласования импеданса. Трансформаторы импеданса имеют эффект преобразования ряда шунтирующих антирезонаторов в лестницу последовательных резонаторов и шунтирующих антирезонаторов. Фильтр с аналогичными свойствами может быть построен с λ/4 разомкнутыми шлейфами, размещенными последовательно с линией и соединенными вместе с λ/4 трансформаторами импеданса, хотя эта структура невозможна в планарных технологиях. ^[64]

Еще одна доступная структура — это шлейфы с разомкнутой цепью λ/2 по всей линии, соединенные с трансформаторами импеданса λ/4. Эта топология имеет как низкочастотные, так и полосовые характеристики. Поскольку она пропускает постоянный ток, можно передавать смещающие напряжения на активные компоненты без необходимости в блокировочных конденсаторах. Кроме того, поскольку не требуются короткозамкнутые связи, не требуются никакие операции по сборке, кроме печати платы, при реализации в виде полосковой линии. Недостатки:

(i) фильтр займет больше места на плате, чем соответствующий фильтр-заглушка λ/4, поскольку все заглушки в два раза длиннее;

(ii) первая паразитная полоса пропускания находится на уровне 2ω ₀ , в отличие от 3ω ₀ для λ/4-заглушенного фильтра. ^[65]

Рисунок 13. 60°-образный обрубок бабочки Кониси

Кониши описывает широкополосный полосовой фильтр 12 ГГц, который использует 60° бабочкообразные шлейфы и также имеет низкочастотный отклик (короткозамкнутые шлейфы требуются для предотвращения такого отклика). Как это часто бывает с фильтрами с распределенными элементами, полоса, в которую классифицируется фильтр, во многом зависит от того, какие полосы желательны, а какие считаются побочными. ^[66]

Фильтры верхних частот

Настоящие фильтры верхних частот трудно, если не невозможно, реализовать с распределенными элементами. Обычный подход к проектированию заключается в том, чтобы начать с полосового дизайна, но сделать верхнюю полосу задерживания на частоте, которая настолько высока, что не представляет интереса. Такие фильтры описываются как псевдо-фильтры верхних частот, а верхняя полоса задерживания описывается как остаточная полоса задерживания. Даже структуры, которые, как кажется, имеют «очевидную» топологию верхних частот, такие как фильтр с емкостным зазором на рисунке 8, оказываются полосовыми, если рассмотреть их поведение для очень коротких длин волн. ^[67]

Смотрите также

• Портал электроники

• Фильтр ВЧ и СВЧ
• Волноводный фильтр
• Шпора
• Делители мощности и направленные ответвители

Ссылки

1. Бахл, стр. 290–293.
2. Бенуа, стр. 44–51.
3. Лундстрём, стр.80–82
4. Коннор, стр. 13–14.
5. Голио, стр. 1.2–1.3, 4.4–4.5.
6. Маттеи и др. , стр. 17–18.
7. Роджерс и др. , стр. 129.
8. Терстон, стр. 570
9. Мейсон и Сайкс, 1937.
10. Мейсон, Уоррен П., «Волновой фильтр», патент США 1,781,469 , подан: 25 июня 1927 г., выдан: 11 ноября 1930 г.
11. Фейген и Миллман, стр. 108.
12. Раган, 1965.
13. Макимото и Ямасита, стр.2.
14. Леви и Кон, стр.1055.
15. Ричардс, 1948.
16. Леви и Кон, стр. 1056.
17. Леви и Кон, стр.1057.
18. Янг, 1963.
19. Леви, 1967.
20. Аксун, стр.142.
21. Барретт и Барнс, 1951,
    Барретт, 1952,
    Нихенке и др. , стр. 846.
22. Саркар, стр. 556–559.
23. Кон, 1958.
24. Маттеи, 1962.
25. Маттеи, 1963.
26. Маттеи и др. , 1964.
27. Леви и Кон, стр. 1057–1059.
28. Кристал и Франкель, 1972.
29. Леви и Кон, стр.1063.
30. Нихенке и др. , стр. 847.
31. Леви и Кон, стр.1065.
32. Хюрдеман, стр. 369–371.
33. Бенуа, стр.34.
34. Форд и Сондерс, стр. 157–159.
35. Бхат и Коул, стр.498.
36. Маттеи и др. , стр. 144–149, 203–207.
37. Бхат и Коул, стр. 539.
38. Бхат и Коул, стр.499.
39. Маттеи и др. , стр. 203–207.
40. Карр, стр. 63–64.
41. Маттеи и др. , стр. 217–218.
42. Маттеи и др. , стр. 217–229.
43. Kneppo, стр. 213–214.
44. Маттеи и др. , стр. 373–374.
45. Ли, стр. 789–790.
46. Севги, стр.252.
47. Хонг и Ланкастер, стр.117.
48. Маттеи и др. , стр. 373–380.
49. Ли, стр. 792–794.
50. Кнеппо, стр.212.
51. Ли, стр. 790–792.
52. Кнеппо, стр. 212–213.
53. Фараго, стр.69.
54. Маттеи и др. , стр. 422, 440–450.
55. Маттеи и др. , стр. 585–595.
56. Маттеи и др. , стр. 422, 472–477.
57. Кнеппо, стр. 216–221.
58. Хонг и Ланкастер, стр. 130–132.
59. Джарри и Бенеат, стр. 15.
60. Паоло, стр. 113–116.
61. Маттеи и др. , стр. 424, 614–632.
62. Хонг и Ланкастер, стр. 140.
63. Маттеи и др. , стр. 424, 497–518.
64. Маттеи и др. , стр. 595–605.
65. Маттеи и др. , стр. 605–614.
66. Кониси, стр. 80–82.
67. Маттеи и др. , стр. 541.

Библиография

• Бахл, И. Дж. Сосредоточенные элементы для ВЧ и СВЧ цепей, Artech House, 2003 ISBN  1-58053-309-4 .
• Барретт, Р.М. и Барнс, М.Х. «Микроволновые печатные схемы», Radio Telev. , т.46 , стр. 16, сентябрь 1951 г.
• Барретт, Р.М. «Протравленные листы служат микроволновыми компонентами», Электроника , т.25 , стр. 114–118, июнь 1952 г.
• Бенуа, Эрве Спутниковое телевидение: методы аналогового и цифрового телевидения , Butterworth-Heinemann, 1999 ISBN 0-340-74108-2 . 
• Бхат, Бхарати и Коул, Шибан К. Полосковые линии передачи для СВЧ-интегральных схем, New Age International, 1989 ISBN 81-224-0052-3 . 
• Карр, Джозеф Дж. Справочник по радиоприемникам для технических специалистов, Newnes, 2001 ISBN 0-7506-7319-2 
• Кон, С.Б. «Параллельно-связанные резонаторные фильтры линий передачи», Труды IRE: Теория и техника СВЧ , т. MTT-6 , стр. 223–231, апрель 1958 г.
• Коннор, FR Передача волн , Edward Arnold Ltd., 1972 ISBN 0-7131-3278-7 . 
• Кристал, Э.Г. и Франкель, С. «Фильтры со шпильковой линией/полуволновыми параллельными связанными линиями», Труды IEEE: Теория и методы СВЧ , т. MTT-20 , стр. 719–728, ноябрь 1972 г.
• Фейген, М.Д. и Миллман, С. История инженерии и науки в системе Белла: Том 5: Науки о связи (1925–1980) , AT&T Bell Laboratories, 1984.
• Фараго, П.С. Введение в линейный сетевой анализ , English Universities Press, 1961.
• Форд, Питер Джон и Сондерс, Дж. А. Возникновение сверхпроводников , CRC Press, 2005 ISBN 0-7484-0772-3 . 
• Голио, Джон Майкл. Справочник по радиочастотам и микроволнам , CRC Press, 2001 ISBN 0-8493-8592-X . 
• Хонг, Цзя-Шенг и Ланкастер, М.Дж. Микрополосковые фильтры для ВЧ/СВЧ-применений, John Wiley and Sons, 2001 ISBN 0-471-38877-7 . 
• Хюрдеман, Антон А. Всемирная история телекоммуникаций , Wiley-IEEE, 2003 ISBN 0-471-20505-2 . 
• Жарри, Пьер и Бенеат, Жак. Проектирование и реализация миниатюрных фрактальных СВЧ- и ВЧ-фильтров , John Wiley and Sons, 2009 ISBN 0-470-48781-X . 
• Кнеппо, Иван Микроволновые интегральные схемы, Springer, 1994 ISBN 0-412-54700-7 . 
• Кониси, Ёсихиро Микроволновые интегральные схемы, CRC Press, 1991 ISBN 0-8247-8199-6 . 
• Ли, Томас Х. Планарная микроволновая техника: практическое руководство по теории, измерениям и схемам, Cambridge University Press, 2004 ISBN 0-521-83526-7 . 
• Леви, Р. «Теория фильтров с прямыми связанными резонаторами», Труды IEEE: Теория и методы СВЧ , т. MTT-15 , стр. 340–348, июнь 1967 г.
• Леви, Р. Кон, С.Б., «История исследований, проектирования и разработки микроволновых фильтров», Труды IEEE: Теория и методы микроволнового излучения , стр. 1055–1067, т. 32 , выпуск 9, 1984.
• Лундстрем, Ларс-Ингемар Понимание цифрового телевидения , Elsevier, 2006 ISBN 0-240-80906-8 . 
• Макимото, Мицуо и Ямашита, Садахико «Микроволновые резонаторы и фильтры для беспроводной связи: теория, конструкция и применение», Springer, 2001 ISBN 3-540-67535-3 . 
• Мейсон, У. П. и Сайкс, Р. А. «Использование коаксиальных и сбалансированных линий передачи в фильтрах и широкополосных трансформаторах для высоких радиочастот», Bell Syst. Tech. J. , т. 16 , стр. 275–302, 1937.
• Маттеи, Г.Л. «Встречно-штыревые полосовые фильтры», Труды IRE: Теория и техника СВЧ , т. MTT-10 , стр. 479–491, ноябрь 1962 г.
• Маттеи, Г.Л. «Полосовые фильтры гребенчатого типа с узкой или умеренной полосой пропускания», Microwave Journal , т. 6 , стр. 82–91, август 1963 г.
• Маттеи, Джордж Л.; Янг, Лео и Джонс, EMT Микроволновые фильтры, сети согласования импеданса и структуры связи. McGraw-Hill, 1964 (издание 1980 года — ISBN 0-89006-099-1 ). 
• Нихенке, EC; Пусель, RA и Бал, IJ «Интегральные схемы СВЧ и миллиметрового диапазона», IEEE Transactions: Microwave Theory and Techniques , ' т.50 , выпуск 3 марта 2002 г., стр.846–857.
• Ди Паоло, Франко Сети и устройства, использующие планарные линии передачи, CRC Press, 2000 ISBN 0-8493-1835-1 . 
• Раган, Г.Л. (ред.) Схемы передачи микроволнового излучения , Лаборатория радиации Массачусетского технологического института, Dover Publications, 1965.
• Ричардс, П.И. «Цепи резистивной линии передачи», Труды IRE , т. 36 , стр. 217–220, февраль 1948 г.
• Роджерс, Джон В. М. и Плетт, Кэлвин. Проектирование интегральных радиочастотных схем, Artech House, 2003 ISBN 1-58053-502-X . 
• Саркар, Тапан К. История беспроводной связи , John Wiley and Sons, 2006 ISBN 0-471-71814-9 . 
• Севги, Левент. Сложные электромагнитные проблемы и методы численного моделирования, Wiley-IEEE, 2003 ISBN 0-471-43062-5 . 
• Терстон, Роберт Н., «Уоррен П. Мейсон: 1900-1986», Журнал Акустического общества Америки , т. 81, вып. 2, стр. 570-571, февраль 1987 г.
• Янг, Л. «Фильтры с прямой связью резонаторов для широких и узких полос пропускания» Труды IEEE: Теория и методы СВЧ , т. MTT-11 , стр. 162–178, май 1963 г.