Греки (финансы)

В математических финансах греки — это величины (известные в исчислении как частные производные ; первого порядка или выше), представляющие чувствительность цены производного инструмента, такого как опцион, к изменениям одного или нескольких базовых параметров , от которых зависит стоимость инструмента или портфеля финансовых инструментов . Название используется потому, что наиболее распространенные из этих чувствительности обозначаются греческими буквами (как и некоторые другие финансовые меры). В совокупности они также называются чувствительностью к риску , ^[1] мерами риска ^[2]^{: 742} или параметрами хеджирования . ^[3]

Использование греков

Греки являются важными инструментами в управлении рисками . Каждый грек измеряет чувствительность стоимости портфеля к небольшому изменению заданного базового параметра, так что риски компонентов могут рассматриваться изолированно, а портфель соответствующим образом перебалансируется для достижения желаемого уровня воздействия; см., например, дельта-хеджирование .

Греки в модели Блэка-Шоулза (относительно простая идеализированная модель некоторых финансовых рынков) относительно легко вычисляются — желательное свойство финансовых моделей — и очень полезны для трейдеров деривативов, особенно тех, кто стремится хеджировать свои портфели от неблагоприятных изменений рыночных условий. По этой причине те греки, которые особенно полезны для хеджирования — такие как дельта, тета и вега — хорошо определены для измерения изменений параметров спотовой цены, времени и волатильности. Хотя ро (частная производная по безрисковой процентной ставке ) является основным входом в модель Блэка-Шоулза, общее влияние на стоимость краткосрочного опциона, соответствующее изменениям безрисковой процентной ставки, как правило, незначительно, и поэтому производные инструменты более высокого порядка, включающие безрисковую процентную ставку, не распространены.

Наиболее распространенными из греков являются производные первого порядка: дельта, вега, тета и ро; а также гамма, производная второго порядка функции стоимости. Оставшиеся чувствительности в этом списке достаточно распространены, чтобы иметь общие названия, но этот список ни в коем случае не является исчерпывающим.

Игроки на рынке совершают конкурентные сделки, включающие многие миллиарды ($, £ или €) базовых активов каждый день, поэтому важно правильно рассчитать суммы. На практике они будут использовать более сложные модели, которые выходят за рамки упрощающих предположений, используемых в модели Блэка-Шоулза и, следовательно, в Греках.

Имена

Использование названий греческих букв, предположительно, является расширением общих финансовых терминов альфа и бета , а также использования сигмы (стандартное отклонение логарифмической доходности) и тау (время до истечения срока) в модели ценообразования опционов Блэка-Шоулза . Несколько названий, таких как «вега» (символ которого похож на строчную греческую букву ню ; использование этого названия могло бы привести к путанице) и «зомма», придуманы, но звучат похоже на греческие буквы. Названия «цвет» и «очарование» предположительно происходят от использования этих терминов для экзотических свойств кварков в физике элементарных частиц .

Греки первого порядка

Дельта

Дельта ,^[4] , измеряет скорость изменения теоретической стоимости опциона по отношению к изменениям в цене базового актива. Дельта — это первая производная стоимостиопциона по отношению к цене базового инструмента. $\Дельта$ $V$ $S$

\Delta ={\frac {\partial V}{\partial S}}

Практическое использование

Для ванильного опциона дельта будет числом от 0,0 до 1,0 для длинного колла (или короткого пута) и от 0,0 до −1,0 для длинного пута (или короткого колла); в зависимости от цены, опцион колл ведет себя так, как будто вы владеете 1 акцией базового актива (если глубоко в деньгах), или не владеете ничем (если далеко не в деньгах), или чем-то средним, и наоборот для опциона пут. Разница между дельтой колла и дельтой пут с тем же страйком равна единице. По паритету пут-колл длинный колл и короткий пут эквивалентны форварду F , который линеен в споте S с единичным множителем, поэтому производная dF/dS равна 1. См. формулы ниже.

Эти числа обычно представляются в процентах от общего количества акций, представленных опционным контрактом(ами). Это удобно, поскольку опцион будет (мгновенно) вести себя как количество акций, указанное дельтой. Например, если портфель из 100 американских опционов колл на XYZ каждый имеет дельту 0,25 (= 25%), он будет расти или падать в цене так же, как 2500 акций XYZ, поскольку цена меняется при небольших колебаниях цены (100 опционных контрактов покрывают 10 000 акций). Знак и процент часто опускаются — знак подразумевается в типе опциона (отрицательный для пут, положительный для колл), а процент понятен. Чаще всего котируются 25 дельта пут, 50 дельта пут/50 дельта колл и 25 дельта колл. 50 дельта пут и 50 дельта колл не совсем идентичны из-за разницы в споте и форварде на коэффициент дисконтирования, но их часто объединяют.

Дельта всегда положительна для длинных коллов и отрицательна для длинных путов (если они не равны нулю). Общая дельта сложного портфеля позиций по одному и тому же базовому активу может быть рассчитана путем простого подсчета суммы дельт для каждой отдельной позиции — дельта портфеля линейна по составляющим. Поскольку дельта базового актива всегда равна 1,0, трейдер может дельта-хеджировать всю свою позицию по базовому активу, покупая или продавая в шорт количество акций, указанное общей дельтой. Например, если дельта портфеля опционов на XYZ (выраженная в акциях базового актива) составляет +2,75, трейдер сможет дельта-хеджировать портфель, продав в шорт 2,75 акций базового актива. Этот портфель затем сохранит свою общую стоимость независимо от того, в каком направлении будет двигаться цена XYZ. (Хотя только для небольших движений базового актива, короткого периода времени и несмотря на изменения других рыночных условий, таких как волатильность и норма прибыли для безрисковых инвестиций).

Как показатель вероятности

(Абсолютное значение) Дельты близко, но не идентично процентной денежности опциона, т. е. подразумеваемой вероятности того, что опцион истечет в деньгах (если рынок движется в соответствии с броуновским движением в нейтральной к риску мере ). ^[5] По этой причине некоторые трейдеры опционов используют абсолютное значение дельты в качестве приближения для процентной денежности. Например, если опцион колл вне денег имеет дельту 0,15, трейдер может оценить, что у опциона есть приблизительно 15% шанс истечь в деньгах. Аналогично, если контракт пут имеет дельту −0,25, трейдер может ожидать, что у опциона будет 25% вероятность истечения в деньгах. Коллы и путы в деньгах имеют дельту приблизительно 0,5 и −0,5 соответственно с небольшим смещением в сторону более высоких дельт для коллов в деньгах, поскольку безрисковая ставка вносит некоторое смещение в дельту. Отрицательная дисконтированная вероятность того, что опцион окажется в деньгах по истечении срока, называется двойной дельтой, которая является первой производной цены опциона по отношению к страйку. ^[6]

Соотношение между колл и пут дельта

При наличии европейского опциона колл и пут на один и тот же базовый актив, цену исполнения и время до погашения, а также при отсутствии дивидендной доходности сумма абсолютных значений дельты каждого опциона будет равна 1 — точнее, дельта колла (положительная) минус дельта пут (отрицательная) равна 1. Это происходит из-за паритета пут-колл : длинный колл плюс короткий пут (колл минус пут) воспроизводят форвард, дельта которого равна 1.

Если значение дельты для опциона известно, можно рассчитать значение дельты опциона с той же ценой исполнения, базовым активом и датой погашения, но с противоположными значениями, вычитая 1 из известной дельты колл или прибавляя 1 к известной дельте пут.

\Delta ({\text{call}})-\Delta ({\text{put}})=1,{\text{ therefore: }}\Delta ({\text{call}})=\Delta ({\text{put}})+1{\text{ and }}\Delta ({\text{put}})=\Delta ({\text{call}})-1.

Например, если дельта колла составляет 0,42, то можно вычислить дельту соответствующего пута при той же цене исполнения по формуле 0,42 − 1 = −0,58. Чтобы вывести дельту колла из пута, можно аналогичным образом взять −0,58 и добавить 1, чтобы получить 0,42.

Вега

Вега ^[4] измеряет чувствительность к волатильности . Вега — это производная стоимости опциона по волатильности базового актива.

{\mathcal {V}}={\frac {\partial V}{\partial \sigma }}

Vega не является названием какой-либо греческой буквы. Используемый глиф представляет собой нестандартную маюскульную версию греческой буквы nu ( ), написанную как . Предположительно, название vega было принято потому, что греческая буква nu выглядела как латинская vee , а vega произошло от vee по аналогии с тем, как beta , eta , и theta произносятся в американском английском. ${\textstyle \nu }$ ${\mathcal {V}}$

Символ каппа , , иногда используется (учеными) вместо веги (как и тау ( ) или заглавная лямбда ( ), ^[7]^{: 315,} хотя они встречаются редко). $\kappa$ $\tau$ $\Lambda$

Вега обычно выражается как сумма денег на базовую акцию, на которую стоимость опциона увеличится или уменьшится при росте или падении волатильности на 1 процентный пункт . Все опционы (как колл, так и пут) будут увеличивать стоимость при росте волатильности.

Vega может быть важным греческим индикатором для отслеживания опционным трейдером, особенно на волатильных рынках, поскольку стоимость некоторых опционных стратегий может быть особенно чувствительна к изменениям волатильности. Стоимость опциона «при деньгах» (at-the-money) straddle , например, чрезвычайно зависит от изменений волатильности. См. Риск волатильности .

Тета

Тета ,^[4] , измеряет чувствительность значения производной к течению времени (см. Опция временного значения ): «временной спад». $\Theta$

\Theta =-{\frac {\partial V}{\partial \tau }}

С течением времени, с уменьшением времени до истечения срока и при прочих равных условиях внешняя стоимость опциона уменьшается. Обычно (но см. ниже) это означает, что опцион теряет стоимость со временем, что традиционно называется длинными опционами, как правило, имеющими короткую (отрицательную) тету. Фактически, обычно буквальная первая производная по времени стоимости опциона является положительным числом. Изменение стоимости опциона обычно отрицательно, потому что течение времени является отрицательным числом ( уменьшение до , времени до истечения срока). Однако по соглашению практики обычно предпочитают называть воздействие теты («спад») длинного опциона отрицательным (вместо течения времени отрицательным), и поэтому тета обычно сообщается как -1, умноженное на первую производную, как указано выше. $\tau \,$

В то время как внешняя стоимость уменьшается с течением времени, иногда уравновешивающим фактором является дисконтирование. Для опционов deep-in-the-money некоторых типов (для путов в Black-Scholes, путов и коллов в Black's), поскольку факторы дисконтирования увеличиваются до 1 с течением времени, это является элементом увеличения стоимости в длинном опционе. Иногда опционы deep-in-the-money больше выигрывают от увеличения факторов дисконтирования, чем теряют от уменьшения внешней стоимости, и сообщаемая тета будет положительным значением для длинного опциона вместо более типичного отрицательного значения (и опцион будет кандидатом на раннее исполнение, если он может быть исполнен, и европейский опцион может стать менее паритетным).

По соглашению в формулах оценки опционов, время до истечения срока определяется в годах. Практикующие специалисты обычно предпочитают рассматривать тету с точки зрения изменения количества дней до истечения срока, а не количества лет до истечения срока. Поэтому сообщаемая тета обычно делится на количество дней в году. (Считать ли календарные дни или рабочие дни, зависит от личного выбора, и есть аргументы в пользу обоих вариантов.) $\tau \,$

Ро

Rho ,^[4] , измеряет чувствительность к процентной ставке: это производная стоимости опциона по отношению к безрисковой процентной ставке (для соответствующего срока погашения). $\rho$

\rho ={\frac {\partial V}{\partial r}}

За исключением экстремальных обстоятельств, стоимость опциона менее чувствительна к изменениям безрисковой процентной ставки, чем к изменениям других параметров. По этой причине rho является наименее используемым из греков первого порядка.

Rho обычно выражается как сумма денег в расчете на акцию базового актива, на которую увеличится или уменьшится стоимость опциона при повышении или понижении безрисковой процентной ставки на 1,0% годовых (100 базисных пунктов).

Лямбда

Лямбда^[4] , омега [^8] или эластичность [^4] — это процентное изменение стоимости опциона на процентное изменение базовой цены, мера кредитного плеча , иногда называемая заемным капиталом. $\lambda$ $\Omega$

\lambda =\Omega ={\frac {\partial V}{\partial S}}\times {\frac {S}{V}}

Он утверждает, что . $\lambda =\Omega =\Delta \times {\frac {S}{V}}$

Это похоже на концепцию дельты, но выражается в процентах, а не в абсолютных величинах.

Эпсилон

Эпсилон [^9] (также известный как psi,) — это процентное изменение стоимости опциона на процентное изменение базовой дивидендной доходности, мера дивидендного риска. Влияние дивидендной доходности на практике определяется с использованием 10%-ного увеличения этих доходностей. Очевидно, что эта чувствительность может применяться только к производным инструментам акционерных продуктов. $\varepsilon$ $\psi$

\varepsilon =\psi ={\frac {\partial V}{\partial q}}

В числовом выражении все чувствительности первого порядка можно интерпретировать как спреды ожидаемых доходов. ^[10] Информационная геометрия предлагает другую (тригонометрическую) интерпретацию. ^[10]

Греки второго порядка

Гамма

Гамма ,^[4] , измеряет скорость изменения дельты относительно изменений базовой цены. Гамма является второй производной функции стоимости относительно базовой цены. $\Gamma$

\Gamma ={\frac {\partial \Delta }{\partial S}}={\frac {\partial ^{2}V}{\partial S^{2}}}

Большинство длинных опционов имеют положительную гамму, а большинство коротких опционов — отрицательную гамму. Длинные опционы имеют положительную связь с гаммой, поскольку по мере роста цены гамма также увеличивается, заставляя Дельту приближаться к 1 от 0 (длинный опцион колл) и к 0 от −1 (длинный опцион пут). Обратное верно для коротких опционов. ^[11]

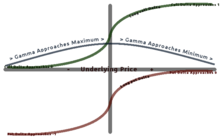
Гамма имеет наибольшее значение около «при деньгах» (ATM) и уменьшается по мере того, как вы выходите из игры, либо «в деньгах» (ITM), либо «вне денег» (OTM). Гамма важна, поскольку она корректирует выпуклость стоимости .

Когда трейдер стремится создать эффективный дельта-хедж для портфеля, он также может попытаться нейтрализовать гамму портфеля, поскольку это гарантирует, что хедж будет эффективным в более широком диапазоне базовых ценовых движений.

Ванна

Vanna , ^[4] также называемая DvegaDspot ^[13] и DdeltaDvol , ^[13] является производной второго порядка от стоимости опциона, один раз по базовой спотовой цене и один раз по волатильности. Она математически эквивалентна DdeltaDvol , чувствительности дельты опциона по отношению к изменению волатильности; или, альтернативно, парциальной веге по отношению к цене базового инструмента. Vanna может быть полезной чувствительностью для мониторинга при поддержании дельта- или вега-хеджированного портфеля, поскольку vanna поможет трейдеру предвидеть изменения эффективности дельта-хеджа по мере изменения волатильности или эффективности вега-хеджа по отношению к изменению базовой спотовой цены.

Если базовая стоимость имеет непрерывные вторые частные производные, то ${\text{Vanna}}={\frac {\partial \Delta }{\partial \sigma }}={\frac {\partial {\mathcal {V}}}{\partial S}}={\frac {\partial ^{2}V}{\partial S\,\partial \sigma }}.$

Очарование

Очарование ^[4] или дельта-распад ^[14] измеряют мгновенную скорость изменения дельты с течением времени.

{\text{Charm}}=-{\frac {\partial \Delta }{\partial \tau }}={\frac {\partial \Theta }{\partial S}}=-{\frac {\partial ^{2}V}{\partial \tau \,\partial S}}

Charm также называется DdeltaDtime . ^[13] Charm может быть важным греческим для измерения/контроля при дельта-хеджировании позиции в течение выходных. Charm является производной второго порядка от стоимости опциона, один раз по цене и один раз по течению времени. Это также производная тета по отношению к цене базового актива.

Математический результат формулы для очарования (см. ниже) выражается в дельта/год. Часто бывает полезно разделить это на количество дней в году, чтобы получить дельта-распад за день. Такое использование довольно точно, когда количество дней, оставшихся до истечения срока опциона, велико. Когда опцион приближается к истечению, само очарование может быстро измениться, делая полные дневные оценки дельта-распада неточными.

Вомма

Vomma , ^[4] volga , ^[15] vega convexity , ^[15] или DvegaDvol ^[15] измеряет чувствительность второго порядка к волатильности . Vomma — это вторая производная стоимости опциона по волатильности, или, другими словами, vomma измеряет скорость изменения веги при изменении волатильности.

{\text{Vomma}}={\frac {\partial {\mathcal {V}}}{\partial \sigma }}={\frac {\partial ^{2}V}{\partial \sigma ^{2}}}

При положительной vomma позиция станет длинной вега, когда подразумеваемая волатильность увеличится, и короткой вега, когда она уменьшится, что может быть скальпировано аналогично длинной гамме. И изначально вега-нейтральная, длинная вомма позиция может быть построена из соотношений опционов с разными страйками. Vomma положительна для длинных опционов вдали от денег и изначально увеличивается с расстоянием от денег (но падает, когда падает вега). (В частности, vomma положительна, когда обычные термины d ₁ и d ₂ имеют одинаковый знак, что верно, когда d ₁ < 0 или d ₂ > 0.)

Вета

Вета , ^[16] распад веги или DvegaDtime ^[15] измеряет скорость изменения веги по отношению к течению времени. Вета — вторая производная функции стоимости; один раз по волатильности и один раз по времени.

{\text{Veta}}={\frac {\partial {\mathcal {V}}}{\partial \tau }}={\frac {\partial ^{2}V}{\partial \sigma \,\partial \tau }}

Обычно математический результат веты делят на 100, умноженное на количество дней в году, чтобы свести значение к процентному изменению веги за один день.

Вера

Vera ^[17] (иногда rhova ) ^[17] измеряет скорость изменения rho относительно волатильности. Vera — вторая производная функции стоимости; один раз по волатильности и один раз по процентной ставке.

{\text{Vera}}={\frac {\partial \rho }{\partial \sigma }}={\frac {\partial ^{2}V}{\partial \sigma \,\partial r}}

Слово «Vera» было придумано Р. Нарышкиным в начале 2012 года, когда эту чувствительность нужно было использовать на практике для оценки влияния изменений волатильности на ро-хеджирование, но в доступной литературе еще не было названия. «Vera» было выбрано, чтобы оно звучало похоже на комбинацию Вега и Ро, соответствующих греков первого порядка. Это название теперь используется более широко, включая, например, программное обеспечение компьютерной алгебры Maple (в пакете Finance которого есть функция «BlackScholesVera»).

Частная производная второго порядка по ударуК

Эта частная производная играет фундаментальную роль в формуле Бридена–Литценбергера ^[18] , которая использует котируемые цены опционов колл для оценки нейтральных по отношению к риску вероятностей, подразумеваемых такими ценами.

\varpi ={\frac {\partial ^{2}V}{\partial K^{2}}}

Для опционов колл его можно аппроксимировать с помощью бесконечно малых портфелей стратегий «бабочки» .

Греки третьего порядка

Скорость

Скорость ^[4] измеряет скорость изменения Гаммы по отношению к изменениям базовой цены.

{\text{Speed}}={\frac {\partial \Gamma }{\partial S}}={\frac {\partial ^{3}V}{\partial S^{3}}}

Это также иногда называют гаммой гаммы ^[2]^{: 799} или DgammaDspot . ^[13] Скорость является третьей производной функции стоимости относительно базовой спотовой цены. Скорость может быть важна для мониторинга при дельта-хеджировании или гамма-хеджировании портфеля.

Зомма

Зомма ^[4] измеряет скорость изменения гаммы по отношению к изменениям волатильности.

{\text{Zomma}}={\frac {\partial \Gamma }{\partial \sigma }}={\frac {\partial {\text{vanna}}}{\partial S}}={\frac {\partial ^{3}V}{\partial S^{2}\,\partial \sigma }}

Zomma также упоминается как DgammaDvol . ^[13] Zomma — это третья производная от стоимости опциона, дважды по цене базового актива и один раз по волатильности. Zomma может быть полезной чувствительностью для мониторинга при поддержании гамма-хеджированного портфеля, поскольку zomma поможет трейдеру предвидеть изменения эффективности хеджа по мере изменения волатильности.

Цвет

Цвет ^[13] , гамма-распад ^[19] или DgammaDtime ^[13] измеряет скорость изменения гамма-излучения с течением времени.

{\text{Color}}={\frac {\partial \Gamma }{\partial \tau }}={\frac {\partial ^{3}V}{\partial S^{2}\,\partial \tau }}

Цвет — производная третьего порядка от стоимости опциона, дважды по цене базового актива и один раз по времени. Цвет может быть важным показателем чувствительности, который нужно контролировать при поддержании гамма-хеджированного портфеля, поскольку он может помочь трейдеру предвидеть эффективность хеджа с течением времени.

Математический результат формулы для цвета (см. ниже) выражается в гамме в год. Часто бывает полезно разделить это на количество дней в году, чтобы получить изменение гаммы в день. Такое использование довольно точно, когда количество дней, оставшихся до истечения срока опциона, велико. Когда опцион приближается к истечению, сам цвет может быстро измениться, делая полные дневные оценки изменения гаммы неточными.

Ультима

Ultima ^[4] измеряет чувствительность опциона vomma по отношению к изменению волатильности.

{\text{Ultima}}={\frac {\partial {\text{vomma}}}{\partial \sigma }}={\frac {\partial ^{3}V}{\partial \sigma ^{3}}}

Ultima также упоминается как DvommaDvol . ^[4] Ultima — это производная третьего порядка от стоимости опциона по волатильности.

Пармичарма

Пармичарма ^[4] измеряет скорость изменения очарования с течением времени.

{\text{Parmicharma}}=-{\frac {\partial {\text{charm}}}{\partial \tau }}={\frac {\partial ^{3}V}{\partial \tau ^{2}\partial S}}

Parmicharma также упоминается как DcharmDtime . ^[20] Parmicharma — это производная третьего порядка от стоимости опциона, дважды по времени и один раз по цене базового актива. Чтобы лучше поддерживать портфель с дельта-хеджем с течением времени, трейдер может хеджировать charm в дополнение к своей текущей позиции delta. ^[20] Parmicharma может быть полезной чувствительностью для мониторинга при поддержании такого портфеля с чарм-хеджем, поскольку parmicharma поможет трейдеру предвидеть изменения эффективности хеджа с течением времени.

Греки за опционы на несколько активов

Если стоимость производного инструмента зависит от двух или более базовых активов , его греки расширяются, чтобы включить перекрестные эффекты между базовыми активами.

Дельта корреляции измеряет чувствительность значения производной от изменения корреляции между базовыми активами. ^[21] Также широко известна как cega . ^[22]^[23]

Кросс-гамма измеряет скорость изменения дельты одного базового актива по отношению к изменению уровня другого базового актива. ^[24]

Cross vanna измеряет скорость изменения веги в одном базовом активе из-за изменения уровня другого базового актива. Эквивалентно, он измеряет скорость изменения дельты во втором базовом активе из-за изменения волатильности первого базового актива. ^[21]

Кросс-волга измеряет скорость изменения веги одного базового актива по отношению к изменению волатильности другого базового актива. ^[24]

Формулы для европейских опционов Греки

Греки европейских опционов ( коллы и путы ) по модели Блэка-Шоулза рассчитываются следующим образом, где (phi) — стандартная нормальная функция плотности вероятности , а — стандартная нормальная кумулятивная функция распределения . Обратите внимание, что формулы гаммы и веги одинаковы для коллов и путов. $\varphi$ $\Phi$

Для данного:

Цена акций , $S\,$
Цена исполнения , $K\,$
Безрисковая ставка , $r\,$
Годовая дивидендная доходность , $q\,$
Время до погашения (представлено как безразмерная часть одного года) и $\tau =T-t\,$
Волатильность . $\sigma \,$

где

{\begin{aligned}d_{1}&={\frac {\ln(S/K)+\left(r-q+{\frac {1}{2}}\sigma ^{2}\right)\tau }{\sigma {\sqrt {\tau }}}}\\d_{2}&={\frac {\ln(S/K)+\left(r-q-{\frac {1}{2}}\sigma ^{2}\right)\tau }{\sigma {\sqrt {\tau }}}}=d_{1}-\sigma {\sqrt {\tau }}\\\varphi (x)&={\frac {1}{\sqrt {2\pi }}}e^{-{\frac {1}{2}}x^{2}}\\\Phi (x)&={\frac {1}{\sqrt {2\pi }}}\int _{-\infty }^{x}e^{-{\frac {1}{2}}y^{2}}\,dy=1-{\frac {1}{\sqrt {2\pi }}}\int _{x}^{\infty }e^{-{\frac {1}{2}}y^{2}}\,dy\end{aligned}}

Согласно модели Блэка (обычно используемой для товаров и опционов на фьючерсы), греки можно рассчитать следующим образом:

где

{\begin{aligned}d_{1}&={\frac {\ln(F/K)+{\frac {1}{2}}\sigma ^{2}\tau }{\sigma {\sqrt {\tau }}}}\\d_{2}&={\frac {\ln(F/K)-{\frac {1}{2}}\sigma ^{2}\tau }{\sigma {\sqrt {\tau }}}}=d_{1}-\sigma {\sqrt {\tau }}\end{aligned}}

(*) Можно показать, что $F\varphi (d_{1})=K\varphi (d_{2})$

Микродоказательство:

позволять $x=\sigma {\sqrt {\tau }}$
$d_{1}={\frac {\ln {\frac {F}{K}}+{\frac {1}{2}}x^{2}}{x}}$
$d_{1}\cdot x=\ln {\frac {F}{K}}+{\frac {1}{2}}x^{2}$
$\ln(F/K)=d_{1}\cdot x-{\frac {1}{2}}x^{2}$
${\frac {F}{K}}=e^{d_{1}\cdot x-{\frac {1}{2}}x^{2}}$
Тогда имеем: ${\frac {F}{K}}\cdot {\frac {\varphi (d_{1})}{\varphi (d_{2})}}={\frac {F}{K}}\cdot e^{{\frac {1}{2}}\cdot {d_{2}}^{2}-{\frac {1}{2}}\cdot {d_{1}}^{2}}$
$=e^{d_{1}x-{\frac {1}{2}}x^{2}}\cdot e^{{\frac {1}{2}}\cdot {(d_{1}-x)}^{2}-{\frac {1}{2}}\cdot {d_{1}}^{2}}=e^{d_{1}x-{\frac {1}{2}}x^{2}+{\frac {1}{2}}\cdot (2d_{1}-x)(-x)}=e^{0}=1.$
Так $F\varphi (d_{1})=K\varphi (d_{2})$

Сопутствующие меры

Ниже перечислены некоторые сопутствующие меры риска финансовых инструментов .

Длительность и выпуклость связи

В торговле облигациями и другими ценными бумагами с фиксированным доходом различные меры длительности облигаций используются аналогично дельте опциона. Ближайшим аналогом дельты является DV01 , который представляет собой снижение цены (в денежных единицах) при увеличении доходности на один базисный пункт (т. е. 0,01% годовых) , где доходность является базовой переменной; см. Длительность облигаций § Риск – длительность как чувствительность к процентной ставке . (Связано с CS01 , измеряющим чувствительность к кредитному спреду .)

Аналогом лямбды является модифицированная дюрация , которая представляет собой процентное изменение рыночной цены облигации(ий) для единичного изменения доходности (т. е. она эквивалентна DV01, деленной на рыночную цену). В отличие от лямбды, которая представляет собой эластичность ( процентное изменение выпуска для процентного изменения ввода), модифицированная дюрация представляет собой полуэластичность — процентное изменение выпуска для единичного изменения ввода. См. также Дюрация ключевой ставки .

Выпуклость облигаций — это мера чувствительности дюрации к изменениям процентных ставок , вторая производная цены облигации по отношению к процентным ставкам (дюрация — первая производная); тогда она аналогична гамме. В общем, чем выше выпуклость, тем более чувствительна цена облигации к изменению процентных ставок. Выпуклость облигаций — одна из самых основных и широко используемых форм выпуклости в финансах .

Для облигации со встроенным опционом стандартные расчеты доходности к погашению здесь не учитывают, как изменения процентных ставок изменят денежные потоки из-за исполнения опциона. Чтобы решить эту проблему, вводятся эффективная дюрация и эффективная выпуклость . Эти значения обычно рассчитываются с использованием древовидной модели, построенной для всей кривой доходности (в отличие от одной доходности к погашению), и, следовательно, фиксирующей поведение исполнения в каждой точке срока действия опциона как функцию как времени, так и процентных ставок; см. Модель решетки (финансы) § Производные процентных ставок .

Бета

Бета (β) акций или портфеля — это число, описывающее волатильность актива по отношению к волатильности эталона, с которым сравнивается данный актив. Этот эталон обычно представляет собой весь финансовый рынок и часто оценивается с помощью репрезентативных индексов , таких как S&P 500 .

Актив имеет бету, равную нулю, если его доходность изменяется независимо от изменений доходности рынка. Положительная бета означает, что доходность актива в целом следует за доходностью рынка, в том смысле, что они оба имеют тенденцию быть выше своих средних значений вместе или оба имеют тенденцию быть ниже своих средних значений вместе. Отрицательная бета означает, что доходность актива в целом движется в направлении, противоположном доходности рынка: одна будет иметь тенденцию быть выше своего среднего значения, когда другая будет ниже своего среднего значения.

Фугит

Fugit — это ожидаемое время исполнения американского или бермудского опциона. Fugit полезно вычислять для целей хеджирования — например, можно представить потоки американского свопциона как потоки свопа, начинающиеся с fugit, умноженные на дельту, а затем использовать их для вычисления других чувствительности.

Смотрите также

Ссылки

^ Бэнкс, Эрик; Сигел, Пол (2006). Справочник по опционам: методы хеджирования и спекуляции для профессиональных инвесторов . McGraw-Hill Professional . стр. 263. ISBN 9780071453158.
^ ab Macmillan, Lawrence G. (1993). Опционы как стратегические инвестиции (3-е изд.). Нью-Йоркский институт финансов . ISBN 978-0-13-636002-5.
^ Крисс, Нил (1996). Блэк–Шоулз и далее: модели ценообразования опционов. McGraw-Hill Professional . стр. 308. ISBN 9780786310258.
^ abcdefghijklmno Хауг, Эспен Гарднер (2007). Полное руководство по формулам ценообразования опционов . McGraw-Hill Professional . ISBN 9780071389976.
^ Сума, Джон. "Опционы Греки: Дельта Риск и Вознаграждение" . Получено 7 января 2010 г.
^ Штайнер, Боб (2013). Освоение финансовых расчетов (3-е изд.). Pearson UK. ISBN 9780273750604.
^ Халл, Джон К. (1993). Опционы, фьючерсы и другие производные ценные бумаги (2-е изд.). Prentice-Hall . ISBN 9780136390145.
^ Омега – Инвестопедия
^ De Spiegeleer, Jan; Schoutens, Wim, ред. (2012). «Измерение риска». Справочник по конвертируемым облигациям . стр. 227–294. doi :10.1002/9781118374696.ch9. ISBN 978-0-470-68968-4.
^ ab Соклаков, AN (2023). «Информационная геометрия рисков и доходностей». Риск . Июнь . arXiv : 2206.08753 . SSRN 4134885.
^ Уиллетт, Джефф (28.05.2014). «Понимание того, как гамма влияет на дельту». www.traderbrains.com . Получено 07.03.2014 .
^ Уиллетт, Джефф (28.05.2014). «Почему гамма длинных опционов положительна». www.traderbrains.com . Получено 07.03.2014 .
^ abcdefg Хауг, Эспен Гаардер (2003), «Знай свое оружие, часть 1» (PDF) , Wilmott Magazine (май 2003 г.): 49–57, doi :10.1002/wilm.42820030313 (неактивен 2024-03-19){{citation}}: CS1 maint: DOI inactive as of March 2024 (link)
^ Деривативы – Дельта-распад – Финансовая энциклопедия
^ abcd Haug, Эспен Гордер (2003), «Знай свое оружие, часть 2», журнал Wilmott Magazine (июль 2003 г.): 43–57
^ Урсоне, Пьерино (2015). «Вега». Как рассчитать цены опционов и их греки . стр. 93–110. doi :10.1002/9781119011651.ch9. ISBN 978-1-119-01162-0.
^ ab Производные – Греки второго порядка – Финансовая энциклопедия
^ Бриден, Дуглас Т.; Литценбергер, Роберт Х. (1978). «Цены зависящих от состояния требований, подразумеваемые в ценах опционов». The Journal of Business . 51 (4): 621–651. doi :10.1086/296025. JSTOR 2352653. SSRN 2642349.
^ "Деривативы – Греки". Инвестиции и финансы . Получено 21.12.2020 .
^ ab Mastinsek, Miklavz (весна 2012 г.). «Charm-Adjusted Delta and Delta Gamma Hedging». Журнал Derivatives . 19 (3): 69–76. doi :10.3905/jod.2012.19.3.069. ProQuest 963355778.
^ ab "Греки за опционы на несколько активов" . Получено 24 января 2017 г.
^ Риск корреляции . Получено 22 марта 2018 г.
^ "Варианты вращающегося горного хребта, оценка и риски / Анализ эффективности" . Получено 22 марта 2018 г. .
^ ab Fengler, Matthias R.; Schwendner, Peter (13 февраля 2003 г.). Премии за риск корреляции для опционов на акции с несколькими активами (отчет). doi : 10.18452/3572 .

Внешние ссылки

Теория

Дельта, Гамма, ГаммаП, Гамма-симметрия, Ванна, Скорость, Очарование, Седло Гамма: Ванильные варианты — Эспен Хауг,
Волга, Ванна, Скорость, Очарование, Цвет: Ванильные опции - Уве Выступ Архивировано 28.09.2007 в Wayback Machine , Ванильные опции - Уве Выступ

Онлайн-инструменты

Греки: Чувствительность цен финансовых опционов, пакет R для вычисления греков для европейских, американских и азиатских опционов