Большой отрыв ближайшего соседа

Статистический алгоритм машинного обучения для метрического обучения

Классификация с большим запасом ближайшего соседа ( LMNN ) ^[1] — это статистический алгоритм машинного обучения для метрического обучения . Он изучает псевдометрику, разработанную для классификации k-ближайших соседей . Алгоритм основан на полуопределенном программировании , подклассе выпуклой оптимизации .

Целью контролируемого обучения (точнее классификации) является изучение правила принятия решения, которое может классифицировать экземпляры данных по предопределенным классам. Правило k-ближайших соседей предполагает наличие обучающего набора данных из помеченных экземпляров (т. е. классы известны). Оно классифицирует новый экземпляр данных с классом, полученным из большинства голосов k ближайших (помеченных) обучающих экземпляров. Близость измеряется с помощью предопределенной метрики . Алгоритм Large margin neighbors изучает эту глобальную (псевдо-)метрику контролируемым образом для повышения точности классификации правила k-ближайших соседей.

Настраивать

Основная идея LMNN — изучить псевдометрику, при которой все экземпляры данных в обучающем наборе окружены по крайней мере k экземплярами, имеющими ту же метку класса. Если это достигнуто, ошибка исключения одного элемента (особый случай перекрестной проверки ) сводится к минимуму. Пусть обучающие данные состоят из набора данных , где набор возможных категорий классов равен . ${\displaystyle D=\{({\vec {x}}_{1},y_{1}),\dots ,({\vec {x}}_{n},y_{n})\}\subset R^{d}\times C}$ ${\displaystyle C=\{1,\dots ,c\}}$

Алгоритм изучает псевдометрику типа

${\displaystyle d({\vec {x}}_{i},{\vec {x}}_{j})=({\vec {x}}_{i}-{\vec {x}}_{j})^{\top }\mathbf {M} ({\vec {x}}_{i}-{\vec {x}}_{j})}$.

Для того, чтобы быть хорошо определенной, матрица должна быть положительно полуопределенной . Евклидова метрика является частным случаем, где — единичная матрица. Это обобщение часто (ошибочно ^{[ требуется цитата ]} ) называют метрикой Махаланобиса . ${\displaystyle d(\cdot ,\cdot )}$ ${\displaystyle \mathbf {M} }$ ${\displaystyle \mathbf {M} }$

Рисунок 1 иллюстрирует влияние метрики при изменении . Два круга показывают множество точек с одинаковым расстоянием до центра . В евклидовом случае это множество представляет собой окружность, тогда как при модифицированной метрике (Махаланобиса) оно становится эллипсоидом . ${\displaystyle \mathbf {M} }$ ${\displaystyle {\vec {x}}_{i}}$

Рисунок 1: Схематическое изображение LMNN.

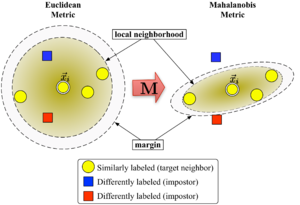
Алгоритм различает два типа специальных точек данных: целевые соседи и самозванцы .

Целевые соседи

Целевые соседи выбираются перед обучением. Каждый экземпляр имеет совершенно разных целевых соседей в пределах , которые все имеют одну и ту же метку класса . Целевые соседи — это точки данных, которые должны стать ближайшими соседями в соответствии с изученной метрикой . Обозначим набор целевых соседей для точки данных как . ${\displaystyle {\vec {x}}_{i}}$ ${\displaystyle k}$ ${\displaystyle D}$ ${\displaystyle y_{i}}$ ${\displaystyle {\vec {x}}_{i}}$ ${\displaystyle N_{i}}$

Самозванцы

Самозванец точки данных — это другая точка данных с другой меткой класса (т.е. ), которая является одним из ближайших соседей . Во время обучения алгоритм пытается минимизировать количество самозванцев для всех экземпляров данных в обучающем наборе. ${\displaystyle {\vec {x}}_{i}}$ ${\displaystyle {\vec {x}}_{j}}$ ${\displaystyle y_{i}\neq y_{j}}$ ${\displaystyle {\vec {x}}_{i}}$

Алгоритм

Large margin neighbors оптимизирует матрицу с помощью полуопределенного программирования . Цель двоякая: для каждой точки данных целевые соседи должны быть близко , а самозванцы должны быть далеко . Рисунок 1 показывает эффект такой оптимизации на наглядном примере. Изученная метрика заставляет входной вектор окружаться обучающими экземплярами того же класса. Если бы это была тестовая точка, она была бы правильно классифицирована по правилу ближайшего соседа. ${\displaystyle \mathbf {M} }$ ${\displaystyle {\vec {x}}_{i}}$ ${\displaystyle {\vec {x}}_{i}}$ ${\displaystyle k=3}$

Первая цель оптимизации достигается путем минимизации среднего расстояния между экземплярами и их целевыми соседями.

${\displaystyle \sum _{i,j\in N_{i}}d({\vec {x}}_{i},{\vec {x}}_{j})}$.

Вторая цель достигается путем штрафования расстояний до самозванцев , которые находятся менее чем на одну единицу дальше, чем целевые соседи (и, следовательно, выталкивают их из локальной окрестности ). Результирующее значение, которое необходимо минимизировать, можно сформулировать как: ${\displaystyle {\vec {x}}_{l}}$ ${\displaystyle {\vec {x}}_{j}}$ ${\displaystyle {\vec {x}}_{i}}$

${\displaystyle \sum _{i,j\in N_{i},l,y_{l}\neq y_{i}}[d({\vec {x}}_{i},{\vec {x}}_{j})+1-d({\vec {x}}_{i},{\vec {x}}_{l})]_{+}}$

С функцией потери шарнира , которая гарантирует, что близость самозванца не штрафуется, когда находится за пределами поля. Поле ровно в одну единицу фиксирует масштаб матрицы . Любой альтернативный выбор приведет к изменению масштаба с коэффициентом . ${\textstyle [\cdot ]_{+}=\max(\cdot ,0)}$ ${\displaystyle M}$ ${\displaystyle c>0}$ ${\displaystyle M}$ ${\displaystyle 1/c}$

Окончательная задача оптимизации принимает вид:

${\displaystyle \min _{\mathbf {M} }\sum _{i,j\in N_{i}}d({\vec {x}}_{i},{\vec {x}}_{j})+\lambda \sum _{i,j,l}\xi _{ijl}}$

${\displaystyle \forall _{i,j\in N_{i},l,y_{l}\neq y_{i}}}$

${\displaystyle d({\vec {x}}_{i},{\vec {x}}_{j})+1-d({\vec {x}}_{i},{\vec {x}}_{l})\leq \xi _{ijl}}$

${\displaystyle \xi _{ijl}\geq 0}$

${\displaystyle \mathbf {M} \succeq 0}$

Гиперпараметр — это некоторая положительная константа (обычно задаваемая через перекрестную проверку). Здесь переменные (вместе с двумя типами ограничений) заменяют член в функции стоимости. Они играют роль, аналогичную переменным слэка , чтобы поглощать степень нарушений ограничений самозванца. Последнее ограничение гарантирует, что является положительно полуопределенным. Задача оптимизации является примером полуопределенного программирования (SDP). Хотя SDP, как правило, страдают от высокой вычислительной сложности, этот конкретный пример SDP может быть решен очень эффективно из-за базовых геометрических свойств задачи. В частности, большинство ограничений самозванца естественным образом удовлетворяются и не нуждаются в принудительном соблюдении во время выполнения (т. е. набор переменных разрежен). Особенно хорошо подходящим методом решения является метод рабочего набора , который сохраняет небольшой набор ограничений, которые активно соблюдаются, и отслеживает оставшиеся (вероятно, удовлетворенные) ограничения только изредка, чтобы гарантировать правильность. ${\textstyle \lambda >0}$ ${\displaystyle \xi _{ijl}}$ ${\displaystyle \mathbf {M} }$ ${\displaystyle \xi _{ijl}}$

Расширения и эффективные решатели

LMNN был расширен на несколько локальных метрик в статье 2008 года. ^[2] Это расширение значительно улучшает ошибку классификации, но включает в себя более затратную задачу оптимизации. В своей публикации 2009 года в Journal of Machine Learning Research ^[3] Вайнбергер и Сол выводят эффективный решатель для полуопределенной программы. Он может выучить метрику для набора рукописных цифр MNIST за несколько часов, включая миллиарды парных ограничений. Реализация Matlab с открытым исходным кодом доступна бесплатно на веб-странице авторов.

Кумал и др. ^[4] расширили алгоритм, включив локальные инвариантности в многомерные полиномиальные преобразования и улучшенную регуляризацию.

Смотрите также

• Обучение на основе сходства
• Линейный дискриминантный анализ
• Изучение векторного квантования
• Псевдометрическое пространство
• Поиск ближайшего соседа
• Кластерный анализ
• Классификация данных
• Сбор данных
• Машинное обучение
• Распознавание образов
• Прогностическая аналитика
• Уменьшение размеров
• Анализ компонентов соседства

Ссылки

1. Weinberger, KQ; Blitzer JC; Saul LK (2006). «Обучение метрике расстояния для классификации ближайших соседей с большим запасом». Достижения в области нейронных систем обработки информации . 18 : 1473–1480.
2. Weinberger, KQ; Saul LK (2008). "Быстрые решатели и эффективные реализации для дистанционного метрического обучения" (PDF) . Труды Международной конференции по машинному обучению : 1160–1167. Архивировано из оригинала (PDF) 2011-07-24 . Получено 2010-07-14 .
3. Вайнбергер, К. К.; Сол Л. К. (2009). «Расстояние метрического обучения для классификации с большим запасом» (PDF) . Журнал исследований машинного обучения . 10 : 207–244.
4. Кумар, MP; Торр PHS; Зиссерман А. (2007). "Инвариантный классификатор ближайшего соседа с большим запасом". 2007 IEEE 11-я Международная конференция по компьютерному зрению . стр. 1–8. doi :10.1109/ICCV.2007.4409041. ISBN 978-1-4244-1630-1. S2CID  1326101.

Внешние ссылки

• Реализация Matlab
• Учебное пособие ICML 2010 по метрическому обучению