Линейный классификатор

В машинном обучении линейный классификатор принимает решение о классификации для каждого объекта на основе линейной комбинации его признаков . Такие классификаторы хорошо подходят для практических задач, таких как классификация документов , и, в более общем плане, для задач со многими переменными ( признаками ), достигая уровней точности, сопоставимых с нелинейными классификаторами, при этом требуя меньше времени на обучение и использование. ^[1]

Определение

Если входной вектор признаков для классификатора является действительным вектором , то выходная оценка равна ${\vec {x}}$

y=f({\vec {w}}\cdot {\vec {x}})=f\left(\sum _{j}w_{j}x_{j}\right),

где — действительный вектор весов, а f — функция, преобразующая скалярное произведение двух векторов в желаемый выходной сигнал. (Другими словами, — это одноформенное или линейное функциональное отображение на R .) Вектор веса изучается на основе набора помеченных обучающих образцов. Часто f — это пороговая функция , которая отображает все значения выше определенного порога в первый класс, а все остальные значения — во второй класс; например, ${\vec {w}}$ ${\vec {w}}$ ${\vec {x}}$ ${\vec {w}}$ ${\vec {w}}\cdot {\vec {x}}$

f(\mathbf {x}) = {\begin{cases}1& {\text{if }} \ \mathbf {w} ^{T} \cdot \mathbf {x} >\theta,\\0& {\text{иначе}}\end{случаи}}

Верхний индекс T указывает на транспонирование и является скалярным порогом. Более сложное f может дать вероятность того, что элемент принадлежит определенному классу. $\тета$

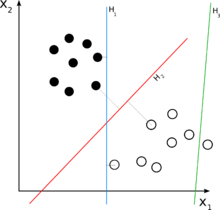
Для задачи двухклассовой классификации работу линейного классификатора можно представить как разбиение многомерного входного пространства гиперплоскостью : все точки на одной стороне гиперплоскости классифицируются как «да», а все остальные — как «нет».

Линейный классификатор часто используется в ситуациях, когда скорость классификации является проблемой, так как он часто является самым быстрым классификатором, особенно когда является разреженным. Кроме того, линейные классификаторы часто работают очень хорошо, когда число измерений в велико, как в классификации документов , где каждый элемент в обычно является числом вхождений слова в документе (см. матрицу документ-термин ). В таких случаях классификатор должен быть хорошо регуляризован . ${\vec {x}}$ ${\vec {x}}$ ${\vec {x}}$

Генеративные модели против дискриминационных моделей

Существует два широких класса методов определения параметров линейного классификатора . Это могут быть генеративные и дискриминационные модели. ^[2]^[3] Методы первого моделируют совместное распределение вероятностей , тогда как методы второго моделируют условные функции плотности . Примерами таких алгоритмов являются: ${\vec {w}}$ $P({\rm {класс}}|{\vec {x}})$

Линейный дискриминантный анализ (ЛДА) — предполагает гауссовские модели условной плотности
Наивный байесовский классификатор с многочленными или многомерными моделями событий Бернулли.

Второй набор методов включает дискриминационные модели , которые пытаются максимизировать качество выходных данных на обучающем наборе . Дополнительные члены в функции стоимости обучения могут легко выполнить регуляризацию окончательной модели. Примеры дискриминационного обучения линейных классификаторов включают:

Логистическая регрессия — оценка максимального правдоподобия, предполагающая, что наблюдаемый обучающий набор был сгенерирован биномиальной моделью, которая зависит от выходных данных классификатора. ${\vec {w}}$
Персептрон — алгоритм, который пытается исправить все ошибки, обнаруженные в обучающем наборе.
Линейный дискриминантный анализ Фишера — алгоритм (отличный от «LDA»), который максимизирует отношение разброса между классами к разбросу внутри класса без каких-либо других предположений. По сути, это метод снижения размерности для бинарной классификации. ^[4]
Машина опорных векторов — алгоритм, который максимизирует разницу между гиперплоскостью решений и примерами в обучающем наборе.

Примечание: несмотря на свое название, LDA не принадлежит к классу дискриминантных моделей в этой таксономии. Однако его название имеет смысл, если мы сравним LDA с другим основным алгоритмом линейного снижения размерности : анализом главных компонент (PCA). LDA — это контролируемый алгоритм обучения , который использует метки данных, в то время как PCA — это неконтролируемый алгоритм обучения , который игнорирует метки. Подводя итог, можно сказать, что название является историческим артефактом. ^[5]

Дискриминационное обучение часто обеспечивает более высокую точность, чем моделирование функций условной плотности ^{[ требуется ссылка ]} . Однако обработка отсутствующих данных часто проще с моделями условной плотности ^{[ требуется ссылка ]} .

Все перечисленные выше линейные алгоритмы классификаторов можно преобразовать в нелинейные алгоритмы, работающие на другом входном пространстве , используя трюк с ядром . $\varphi ({\vec {x}})$

Дискриминационное обучение

Дискриминационное обучение линейных классификаторов обычно происходит контролируемым образом, посредством алгоритма оптимизации , которому дается обучающий набор с желаемыми выходами и функцией потерь , которая измеряет расхождение между выходами классификатора и желаемыми выходами. Таким образом, алгоритм обучения решает задачу оптимизации вида ^[1]

{\underset {\mathbf {w} {\arg \min }}\;R(\mathbf {w})+C\sum _{i=1}^{N}L(y_{i} ,\mathbf {w} ^{\mathsf {T}}\mathbf {x} _{i})

где

$w$ — вектор параметров классификатора,
$L (y i, w T x i)$ — функция потерь, которая измеряет расхождение между прогнозом классификатора и истинным выходом $y i$ для $i$ -го обучающего примера,
$R (w)$ — это функция регуляризации , которая не позволяет параметрам становиться слишком большими (что приводит к переобучению ), и
$C$ — скалярная константа (задается пользователем алгоритма обучения), которая контролирует баланс между регуляризацией и функцией потерь.

Популярные функции потерь включают в себя потерю шарнира (для линейных SVM) и логарифмическую потерю (для линейной логистической регрессии). Если функция регуляризации $R$ является выпуклой , то вышеприведенная задача является выпуклой . ^[1] Существует много алгоритмов для решения таких задач; популярные алгоритмы для линейной классификации включают ( стохастический ) градиентный спуск , L-BFGS , координатный спуск и методы Ньютона .

Смотрите также

Примечания

^ abc Guo-Xun Yuan; Chia-Hua Ho; Chih-Jen Lin (2012). "Последние достижения крупномасштабной линейной классификации" (PDF) . Proc. IEEE . 100 (9). Архивировано (PDF) из оригинала 2017-06-10.
^ Т. Митчелл, Генеративные и дискриминативные классификаторы: наивный байесовский и логистический регресс. Черновая версия, 2005 г.
^ AY Ng и MI Jordan. О дискриминативных и генеративных классификаторах: сравнение логистической регрессии и наивного байесовского алгоритма. в NIPS 14, 2002.
^ RO Duda, PE Hart, DG Stork, «Классификация образов», Wiley, (2001). ISBN 0-471-05669-3
^ Дуда, Ричард О.; Харт, Питер Э.; Сторк, Дэвид Г. (2001). Классификация паттернов . Публикация Wiley-Interscience (Второе издание). Нью-Йорк Чичестер Вайнхайм Брисбен Сингапур Торонто: John Wiley & Sons, Inc. стр. 117. ISBN 978-0-471-05669-0.

Дальнейшее чтение

Y. Yang, X. Liu, «Пересмотр категоризации текста», Proc. ACM SIGIR Conference, стр. 42–49, (1999). paper @ citeseer
Р. Хербрих, «Изучение ядерных классификаторов: теория и алгоритмы», MIT Press, (2001). ISBN 0-262-08306-X