
В машиностроении механизм — это устройство , преобразующее входные силы и движение в желаемый набор выходных сил и движений. Механизмы обычно состоят из движущихся компонентов, которые могут включать в себя шестерни и зубчатые передачи ; ремни и цепные приводы ; кулачки и толкатели ; тяги ; фрикционные устройства, такие как тормоза или сцепления ; структурные компоненты, такие как рама, крепежи, подшипники, пружины или смазочные материалы; различные элементы машин , такие как шлицы, штифты или шпонки.
Немецкий ученый Франц Рёло определяет машину как «комбинацию сопротивляющихся тел, расположенных таким образом, что с их помощью механические силы природы могут быть принуждены совершать работу, сопровождаемую определенным движением». В этом контексте его использование машины обычно трактуется как означающее механизм .
Сочетание силы и движения определяет мощность , а механизм управляет мощностью для достижения желаемого набора сил и движения.
Механизм обычно является частью более крупного процесса, известного как механическая система или машина . Иногда целая машина может называться механизмом; примерами являются рулевой механизм в автомобиле или заводной механизм наручных часов . Однако, как правило, набор из нескольких механизмов называется машиной.
Со времен Архимеда и до эпохи Возрождения механизмы рассматривались как конструкции из простых машин , таких как рычаг , блок , винт , колесо и ось , клин и наклонная плоскость . Рёло сосредоточился на телах, называемых звеньями , и соединениях между этими телами, называемых кинематическими парами или суставами.
Чтобы использовать геометрию для изучения движения механизма, его звенья моделируются как жесткие тела . Это означает, что расстояния между точками в звене предполагаются неизменными при движении механизма, то есть звено не изгибается. Таким образом, относительное движение между точками в двух соединенных звеньях считается результатом кинематической пары, которая их соединяет.
Кинематические пары, или сочленения, считаются обеспечивающими идеальные ограничения между двумя звеньями, такие как ограничение одной точки для чистого вращения или ограничение линии для чистого скольжения, а также чистого качения без проскальзывания и точечного контакта с проскальзыванием. Механизм моделируется как сборка жестких звеньев и кинематических пар.

Рело назвал идеальные соединения между звеньями кинематическими парами . Он различал высшие пары с линейным контактом между двумя звеньями и низшие пары с площадным контактом между звеньями. Дж. Филлипс [ необходимо разъяснение ] показывает, что существует много способов построения пар, которые не соответствуют этой простой модели.
Нижняя пара: Нижняя пара представляет собой идеальное соединение, имеющее поверхностный контакт между парой элементов, как в следующих случаях:
Высшие пары: Как правило, высшая пара — это ограничение, требующее линейного или точечного контакта между элементарными поверхностями. Например, контакт между кулачком и его следящим элементом — это высшая пара, называемая кулачковым соединением . Аналогично, контакт между эвольвентными кривыми, которые образуют зацепляющиеся зубья двух шестерен, — это кулачковые соединения.
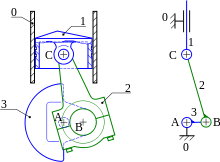
Кинематическая схема сводит компоненты машины к скелетной схеме, которая подчеркивает сочленения и сводит связи к простым геометрическим элементам. Эта схема также может быть сформулирована как граф , представляя связи механизма как ребра, а сочленения как вершины графа. Эта версия кинематической схемы доказала свою эффективность при перечислении кинематических структур в процессе проектирования машины. [1]
Важным фактором в этом процессе проектирования является степень свободы системы связей и шарниров, которая определяется с помощью критерия Чебышева–Грублера–Куцбаха .

Хотя все механизмы в механической системе являются трехмерными, их можно анализировать с помощью плоской геометрии, если движение отдельных компонентов ограничено таким образом, что все траектории точек параллельны или последовательно соединены с плоскостью. В этом случае система называется плоским механизмом . Кинематический анализ плоских механизмов использует подмножество специальной евклидовой группы SE , состоящее из плоских вращений и трансляций, обозначаемых как SE.
Группа SE является трехмерной, что означает, что каждое положение тела на плоскости определяется тремя параметрами. Параметрами часто являются координаты x и y начала координатной системы в M , [ необходимо уточнение ] измеренные от начала координатной системы в F , и угол, измеренный между осью x в F и осью x в M. [ необходимо уточнение ] Это часто описывается как то, что тело на плоскости имеет три степени свободы .
Чистое вращение шарнира и линейное перемещение ползуна можно отнести к подгруппам SE и определить эти два сочленения как сочленения с одной степенью свободы плоских механизмов. [ неразборчиво ] Кулачковое соединение, образованное двумя поверхностями, находящимися в скользящем и вращательном контакте, является сочленением с двумя степенями свободы.

Можно построить механизм таким образом, что траектории точек во всех компонентах лежат в концентрических сферических оболочках вокруг фиксированной точки. Примером является карданный гироскоп . Эти устройства называются сферическими механизмами. [2] Сферические механизмы строятся путем соединения звеньев с шарнирными соединениями таким образом, что оси каждого шарнира проходят через одну и ту же точку. Эта точка становится центром концентрических сферических оболочек. Движение этих механизмов характеризуется группой SO(3) [ необходимо разъяснение ] вращений в трехмерном пространстве. Другими примерами сферических механизмов являются автомобильный дифференциал и роботизированное запястье.
Группа вращения SO(3) является трехмерной. Примером трех параметров, которые определяют пространственное вращение, являются углы крена, тангажа и рыскания, используемые для определения ориентации самолета.
Механизм, в котором тело движется посредством общего пространственного движения, называется пространственным механизмом . Примером является связь RSSR, которую можно рассматривать как четырехзвенную связь, в которой шарнирные соединения соединительного звена заменены концами стержней , также называемыми сферическими соединениями или шаровыми шарнирами . Концы стержней позволяют входным и выходным кривошипам связи RSSR быть смещенными до такой степени, что они лежат в разных плоскостях, что заставляет соединительное звено двигаться в общем пространственном движении. Роботизированные руки , платформы Стюарта и гуманоидные роботизированные системы также являются примерами пространственных механизмов.
Механизм Беннета является примером пространственного сверхограниченного механизма , который состоит из четырех шарнирных соединений.
Группа SE(3) [ необходимо пояснение ] является шестимерной, что означает, что положение тела в пространстве определяется шестью параметрами. Три параметра определяют начало подвижной системы отсчета относительно неподвижной системы. Три других параметра определяют ориентацию подвижной системы отсчета относительно неподвижной системы.

Связь — это набор связей, соединенных шарнирами. Как правило, связи являются структурными элементами, а шарниры обеспечивают движение. Возможно, наиболее полезным примером является плоская четырехзвенная связь . Однако существует еще много специальных связей:
Податливый механизм представляет собой ряд жестких тел, соединенных податливыми элементами. Эти механизмы имеют много преимуществ, включая уменьшенное количество деталей, уменьшенную «люфт» между соединениями (отсутствие паразитного движения из-за зазоров между деталями [3] ), накопление энергии, низкие эксплуатационные расходы (они не требуют смазки и имеют низкий механический износ) и простоту изготовления. [4]
Гибкие подшипники (также известные как гибкие соединения ) представляют собой подкласс податливых механизмов, которые создают геометрически четко определенное движение (вращение) при приложении силы.
Механизм кулачка и толкателя образован прямым контактом двух специально сформированных звеньев. Ведущее звено называется кулачком, а звено, которое приводится в движение посредством прямого контакта их поверхностей, называется толкателем. Форма контактирующих поверхностей кулачка и толкателя определяет движение механизма. В общем случае энергия механизма кулачка и толкателя передается от кулачка к толкателю. Кулачковый вал вращается, и, в соответствии с профилем кулачка, толкатель перемещается вверх и вниз. В настоящее время также доступны несколько иные типы эксцентриковых толкателей кулачка, в которых энергия передается от толкателя к кулачку. Главное преимущество этого типа механизма кулачка и толкателя заключается в том, что толкатель слегка перемещается и помогает вращать кулачок на длину окружности в шесть раз больше с 70% силы.
Передача вращения между соприкасающимися зубчатыми колесами может быть прослежена до Антикитерского механизма в Греции и указывающей на юг колесницы в Китае. Иллюстрации ученого эпохи Возрождения Георгия Агриколы показывают зубчатые передачи с цилиндрическими зубьями. Внедрение эвольвентного зуба дало стандартную конструкцию зубчатой передачи, которая обеспечивает постоянное передаточное отношение. Некоторые важные особенности зубчатых передач и зубчатых передач:
Проектирование механизмов для достижения определенного движения и передачи силы известно как кинематический синтез механизмов . [5] Это набор геометрических методов, которые дают размеры рычажных механизмов, кулачковых и следящих механизмов, а также шестерен и зубчатых передач для выполнения требуемого механического движения и передачи мощности. [6]