
Задача Монти Холла — это головоломка в форме вероятностной головоломки, номинально основанная на американском телевизионном игровом шоу Let's Make a Deal и названная в честь его оригинального ведущего Монти Холла . Задача была первоначально поставлена (и решена) в письме Стива Селвина в American Statistician в 1975 году. [1] [2] Она стала известна как вопрос от читателя Крейга Ф. Уитакера, процитированный в колонке Мэрилин вос Савант «Спросите Мэрилин» в журнале Parade в 1990 году: [3]
Предположим, вы участвуете в игровом шоу, и вам дают на выбор три двери: за одной дверью находится машина, за другими — козы. Вы выбираете дверь, скажем, № 1, и ведущий, который знает, что находится за дверями, открывает другую дверь, скажем, № 3, за которой находится коза. Затем он говорит вам: «Хотите выбрать дверь № 2?» Будет ли вам выгодно изменить свой выбор?
Ответ Саванта состоял в том, что участник должен переключиться на другую дверь. [3] Согласно стандартным предположениям, стратегия переключения имеет 2/3 вероятность выигрыша автомобиля, в то время как стратегия сохранения первоначального выбора имеет только 1/3 вероятность.
Когда игрок впервые делает свой выбор, есть 2/3 вероятность того, что машина находится за одной из невыбранных дверей. Эта вероятность не меняется после того, как ведущий показывает козу за одной из невыбранных дверей. Когда ведущий предоставляет информацию о двух невыбранных дверях (показывая, что за одной из них нет машины), 2/3 вероятность того, что автомобиль находится за одной из невыбранных дверей, зависит от невыбранной и нераскрытой двери, в отличие от 1/3 вероятность того, что автомобиль окажется за дверью, которую участник выбрал изначально.
Данные вероятности зависят от конкретных предположений о том, как ведущий и участник выбирают свои двери. Важное понимание заключается в том, что при этих стандартных условиях имеется больше информации о дверях 2 и 3, чем было доступно в начале игры, когда игрок выбирал дверь 1: действие ведущего добавляет ценность двери, которая не была исключена, но не той, которую изначально выбрал участник. Другое понимание заключается в том, что переключение дверей — это действие, отличное от выбора между двумя оставшимися дверями наугад, поскольку первое действие использует предыдущую информацию, а второе — нет. Другие возможные поведения ведущего, отличные от описанного, могут раскрыть другую дополнительную информацию или вообще ее не раскрыть и дать другие вероятности.
Многие читатели колонки Савант отказались верить в пользу переключения и отвергли ее объяснение. После того, как проблема появилась в Parade , около 10 000 читателей, включая почти 1000 докторов наук , написали в журнал, большинство из них назвали Савант неправой. [4] Даже когда им дали объяснения, симуляции и формальные математические доказательства, многие люди все еще не приняли, что переключение — лучшая стратегия. [5] Пол Эрдёш , один из самых плодовитых математиков в истории, оставался неубежденным, пока ему не показали компьютерную симуляцию, демонстрирующую предсказанный Савант результат. [6]
Проблема является парадоксом истинного типа, поскольку решение настолько контринтуитивно, что может показаться абсурдным, но тем не менее оно очевидно верно. Задача Монти Холла математически тесно связана с более ранней задачей трех заключенных и с гораздо более старым парадоксом ящика Бертрана .
В 1975 году Стив Селвин написал письмо в American Statistician , в котором описал проблему, основанную на игровом шоу Let's Make a Deal , [1] назвав её в последующем письме «проблемой Монти Холла». [2] Математически эта задача эквивалентна задаче о трёх заключённых, описанной в колонке Мартина Гарднера «Математические игры» в журнале Scientific American в 1959 году [7] , и задаче о трёх ракушках, описанной в книге Гарднера « Aha Gotcha» . [8]
По стандартным предположениям вероятность выигрыша автомобиля после переключения составляет 2/3 . Это решение обусловлено поведением хоста. Неоднозначности в версии Parade явно не определяют протокол хоста. Однако решение Мэрилин вос Савант [3], напечатанное рядом с вопросом Уитакера, подразумевает, а Селвин [1] и Савант [5] явно определяют роль хоста следующим образом:
Когда любое из этих предположений изменяется, это может изменить вероятность выигрыша путем переключения дверей, как подробно описано в разделе ниже. Также обычно предполагается, что автомобиль изначально спрятан случайным образом за дверями и что, если игрок изначально выбирает автомобиль, то выбор хозяина, какую дверь, скрывающую козу, открыть, является случайным. [10] Некоторые авторы, независимо или включительно, предполагают, что первоначальный выбор игрока также является случайным. [1]
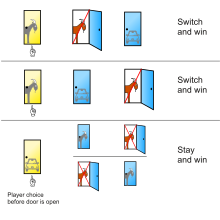
Решение, представленное Савант в Parade, показывает три возможных варианта расположения одной машины и двух коз за тремя дверями, а также результат пребывания или переключения после первоначального выбора двери 1 в каждом случае: [11]
Игрок, который остается с первоначальным выбором, выигрывает только в одном из трех равновероятных вариантов, в то время как игрок, который меняет выбор, выигрывает в двух из трех.
Интуитивное объяснение состоит в том, что если участник изначально выбирает козу (2 из 3 дверей), то он выиграет машину, переключившись, потому что другую козу больше нельзя выбрать — ведущий должен был раскрыть ее местоположение, — тогда как если участник изначально выбирает машину (1 из 3 дверей), то он не выиграет машину, переключившись. [12] Используя стратегию переключения, победа или проигрыш, таким образом, зависят только от того, выбрал ли участник изначально козу ( 2/3 вероятность) или автомобиль ( 1/3 вероятность). Тот факт, что ведущий впоследствии обнаруживает козу в одной из невыбранных дверей, ничего не меняет в первоначальной вероятности. [13]

Большинство людей приходят к выводу, что переключение не имеет значения, поскольку существует 50% вероятность найти машину за любой из двух неоткрытых дверей. Это было бы верно, если бы ведущий выбрал дверь для открытия наугад, но это не так. Дверь, открытая ведущим, зависит от первоначального выбора игрока, поэтому предположение о независимости не выполняется. Перед тем, как ведущий откроет дверь, есть 1/3 вероятность того, что машина находится за каждой дверью. Если машина находится за дверью 1, хост может открыть либо дверь 2, либо дверь 3, поэтому вероятность того, что машина находится за дверью 1 , а хост открывает дверь 3, равна 1/3 × 1/2 = 1/6 . Если машина находится за дверью 2 — а игрок выбрал дверь 1 — ведущий должен открыть дверь 3, то вероятность того, что машина находится за дверью 2 , а ведущий открывает дверь 3, равна 1/3 × 1 = 1/3 . Это единственные случаи, когда ведущий открывает дверь 3, поэтому, если игрок выбрал дверь 1, а ведущий открывает дверь 3, вероятность того, что машина окажется за дверью 2, в два раза выше, чем за дверью 1. Суть в том, что если машина находится за дверью 2, ведущий должен открыть дверь 3, но если машина находится за дверью 1, ведущий может открыть любую дверь.
Другой способ понять решение — рассмотреть вместе две двери, изначально не выбранные игроком. [14] [15] [16] [17] [18] Как выразился Сесил Адамс , [14] «Монти фактически говорит: вы можете сохранить одну дверь или иметь две другие двери». 2/3 шанс найти машину не изменился при открытии одной из этих дверей, потому что Монти, зная местоположение машины, наверняка обнаружит козу. Выбор игрока после того, как ведущий открывает дверь, ничем не отличается от выбора, который ведущий предложил бы игроку переключиться с изначально выбранной двери на набор из двух оставшихся дверей. Переключение в этом случае явно дает игроку 2/3 вероятность выбора автомобиля.
Как говорит Кит Девлин , [15] «Открывая свою дверь, Монти говорит участнику: «Есть две двери, которые ты не выбрал, и вероятность того, что приз находится за одной из них, составляет 2/3 . Я помогу вам, используя свои знания о том, где находится приз, чтобы открыть одну из этих двух дверей, чтобы показать вам, что она не скрывает приз. Теперь вы можете воспользоваться этой дополнительной информацией. Ваш выбор двери A имеет шанс 1 из 3 на победу. Я этого не изменил. Но, исключив дверь C, я показал вам, что вероятность того, что дверь B скрывает приз, составляет 2 из 3. ' "
Савант предполагает, что решение будет более интуитивным с 1 000 000 дверей, а не с 3. [3] В этом случае есть 999 999 дверей с козами за ними и одна дверь с призом. После того, как игрок выбирает дверь, ведущий открывает 999 998 оставшихся дверей. В среднем в 999 999 случаях из 1 000 000 оставшаяся дверь будет содержать приз. Интуитивно игрок должен спросить, насколько вероятно, что, учитывая миллион дверей, ему изначально удалось выбрать правильную. Стибел и др. предположили, что потребность в рабочей памяти подвергается налогообложению во время задачи Монти Холла, и что это заставляет людей «сворачивать» свой выбор в два равновероятных варианта. Они сообщают, что когда количество вариантов увеличивается до более чем 7, люди склонны чаще переключаться; однако большинство участников по-прежнему неверно оценивают вероятность успеха как 50%. [18]
Вы облажались, и облажались по-крупному! Поскольку вам, похоже, трудно уловить основной принцип работы, я объясню. После того, как ведущий показывает козу, у вас теперь есть один шанс из двух оказаться правым. Измените вы свой выбор или нет, шансы одинаковы. В этой стране и так достаточно математической безграмотности, и нам не нужно, чтобы самый высокий в мире IQ распространялся еще больше. Позор!
Скотт Смит, Университет Флориды [3]
Савант написала в своей первой колонке о задаче Монти Холла, что игрок должен переключиться. [3] Она получила тысячи писем от своих читателей — подавляющее большинство из которых, включая многих читателей с докторской степенью, не согласились с ее ответом. В 1990–1991 годах еще три ее колонки в Parade были посвящены этому парадоксу. [19] Многочисленные примеры писем читателей колонок Савант представлены и обсуждены в The Monty Hall Dilemma: A Cognitive Illusion Par Excellence . [20]
Обсуждение было воспроизведено в других местах (например, в газетной колонке Сесила Адамса « The Straight Dope » [14] ) и опубликовано в крупных газетах, таких как The New York Times [4] .
В попытке пояснить свой ответ она предложила проиллюстрировать это игрой в наперстки [8] : «Вы отворачиваетесь, а я кладу горошину под одну из трех ракушек. Затем я прошу вас указать пальцем на ракушку. Вероятность того, что ваш выбор содержит горошину, составляет 1/3 , согласен? Тогда я просто поднимаю пустую ракушку из оставшихся двух. Поскольку я могу (и буду) делать это независимо от того, что вы выбрали, мы не узнали ничего, что позволило бы нам пересмотреть шансы на ракушке под вашим пальцем». Она также предложила похожую симуляцию с тремя игральными картами.
Савант отметила, что, хотя некоторые читатели и не понимали, что им следует исходить из предположения, что ведущий всегда должен показывать козу, почти все ее многочисленные корреспонденты правильно поняли проблемные предположения и поначалу все еще были убеждены, что ответ Савант («переключение») был неверным.
Впервые столкнувшись с задачей Монти Холла, подавляющее большинство людей предположили, что каждая дверь имеет одинаковую вероятность, и пришли к выводу, что переключение не имеет значения. [9] Из 228 испытуемых в одном исследовании только 13% решили переключиться. [21] В своей книге «Сила логического мышления » [22] когнитивный психолог Массимо Пьятелли Пальмарини пишет: «Ни одна другая статистическая головоломка не приближается так близко к тому, чтобы обмануть всех людей все время, [и] даже физики-лауреаты Нобелевской премии систематически дают неправильный ответ, и что они настаивают на этом, и они готовы ругать в печати тех, кто предлагает правильный ответ». Голуби, неоднократно сталкивавшиеся с этой задачей, показывают, что они быстро учатся всегда переключаться, в отличие от людей. [23]
Большинство формулировок проблемы, особенно в Parade , не соответствуют правилам реального игрового шоу [10] и не полностью определяют поведение ведущего или то, что местоположение автомобиля выбирается случайным образом. [21] [4] [24] Однако Краусс и Ванг утверждают, что люди делают стандартные предположения, даже если они явно не указаны. [25]
Хотя эти вопросы математически значимы, даже при учете этих факторов почти все люди по-прежнему думают, что каждая из двух неоткрытых дверей имеет равную вероятность, и приходят к выводу, что переключение не имеет значения. [9] Это предположение о «равной вероятности» является глубоко укоренившейся интуицией. [26] Люди склонны думать, что вероятность равномерно распределена по стольким неизвестным, сколько их есть, независимо от того, есть они или нет. [27]
Проблема продолжает привлекать внимание когнитивных психологов. Типичное поведение большинства, т. е. отсутствие переключения, может быть объяснено явлениями, известными в психологической литературе как:
Экспериментальные данные подтверждают, что это правдоподобные объяснения, которые не зависят от интуиции вероятности. [31] [32] Другая возможность заключается в том, что интуиция людей просто не имеет дела с версией проблемы из учебника, а с реальной обстановкой игрового шоу. [33] Там существует возможность, что ведущий шоу играет обманным путем, открывая другие двери только в том случае, если изначально была выбрана дверь с автомобилем. Ведущий шоу, играющий обманным путем половину раз, изменяет шансы на победу в случае, если кому-то предлагают перейти на «равную вероятность».
Как уже отмечалось, большинство источников по теме вероятности , включая многие вводные учебники по вероятности, решают задачу, показывая, что условные вероятности того, что автомобиль находится за дверью 1 и дверью 2, равны 1/3 и 2/3 (не 1/2 и 1/2 ) при условии, что участник изначально выбирает дверь 1, а ведущий открывает дверь 3; различные способы вывода и интерпретации этого результата были приведены в предыдущих подразделах.
Среди этих источников есть несколько, которые открыто критикуют популярные «простые» решения, заявляя, что эти решения «правильные, но… шаткие» [34] или «не решают поставленную проблему» [35] , или «неполные» [36] , или «неубедительные и вводящие в заблуждение» [37] , или (что наиболее прямолинейно) «ложные» [38] .
Саша Волох (2015) писал, что «любое объяснение, которое говорит что-то вроде «вероятность двери 1 была 1/3 , и ничто не может этого изменить ...' автоматически подозрительно: вероятности являются выражением нашего невежества о мире, и новая информация может изменить степень нашего невежества." [39]
Некоторые говорят, что эти решения отвечают на несколько иной вопрос – одна из формулировок звучит так: «Вы должны объявить до того, как откроется дверь , планируете ли вы перейти на другую услугу» [40] .
Простые решения показывают разными способами, что участник, который настроен на смену, выиграет автомобиль с вероятностью 2/3 , и, следовательно, переключение является выигрышной стратегией, если игрок должен заранее выбрать между «всегда переключаться» и «всегда оставаться». Однако вероятность выигрыша при постоянном переключении — это логически отличная концепция от вероятности выигрыша при переключении, учитывая, что игрок выбрал дверь 1, а ведущий открыл дверь 3. Как говорит один источник, «различие между [этими вопросами], похоже, сбивает с толку многих». [38] Тот факт, что они различны, можно показать, изменив задачу так, чтобы эти две вероятности имели разные числовые значения. Например, предположим, что участник знает, что Монти не открывает вторую дверь случайным образом среди всех законных альтернатив, а вместо этого, когда ему предоставляется возможность выбрать между двумя проигрышными дверями, Монти откроет ту, что справа. В этой ситуации следующие два вопроса имеют разные ответы:
Ответ на первый вопрос: 2/3 , как правильно показано в «простых» решениях. Но ответ на второй вопрос теперь другой: условная вероятность того, что автомобиль находится за дверью 1 или дверью 2, при условии, что хозяин открыл дверь 3 (дверь справа), равна 1/2 . Это потому, что предпочтение Монти крайних правых дверей означает, что он открывает дверь 3, если машина находится за дверью 1 (что изначально с вероятностью 1/3 ) или если автомобиль находится за дверью 2 (также изначально с вероятностью 1/3 ). Для этого варианта два вопроса дают разные ответы. Это отчасти потому, что предполагаемое условие второго вопроса (что ведущий открывает дверь 3) возникнет только в этом варианте с вероятностью 2/3 . Однако, пока начальная вероятность того, что автомобиль находится за каждой дверью, равна 1/3 , смена никогда не будет невыгодной для участника, поскольку условная вероятность победы при смене всегда составляет не менее 1/2 . [38]
В Morgan et al. [ 38] четыре профессора университета опубликовали статью в The American Statistician, утверждая, что Савант дал правильный совет, но неправильный аргумент. Они считали, что вопрос был задан о вероятности того, что машина окажется за дверью 2, учитывая первоначальный выбор игроком двери 1 и открытие хостом игры двери 3, и они показали, что эта вероятность была чем-то средним между 1/2 и 1 в зависимости от процесса принятия решения хостом, учитывая выбор. Только когда решение полностью рандомизировано, шанс 2/3 .
В приглашенном комментарии [41] и в последующих письмах редактору [42] [43] [44] [45] Морган и др. были поддержаны некоторыми авторами, подвергнуты критике другими; в каждом случае ответ Моргана и др. был опубликован вместе с письмом или комментарием в The American Statistician . В частности, Савант яростно защищалась. Морган и др. жаловались в своем ответе Савант [42] , что Савант все еще фактически не ответила на их собственный главный пункт. Позже в своем ответе Хогбину и Нийдаму [45] они согласились, что было бы естественно предположить, что ведущий выбирает дверь для открытия совершенно случайным образом, когда у него есть выбор, и, следовательно, что условная вероятность выигрыша путем переключения (т. е. условная, учитывая ситуацию, в которой находится игрок, когда он должен сделать свой выбор) имеет то же значение, 2/3 , как безусловная вероятность выигрыша путем переключения (т. е. усредненная по всем возможным ситуациям). Это равенство уже подчеркивалось Беллом (1992), который предположил, что математически запутанное решение Моргана и др . будет привлекательно только для статистиков, тогда как эквивалентность условных и безусловных решений в случае симметрии интуитивно очевидна.
В литературе существуют разногласия относительно того, формулировка проблемы Савант, представленная в Parade , задает первый или второй вопрос, и является ли это различие существенным. [46] Берендс заключает, что «нужно тщательно рассмотреть этот вопрос, чтобы увидеть, что оба анализа верны», что не означает, что они одинаковы. [47] Несколько критиков статьи Моргана и др. , [38] чьи вклады были опубликованы вместе с оригинальной статьей, критиковали авторов за изменение формулировки Савант и неверное толкование ее намерения. [46] Один из участников дискуссии (Уильям Белл) посчитал, что это дело вкуса, явно ли упоминать, что (при стандартных условиях) какая дверь открывается хозяином, не зависит от того, следует ли хотеть переключиться.
Среди простых решений «решение с комбинированными дверями» ближе всего к условному решению, как мы видели при обсуждении методов, использующих концепцию шансов и теорему Байеса. Оно основано на глубоко укоренившейся интуиции, что раскрытие уже известной информации не влияет на вероятности . Но знание того, что ведущий может открыть одну из двух невыбранных дверей, чтобы показать козу, не означает, что открытие определенной двери не повлияет на вероятность того, что автомобиль находится за изначально выбранной дверью. Дело в том, что хотя мы заранее знаем, что ведущий откроет дверь и покажет козу, мы не знаем, какую дверь он откроет. Если ведущий выбирает равномерно случайным образом между дверями, скрывающими козу (как это имеет место в стандартной интерпретации), эта вероятность действительно остается неизменной, но если ведущий может выбирать неслучайно между такими дверями, то конкретная дверь, которую открывает ведущий, раскрывает дополнительную информацию. Хозяин всегда может открыть дверь, за которой находится коза , и (в стандартной интерпретации задачи) вероятность того, что машина находится за изначально выбранной дверью, не меняется, но второе верно не из-за первого. Решения, основанные на утверждении, что действия хозяина не могут повлиять на вероятность того, что машина находится за изначально выбранной дверью, кажутся убедительными, но утверждение просто неверно, если только оба выбора хозяина не являются одинаково вероятными, если у него есть выбор. [48] Поэтому утверждение должно быть обосновано; без обоснования решение в лучшем случае неполное. Может быть так, что ответ правильный, но рассуждение, использованное для его обоснования, некорректно.
Простые решения выше показывают, что игрок со стратегией переключения выигрывает автомобиль с общей вероятностью 2/3 , т.е. без учета того, какую дверь открыл хозяин. [49] [13] В соответствии с этим большинство источников по теме вероятности вычисляют условные вероятности того, что автомобиль находится за дверью 1 и дверью 2, как 1/3 и 2/3 соответственно, участник изначально выбирает дверь 1, а ведущий открывает дверь 3. [2] [38] [50] [35] [13] [49] [36] Решения в этом разделе рассматривают только те случаи, в которых игрок выбрал дверь 1, а ведущий открыл дверь 3.
Если предположить, что ведущий открывает дверь наугад, когда ему предоставлен выбор, то то, какую дверь открывает ведущий, не дает нам никакой информации о том, находится ли автомобиль за дверью 1 или нет. В простых решениях мы уже наблюдали, что вероятность того, что автомобиль находится за дверью 1, дверью, изначально выбранной игроком, изначально равна 1/3 . Более того, хозяин наверняка собирается открыть (другую) дверь , поэтому открытие двери ( какой именно — не указано) ничего не меняет. 1/3 должно быть средним значением: вероятности того, что машина находится за дверью 1, учитывая, что хост выбрал дверь 2, и вероятности того, что машина находится за дверью 1, учитывая, что хост выбрал дверь 3: это потому, что это единственные две возможности. Но эти две вероятности одинаковы. Следовательно, они обе равны 1/3 . [38] Это показывает, что вероятность того, что автомобиль находится за дверью 1, учитывая, что игрок изначально выбрал эту дверь и что ведущий открыл дверь 3, составляет 1/3 , и отсюда следует, что вероятность того, что автомобиль находится за дверью 2, учитывая, что игрок изначально выбрал дверь 1, а ведущий открыл дверь 3, составляет 2/3 . Анализ также показывает, что общий уровень успешности 2/3 , достигаемый постоянным переключением , не может быть улучшен и подчеркивает то, что уже могло быть интуитивно очевидным: выбор, стоящий перед игроком, заключается в том, что между изначально выбранной дверью и другой дверью, оставленной хостом закрытой, конкретные числа на этих дверях не имеют значения.

По определению, условная вероятность победы путем переключения, если участник изначально выбирает дверь 1, а ведущий открывает дверь 3, равна вероятности события «машина находится за дверью 2, а ведущий открывает дверь 3», деленной на вероятность «ведущий открывает дверь 3». Эти вероятности можно определить, обратившись к таблице условных вероятностей ниже или к эквивалентному дереву решений . [50] [13] [49] Условная вероятность победы путем переключения равна 1/3/1/3 + 1/6 , который является 2/3 . [2]
Таблица условных вероятностей ниже показывает, как 300 случаев, во всех из которых игрок изначально выбирает дверь 1, будут в среднем разделены в зависимости от местоположения автомобиля и выбора двери, которую должен открыть ведущий.
Во многих учебниках и статьях по теории вероятностей решение условной вероятности выводится посредством формального применения теоремы Байеса ; среди них книги Гилла [51] и Хенце. [52] Использование формы вероятности теоремы Байеса, часто называемой правилом Байеса, делает такой вывод более прозрачным. [34] [53]
Изначально вероятность того, что автомобиль окажется за любой из трех дверей, одинакова: шансы на дверь 1, дверь 2 и дверь 3 составляют 1 : 1 : 1 . Это остается так и после того, как игрок выбрал дверь 1, в силу независимости. Согласно правилу Байеса , апостериорные шансы на местоположение автомобиля, при условии, что хост открывает дверь 3, равны априорным шансам, умноженным на коэффициент Байеса или вероятность, которая по определению является вероятностью новой информации (хост открывает дверь 3) при каждой из рассматриваемых гипотез (местоположение автомобиля). Теперь, поскольку игрок изначально выбрал дверь 1, вероятность того, что хост откроет дверь 3, составляет 50%, если автомобиль находится за дверью 1, 100%, если автомобиль находится за дверью 2, 0%, если автомобиль находится за дверью 3. Таким образом, коэффициент Байеса состоит из соотношений 1/2 : 1 : 0 или, что эквивалентно, 1 : 2 : 0 , в то время как априорные шансы были 1 : 1 : 1 . Таким образом, апостериорные шансы становятся равными байесовскому фактору 1 : 2 : 0 . Учитывая, что хозяин открыл дверь 3, вероятность того, что автомобиль находится за дверью 3, равна нулю, а вероятность того, что он находится за дверью 2, в два раза выше, чем за дверью 1.
Ричард Гилл [54] анализирует вероятность того, что хост откроет дверь 3, следующим образом. Учитывая, что машина не находится за дверью 1, одинаково вероятно, что она находится за дверью 2 или 3. Следовательно, вероятность того, что хост откроет дверь 3, составляет 50%. Учитывая, что машина находится за дверью 1, вероятность того, что хост откроет дверь 3, также составляет 50%, поскольку, когда у хоста есть выбор, любой из вариантов одинаково вероятен. Следовательно, независимо от того, находится ли машина за дверью 1, вероятность того, что хост откроет дверь 3, составляет 50%. Информация «хост открывает дверь 3» вносит фактор Байеса или отношение правдоподобия 1 : 1 относительно того, находится ли машина за дверью 1. Первоначально шансы против того, что дверь 1 скрывает машину, составляли 2 : 1. Следовательно, апостериорные шансы против того, что дверь 1 скрывает машину, остаются такими же, как и априорные шансы, 2 : 1 .
На словах, информация о том, какую дверь открывает хозяин (дверь 2 или дверь 3?), не раскрывает никакой информации о том, находится ли автомобиль за дверью 1, и это именно то, что, как утверждают сторонники простых решений, интуитивно очевидно или, используя идиомы математических доказательств, «очевидно верно, по симметрии». [44]
Возвращаясь к Нейлбаффу, [55] проблема Монти Холла также много изучалась в литературе по теории игр и теории принятия решений , и некоторые популярные решения также соответствуют этой точке зрения. Савант просит решения, а не шанса. И случайные аспекты того, как спрятана машина и как открывается невыбранная дверь, неизвестны. С этой точки зрения, нужно помнить, что у игрока есть две возможности сделать выбор: во-первых, какую дверь выбрать изначально; и, во-вторых, переключаться или нет. Поскольку он не знает, как спрятана машина и как ведущий делает выбор, он может использовать свою возможность первого выбора, как бы нейтрализуя действия команды, проводящей викторину, включая ведущего.
Согласно Гиллу [56] , стратегия участника включает два действия: первоначальный выбор двери и решение переключиться (или остаться), которое может зависеть как от изначально выбранной двери, так и от двери, на которую ведущий предлагает переключиться. Например, стратегия одного участника заключается в том, чтобы «выбрать дверь 1, затем переключиться на дверь 2, когда ее предложат, и не переключаться на дверь 3, когда ее предложат». Существует двенадцать таких детерминированных стратегий участника.
Элементарное сравнение стратегий участников показывает, что для каждой стратегии A существует другая стратегия B «выбрать дверь, а затем переключиться, что бы ни случилось», которая доминирует над ней. [57] Независимо от того, как спрятана машина и какое правило использует ведущий, когда у него есть выбор между двумя козлами, если A выигрывает машину, то и B тоже. Например, стратегия A «выбрать дверь 1, а затем всегда придерживаться ее» доминирует над стратегией B «выбрать дверь 2, а затем всегда переключаться после того, как ведущий открывает дверь»: A выигрывает, когда дверь 1 скрывает машину, в то время как B выигрывает, когда либо дверь 1, либо дверь 3 скрывает машину. Аналогично, стратегия A «выбрать дверь 1, а затем переключиться на дверь 2 (если предлагается), но не переключаться на дверь 3 (если предлагается)» доминирует над стратегией B «выбрать дверь 2, а затем всегда переключаться». A выигрывает, когда дверь 1 скрывает машину, а Монти выбирает открыть дверь 2 или если дверь 3 скрывает машину. Стратегия B выигрывает, когда либо дверь 1, либо дверь 3 скрывает автомобиль, то есть всякий раз, когда выигрывает стратегия A, а также случай, когда дверь 1 скрывает автомобиль, а Монти решает открыть дверь 3.
Доминирование — это веская причина искать решение среди постоянно переключающихся стратегий при довольно общих предположениях об окружающей среде, в которой участник принимает решения. В частности, если автомобиль спрятан с помощью некоторого рандомизирующего устройства — например, бросания симметричного или асимметричного трехгранного кубика — доминирование подразумевает, что стратегия, максимизирующая вероятность выигрыша автомобиля, будет среди трех постоянно переключающихся стратегий, а именно, это будет стратегия, которая изначально выбирает наименее вероятную дверь, а затем переключается независимо от того, какую дверь для переключения предлагает ведущий.
Стратегическое доминирование связывает проблему Монти Холла с теорией игр . В игре с нулевой суммой Гилла [56] отказ от непереключающихся стратегий сводит игру к следующему простому варианту: ведущий (или телевизионная команда) выбирает дверь, за которой будет спрятана машина, а участник выбирает две двери (т. е. две двери, оставшиеся после первого, номинального, выбора игрока). Участник выигрывает (а его противник проигрывает), если машина находится за одной из двух выбранных им дверей.

Простой способ продемонстрировать, что стратегия переключения действительно выигрывает в двух случаях из трех при стандартных предположениях, — это смоделировать игру с игральными картами . [58] [59] Три карты из обычной колоды используются для представления трех дверей; одна «специальная» карта представляет дверь с автомобилем, а две другие карты представляют двери с козой.
Симуляцию можно повторять несколько раз, чтобы имитировать несколько раундов игры. Игрок выбирает одну из трех карт, затем, глядя на оставшиеся две карты, «хозяин» сбрасывает карту козы. Если карта, оставшаяся в руке хозяина, является картой автомобиля, это записывается как выигрыш переключения; если у хозяина в руках карта козы, раунд записывается как оставшийся выигрыш. Поскольку этот эксперимент повторяется в течение нескольких раундов, наблюдаемый процент выигрышей для каждой стратегии, вероятно, приближается к ее теоретической вероятности выигрыша в соответствии с законом больших чисел .
Повторные розыгрыши также проясняют, почему переключение является лучшей стратегией. После того, как игрок выбирает свою карту, уже определено, выиграет ли переключение раунд для игрока. Если это не убедительно, симуляцию можно провести со всей колодой. [58] [14] В этом варианте карта автомобиля переходит к хозяину 51 раз из 52 и остается у хозяина независимо от того, сколько карт, не относящихся к автомобилю, будет сброшено.
Распространенный вариант проблемы, принятый несколькими академическими авторами в качестве канонической проблемы, не делает упрощающего предположения, что ведущий должен единообразно выбирать дверь для открытия, а вместо этого использует какую-то другую стратегию . Путаница относительно того, какая формализация является авторитетной, привела к значительному раздражению, особенно потому, что этот вариант делает доказательства более сложными, не меняя оптимальности стратегии постоянного переключения для игрока. В этом варианте игрок может иметь разные вероятности выигрыша в зависимости от наблюдаемого выбора ведущего, но в любом случае вероятность выигрыша при переключении составляет по крайней мере 1/2 (и может достигать 1), в то время как общая вероятность выигрыша при переключении все еще равна 2/3 . Варианты иногда последовательно излагаются в учебниках и статьях, предназначенных для обучения основам теории вероятностей и теории игр . Также было изучено значительное количество других обобщений.
Версия проблемы Монти Холла, опубликованная в Parade в 1990 году, не утверждала конкретно, что ведущий всегда будет открывать другую дверь, или всегда предлагать выбор для переключения, или даже никогда не открывать дверь, открывающую автомобиль. Однако Савант ясно дала понять в своей второй последующей колонке, что поведение предполагаемого ведущего могло быть только тем, что привело к 2/3 вероятность, которую она дала в качестве своего первоначального ответа. «Все остальное — это другой вопрос». [5] «Практически все мои критики поняли предполагаемый сценарий. Я лично прочитал около трех тысяч писем (из многих дополнительных тысяч, которые пришли) и обнаружил, что почти все они просто настаивали на том, что, поскольку оставалось два варианта (или эквивалентная ошибка), шансы были равны. Очень немногие поднимали вопросы о двусмысленности, и письма, фактически опубликованные в колонке, не были среди этих немногих». [60] Ответ следующий: если автомобиль размещается случайным образом за любой дверью, ведущий должен открыть дверь, открывающую козу, независимо от первоначального выбора игрока, и, если доступны две двери, выбирает, какую из них открыть, случайным образом. [9] В таблице ниже показано множество других возможных вариантов поведения ведущего и влияние на успешность переключения.
Определение лучшей стратегии игрока в рамках заданного набора других правил, которым должен следовать хост, является типом проблемы, изучаемой в теории игр . Например, если хост не обязан делать предложение о смене, игрок может заподозрить, что хост злонамерен и делает предложения чаще, если игрок изначально выбрал автомобиль. В целом, ответ на этот тип вопроса зависит от конкретных предположений, сделанных относительно поведения хоста, и может варьироваться от «полностью игнорировать хоста» до «подбросить монетку и поменяться, если выпадет орел»; см. последнюю строку таблицы ниже.
Морган и др . [38] и Гиллман [35] оба показывают более общее решение, где автомобиль (равномерно) случайно размещается, но ведущий не ограничен в выборе равномерно случайным образом, если игрок изначально выбрал автомобиль, что является тем, как они оба интерпретируют постановку задачи в Parade, несмотря на отказ автора от ответственности. Оба изменили формулировку версии Parade , чтобы подчеркнуть этот момент, когда они переформулировали задачу. Они рассматривают сценарий, в котором ведущий выбирает между раскрытием двух коз с предпочтением, выраженным как вероятность q , имеющая значение от 0 до 1. Если ведущий выбирает случайным образом, q будет 1/2 и переключение выигрывает с вероятностью 2/3 независимо от того, какую дверь открывает хост. Если игрок выбирает дверь 1, а предпочтение хоста двери 3 равно q , то вероятность того, что хост открывает дверь 3, а машина находится за дверью 2, равна 1/3 , в то время как вероятность того, что хозяин откроет дверь 3, а машина окажется за дверью 1, составляет д/3 . Это единственные случаи, когда ведущий открывает дверь 3, поэтому условная вероятность выигрыша при переключении, если ведущий открывает дверь 3, составляет 1/3/1/3 + q /3 что упрощается до 1/1 + д . Поскольку q может изменяться от 0 до 1, эта условная вероятность может изменяться от 1/2 и 1. Это означает, что даже без ограничения хоста на случайный выбор, если игрок изначально выбирает машину, игрок никогда не становится хуже, если переключится. Однако ни один из источников не предполагает, что игрок знает значение q , поэтому игрок не может приписать вероятность, отличную от 2/3 что, по мнению Саванта, было неявным.
DL Ferguson (1975 в письме к Selvin [2] ) предлагает обобщение N -дверей исходной задачи, в которой ведущий открывает p проигрышных дверей, а затем предлагает игроку возможность переключиться; в этом варианте переключение выигрывает с вероятностью . Эта вероятность всегда больше , поэтому переключение всегда приносит преимущество.
Даже если хост открывает только одну дверь ( ), игроку выгоднее переключаться в каждом случае. По мере того, как N становится больше, преимущество уменьшается и приближается к нулю. [64] С другой стороны, если хост открывает все проигрышные двери, кроме одной ( p = N − 2), преимущество увеличивается по мере того, как N становится больше (вероятность выигрыша при переключении составляет Н − 1/Н , который стремится к 1, когда N становится очень большим).
Квантовая версия парадокса иллюстрирует некоторые моменты о связи между классической или неквантовой информацией и квантовой информацией , закодированной в состояниях квантово-механических систем. Формулировка в общих чертах основана на квантовой теории игр . Три двери заменяются квантовой системой, допускающей три альтернативы; открытие двери и взгляд за нее переводятся как выполнение определенного измерения. Правила могут быть изложены на этом языке, и снова выбор игрока заключается в том, чтобы придерживаться первоначального выбора или перейти к другому «ортогональному» варианту. Последняя стратегия, как оказывается, удваивает шансы, как и в классическом случае. Однако, если ведущий шоу не рандомизировал положение приза полностью квантово-механическим способом, игрок может добиться еще большего успеха и иногда даже может выиграть приз с уверенностью. [65] [66]
Самая ранняя из нескольких вероятностных головоломок, связанных с задачей Монти Холла, — это парадокс ящика Бертрана , предложенный Джозефом Бертраном в 1889 году в его «Calcul des probabilités» . [67] В этой головоломке есть три ящика: ящик с двумя золотыми монетами, ящик с двумя серебряными монетами и ящик с одной монетой каждого вида. После выбора ящика наугад и извлечения одной монеты наугад, которая случайно оказывается золотой, возникает вопрос: какова вероятность того, что другая монета будет золотой? Как и в задаче Монти Холла, интуитивный ответ: 1/2 , но вероятность на самом деле 2/3 .
Задача о трех заключенных , опубликованная в колонке «Математические игры » Мартина Гарднера в журнале Scientific American в 1959 году [7] [58], эквивалентна задаче Монти Холла. В этой задаче участвуют три осужденных заключенных, случайный из которых был тайно выбран для помилования. Один из заключенных умоляет надзирателя назвать ему имя одного из других, кого должны казнить, утверждая, что это не раскрывает никакой информации о его собственной судьбе, но увеличивает его шансы на помилование от 1/3 к 1/2 . Надзиратель обязуется (тайно) подбрасывать монетку, чтобы решить, какое имя назвать, если спрашивающий заключенный — тот, кого помилуют. Вопрос в том, изменит ли знание ответа надзирателя шансы заключенного на помилование. Эта задача эквивалентна задаче Монти Холла; у задавшего вопрос заключенного все еще есть 1/3 шанс быть помилованным, но у его неназванного коллеги есть 2/3 шанс.
Стив Селвин сформулировал проблему Монти Холла в паре писем в The American Statistician в 1975 году. [1] [2] В первом письме проблема была представлена в версии, близкой к ее представлению в Parade 15 лет спустя. Второе, по-видимому, является первым использованием термина «проблема Монти Холла». Проблема на самом деле является экстраполяцией из игрового шоу. Монти Холл действительно открыл не ту дверь, чтобы вызвать волнение, но предложил заведомо меньший приз — например, 100 долларов наличными — вместо выбора сменить дверь. Как Монти Холл написал Селвину:
И если вы когда-нибудь попадете на мое шоу, правила для вас остаются неизменными — никаких обменов ящиками после отбора.
— Монти Холл [68]
Версия задачи, очень похожая на ту, что появилась три года спустя в Parade, была опубликована в 1987 году в разделе «Головоломки» журнала The Journal of Economic Perspectives . Нейлбафф, как и более поздние авторы математической экономики, рассматривает задачу как простое и забавное упражнение в теории игр . [55]
«Ловушка Монти Холла», статья Филлипа Мартина 1989 года в Bridge Today , представила проблему Селвина как пример того, что Мартин называет вероятностной ловушкой, когда неслучайная информация рассматривается как случайная, и связала это с концепциями игры в бридж . [69]
Переработанная версия задачи Селвина появилась в колонке вопросов и ответов « Спросите Мэрилин» Мэрилин вос Савант в журнале Parade в сентябре 1990 года. [3] Хотя Савант дала правильный ответ, что переключение победит в двух третях случаев, по ее оценкам, журнал получил 10 000 писем, в том числе около 1000, подписанных докторами наук, многие на бланках математических и естественных факультетов, в которых заявлялось, что ее решение неверно. [4] Из-за подавляющего отклика Parade опубликовал беспрецедентные четыре колонки по этой задаче. [70] В результате огласки задача получила альтернативное название «Мэрилин и козы».
В ноябре 1990 года не менее спорное обсуждение статьи Сэванта состоялось в колонке Сесила Адамса « The Straight Dope ». [14] Адамс изначально ответил, неверно, что шансы для двух оставшихся дверей должны быть один к двум. После того, как читатель написал, чтобы исправить математику анализа Адамса, Адамс согласился, что математически он был неправ. «Вы выбираете дверь № 1. Теперь вам предлагается выбор: открыть дверь № 1 или открыть дверь № 2 и дверь № 3. В последнем случае вы сохраняете приз, если он находится за любой из дверей. Вы бы предпочли иметь два шанса из трех на приз, чем один из трех, не так ли? Если вы подумаете об этом, исходная задача предлагает вам по сути тот же выбор. Монти говорит по сути: вы можете сохранить свою одну дверь или вы можете иметь другие две двери, одну из которых (не призовую дверь) я открою для вас». Адамс сказал, что версия Parade оставила критические ограничения неуказанными, и без этих ограничений шансы на победу при переключении не обязательно составляли два из трех (например, было бы неразумно предполагать, что ведущий всегда открывает дверь). Однако многочисленные читатели написали, утверждая, что Адамс был «прав с первого раза» и что правильные шансы были один из двух.
Колонка Parade и ее ответ привлекли значительное внимание прессы, включая статью на первой странице The New York Times, в которой сам Монти Холл дал интервью. [4] Холл понял проблему, проведя репортеру демонстрацию с ключами от машины и объяснив, как реальный игровой процесс в Let's Make a Deal отличается от правил головоломки. В статье Холл указал, что, поскольку он контролировал ход игры, играя на психологии участника, теоретическое решение не применялось к реальному игровому процессу шоу. Он сказал, что его не удивило настойчивое утверждение экспертов о том, что вероятность составляет 1 из 2. «Точно такое же предположение сделали бы участники шоу после того, как я показал бы им, что за одной дверью ничего нет», — сказал он. «Они бы подумали, что шансы на их дверь теперь возросли до 1 из 2, поэтому они не хотели бы отдавать дверь, сколько бы денег я ни предлагал. Открывая эту дверь, мы оказывали давление. Мы называли это обработкой Генри Джеймса . Это было « Поворот винта ». Холл пояснил, что как ведущий игрового шоу он не обязан следовать правилам головоломки в колонке Savant и не всегда должен давать человеку возможность переключиться (например, он может немедленно открыть дверь, если это проигрышная дверь, может предложить им деньги, чтобы они не переключались с проигрышной двери на выигрышную, или может разрешить им возможность переключиться только в том случае, если у них есть выигрышная дверь). «Если ведущий должен все время открывать дверь и предлагать вам переключиться, то вам следует воспользоваться этим переключением», — сказал он. «Но если у него есть выбор, разрешить переключение или нет, будьте осторожны. Caveat emptor. Все зависит от его настроения».
Роман Эндрю Круми «Мистер Ми» (2000) содержит версию проблемы Монти Холла, поставленную в 18 веке. В главе 1 она представлена как игра в наперстки, в которой заключенный должен выиграть, чтобы спасти свою жизнь. В главе 8 философ Розье, его студент Тиссо и жена Тиссо проверяют вероятности с помощью моделирования и проверяют контринтуитивный результат. Затем они проводят эксперимент с черными и белыми бусинами, напоминающий парадокс мальчика или девочки , и в юмористическом намеке на парадокс Эйнштейна-Подольского-Розена Розье ошибочно заключает, что «как только я увидел свою собственную бусинку, волна чистой вероятности мгновенно пролетела с одного конца комнаты на другой. Это объясняет внезапное изменение с двух третей до половины, поскольку конечный квант вероятности (весом одна шестая) чудесным образом прошел между бусинами, запущенный моим собственным актом наблюдения». [71] Розье объясняет свою теорию Тиссо, но «Его плохое понимание моих теорий проявилось несколько дней спустя, когда его сестра собиралась родить, и Тиссо заплатил за то, чтобы в комнату отправили девочку, полагая, что это увеличит вероятность рождения нового ребенка мальчиком в два раза. Однако мой ученик получил племянницу; и я без труда объяснил ошибочность его рассуждений. Тиссо просто неправильно понял мой замечательный парадокс близнецов, который гласит, что если мальчик говорит вам, что у него есть брат или сестра, то вероятность того, что это сестра, составляет не половину, а две трети». [72] Далее следует версия неожиданного парадокса подвешивания .
В главе 101 книги Марка Хэддона «Загадочное ночное происшествие с собакой» (2003) рассказчик Кристофер обсуждает проблему Монти Холла, описывая ее историю и решение. Он заключает: «И это показывает, что интуиция иногда может ошибаться. И интуиция — это то, что люди используют в жизни для принятия решений. Но логика может помочь вам найти правильный ответ». [73]
{{cite journal}}: CS1 maint: постскриптум ( ссылка ){{cite web}}: CS1 maint: постскриптум ( ссылка ){{cite journal}}: CS1 maint: дата и год ( ссылка )