Тест перестановки

Точная статистическая проверка гипотезы

Тест перестановки (также называемый тестом повторной рандомизации или тестом перестановки) — это точный статистический тест гипотезы, использующий доказательство от противного . Тест перестановки включает в себя два или более образца. Нулевая гипотеза заключается в том, что все образцы происходят из одного и того же распределения . При нулевой гипотезе распределение статистики теста получается путем вычисления всех возможных значений статистики теста при возможных перестановках наблюдаемых данных. Таким образом, тесты перестановки являются формой повторной выборки . ${\displaystyle H_{0}:F=G}$

Тесты перестановок можно понимать как тестирование суррогатных данных , где суррогатные данные при нулевой гипотезе получаются посредством перестановок исходных данных. ^[1]

Другими словами, метод, с помощью которого лечение назначается субъектам в экспериментальном проекте, отражается в анализе этого проекта. Если метки взаимозаменяемы при нулевой гипотезе, то полученные тесты дают точные уровни значимости; см. также взаимозаменяемость . Затем из тестов можно вывести доверительные интервалы. Теория развилась из работ Рональда Фишера и Э. Дж. Г. Питмана в 1930-х годах.

Тесты перестановки не следует путать с рандомизированными тестами . ^[2]

Метод

Анимация вычисления теста перестановки на наборах из 4 и 5 случайных значений. 4 значения, выделенные красным, взяты из одного распределения, а 5 значений, выделенные синим, — из другого; мы хотели бы проверить, различаются ли средние значения двух распределений. Гипотеза заключается в том, что среднее значение первого распределения выше среднего значения второго; нулевая гипотеза заключается в том, что обе группы выборок взяты из одного и того же распределения. Существует 126 различных способов поместить 4 значения в одну группу и 5 в другую (9-выберите-4 или 9-выберите-5). Из них один соответствует исходной маркировке, а остальные 125 являются «перестановками», которые генерируют показанную гистограмму средних разностей. P-значение гипотезы оценивается как доля перестановок, которые дают разницу, такую ​​же большую или большую, чем разница средних значений исходных выборок. В этом примере нулевая гипотеза не может быть отклонена на уровне p = 5% . ${\displaystyle {\hat {\mu }}_{1}-{\hat {\mu }}_{2}}$

Чтобы проиллюстрировать основную идею теста перестановки, предположим, что мы собираем случайные величины и для каждого человека из двух групп и чьи выборочные средние значения и , и что мы хотим узнать, происходят ли и из одного и того же распределения. Пусть и будет размером выборки, собранной из каждой группы. Тест перестановки предназначен для определения того, достаточно ли велика наблюдаемая разница между выборочными средними значениями, чтобы отвергнуть на некотором уровне значимости нулевую гипотезу H о том, что данные, взятые из , принадлежат к тому же распределению, что и данные, взятые из . ${\displaystyle X_{A}}$ ${\displaystyle X_{B}}$ ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle {\bar {x}}_{A}}$ ${\displaystyle {\bar {x}}_{B}}$ ${\displaystyle X_{A}}$ ${\displaystyle X_{B}}$ ${\displaystyle n_{A}}$ ${\displaystyle n_{B}}$ ${\displaystyle _{0}}$ ${\displaystyle A}$ ${\displaystyle B}$

Тест выполняется следующим образом. Сначала вычисляется разница в средних значениях между двумя выборками: это наблюдаемое значение тестовой статистики, . ${\displaystyle T_{\text{obs}}}$

Затем наблюдения групп и объединяются, и вычисляется и регистрируется разница в средних значениях выборки для каждого возможного способа разделения объединенных значений на две группы размером и (т. е. для каждой перестановки групповых меток A и B). Набор этих вычисленных разностей представляет собой точное распределение возможных разностей (для этой выборки) при нулевой гипотезе о том, что групповые метки взаимозаменяемы (т. е. назначаются случайным образом). ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle n_{A}}$ ${\displaystyle n_{B}}$

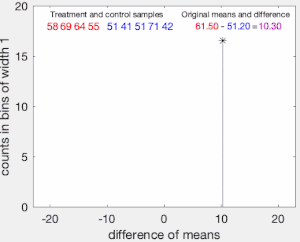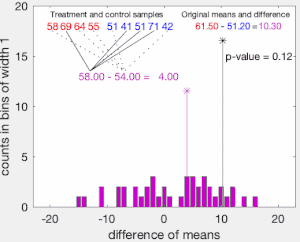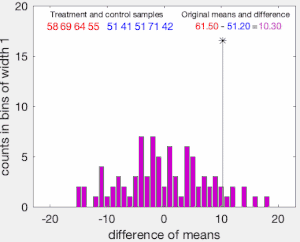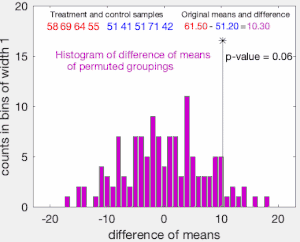
Одностороннее p-значение теста вычисляется как доля выборочных перестановок, где разница в средних значениях была больше . Двустороннее p-значение теста вычисляется как доля выборочных перестановок, где абсолютная разница была больше . Многие реализации тестов перестановок требуют, чтобы сами наблюдаемые данные учитывались как одна из перестановок, так что p-значение перестановки никогда не будет равно нулю. ^[3] ${\displaystyle T_{\text{obs}}}$ ${\displaystyle |T_{\text{obs}}|}$

В качестве альтернативы, если единственной целью теста является отклонение или неотклонение нулевой гипотезы, можно отсортировать записанные различия, а затем наблюдать, содержится ли в среднем % из них, для некоторого уровня значимости . Если это не так, мы отвергаем гипотезу об идентичных кривых вероятности на уровне значимости. ${\displaystyle T_{\text{obs}}}$ ${\displaystyle (1-\alpha )\times 100}$ ${\displaystyle \alpha }$ ${\displaystyle \alpha \times 100\%}$

Чтобы использовать снижение дисперсии с помощью парных выборок, необходимо применить парный тест перестановки, см. парный тест разности .

Отношение к параметрическим тестам

Тесты перестановки являются подмножеством непараметрической статистики . Предполагая, что наши экспериментальные данные получены из данных, измеренных в двух группах лечения, метод просто генерирует распределение средних различий при предположении, что две группы не различаются с точки зрения измеряемой переменной. Из этого затем используют наблюдаемую статистику ( выше), чтобы увидеть, в какой степени эта статистика является специальной, т. е. вероятность наблюдения величины такого значения (или большего), если метки лечения были просто рандомизированы после лечения. ${\displaystyle T_{\text{obs}}}$

В отличие от тестов перестановки, распределения, лежащие в основе многих популярных «классических» статистических тестов, таких как t -тест , F -тест , z -тест и χ2 ^- тест , получены из теоретических распределений вероятностей . Точный тест Фишера является примером широко используемого параметрического теста для оценки связи между двумя дихотомическими переменными. Когда размеры выборки очень велики, тест хи-квадрат Пирсона даст точные результаты. Для небольших выборок нельзя предположить, что эталонное распределение хи-квадрат даст правильное описание распределения вероятностей тестовой статистики, и в этой ситуации использование точного теста Фишера становится более уместным.

Тесты перестановки существуют во многих ситуациях, когда параметрические тесты не существуют (например, при выводе оптимального теста, когда потери пропорциональны размеру ошибки, а не ее квадрату). Все простые и многие относительно сложные параметрические тесты имеют соответствующую версию теста перестановки, которая определяется с использованием той же тестовой статистики, что и параметрический тест, но получает p-значение из распределения перестановки этой статистики, специфичного для выборки, а не из теоретического распределения, полученного из параметрического предположения. Например, таким образом можно построить тест перестановки t , тест перестановки ассоциации, версию теста Эли для перестановки для сравнения дисперсий и т. д. ${\textstyle \chi ^{2}}$

Главные недостатки тестов перестановок заключаются в том, что они

• Может быть вычислительно интенсивным и может потребовать "пользовательский" код для трудновычисляемой статистики. Это должно быть переписано для каждого случая.
• В первую очередь используются для получения p-значения. Инверсия теста для получения доверительных областей/интервалов требует еще больше вычислений.

Преимущества

Тесты перестановки существуют для любой тестовой статистики, независимо от того, известно ли ее распределение. Таким образом, всегда можно выбрать статистику, которая наилучшим образом различает гипотезу и альтернативу и которая минимизирует потери.

Тесты перестановки могут использоваться для анализа несбалансированных конструкций ^[4] и для объединения зависимых тестов на смесях категориальных, порядковых и метрических данных (Pesarin, 2001) ^{[ требуется ссылка ]} . Их также можно использовать для анализа качественных данных, которые были квантифицированы (т. е. превращены в числа). Тесты перестановки могут быть идеальными для анализа квантифицированных данных, которые не удовлетворяют статистическим предположениям, лежащим в основе традиционных параметрических тестов (например, t-тестов, ANOVA), ^[5] см. PERMANOVA .

До 1980-х годов задача создания эталонного распределения была непосильной, за исключением наборов данных с небольшими размерами выборки.

С 1980-х годов слияние относительно недорогих быстрых компьютеров и разработка новых сложных алгоритмов пути, применимых в особых ситуациях, сделали применение методов перестановочного теста практичным для широкого круга задач. Это также инициировало добавление опций точного теста в основные статистические программные пакеты и появление специализированного программного обеспечения для выполнения широкого спектра одно- и многомерных точных тестов и вычисления «точных» доверительных интервалов на основе тестов.

Ограничения

Важное предположение, лежащее в основе теста перестановки, заключается в том, что наблюдения взаимозаменяемы при нулевой гипотезе. Важным следствием этого предположения является то, что тесты на разницу в местоположении (например, тест перестановки t) требуют равной дисперсии при предположении нормальности. В этом отношении классический тест перестановки t имеет ту же слабость, что и классический тест Стьюдента ( проблема Беренса–Фишера ). Это можно решить тем же способом, которым классический тест t был расширен для обработки неравных дисперсий: путем использования статистики Уэлча с поправкой Саттертуэйта на степени свободы. ^[6] Третьей альтернативой в этой ситуации является использование теста на основе бутстрапа. Статистик Филипп Гуд объясняет разницу между тестами перестановки и тестами бутстрапа следующим образом: «Перестановки проверяют гипотезы, касающиеся распределений; бутстрапы проверяют гипотезы, касающиеся параметров. В результате бутстрап влечет за собой менее строгие предположения». ^[7] Тесты бутстрапа не являются точными. В некоторых случаях тест перестановки, основанный на надлежащим образом стьюдентизированной статистике, может быть асимптотически точным, даже если предположение о взаимозаменяемости нарушается. ^[8] Тесты на основе бутстрепа могут тестировать с нулевой гипотезой и, следовательно, подходят для выполнения тестирования эквивалентности . ${\displaystyle H_{0}:F\neq G}$

Тестирование Монте-Карло

Асимптотически эквивалентный тест перестановки может быть создан, когда существует слишком много возможных упорядочений данных, чтобы обеспечить полный подсчет удобным способом. Это делается путем генерации эталонного распределения с помощью выборки Монте-Карло , которая берет небольшую (относительно общего числа перестановок) случайную выборку возможных повторений. Осознание того, что это может быть применено к любому тесту перестановки на любом наборе данных, стало важным прорывом в области прикладной статистики. Самые ранние известные ссылки на этот подход - Иден и Йейтс (1933) и Дуосс (1957). ^{[9] [10]} Этот тип теста перестановки известен под разными названиями: тест приближенной перестановки , тесты перестановки Монте-Карло или тесты случайной перестановки . ^[11]

После случайных перестановок можно получить доверительный интервал для p-значения на основе биномиального распределения, см. Доверительный интервал биномиальной пропорции . Например, если после случайных перестановок p-значение оценивается как , то 99% доверительный интервал для истинного (того, который получился бы в результате перебора всех возможных перестановок) составляет . ${\displaystyle N}$ ${\displaystyle N=10000}$ ${\displaystyle {\widehat {p}}=0.05}$ ${\displaystyle p}$ ${\displaystyle \left[{\hat {p}}-z{\sqrt {\frac {0.05(1-0.05)}{10000}}},{\hat {p}}+z{\sqrt {\frac {0.05(1-0.05)}{10000}}}\right]=[0.045,0.055]}$

С другой стороны, цель оценки p-значения чаще всего состоит в том, чтобы решить , , где порог, при котором нулевая гипотеза будет отклонена (обычно ). В приведенном выше примере доверительный интервал говорит нам только о том, что существует примерно 50% вероятность того, что p-значение будет меньше 0,05, т. е. совершенно неясно, следует ли отклонять нулевую гипотезу на уровне . ${\displaystyle p\leq \alpha }$ ${\displaystyle \scriptstyle \ \alpha }$ ${\displaystyle \alpha =0.05}$ ${\displaystyle \alpha =0.05}$

Если важно только знать, для заданного , логично продолжать моделирование до тех пор, пока утверждение не будет установлено как истинное или ложное с очень низкой вероятностью ошибки. Учитывая ограничение допустимой вероятности ошибки (вероятности обнаружения того, что на самом деле или наоборот), вопрос о том, сколько перестановок генерировать, можно рассматривать как вопрос о том, когда прекратить генерировать перестановки, основываясь на результатах моделирования до сих пор, чтобы гарантировать, что вывод (который является либо , либо ) является правильным с вероятностью, по крайней мере, такой же большой, как . ( обычно будет выбираться крайне малым, например, 1/1000.) Были разработаны правила остановки для достижения этого ^[12] , которые могут быть включены с минимальными дополнительными вычислительными затратами. Фактически, в зависимости от истинного базового p-значения часто будет обнаруживаться, что количество требуемых симуляций чрезвычайно мало (например, всего 5 и часто не больше 100), прежде чем решение может быть принято с виртуальной уверенностью. ${\displaystyle p\leq \alpha }$ ${\displaystyle \alpha }$ ${\displaystyle p\leq \alpha }$ ${\displaystyle \epsilon }$ ${\displaystyle {\widehat {p}}>\alpha }$ ${\displaystyle p\leq \alpha }$ ${\displaystyle p\leq \alpha }$ ${\displaystyle p>\alpha }$ ${\displaystyle 1-\epsilon }$ ${\displaystyle \epsilon }$

Примеры тестов

• Пермутационный дисперсионный анализ
• Рейтинг продукта

Смотрите также

• Ранговый тест
• тест Лепажа

Литература

Оригинальные ссылки:

• Фишер, Р.А. (1935) Планирование экспериментов , Нью-Йорк: Hafner
• Питман, Э. Дж. Г. (1937) «Тесты значимости, которые могут применяться к выборкам из любой популяции», Приложение Королевского статистического общества , 4: 119–130 и 225–32 (части I и II). JSTOR  2984124 JSTOR  2983647
• Питман, Э. Дж. Г. (1938). «Тесты значимости, которые могут быть применены к образцам из любой популяции. Часть III. Тест дисперсионного анализа». Biometrika . 29 (3–4): 322–335. doi :10.1093/biomet/29.3-4.322.

Современные ссылки:

• Коллингридж, Д.С. (2013). «Учебник по количественному анализу данных и тестированию перестановок». Журнал исследований смешанных методов . 7 (1): 79–95. doi :10.1177/1558689812454457. S2CID  124618343.
• Эджингтон, Э.С. и Онгена, П. (2007) Рандомизационные тесты , 4-е изд. Нью-Йорк: Chapman and Hall/CRC ISBN 9780367577711 
• Гуд, Филлип И. (2005) Перестановочные, параметрические и бутстрап-тесты гипотез , 3-е изд., Springer ISBN 0-387-98898-X 
• Good, P (2002). «Расширения концепции взаимозаменяемости и их применение». Журнал современных прикладных статистических методов . 1 (2): 243–247. doi : 10.22237/jmasm/1036110240 .
• Луннеборг, Клифф. (1999) Анализ данных методом повторной выборки , Duxbury Press. ISBN 0-534-22110-6 . 
• Песарин, Ф. (2001). Тесты многомерной перестановки: с приложениями в биостатистике , John Wiley & Sons . ISBN 978-0471496700 
• Уэлч, У. Дж. (1990). «Построение тестов перестановок». Журнал Американской статистической ассоциации . 85 (411): 693–698. doi :10.1080/01621459.1990.10474929.

Методы расчета:

• Мехта, CR; Патель, NR (1983). «Сетевой алгоритм для выполнения точного теста Фишера в таблицах сопряженности rxc». Журнал Американской статистической ассоциации . 78 (382): 427–434. doi :10.1080/01621459.1983.10477989.
• Мехта, CR; Патель, NR; Сенчаудхури, П. (1988). «Выборка по важности для оценки точных вероятностей в выводе перестановок». Журнал Американской статистической ассоциации . 83 (404): 999–1005. doi :10.1080/01621459.1988.10478691.
• Gill, PMW (2007). "Эффективное вычисление p-значений в линейно-статистических тестах значимости перестановок" (PDF) . Журнал статистических вычислений и моделирования . 77 (1): 55–61. CiteSeerX  10.1.1.708.1957 . doi :10.1080/10629360500108053. S2CID  1813706.

Текущие исследования тестов перестановок

• Гуд, ПИ (2012) Практическое руководство по методам повторной выборки.
• Гуд, ПИ (2005) Пермутационные, параметрические и бутстрап-тесты гипотез
• Хестерберг, TC, Д.С. Мур, С. Монаган, А. Клипсон и Р. Эпштейн (2005): Методы бутстрапа и тесты перестановок, программное обеспечение.
• Мур, Д.С., Г. МакКейб, В. Дакворт и С. Сков (2003): Методы бутстрапа и тесты перестановок
• Саймон, Дж. Л. (1997): Повторная выборка: новая статистика.
• Ю, Чонг Хо (2003): Методы повторной выборки: концепции, приложения и обоснование. Практическая оценка, исследования и оценка, 8(19). (статистический бутстраппинг)
• Повторная выборка: союз компьютеров и статистики (ERIC Digests)
• Песарин, Ф., Сальмасо, Л. (2010). Тесты перестановок для сложных данных: теория, приложения и программное обеспечение. Wiley. https://books.google.com/books?id=9PWVTOanxPUC&hl=de

Ссылки

1. Мур, Джейсон Х. «Бутстреппинг, тестирование перестановок и метод суррогатных данных». Физика в медицине и биологии 44.6 (1999): L11.
2. Онгена, Патрик (2017-10-30), Бергер, Вэнс В. (ред.), «Тесты рандомизации или тесты перестановки? Историческое и терминологическое разъяснение», Рандомизация, маскирование и сокрытие распределения (1-е изд.), Бока-Ратон, Флорида: Chapman and Hall/CRC, стр. 209–228, doi :10.1201/9781315305110-14, ISBN 978-1-315-30511-0, получено 2021-10-08
3. Phipson, Belinda; Smyth, Gordon K (2010). «Permutation p-values ​​should never be zero:calculation exact p-values ​​when permutations are randomly drawed». Статистические приложения в генетике и молекулярной биологии . 9 (1): Статья 39. arXiv : 1603.05766 . doi : 10.2202/1544-6115.1585. PMID  21044043. S2CID  10735784.
4. "Invited Articles" (PDF) . Журнал современных прикладных статистических методов . 1 (2): 202–522. Осень 2011 г. Архивировано из оригинала (PDF) 5 мая 2003 г.
5. Коллингридж, Дэйв С. (11 сентября 2012 г.). «Учебник по количественному анализу данных и тестированию перестановок». Журнал исследований смешанных методов . 7 (1): 81–97. doi :10.1177/1558689812454457. S2CID  124618343.
6. Янссен, Арнольд (1997). «Стьюдентизированные перестановочные тесты для не-Iid гипотез и обобщенная проблема Беренса-Фишера». Statistics & Probability Letters . 36 (1): 9–21. doi :10.1016/s0167-7152(97)00043-6.
7. Good, Phillip I. (2005). Методы повторной выборки: практическое руководство по анализу данных (3-е изд.). Birkhäuser. ISBN 978-0817643867.
8. Chung, EY; Romano, JP (2013). «Точные и асимптотически надежные тесты перестановок». Анналы статистики . 41 (2): 487–507. arXiv : 1304.5939 . doi : 10.1214/13-AOS1090 .
9. Иден, Т; Йейтс, Ф (1933). «О валидности z-теста Фишера при его применении к реальному примеру ненормальных данных. (С пятью текстовыми рисунками.)». Журнал сельскохозяйственной науки . 23 (1): 6–17. doi :10.1017/S0021859600052862. S2CID  84802682. Получено 3 июня 2021 г.
10. Дуасс, Мейер (1957). «Модифицированные рандомизационные тесты для непараметрических гипотез». Annals of Mathematical Statistics . 28 (1): 181–187. doi : 10.1214/aoms/1177707045 . JSTOR  2237031.
11. Томас Э. Николс , Эндрю П. Холмс (2001). «Непараметрические тесты перестановок для функциональной нейровизуализации: учебник с примерами» (PDF) . Картирование человеческого мозга . 15 (1): 1–25. doi :10.1002/hbm.1058. hdl :2027.42/35194. PMC 6871862. PMID  11747097 . 
12. Ганди, Аксель (2009). «Последовательная реализация тестов Монте-Карло с равномерно ограниченным риском повторной выборки». Журнал Американской статистической ассоциации . 104 (488): 1504–1511. arXiv : math/0612488 . doi : 10.1198/jasa.2009.tm08368. S2CID  15935787.