Префиксная сумма

Последовательность в информатике

В информатике префиксная сумма , накопительная сумма , инклюзивное сканирование или просто сканирование последовательности чисел x ₀ , x ₁ , x ₂ ,... представляет собой вторую последовательность чисел y ₀ , y ₁ , y ₂ , . .. суммы префиксов ( промежуточных итогов ) входной последовательности :

у ₀ = х ₀

у ₁ = х ₀ + х ₁

у ₂ = х ₀ + х ₁ + х ₂

...

Например, префиксные суммы натуральных чисел представляют собой треугольные числа :

Префиксные суммы легко вычислить в последовательных моделях вычислений, используя формулу y _i = y _{i - 1} + x _i для вычисления каждого выходного значения в порядке последовательности. Однако, несмотря на простоту вычисления, суммы префиксов являются полезным примитивом в некоторых алгоритмах, таких как подсчет сортировки , ^{[1] [2]} , и они составляют основу функции сканирования высшего порядка в языках функционального программирования . Префиксные суммы также широко изучались в параллельных алгоритмах , как в качестве тестовой задачи, которую необходимо решить, так и в качестве полезного примитива, который можно использовать в качестве подпрограммы в других параллельных алгоритмах. ^{[3] [4] [5]}

Абстрактно, для префиксной суммы требуется только бинарный ассоциативный оператор ⊕ , что делает его полезным для многих приложений, от вычисления хорошо разделенных парных разложений точек до обработки строк. ^{[6] [7]}

Математически операцию взятия префиксных сумм можно обобщить от конечных до бесконечных последовательностей; в этом контексте префиксная сумма известна как частичная сумма ряда . Префиксное суммирование или частичное суммирование образуют линейные операторы в векторных пространствах конечных или бесконечных последовательностей; их обратные являются конечно-разностными операторами.

Сканирование функции высшего порядка

В терминах функционального программирования префиксная сумма может быть обобщена на любую двоичную операцию (а не только на операцию сложения ); функция более высокого порядка, возникающая в результате этого обобщения, называется сканированием и тесно связана с операцией сгиба . Операции сканирования и свертывания применяют данную бинарную операцию к одной и той же последовательности значений, но отличаются тем, что сканирование возвращает всю последовательность результатов бинарной операции, тогда как свертывание возвращает только окончательный результат. Например, последовательность факториалов чисел может быть сгенерирована путем сканирования натуральных чисел с использованием умножения вместо сложения:

Инклюзивные и эксклюзивные сканы

Язык программирования и библиотечная реализация сканирования могут быть как инклюзивными , так и исключительными . Инклюзивное сканирование включает входные данные x _i при вычислении выходных данных y _i (т. е. ), тогда как эксклюзивное сканирование не включает (т. е. ). В последнем случае реализации либо оставляют y ₀ неопределенным, либо принимают отдельное значение « x ₋₁ » для заполнения сканирования. Любой тип сканирования можно преобразовать в другой: инклюзивное сканирование можно преобразовать в эксклюзивное сканирование, сдвинув массив, созданный в результате сканирования, вправо на один элемент и вставив значение идентификатора слева от массива. И наоборот, исключающее сканирование можно преобразовать в инклюзивное сканирование путем сдвига массива, созданного в результате сканирования, влево и вставки суммы последнего элемента сканирования и последнего элемента входного массива справа от массива. ^[8] ${\textstyle y_{i}=\bigoplus _{j=0}^{i}x_{j}}$ ${\textstyle y_{i}=\bigoplus _{j=0}^{i-1}x_{j}}$

В следующей таблице приведены примеры инклюзивных и эксклюзивных функций сканирования, предоставляемых несколькими языками программирования и библиотеками:

Модель параллельного программирования OpenMP на основе директив поддерживает как инклюзивную, так и исключительную поддержку сканирования, начиная с версии 5.0.

Параллельные алгоритмы

Существует два ключевых алгоритма параллельного вычисления суммы префиксов. Первый предлагает более короткий интервал и больший параллелизм , но неэффективен в работе. Второй вариант более эффективен, но требует удвоенного диапазона и обеспечивает меньший параллелизм. Они представлены по очереди ниже.

Алгоритм 1: короче пролет, больше параллельности

Схематическое представление суммы параллельных префиксов с 16 входами и высокой степенью параллелизма.

Хиллис и Стил представляют следующий параллельный алгоритм суммирования префиксов: ^[9]

для  i <- 0 до пола (log 2 ( n )) делать  для  j <- 0 до n - 1 делать параллельно,  если  j < 2 i  , то  xя +1 
Дж<- хя 
Дж еще  хя +1 
Дж<- хя 
Дж+ хя 
j - 2 я

Вышеупомянутое обозначение означает значение j -го элемента массива x на временном шаге i . ${\displaystyle x_{j}^{i}}$

На одном процессоре этот алгоритм будет выполняться за время O ( n log n ) . Однако если машина имеет как минимум n процессоров для параллельного выполнения внутреннего цикла, алгоритм в целом выполняется за время O (log n ) , количество итераций внешнего цикла.

Алгоритм 2: Эффективный

Схематическое представление эффективной суммы параллельных префиксов с 16 входами

Эффективную сумму параллельных префиксов можно вычислить с помощью следующих шагов. ^{[3] [10] [11]}

1. Вычислите суммы последовательных пар элементов, в которых первый элемент пары имеет четный индекс: z ₀ = x ₀ + x ₁ , z ₁ = x ₂ + x ₃ и т. д.
2. Рекурсивно вычислить префиксную сумму w ₀ , w ₁ , w ₂ , ... последовательности z ₀ , z ₁ , z ₂ , ...
3. Выразите каждый член конечной последовательности y ₀ , y ₁ , y ₂ , ... как сумму до двух членов этих промежуточных последовательностей: y ₀ = x ₀ , y ₁ = z ₀ , y ₂ = z ₀ + x ₂ , y ₃ = w ₁ и т. д. После первого значения каждое последующее число y _i либо копируется из позиции, находящейся в половине последовательности w , либо предыдущее значение добавляется к одному значению в последовательности x .

Если входная последовательность имеет n шагов, то рекурсия продолжается до глубины O (log n ) , что также является ограничением времени параллельного выполнения этого алгоритма. Число шагов алгоритма равно O ( n ) , и его можно реализовать на параллельной машине произвольного доступа с O ( n /log n ) процессорами без какого-либо асимптотического замедления путем назначения нескольких индексов каждому процессору в раундах алгоритма для в которых элементов больше, чем процессоров. ^[3]

Обсуждение

Каждый из предыдущих алгоритмов выполняется за время O (log n ) . Однако в первом случае требуется ровно log ₂ n шагов, а во втором — 2 log ₂  n − 2 шага. Для проиллюстрированных примеров с 16 входами Алгоритм 1 является 12-канальным параллельным (49 единиц работы, разделенным на интервал 4), тогда как Алгоритм 2 является только 4-канальным параллельным (26 единиц работы, разделенными на 6). Однако алгоритм 2 эффективен по работе — он выполняет только постоянный коэффициент (2) от объема работы, требуемой последовательным алгоритмом, — в то время как алгоритм 1 неэффективен по работе — он выполняет асимптотически больше работы (логарифмический коэффициент), чем требуется. последовательно. Следовательно, алгоритм 1, вероятно, будет работать лучше, когда доступен обильный параллелизм, но алгоритм 2, вероятно, будет работать лучше, когда параллелизм более ограничен.

Параллельные алгоритмы для сумм префиксов часто можно обобщить на другие операции сканирования ассоциативных двоичных операций ^{[3] [4]} , а также их можно эффективно вычислять на современном параллельном оборудовании, таком как графический процессор . ^[12] Идея встроить в аппаратуру функциональный блок, предназначенный для вычисления многопараметрической префикс-суммы, была запатентована Узи Вишкиным . ^[13]

Многие параллельные реализации используют двухпроходную процедуру, при которой частичные суммы префиксов вычисляются при первом проходе на каждом процессоре; затем вычисляется префиксная сумма этих частичных сумм и передается обратно в процессоры для второго прохода с использованием теперь известного префикса в качестве начального значения. Асимптотически этот метод требует примерно двух операций чтения и одной операции записи на элемент.

Конкретные реализации алгоритмов суммы префиксов

Реализация параллельного алгоритма суммирования префиксов, как и других параллельных алгоритмов, должна учитывать архитектуру распараллеливания платформы. Более конкретно, существует множество алгоритмов, адаптированных для платформ, работающих с общей памятью, а также алгоритмов, которые хорошо подходят для платформ, использующих распределенную память , полагающихся на передачу сообщений как на единственную форму межпроцессного взаимодействия.

Общая память: двухуровневый алгоритм

Следующий алгоритм предполагает модель машины с общей памятью ; все обрабатывающие элементы (PE) имеют доступ к одной и той же памяти. Версия этого алгоритма реализована в Многоядерной стандартной библиотеке шаблонов (MCSTL), ^{[14] [15]} — параллельной реализации стандартной библиотеки шаблонов C++ , которая предоставляет адаптированные версии для параллельных вычислений различных алгоритмов.

Чтобы одновременно вычислять сумму префиксов по элементам данных с элементами обработки, данные разбиваются на блоки, каждый из которых содержит элементы (для простоты мы предполагаем, что делит ). Обратите внимание: хотя алгоритм делит данные на блоки, параллельно одновременно выполняются только элементы обработки. ${\displaystyle n}$ ${\displaystyle p}$ ${\displaystyle p+1}$ ${\displaystyle {\frac {n}{p+1}}}$ ${\displaystyle p+1}$ ${\displaystyle n}$ ${\displaystyle p+1}$ ${\displaystyle p}$

При первом проходе каждый PE вычисляет сумму локальных префиксов для своего блока. Последний блок вычислять не требуется, поскольку эти суммы префиксов рассчитываются только как смещения к суммам префиксов последующих блоков, а последний блок по определению не является успешным.

Смещения , хранящиеся в последней позиции каждого блока, накапливаются в виде собственной суммы префиксов и сохраняются в последующих позициях. Для небольшого числа это быстрее делать последовательно, для большого этот шаг можно выполнить и параллельно. ${\displaystyle p}$ ${\displaystyle p}$ ${\displaystyle p}$

Выполняется вторая развертка. На этот раз первый блок обрабатывать не нужно, поскольку не требуется учитывать смещение предыдущего блока. Однако в этот цикл вместо этого включается последний блок, и суммы префиксов для каждого блока вычисляются с учетом смещений блоков суммы префиксов, вычисленных в предыдущем цикле.

function prefix_sum ( elements ) { n := размер ( elements ) p := количество обрабатывающих элементов prefix_sum : = [ 0. . .0 ] размера n делать параллельно i = 0 to p - 1 { // i := индекс текущего PE от j = i * n / ( p + 1 ) до ( i + 1 ) * n / ( p + 1 ) - 1 do { // Здесь сохраняется только префиксная сумма локальных блоков store_prefix_sum_with_offset_in ( elements , 0 , prefix_sum ) } } x = 0 for i = 1 to p { // Последовательное накопление общей суммы блоков x += prefix_sum [ i * n / ( p + 1 ) - 1 ] // Построение суммы префикса для первых p блоков prefix_sum [ i * n / ( p + 1 )] = x // Сохранение результатов для использования в качестве смещений во втором развертка } do Parallel i = 1 to p { // i := индекс текущего PE от j = i * n / ( p + 1 ) до ( i + 1 ) * n / ( p + 1 ) - 1 do { offset := prefix_sum [ i * n / ( p + 1 )] // Вычисляем сумму префикса, принимая сумму предыдущих блоков в качестве смещения                                                                                                                        store_prefix_sum_with_offset_in ( элементы , смещение , prefix_sum ) } } return prefix_sum }       

Улучшение: в случае, если количество блоков слишком велико, что делает последовательный шаг трудоемким из-за развертывания одного процессора, для ускорения второго этапа можно использовать алгоритм Хиллиса и Стила.

Распределенная память: алгоритм Hypercube

Алгоритм суммирования префиксов Hypercube ^[16] хорошо адаптирован для платформ с распределенной памятью и работает с обменом сообщениями между элементами обработки. Предполагается, что в алгоритме участвуют процессорные элементы (PE), равные числу углов в -мерном гиперкубе . ${\displaystyle p=2^{d}}$ ${\displaystyle d}$

Разные гиперкубы для разного количества узлов.

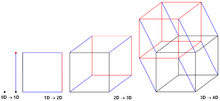
На протяжении всего алгоритма каждый PE рассматривается как угол гипотетического гиперкуба со знанием общей суммы префиксов, а также префиксной суммы всех элементов до себя (в соответствии с упорядоченными индексами среди PE), как в своем собственном гиперкуб. ${\displaystyle \sigma }$ ${\displaystyle x}$

• Алгоритм начинается с предположения, что каждый PE является единственным углом нульмерного гиперкуба и, следовательно , равен сумме локальных префиксов своих собственных элементов. ${\displaystyle \sigma }$ ${\displaystyle x}$
• Алгоритм продолжает объединение гиперкубов, смежных по одному измерению. Во время каждого объединения происходит обмен и агрегирование между двумя гиперкубами, что сохраняет инвариант, заключающийся в том, что все PE в углах этого нового гиперкуба хранят общую сумму префиксов этого вновь объединенного гиперкуба в своей переменной . Однако только гиперкуб, содержащий PE с более высоким индексом, также добавляет это к своей локальной переменной , сохраняя инвариант, который хранит только значение префиксной суммы всех элементов в PE с индексами, меньшими или равными их собственному индексу. ${\displaystyle \sigma }$ ${\displaystyle \sigma }$ ${\displaystyle \sigma }$ ${\displaystyle x}$ ${\displaystyle x}$

В -мерном гиперкубе с PE в углах алгоритм необходимо повторить несколько раз, чтобы нульмерные гиперкубы были объединены в одномерный гиперкуб. Предполагая дуплексную модель связи , в которой два соседних PE в разных гиперкубах могут обмениваться данными в обоих направлениях за один шаг связи, это означает запуски связи. ${\displaystyle d}$ ${\displaystyle 2^{d}}$ ${\displaystyle d}$ ${\displaystyle 2^{d}}$ ${\displaystyle d}$ ${\displaystyle \sigma }$ ${\displaystyle d=\log _{2}p}$

i : = Индекс собственного процессорного элемента ( PE ) m : = префиксная сумма локальных элементов этого PE d : = количество измерений гиперкуба _ _ _ _                        х знак равно м ; // Инвариант: префиксная сумма до этого PE в текущем субкубе σ = m ; // Инвариант: префиксная сумма всех элементов в текущем подкубе      for ( k = 0 ; k <= d - 1 ; k ++ ) { y = σ @ PE ( i xor 2 ^ k ) // Получаем общую сумму префиксов противоположного подкуба по измерению k σ = σ + y // Агрегируем префиксную сумму обоих субкубов                     if ( i & 2 ^ k ) { x = x + y // Агрегируем только сумму префикса из другого субкуба, если этот PE имеет более высокий индекс. } }           

Большие размеры сообщений: конвейерное двоичное дерево

Алгоритм конвейерного двоичного дерева ^[17] — еще один алгоритм для платформ с распределенной памятью, который особенно хорошо подходит для сообщений большого размера.

Как и алгоритм гиперкуба, он предполагает особую структуру связи. Элементы обработки (PE) гипотетически расположены в виде двоичного дерева (например, дерева Фибоначчи) с инфиксной нумерацией в соответствии с их индексом внутри PE. Связь в таком дереве всегда происходит между родительскими и дочерними узлами.

Инфиксная нумерация гарантирует, что для любого заданного PE _j индексы всех узлов, достижимых его левым поддеревом, меньше , а индексы всех узлов в правом поддереве больше . Индекс родительского элемента больше любого из индексов в поддереве PE _{j , если PE j} является левым дочерним элементом, и меньше, если PE _j является правым дочерним элементом. Это позволяет сделать следующие рассуждения: ${\displaystyle \mathbb {[l...j-1]} }$ ${\displaystyle j}$ ${\displaystyle \mathbb {[j+1...r]} }$ ${\displaystyle j}$

Обмен информацией между обрабатывающими элементами во время восходящей (синий) и нисходящей (красный) фаз в алгоритме конвейерной суммы префиксов двоичного дерева.

• Сумма локальных префиксов левого поддерева должна быть агрегирована для вычисления суммы локальных префиксов PE _j . ${\displaystyle \mathbb {\oplus [l..j-1]} }$ ${\displaystyle \mathbb {\oplus [l..j]} }$
• Сумма локальных префиксов правого поддерева должна быть агрегирована для вычисления суммы локальных префиксов PE _h более высокого уровня , которые достигаются на пути, содержащем левое дочернее соединение (что означает ). ${\displaystyle \mathbb {\oplus [j+1..r]} }$ ${\displaystyle h>j}$
• Общая сумма префиксов PE _j необходима для расчета общих сумм префиксов в правом поддереве (например, для узла с самым высоким индексом в поддереве). ${\displaystyle \mathbb {\oplus [0..j]} }$ ${\displaystyle \mathbb {\oplus [0..j..r]} }$
• PE _j должен включать общую сумму префиксов первого узла более высокого порядка, который достигается по восходящему пути, включая правое дочернее соединение, для расчета его общей суммы префиксов. ${\displaystyle \mathbb {\oplus [0..l-1]} }$

Обратите внимание на различие между локальными и общими префиксными суммами поддерева. Пункты два, три и четыре могут привести к мысли, что они образуют круговую зависимость, но это не так. PE более низкого уровня могут потребовать общую сумму префиксов PE более высокого уровня для расчета общей суммы префиксов, но PE более высокого уровня требуют только суммы локальных префиксов поддерева для расчета общей суммы префиксов. Корневому узлу как узлу самого высокого уровня требуется только сумма локальных префиксов его левого поддерева для вычисления собственной суммы префиксов. Каждому PE на пути от PE ₀ до корня PE требуется только сумма локальных префиксов его левого поддерева для вычисления собственной суммы префиксов, тогда как каждому узлу на пути от PE _p-1 (последний PE) до _корня PE требуется общая сумма префикса своего родителя для расчета собственной общей суммы префикса.

Это приводит к двухфазному алгоритму:

Восходящая фаза
Распространяет сумму локального префикса поддерева на его родительский элемент для каждого PE _j . ${\displaystyle \mathbb {\oplus [l..j..r]} }$

Нисходящая фаза.
Распространение эксклюзивной (эксклюзивной PE _j, а также PE в его левом поддереве) общей суммы префиксов всех PE с более низким индексом, которые не включены в адресуемое поддерево PE _j , на PE более низкого уровня в левом дочернем поддереве PE _j. . Распространите сумму инклюзивного префикса на правое дочернее поддерево PE _j . ${\displaystyle \mathbb {\oplus [0..l-1]} }$ ${\displaystyle \mathbb {\oplus [0..j]} }$

Обратите внимание, что алгоритм выполняется параллельно на каждом PE, и PE будут блокироваться при получении до тех пор, пока их дети/родители не предоставят им пакеты.

k := количество пакетов в сообщении m PE m @ { left , right , родительский , this } : = // Сообщения на разных PE                  х = м @ это    // Фаза восходящего движения — вычисление сумм локальных префиксов поддерева для j = 0 до k — 1 : // Конвейерная обработка: для каждого пакета сообщения if hasLeftChild : блокировка приема m [ j ] @ left // Это заменяет локальный m[j] с полученным m[j] // Агрегируем инклюзивную сумму локального префикса из PE с меньшим индексом x [ j ] = m [ j ] ⨁ x [ j ]                   if hasRightChild : блокировка получения m [ j ] @ right // Мы не агрегируем m[j] в сумму локального префикса, поскольку правые дочерние элементы имеют PE с более высоким индексом send x [ j ] ⨁ m [ j ] родительскому элементу else : send x [ j ] родительскому _                  // Нисходящая фаза для j = 0 до k - 1 : m [ j ] @ this = 0         if hasParent : блокировка получения m [ j ] @ родитель // Для левого дочернего элемента m[j] — это сумма эксклюзивного префикса родителей, для правого дочернего элемента — сумма инклюзивного префикса x [ j ] = m [ j ] ⨁ x [ j ] send m [ j ] влево // Общая сумма префиксов всех PE, меньших или равных этому PE, или любого PE в левом поддереве send x [ j ] вправо // Общая сумма префиксов всех PE, меньших или равных этому PE                        

Конвейерная обработка

Если сообщение m длины n можно разделить на k пакетов и оператор ⨁ можно использовать для каждого из соответствующих пакетов сообщений отдельно, конвейерная обработка возможна. ^[17]

Если алгоритм используется без конвейерной обработки, всегда работают только два уровня (отправляющий PE и принимающий PE) двоичного дерева, пока все остальные PE находятся в режиме ожидания. Если имеется p элементов обработки и используется сбалансированное двоичное дерево, то дерево имеет уровни, поэтому длина пути от до равна максимальному количеству непараллельных коммуникационных операций во время восходящей фазы, а также коммуникация на нисходящей фазе. путь также ограничен стартапами. Предполагая, что время запуска связи и время побайтовой передачи , восходящая и нисходящая фазы ограничены в неконвейерном сценарии. ${\displaystyle \log _{2}p}$ ${\displaystyle PE_{0}}$ ${\displaystyle PE_{\mathbb {root} }}$ ${\displaystyle \log _{2}p-1}$ ${\displaystyle \log _{2}p-1}$ ${\displaystyle T_{\mathbb {start} }}$ ${\displaystyle T_{\mathbb {byte} }}$ ${\displaystyle (2\log _{2}p-2)(T_{\mathbb {start} }+n\cdot T_{\mathbb {byte} })}$

После разделения на k пакетов, каждый из которых имеет размер , и отправки их отдельно первый пакет все равно необходимо передать как часть суммы локального префикса, и это произойдет снова для последнего пакета, если . Однако между ними все PE на пути могут работать параллельно, и каждая третья операция связи (получение слева, получение справа, отправка родительскому устройству) отправляет пакет на следующий уровень, так что одна фаза может быть завершена в операциях связи и необходимы обе фазы вместе , что благоприятно для больших размеров сообщений n . ${\displaystyle {\tfrac {n}{k}}}$ ${\displaystyle (\log _{2}p-1)\left(T_{\mathbb {start} }+{\frac {n}{k}}\cdot T_{\mathbb {byte} }\right)}$ ${\displaystyle PE_{\mathbb {root} }}$ ${\displaystyle k>\log _{2}p}$ ${\displaystyle 2\log _{2}p-1+3(k-1)}$ ${\displaystyle (4\cdot \log _{2}p-2+6(k-1))\left(T_{\mathbb {start} }+{\frac {n}{k}}\cdot T_{\mathbb {byte} }\right)}$

Алгоритм может быть дополнительно оптимизирован за счет использования полнодуплексной или телефонной модели связи и перекрытия восходящей и нисходящей фаз. ^[17]

Структуры данных

Когда набор данных может обновляться динамически, он может храниться в древовидной структуре данных Фенвика . Эта структура позволяет как искать любое отдельное значение суммы префикса, так и изменять любое значение массива за логарифмическое время за операцию. ^[18] Однако в более ранней статье 1982 года ^[19] представлена ​​структура данных, называемая деревом частичных сумм (см. раздел 5.1), которая, по-видимому, перекрывает деревья Фенвика; в 1982 году термин «префикс-сумма» еще не был так распространен, как сегодня.

Для массивов более высокой размерности таблица суммированных площадей предоставляет структуру данных, основанную на суммах префиксов, для вычисления сумм произвольных прямоугольных подмассивов. Это может быть полезным примитивом в операциях свертки изображений . ^[20]

Приложения

Сортировка по подсчету — это алгоритм сортировки целых чисел , который использует префиксную сумму гистограммы частот ключей для вычисления положения каждого ключа в отсортированном выходном массиве. Он выполняется за линейное время для целочисленных ключей, меньших количества элементов, и часто используется как часть поразрядной сортировки — быстрого алгоритма сортировки целых чисел, величина которых менее ограничена. ^[1]

Ранжирование списка , проблема преобразования связанного списка в массив , представляющий одну и ту же последовательность элементов, можно рассматривать как вычисление суммы префикса в последовательности 1, 1, 1,... и последующее сопоставление каждого элемента с позицией массива. задается значением суммы префикса; комбинируя ранжирование списков, суммы префиксов и циклы Эйлера , многие важные проблемы с деревьями могут быть решены с помощью эффективных параллельных алгоритмов. ^[4]

Раннее применение параллельных алгоритмов суммирования префиксов было при разработке двоичных сумматоров , логических схем, которые могут складывать два n -битных двоичных числа. В этом приложении последовательность битов переноса сложения может быть представлена ​​как операция сканирования последовательности пар входных битов с использованием функции большинства для объединения предыдущего переноса с этими двумя битами. Затем каждый бит выходного номера можно найти как исключительный или из двух входных битов с соответствующим битом переноса. Используя схему, выполняющую операции параллельного алгоритма суммирования префиксов, можно спроектировать сумматор, использующий O ( n ) логические элементы и O (log n ) временных шагов. ^{[3] [10] [11]}

В модели вычислений с параллельными машинами с произвольным доступом суммы префиксов могут использоваться для моделирования параллельных алгоритмов, которые предполагают возможность одновременного доступа нескольких процессоров к одной и той же ячейке памяти на параллельных машинах, которые запрещают одновременный доступ. С помощью сортировочной сети набор запросов параллельного доступа к памяти можно упорядочить в последовательность так, чтобы доступы к одной и той же ячейке были непрерывными внутри последовательности; Затем операции сканирования можно использовать для определения того, какие из обращений успешны в записи в запрошенные ячейки, а также для распределения результатов операций чтения памяти по нескольким процессорам, которые запрашивают один и тот же результат. ^[21]

В докторской диссертации Гая Беллоха. В диссертации ^[22] параллельные префиксные операции являются частью формализации модели параллелизма данных , предоставляемой такими машинами, как Connection Machine . Соединительная машина CM-1 и CM-2 обеспечивала гиперкубическую сеть, в которой мог быть реализован описанный выше алгоритм 1, тогда как CM-5 предоставляла выделенную сеть для реализации алгоритма 2. ^[23]

При построении кодов Грея , последовательностей двоичных значений со свойством, что последовательные значения последовательности отличаются друг от друга в одной битовой позиции, число n можно преобразовать в значение кода Грея в позиции n последовательности, просто взяв исключительный или из n и n /2 (число, образованное сдвигом n вправо на одну битовую позицию). Обратная операция, декодирование значения x в коде Грея в двоичное число, более сложна, но может быть выражена как префиксная сумма битов  x , где каждая операция суммирования внутри суммы префикса выполняется по модулю два. Префиксная сумма этого типа может быть эффективно выполнена с использованием поразрядных логических операций, доступных на современных компьютерах, путем вычисления исключающего числа x с каждым из чисел, образованных сдвигом x влево на количество битов, равное степени двойки. . ^[24]

Параллельный префикс (с использованием умножения в качестве базовой ассоциативной операции) также можно использовать для построения быстрых алгоритмов параллельной полиномиальной интерполяции . В частности, его можно использовать для вычисления коэффициентов разделенной разности формы Ньютона интерполяционного полинома. ^[25] Этот подход, основанный на префиксах, также может использоваться для получения обобщенных разделенных разностей для (сливной) интерполяции Эрмита , а также для параллельных алгоритмов для систем Вандермонда . ^[26]

Смотрите также

• Вычисления общего назначения на графических процессорах
• Сегментированное сканирование
• Таблица суммированных площадей

Рекомендации

1. Кормен, Томас Х .; Лейзерсон, Чарльз Э .; Ривест, Рональд Л .; Штейн, Клиффорд (2001), «Сортировка подсчетом 8.2», Введение в алгоритмы (2-е изд.), MIT Press и McGraw-Hill , стр. 168–170, ISBN 0-262-03293-7.
2. Коул, Ричард; Вишкин, Узи (1986), «Детерминистическое подбрасывание монеты с применением оптимального ранжирования параллельных списков», Information and Control , 70 (1): 32–53, doi : 10.1016/S0019-9958(86)80023-7
3. Ladner, RE; Фишер, MJ (1980), «Параллельное вычисление префиксов», Journal of the ACM , 27 (4): 831–838, CiteSeerX 10.1.1.106.6247 , doi : 10.1145/322217.322232, MR  0594702, S2CID  207568668 .
4. Тарьян, Роберт Э .; Вишкин, Узи (1985), «Эффективный параллельный алгоритм двусвязности», SIAM Journal on Computing , 14 (4): 862–874, CiteSeerX 10.1.1.465.8898 , doi : 10.1137/0214061 .
5. Лакшмиварахан, С.; Дхалл, СК (1994), Параллелизм в проблеме префиксов , Oxford University Press , ISBN 0-19508849-2.
6. Блеллох, Гай (2011), Суммы префиксов и их приложения (конспекты лекций) (PDF) , Университет Карнеги-Меллона.
7. Каллахан, Пол; Косараджу, С. Рао (1995), «Разложение многомерных наборов точек с применением к потенциальным полям k-ближайших соседей и n-тел», Journal of the ACM , 42 (1): 67–90, doi : 10.1145/200836.200853 , S2CID  1818562.
8. "GPU Gems 3" .
9. Хиллис, В. Дэниел; Стил-младший, Гай Л. (декабрь 1986 г.). «Алгоритмы параллельного анализа данных». Коммуникации АКМ . 29 (12): 1170–1183. дои : 10.1145/7902.7903 .
10. Офман, Ю. (1962), Об алгоритмической сложности строительных работ, Доклады Академии наук СССР , 145 (1): 48–51, МР  0168423. Английский перевод, «Об алгоритмической сложности дискретных функций», Доклады физики СССР 7 : 589–591, 1963.
11. Храпченко, В.М. (1967), "Асимптотическая оценка времени сложения параллельного сумматора", Проблемы Кибернета. (на русском языке), 19 : 107–122.. Английский перевод в Сист. Теория Рез. 19 ; 105–122, 1970.
12. Сенгупта, Шубхабрата; Харрис, Марк; Чжан, Яо; Оуэнс, Джон Д. (2007). Сканирование примитивов для вычислений на графическом процессоре. Учеб. 22-й симпозиум ACM SIGGRAPH/EUROGRAPHICS по графическому оборудованию. стр. 97–106. Архивировано из оригинала 3 сентября 2014 г. Проверено 29 ноября 2007 г.
13. Вишкин, Узи (2003). Префиксные суммы и их применение. Патент США 6542918.
14. Синглер, Йоханнес. «MCSTL: Библиотека стандартных шаблонов многоядерных процессоров» . Проверено 29 марта 2019 г.
15. Синглер, Йоханнес; Сандерс, Питер; Путце, Феликс (2007). «MCSTL: Многоядерная стандартная библиотека шаблонов». Euro-Par 2007 Параллельная обработка . Конспекты лекций по информатике. Том. 4641. стр. 682–694. дои : 10.1007/978-3-540-74466-5_72. ISBN 978-3-540-74465-8. ISSN  0302-9743.
16. Анант Грама; Випин Кумар; Аншул Гупта (2003). Введение в параллельные вычисления. Аддисон-Уэсли. стр. 85, 86. ISBN. 978-0-201-64865-2.
17. Сандерс, Питер; Трефф, Йеспер Ларссон (2006). «Алгоритмы параллельного префикса (сканирования) для MPI». Последние достижения в области параллельных виртуальных машин и интерфейса передачи сообщений . Конспекты лекций по информатике. Том. 4192. стр. 49–57. дои : 10.1007/11846802_15. ISBN 978-3-540-39110-4. ISSN  0302-9743.
18. Фенвик, Питер М. (1994), «Новая структура данных для кумулятивных таблиц частот», Software: Practice and Experience , 24 (3): 327–336, doi : 10.1002/spe.4380240306, S2CID  7519761
19. Шилоах, Йоси; Вишкин, Узи (1982b), «О ( n 2 ^log  n  ) параллельный алгоритм максимального потока», Journal of Algorithms , 3 (2): 128–146, doi : 10.1016/0196-6774(82)90013-X
20. Селиски, Ричард (2010), «Таблица суммированных площадей (интегральное изображение)», Компьютерное зрение: алгоритмы и приложения, Тексты по информатике, Springer, стр. 106–107, ISBN 9781848829350.
21. Вишкин, Узи (1983), «Реализация одновременного доступа к адресам памяти в моделях, которые это запрещают», Журнал алгоритмов , 4 (1): 45–50, doi : 10.1016/0196-6774(83)90033-0, MR  0689265.
22. Блеллох, Гай Э. (1990). Векторные модели для параллельных вычислений . Кембридж, Массачусетс: MIT Press. ISBN 026202313X. ОСЛК  21761743.
23. Лейзерсон, Чарльз Э .; Абухамде, Захи С.; Дуглас, Дэвид С.; Фейнман, Карл Р.; Ганмухи, Махеш Н.; Хилл, Джеффри В.; Хиллис, В. Дэниел ; Кушмаул, Брэдли С.; Сен-Пьер, Маргарет А. (15 марта 1996 г.). «Сетевая архитектура соединительной машины CM-5». Журнал параллельных и распределенных вычислений . 33 (2): 145–158. дои : 10.1006/jpdc.1996.0033. ISSN  0743-7315.
24. Уоррен, Генри С. (2003), Hacker's Delight, Аддисон-Уэсли, стр. 236, ISBN 978-0-201-91465-8.
25. Эгечиоглу, О.; Галлопулос, Э.; Коч, К. (1990), «Параллельный метод для быстрой и практичной интерполяции Ньютона высокого порядка», BIT Computer Science and Numerical Mathematics , 30 (2): 268–288, doi : 10.1007/BF02017348, S2CID  9607531.
26. Эгечиоглу, О.; Галлопулос, Э.; Коч, К. (1989), «Быстрое вычисление разделенных разностей и параллельная интерполяция Эрмита», Journal of Complexity , 5 (4): 417–437, doi : 10.1016/0885-064X(89)90018-6

Внешние ссылки

• Вайсштейн, Эрик В. «Накопленная сумма». Математический мир .