Спектральная кластеризация

Методы кластеризации

Пример связного графа с 6 вершинами.

Разбиение на два связанных графа

В многомерной статистике спектральные методы кластеризации используют спектр ( собственные значения ) матрицы сходства данных для выполнения снижения размерности перед кластеризацией в меньшем количестве измерений. Матрица сходства предоставляется в качестве входных данных и состоит из количественной оценки относительного сходства каждой пары точек в наборе данных.

Применительно к сегментации изображений спектральная кластеризация известна как категоризация объектов на основе сегментации .

Определения

При наличии перечисленного набора точек данных матрица подобия может быть определена как симметричная матрица , где представляет собой меру подобия между точками данных с индексами и . Общий подход к спектральной кластеризации заключается в использовании стандартного метода кластеризации (существует много таких методов, k -средние обсуждаются ниже) на соответствующих собственных векторах матрицы Лапласа . Существует много различных способов определения Лапласа, которые имеют различные математические интерпретации, и поэтому кластеризация также будет иметь различные интерпретации. Релевантными собственными векторами являются те, которые соответствуют нескольким наименьшим собственным значениям Лапласа, за исключением наименьшего собственного значения, которое будет иметь значение 0. Для эффективности вычислений эти собственные векторы часто вычисляются как собственные векторы, соответствующие наибольшим нескольким собственным значениям функции Лапласа. ${\displaystyle A}$ ${\displaystyle A_{ij}\geq 0}$ ${\displaystyle i}$ ${\displaystyle j}$ ${\displaystyle A}$

Матрица Лапласа

Двумерная пружинная система.

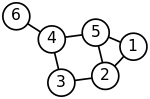
Спектральная кластеризация, как хорошо известно, связана с разбиением системы масса-пружина, где каждая масса связана с точкой данных, а каждая жесткость пружины соответствует весу ребра, описывающего сходство двух связанных точек данных, как в системе пружины . В частности, классическая ссылка ^{[1] объясняет, что задача на собственные значения, описывающая поперечные моды колебаний системы масса-пружина, в точности совпадает с задачей на собственные значения для} матрицы Лапласа графа, определяемой как

${\displaystyle L:=D-A}$,

где диагональная матрица ${\displaystyle D}$

${\displaystyle D_{ii}=\sum _{j}A_{ij},}$

и A — матрица смежности .

Массы, которые плотно связаны пружинами в системе масса-пружина, очевидно, движутся вместе из положения равновесия в низкочастотных модах колебаний, так что компоненты собственных векторов, соответствующие наименьшим собственным значениям графа Лапласа, могут быть использованы для осмысленной кластеризации масс. Например, предполагая, что все пружины и массы идентичны в изображенной двумерной системе пружин, можно было бы интуитивно ожидать, что наиболее слабо связанные массы в правой части системы будут двигаться с наибольшей амплитудой и в противоположном направлении относительно остальных масс, когда система встряхивается — и это ожидание будет подтверждено анализом компонентов собственных векторов графа Лапласа, соответствующих наименьшим собственным значениям, т. е. наименьшим частотам колебаний .

Нормализация матрицы Лапласа

Цель нормализации — сделать все диагональные элементы матрицы Лапласа единичными, а также соответствующим образом масштабировать недиагональные элементы. В взвешенном графе вершина может иметь большую степень из-за небольшого числа связанных ребер, но с большими весами, а также из-за большого числа связанных ребер с единичными весами.

Популярный метод нормализованной спектральной кластеризации — это алгоритм нормализованных разрезов или алгоритм Ши–Малика, представленный Цзяньбо Ши и Джитендрой Маликом [2] , ^[2] обычно используемый для сегментации изображений . Он разбивает точки на два набора на основе собственного вектора, соответствующего второму наименьшему собственному значению симметричного нормализованного лапласиана, определяемого как ${\displaystyle (B_{1},B_{2})}$ ${\displaystyle v}$

${\displaystyle L^{\text{norm}}:=I-D^{-1/2}AD^{-1/2}.}$

Вектор также является собственным вектором, соответствующим второму по величине собственному значению симметрично нормализованной матрицы смежности. ${\displaystyle v}$ ${\displaystyle D^{-1/2}AD^{-1/2}.}$

Случайный блуждающий (или левый) нормализованный Лапласиан определяется как

${\displaystyle L^{\text{rw}}:=D^{-1}L=I-D^{-1}A}$

и также может быть использован для спектральной кластеризации. Математически эквивалентный алгоритм ^[3] берет собственный вектор, соответствующий наибольшему собственному значению случайного блуждания нормализованной матрицы смежности . ${\displaystyle u}$ ${\displaystyle P=D^{-1}A}$

Собственный вектор симметрично нормализованного Лапласа и собственный вектор левонормализованного Лапласа связаны тождеством ${\displaystyle v}$ ${\displaystyle u}$ ${\displaystyle D^{-1/2}v=u.}$

Кластерный анализчерез спектральное вложение

Зная матрицу выбранных собственных векторов, выполняется отображение — называемое спектральным вложением — исходных точек данных в -мерное векторное пространство с использованием строк . Теперь анализ сводится к кластеризации векторов с компонентами, что может быть сделано различными способами. ${\displaystyle n}$ ${\displaystyle k}$ ${\displaystyle V}$ ${\displaystyle n}$ ${\displaystyle k}$ ${\displaystyle V}$ ${\displaystyle k}$

В простейшем случае выбранный одиночный собственный вектор , называемый вектором Фидлера , соответствует второму наименьшему собственному значению. Используя компоненты одного, можно поместить все точки, компонент которых в положителен, в набор , а остальные в , таким образом, разделив график на два и пометив точки данных двумя метками. Этот подход на основе знаков следует интуитивному объяснению спектральной кластеризации с помощью модели массы-пружины — в низкочастотном режиме вибрации, который представляет вектор Фидлера , точки данных одного кластера, идентифицированные с взаимно сильно связанными массами, будут двигаться вместе в одном направлении, в то время как в точках данных дополнительного кластера, идентифицированных с оставшимися массами, будут двигаться вместе в противоположном направлении. Алгоритм можно использовать для иерархической кластеризации путем многократного разделения подмножеств таким же образом. ${\displaystyle k=1}$ ${\displaystyle v}$ ${\displaystyle v,}$ ${\displaystyle v}$ ${\displaystyle B_{+}}$ ${\displaystyle B_{-}}$ ${\displaystyle v}$

В общем случае можно использовать любой метод векторной кластеризации, например, DBSCAN . ${\displaystyle k>1}$

Алгоритмы

Базовый алгоритм

1. Вычислить Лапласиан (или нормализованный Лапласиан) ${\displaystyle L}$
2. Вычислите первые собственные векторы (собственные векторы, соответствующие наименьшим собственным значениям ) ${\displaystyle k}$ ${\displaystyle k}$ ${\displaystyle L}$
3. Рассмотрим матрицу, образованную первыми собственными векторами; -я строка определяет характеристики узла графа ${\displaystyle k}$ ${\displaystyle l}$ ${\displaystyle l}$
4. Кластеризуйте узлы графа на основе этих признаков (например, с помощью кластеризации k-средних )

Если матрица подобия еще не была явно построена, эффективность спектральной кластеризации может быть улучшена, если решение соответствующей задачи на собственные значения выполняется безматричным способом (без явного манипулирования или даже вычисления матрицы подобия), как в алгоритме Ланцоша . ${\displaystyle A}$

Для графов большого размера второе собственное значение (нормализованной) матрицы Лапласа графа часто плохо обусловлено , что приводит к медленной сходимости итеративных решателей собственных значений. Предварительная подготовка является ключевой технологией, ускоряющей сходимость, например, в методе LOBPCG без матриц . Спектральная кластеризация успешно применялась к большим графам, сначала определяя их структуру сообщества , а затем кластеризуя сообщества. ^[4]

Спектральная кластеризация тесно связана с нелинейным уменьшением размерности , а методы уменьшения размерности, такие как локально-линейное встраивание, могут использоваться для уменьшения ошибок, вызванных шумом или выбросами. ^[5]

Расходы

Обозначая число точек данных как , важно оценить объем памяти и время вычислений или число выполненных арифметических операций (AO) как функцию . Независимо от алгоритма спектральной кластеризации, двумя основными затратными пунктами являются построение графа Лапласа и определение его собственных векторов для спектрального встраивания. Последний шаг — определение меток из матрицы собственных векторов — обычно является наименее затратным, требуя только AO и создания только вектора меток в памяти. ${\displaystyle n}$ ${\displaystyle n}$ ${\displaystyle k}$ ${\displaystyle n}$ ${\displaystyle k}$ ${\displaystyle kn}$ ${\displaystyle n}$ ${\displaystyle 1}$

Необходимость построения графового Лапласа является общей для всех методов кластеризации на основе расстояний или корреляций. Вычисление собственных векторов характерно только для спектральной кластеризации.

Построение графа Лапласа

Графовый лапласиан может быть и обычно строится из матрицы смежности. Построение может быть выполнено без матрицы, т. е. без явного формирования матрицы графового лапласиана и без АО. Его также можно выполнить вместо матрицы смежности без увеличения объема памяти. В любом случае, затраты на построение графового лапласиана по сути определяются затратами на построение матрицы смежности -по- графу. ${\displaystyle n}$ ${\displaystyle n}$

Более того, нормализованный Лапласиан имеет точно такие же собственные векторы, как и нормализованная матрица смежности, но с обратным порядком собственных значений. Таким образом, вместо вычисления собственных векторов, соответствующих наименьшим собственным значениям нормализованного Лапласа, можно эквивалентно вычислить собственные векторы, соответствующие наибольшим собственным значениям нормализованной матрицы смежности, даже не говоря о матрице Лапласа.

Наивные конструкции матрицы смежности графа , например, с использованием ядра RBF, делают ее плотной, требуя, таким образом, памяти и АО для определения каждого из элементов матрицы. Метод Нистрома ^[6] может быть использован для аппроксимации матрицы сходства, но аппроксимированная матрица не является поэлементно положительной, ^[7] т.е. не может быть интерпретирована как сходство на основе расстояния. ${\displaystyle n^{2}}$ ${\displaystyle n^{2}}$ ${\displaystyle n^{2}}$

Алгоритмы построения матрицы смежности графа как разреженной матрицы обычно основаны на поиске ближайшего соседа , который оценивает или выбирает окрестность заданной точки данных для ближайших соседей и вычисляет ненулевые элементы матрицы смежности, сравнивая только пары соседей. Таким образом, количество выбранных ближайших соседей определяет количество ненулевых элементов и часто фиксируется, так что объем памяти матрицы смежности графа составляет всего , для вычисления ненулевых элементов требуются только последовательные арифметические операции , и вычисления можно тривиально выполнять параллельно. ${\displaystyle n}$ ${\displaystyle n}$ ${\displaystyle O(n)}$ ${\displaystyle O(n)}$ ${\displaystyle O(n)}$

Вычисление собственных векторов

Стоимость вычисления матрицы -by- (с ) выбранных собственных векторов графового лапласиана обычно пропорциональна стоимости умножения матрицы -by- графового лапласиана на вектор, которая сильно варьируется в зависимости от того, плотная или разреженная матрица графового лапласиана. Для плотного случая стоимость, таким образом, составляет . Очень часто цитируемая в литературе стоимость исходит из выбора и явно вводит в заблуждение, поскольку, например, в иерархической спектральной кластеризации , определяемой вектором Фидлера . ${\displaystyle n}$ ${\displaystyle k}$ ${\displaystyle k\ll n}$ ${\displaystyle n}$ ${\displaystyle n}$ ${\displaystyle O(n^{2})}$ ${\displaystyle O(n^{3})}$ ${\displaystyle k=n}$ ${\displaystyle k=1}$

В разреженном случае матрицы Лапласа -by- graph с ненулевыми элементами стоимость произведения матрицы на вектор и, следовательно, вычисления матрицы -by- with выбранных собственных векторов составляет , с занимаемой памятью также только — оба являются оптимальными нижними границами сложности кластеризации точек данных. Более того, решатели собственных значений без матриц, такие как LOBPCG, могут эффективно работать параллельно, например, на нескольких графических процессорах с распределенной памятью, что приводит не только к высококачественным кластерам, которыми славится спектральная кластеризация, но и к наивысшей производительности. ^[8] ${\displaystyle n}$ ${\displaystyle n}$ ${\displaystyle O(n)}$ ${\displaystyle n}$ ${\displaystyle k}$ ${\displaystyle k\ll n}$ ${\displaystyle O(n)}$ ${\displaystyle O(n)}$ ${\displaystyle n}$

Программное обеспечение

Бесплатное программное обеспечение, реализующее спектральную кластеризацию, доступно в крупных проектах с открытым исходным кодом, таких как scikit-learn ^[9] с использованием LOBPCG ^[10] с многосеточным предварительным обусловливанием ^{[11] [12]} или ARPACK , MLlib для кластеризации псевдособственных векторов с использованием метода степенной итерации ^[13] и R ^[14] .

Связь с другими методами кластеризации

Идеи, лежащие в основе спектральной кластеризации, могут быть не очевидны. Может быть полезно выделить связи с другими методами. В частности, ее можно описать в контексте методов ядерной кластеризации, что выявляет несколько сходств с другими подходами. ^[15]

Отношения ск-означает

Задача взвешенного ядра k -средних ^[16] разделяет целевую функцию с задачей спектральной кластеризации, которую можно оптимизировать напрямую с помощью многоуровневых методов. ^[17]

Связь с DBSCAN

В тривиальном случае определения компонентов связного графа — оптимальных кластеров без разрезов ребер — спектральная кластеризация также связана со спектральной версией кластеризации DBSCAN , которая находит компоненты, связанные по плотности. ^[18]

Меры для сравнения кластеров

Рави Каннан, Сантош Вемпала и Адриан Ветта ^[19] предложили бикритериальную меру для определения качества заданной кластеризации. Они сказали, что кластеризация является (α, ε)-кластеризацией, если проводимость каждого кластера (в кластеризации) составляет не менее α, а вес межкластерных ребер составляет не более ε доли от общего веса всех ребер в графе. Они также рассматривают два алгоритма аппроксимации в той же статье.

История и смежная литература

Спектральная кластеризация имеет долгую историю. ^{[20] [21] [22] [23] [24] [2] [25]} Спектральная кластеризация как метод машинного обучения была популяризирована Ши и Маликом ^[2] и Нг, Джорданом и Вайсом. ^[25]

Идеи и сетевые меры, связанные со спектральной кластеризацией, также играют важную роль в ряде приложений, явно отличных от проблем кластеризации. Например, сети с более сильными спектральными разбиениями требуют больше времени для сходимости в моделях обновления мнений, используемых в социологии и экономике. ^{[26] [27]}

Смотрите также

• Распространение сродства
• Анализ главных компонент ядра
• Кластерный анализ
• Теория спектральных графов

Ссылки

1. Деммель, Дж. «CS267: Заметки к лекции 23, 9 апреля 1999 г., Разбиение графов, часть 2».
2. Цзяньбо Ши и Джитендра Малик, «Нормализованные разрезы и сегментация изображений», IEEE Transactions on PAMI, том 22, № 8, август 2000 г.
3. Марина Мейла и Цзяньбо Ши, «Сегментация обучения с помощью случайных блужданий», Neural Information Processing Systems 13 (NIPS 2000), 2001, стр. 873–879.
4. Заре, Хабил; Шуштари, П.; Гупта, А.; Бринкман, Р. (2010). «Сокращение данных для спектральной кластеризации для анализа данных высокопроизводительной проточной цитометрии». BMC Bioinformatics . 11 : 403. doi : 10.1186/1471-2105-11-403 . PMC 2923634. PMID  20667133 . 
5. Ариас-Кастро, Э.; Чен, Г.; Лерман, Г. (2011), «Спектральная кластеризация на основе локальных линейных приближений», Electronic Journal of Statistics , 5 : 1537–87, arXiv : 1001.1323 , doi : 10.1214/11-ejs651, S2CID  88518155
6. Fowlkes, C (2004). «Спектральная группировка с использованием метода Нистрома». IEEE Transactions on Pattern Analysis and Machine Intelligence . 26 (2): 214–25. doi :10.1109/TPAMI.2004.1262185. PMID  15376896. S2CID  2384316.
7. Ван, С.; Гиттенс, А.; Махони, М. В. (2019). «Масштабируемая кластеризация ядра K-средних с приближением Нистрома: границы относительной погрешности». Журнал исследований машинного обучения . 20 : 1–49. arXiv : 1706.02803 .
8. Асер, Сехер; Боман, Эрик Г.; Глуса, Кристиан А.; Раджаманикам, Сивасанкаран (2021 г.). «Sphynx: параллельный разделитель графов с несколькими графическими процессорами для систем с распределенной памятью». Параллельные вычисления . 106 : 102769. arXiv : 2105.00578 . doi : 10.1016/j.parco.2021.102769. S2CID  233481603.
9. "2.3. Кластеризация".
10. Князев, Эндрю В. (2003). Боли; Диллон; Гош; Коган (ред.). Современные предобусловленные собственные решатели для спектральной сегментации изображений и деления графа пополам. Кластеризация больших наборов данных; Третья международная конференция IEEE по интеллектуальному анализу данных (ICDM 2003) Мельбурн, Флорида: IEEE Computer Society. стр. 59–62.
11. Князев, Эндрю В. (2006). Многомасштабная спектральная сегментация изображений. Многомасштабная предварительная подготовка для вычисления собственных значений графовых лапласианов в сегментации изображений. Семинар по быстрому изучению многообразий, WM Williamburg, VA. doi :10.13140/RG.2.2.35280.02565.
12. Князев, Эндрю В. (2006). Многомасштабное спектральное разбиение графа и сегментация изображения. Практикум по алгоритмам для современных массивных наборов данных Стэнфордского университета и Yahoo! Research.
13. «Кластеризация — API на основе RDD — Документация Spark 3.2.0».
14. "Kernlab: Лаборатория машинного обучения на основе ядра". 12 ноября 2019 г.
15. Filippone, M.; Camastra, F.; Masulli, F.; Rovetta, S. (январь 2008 г.). «Обзор ядерных и спектральных методов кластеризации» (PDF) . Pattern Recognition . 41 (1): 176–190. Bibcode :2008PatRe..41..176F. doi :10.1016/j.patcog.2007.05.018.
16. Dhillon, IS; Guan, Y.; Kulis, B. (2004). "Kernel k-means: spectrumal clustering and normalized cuts" (PDF) . Труды десятой международной конференции ACM SIGKDD по обнаружению знаний и добыче данных . стр. 551–6.
17. Диллон, Индерджит; Гуань, Юйцян; Кулис, Брайан (ноябрь 2007 г.). «Взвешенные разрезы графа без собственных векторов: многоуровневый подход». Труды IEEE по анализу шаблонов и машинному интеллекту . 29 (11): 1944–1957. CiteSeerX 10.1.1.131.2635 . doi :10.1109/tpami.2007.1115. PMID  17848776. S2CID  9402790. 
18. Шуберт, Эрих; Гесс, Сибилла; Морик, Катарина (2018). Связь DBSCAN с матричной факторизацией и спектральной кластеризацией (PDF) . LWDA. стр. 330–334.
19. Каннан, Рави; Вемпала, Сантош; Ветта, Адриан (2004). «О кластеризации: хорошая, плохая и спектральная». Журнал ACM . 51 (3): 497–515. doi :10.1145/990308.990313. S2CID  207558562.
20. Чигер, Джефф (1969). «Нижняя граница для наименьшего собственного значения лапласиана». Труды Принстонской конференции в честь профессора С. Бохнера .
21. Донат, Уильям; Хоффман, Алан (1972). «Алгоритмы разбиения графов и компьютерная логика на основе собственных векторов матриц связей». Технический бюллетень раскрытия информации IBM .
22. Фидлер, Мирослав (1973). «Алгебраическая связность графов». Czechoslovak Mathematical Journal . 23 (2): 298–305. doi : 10.21136/CMJ.1973.101168 .
23. Гваттери, Стивен; Миллер, Гэри Л. (1995). «О производительности методов разбиения спектральных графов». Ежегодный симпозиум ACM-SIAM по дискретным алгоритмам .
24. Дэниел А. Шпильман и Шан-Хуа Тэн (1996). «Работы по спектральному разбиению: планарные графы и сетки конечных элементов». Ежегодный симпозиум IEEE по основам компьютерной науки .
25. Ng, Andrew Y.; Jordan, Michael I.; Weiss, Yair (2002). "О спектральной кластеризации: анализ и алгоритм" (PDF) . Достижения в области нейронных систем обработки информации .
26. ДеМарзо, П. М.; Ваянос, Д.; Цвибель, Дж. (2003-08-01). «Предвзятость убеждения, социальное влияние и одномерные мнения». Ежеквартальный журнал экономики . 118 (3). Oxford University Press: 909–968. doi : 10.1162/00335530360698469. ISSN  0033-5533.
27. Голуб, Бенджамин; Джексон, Мэтью О. (2012-07-26). «Как гомофилия влияет на скорость обучения и динамику наилучшего ответа». The Quarterly Journal of Economics . 127 (3). Oxford University Press (OUP): 1287–1338. doi :10.1093/qje/qjs021. ISSN  0033-5533.