алгоритм Штрассена

Рекурсивный алгоритм умножения матриц

В линейной алгебре алгоритм Штрассена , названный в честь Фолькера Штрассена , — это алгоритм умножения матриц . Он быстрее стандартного алгоритма умножения матриц для больших матриц, с лучшей асимптотической сложностью , хотя наивный алгоритм часто лучше для меньших матриц. Алгоритм Штрассена медленнее самых быстрых известных алгоритмов для чрезвычайно больших матриц, но такие галактические алгоритмы бесполезны на практике, так как они намного медленнее для матриц практичного размера. Для маленьких матриц существуют даже более быстрые алгоритмы.

Алгоритм Штрассена работает для любого кольца , например, плюс/умножение, но не для всех полуколец , например, мин-плюс или булева алгебра , где наивный алгоритм все еще работает, и для так называемого комбинаторного умножения матриц.

История

Фолькер Штрассен впервые опубликовал этот алгоритм в 1969 году и тем самым доказал, что общий алгоритм умножения матриц не является оптимальным. ^[1] Публикация алгоритма Штрассена привела к большему количеству исследований умножения матриц, что привело как к асимптотическим нижним границам, так и к улучшенным вычислительным верхним границам. ${\displaystyle n^{3}}$

Алгоритм

Левый столбец визуализирует вычисления, необходимые для определения результата умножения матриц 2x2 . Наивное умножение матриц требует одного умножения для каждой «1» левого столбца. Каждый из других столбцов (M1-M7) представляет одно из 7 умножений в алгоритме Штрассена. Сумма столбцов M1-M7 дает тот же результат, что и полное умножение матриц слева.

Пусть , будут двумя квадратными матрицами над кольцом , например, матрицы, элементы которых являются целыми числами или действительными числами. Целью умножения матриц является вычисление матричного произведения . Следующее изложение алгоритма предполагает, что все эти матрицы имеют размеры, являющиеся степенями двойки (т. е. ), но это необходимо только концептуально — если матрицы , не имеют типа , «отсутствующие» строки и столбцы можно заполнить нулями, чтобы получить матрицы с размерами степеней двойки — хотя реальные реализации алгоритма на практике этого не делают. ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle {\mathcal {R}}}$ ${\displaystyle C=AB}$ ${\displaystyle A,\,B,\,C\in \operatorname {Matr} _{2^{n}\times 2^{n}}({\mathcal {R}})}$ ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle 2^{n}\times 2^{n}}$

Алгоритм Штрассена разбивает и на блочные матрицы одинакового размера ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle C}$

${\displaystyle A={\begin{bmatrix}A_{11}&A_{12}\\A_{21}&A_{22}\end{bmatrix}},\quad B={\begin{bmatrix}B_{11}&B_{12}\\B_{21}&B_{22}\end{bmatrix}},\quad C={\begin{bmatrix}C_{11}&C_{12}\\C_{21}&C_{22}\end{bmatrix}},\quad }$

с . Наивный алгоритм будет таким: ${\displaystyle A_{ij},B_{ij},C_{ij}\in \operatorname {Mat} _{2^{n-1}\times 2^{n-1}}({\mathcal {R}})}$

${\displaystyle {\begin{bmatrix}C_{11}&C_{12}\\C_{21}&C_{22}\end{bmatrix}}={\begin{bmatrix}A_{11}{\color {red}\times }B_{11}+A_{12}{\color {red}\times }B_{21}\quad &A_{11}{\color {red}\times }B_{12}+A_{12}{\color {red}\times }B_{22}\\A_{21}{\color {red}\times }B_{11}+A_{22}{\color {red}\times }B_{21}\quad &A_{21}{\color {red}\times }B_{12}+A_{22}{\color {red}\times }B_{22}\end{bmatrix}}.}$

Эта конструкция не уменьшает количество умножений: для вычисления матриц по-прежнему необходимо 8 умножений матричных блоков, столько же умножений требуется при использовании стандартного умножения матриц. ${\displaystyle C_{ij}}$

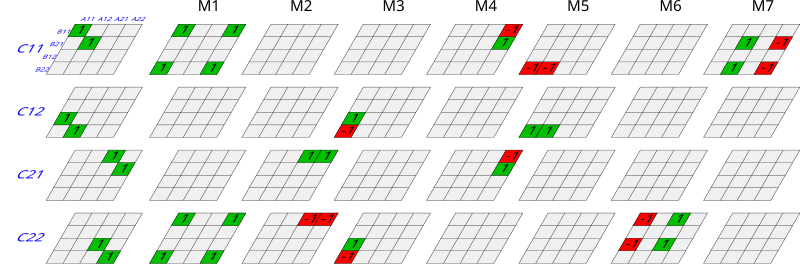
Алгоритм Штрассена вместо этого определяет новые значения:

${\displaystyle {\begin{aligned}M_{1}&=(A_{11}+A_{22}){\color {red}\times }(B_{11}+B_{22});\\M_{2}&=(A_{21}+A_{22}){\color {red}\times }B_{11};\\M_{3}&=A_{11}{\color {red}\times }(B_{12}-B_{22});\\M_{4}&=A_{22}{\color {red}\times }(B_{21}-B_{11});\\M_{5}&=(A_{11}+A_{12}){\color {red}\times }B_{22};\\M_{6}&=(A_{21}-A_{11}){\color {red}\times }(B_{11}+B_{12});\\M_{7}&=(A_{12}-A_{22}){\color {red}\times }(B_{21}+B_{22}),\\\end{aligned}}}$

используя только 7 умножений (по одному для каждого ) вместо 8. Теперь мы можем выразить через : ${\displaystyle M_{k}}$ ${\displaystyle C_{ij}}$ ${\displaystyle M_{k}}$

${\displaystyle {\begin{bmatrix}C_{11}&C_{12}\\C_{21}&C_{22}\end{bmatrix}}={\begin{bmatrix}M_{1}+M_{4}-M_{5}+M_{7}\quad &M_{3}+M_{5}\\M_{2}+M_{4}\quad &M_{1}-M_{2}+M_{3}+M_{6}\end{bmatrix}}.}$

Мы рекурсивно повторяем этот процесс деления до тех пор, пока подматрицы не выродятся в числа (элементы кольца ). Если, как упоминалось выше, исходная матрица имела размер, который не был степенью 2, то полученное произведение будет иметь нулевые строки и столбцы, как и , и они затем будут удалены в этой точке, чтобы получить (меньшую) матрицу, которую мы действительно хотели. ${\displaystyle {\mathcal {R}}}$ ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle C}$

Практические реализации алгоритма Штрассена переключаются на стандартные методы умножения матриц для достаточно малых подматриц, для которых эти алгоритмы более эффективны. Конкретная точка пересечения, для которой алгоритм Штрассена более эффективен, зависит от конкретной реализации и оборудования. Более ранние авторы подсчитали, что алгоритм Штрассена быстрее для матриц шириной от 32 до 128 для оптимизированных реализаций. ^[2] Однако было замечено, что эта точка пересечения увеличивается в последние годы, и исследование 2010 года показало, что даже один шаг алгоритма Штрассена часто не приносит пользы на текущих архитектурах по сравнению с высокооптимизированным традиционным умножением, пока размеры матриц не превысят 1000 или более, и даже для размеров матриц в несколько тысяч преимущество обычно в лучшем случае незначительно (около 10% или меньше). ^[3] Более недавнее исследование (2016 г.) наблюдало преимущества для матриц размером от 512 и преимущество около 20%. ^[4]

форма Винограда

Можно сократить количество матричных сложений, используя вместо этого следующую форму, открытую Виноградом:

${\displaystyle {\begin{bmatrix}a&b\\c&d\end{bmatrix}}{\begin{bmatrix}A&C\\B&D\end{bmatrix}}={\begin{bmatrix}t+b{\color {red}\times }B&w+v+(a+b-c-d){\color {red}\times }D\\w+u+d{\color {red}\times }(B+C-A-D)&w+u+v\end{bmatrix}}}$

где . ${\displaystyle t=a{\color {red}\times }A,\;u=(c-a){\color {red}\times }(C-D),\;v=(c+d){\color {red}\times }(C-A),\;w=t+(c+d-a){\color {red}\times }(A+D-C)}$

Это сокращает количество сложений и вычитаний матриц с 18 до 15. Количество умножений матриц по-прежнему равно 7, а асимптотическая сложность та же. ^[5]

Асимптотическая сложность

Схема алгоритма выше показала, что можно обойтись всего 7, вместо традиционных 8, умножений матриц на матрицу для подблоков матрицы. С другой стороны, нужно делать сложения и вычитания блоков, хотя это не имеет значения для общей сложности: сложение матриц размера требует только операций, тогда как умножение существенно дороже (традиционно операции сложения или умножения). ${\displaystyle N/2}$ ${\displaystyle (N/2)^{2}}$ ${\displaystyle 2(N/2)^{3}}$

Тогда возникает вопрос, сколько именно операций требуется для алгоритмов Штрассена и как это соотносится со стандартным умножением матриц, которое требует приблизительно (где ) арифметических операций, т.е. имеет асимптотическую сложность . ${\displaystyle 2N^{3}}$ ${\displaystyle N=2^{n}}$ ${\displaystyle \Theta (N^{3})}$

Число сложений и умножений, требуемых в алгоритме Штрассена, можно вычислить следующим образом: пусть будет числом операций для матрицы. Затем, рекурсивно применяя алгоритм Штрассена, мы видим, что , для некоторой константы , которая зависит от числа сложений, выполняемых при каждом применении алгоритма. Следовательно , , т. е. асимптотическая сложность умножения матриц размера с использованием алгоритма Штрассена равна . Однако уменьшение числа арифметических операций достигается ценой несколько сниженной численной устойчивости , ^[6] и алгоритм также требует значительно больше памяти по сравнению с наивным алгоритмом. Обе исходные матрицы должны иметь расширенные размеры до следующей степени 2, что приводит к хранению в четыре раза большего количества элементов, а семь вспомогательных матриц содержат каждая четверть элементов в расширенных. ${\displaystyle f(n)}$ ${\displaystyle 2^{n}\times 2^{n}}$ ${\displaystyle f(n)=7f(n-1)+l4^{n}}$ ${\displaystyle l}$ ${\displaystyle f(n)=(7+o(1))^{n}}$ ${\displaystyle N=2^{n}}$ ${\displaystyle O([7+o(1)]^{n})=O(N^{\log _{2}7+o(1)})\approx O(N^{2.8074})}$

Алгоритм Штрассена необходимо сравнить с «наивным» способом выполнения умножения матриц, который потребовал бы 8 вместо 7 умножений подблоков. Это затем привело бы к сложности, которую можно ожидать от стандартного подхода: . Сравнение этих двух алгоритмов показывает, что асимптотически алгоритм Штрассена быстрее: существует размер , так что матрицы большего размера более эффективно умножаются алгоритмом Штрассена, чем «традиционным» способом. Однако асимптотическое утверждение не подразумевает, что алгоритм Штрассена всегда быстрее даже для небольших матриц, и на практике это фактически не так: для небольших матриц стоимость дополнительных добавлений блоков матриц перевешивает экономию в количестве умножений. Есть также другие факторы, не охваченные вышеприведенным анализом, такие как разница в стоимости сегодняшнего оборудования между загрузкой данных из памяти на процессоры и стоимостью фактического выполнения операций с этими данными. Вследствие таких соображений алгоритм Штрассена обычно используется только на «больших» матрицах. Этот эффект еще более выражен в альтернативных алгоритмах, таких как алгоритм Копперсмита и Винограда : хотя асимптотически он даже быстрее, точка кроссинговера настолько велика, что алгоритм обычно не используется на матрицах, с которыми приходится сталкиваться на практике. ${\displaystyle O(8^{n})=O(N^{\log _{2}8})=O(N^{3})}$ ${\displaystyle N_{\text{threshold}}}$ ${\displaystyle N_{\text{threshold}}}$

Ранговая или билинейная сложность

Билинейная сложность или ранг билинейного отображения является важным понятием в асимптотической сложности умножения матриц. Ранг билинейного отображения над полем F определяется как (несколько злоупотребление обозначениями ) ${\displaystyle \phi :\mathbf {A} \times \mathbf {B} \rightarrow \mathbf {C} }$

${\displaystyle R(\phi /\mathbf {F} )=\min \left\{r\left|\exists f_{i}\in \mathbf {A} ^{*},g_{i}\in \mathbf {B} ^{*},w_{i}\in \mathbf {C} ,\forall \mathbf {a} \in \mathbf {A} ,\mathbf {b} \in \mathbf {B} ,\phi (\mathbf {a} ,\mathbf {b} )=\sum _{i=1}^{r}f_{i}(\mathbf {a} )g_{i}(\mathbf {b} )w_{i}\right.\right\}}$

Другими словами, ранг билинейного отображения — это длина его кратчайшего билинейного вычисления. ^[7] Существование алгоритма Штрассена показывает, что ранг умножения матриц не больше семи. Чтобы увидеть это, выразим этот алгоритм (наряду со стандартным алгоритмом) как такое билинейное вычисление. В случае матриц двойственные пространства A * и B * состоят из отображений в поле F , индуцированных скалярным произведением с двумя точками (т.е. в этом случае суммой всех элементов произведения Адамара .) ${\displaystyle 2\times 2}$

Можно показать, что общее число элементарных умножений, требуемых для умножения матриц, асимптотически тесно связано с рангом , т. е . , или, более конкретно, поскольку константы известны, . Одним из полезных свойств ранга является то, что он является субмультипликативным для тензорных произведений , и это позволяет показать, что умножение матриц может быть выполнено не более чем за элементарные умножения для любого . (Это -кратное тензорное произведение отображения умножения матриц на себя — -я степень тензора — реализуется рекурсивным шагом в показанном алгоритме.) ${\displaystyle L}$ ${\displaystyle R}$ ${\displaystyle L=\Theta (R)}$ ${\displaystyle R/2\leq L\leq R}$ ${\displaystyle 2^{n}\times 2^{n}\times 2^{n}}$ ${\displaystyle 7n}$ ${\displaystyle n}$ ${\displaystyle n}$ ${\displaystyle 2\times 2\times 2}$ ${\displaystyle n}$

Поведение кэша

Алгоритм Штрассена не обращает внимания на кэш . Анализ его алгоритма поведения кэша показал, что он подвергается

${\displaystyle \Theta \left(1+{\frac {n^{2}}{b}}+{\frac {n^{\log _{2}7}}{b{\sqrt {M}}}}\right)}$

промахи кэша во время его выполнения, предполагая идеализированный кэш размером (т.е. со строками длиной ). ^{[8] : 13} ${\displaystyle M}$ ${\displaystyle M/b}$ ${\displaystyle b}$

Соображения по реализации

В описании выше указано, что матрицы являются квадратными, а их размер равен степени двойки, и что при необходимости следует использовать заполнение. Это ограничение позволяет рекурсивно делить матрицы пополам до тех пор, пока не будет достигнут предел скалярного умножения. Ограничение упрощает объяснение и анализ сложности, но на самом деле не является необходимым; ^[9] и на самом деле заполнение матрицы, как описано, увеличит время вычислений и может легко устранить довольно узкую экономию времени, полученную при использовании метода в первую очередь.

Хорошая реализация будет соответствовать следующим требованиям:

• Не обязательно или нежелательно использовать алгоритм Штрассена вплоть до предела скаляров. По сравнению с обычным умножением матриц, алгоритм добавляет значительную рабочую нагрузку в сложении/вычитании; поэтому ниже определенного размера лучше использовать обычное умножение. Таким образом, например, a не нужно дополнять до , поскольку его можно подразделить до матриц, и обычное умножение затем можно использовать на этом уровне. ${\displaystyle O(n^{2})}$ ${\displaystyle 1600\times 1600}$ ${\displaystyle 2048\times 2048}$ ${\displaystyle 25\times 25}$
• Метод действительно может быть применен к квадратным матрицам любого размера. ^[3] Если размер четный, они делятся пополам, как описано. Если размер нечетный, сначала применяется нулевое дополнение одной строкой и одним столбцом. Такое дополнение может применяться на лету и лениво, а дополнительные строки и столбцы отбрасываться по мере формирования результата. Например, предположим, что матрицы . Их можно разделить так, чтобы верхняя левая часть была , а нижняя правая — . Везде, где это требуется для операций, измерения дополняются нулями до первого. Обратите внимание, например, что произведение используется только в нижней строке вывода, поэтому требуется только иметь высоту строк; и, таким образом, левый множитель, используемый для его генерации, должен иметь высоту строк; соответственно, нет необходимости дополнять эту сумму до строк; необходимо только дополнять до столбцов, чтобы соответствовать . ${\displaystyle 199\times 199}$ ${\displaystyle 100\times 100}$ ${\displaystyle 99\times 99}$ ${\displaystyle 99}$ ${\displaystyle 100}$ ${\displaystyle M_{2}}$ ${\displaystyle 99}$ ${\displaystyle A_{21}+A_{22}}$ ${\displaystyle 99}$ ${\displaystyle 100}$ ${\displaystyle A_{22}}$ ${\displaystyle 100}$ ${\displaystyle A_{21}}$

Более того, нет необходимости, чтобы матрицы были квадратными. Неквадратные матрицы можно разделить пополам, используя те же методы, что даст меньшие неквадратные матрицы. Если матрицы достаточно неквадратные, то будет целесообразно сократить начальную операцию до более квадратных произведений, используя простые методы, которые по сути являются , например: ${\displaystyle O(n^{2})}$

• Произведение размера может быть выполнено в виде 20 отдельных операций, организованных для формирования результата; ${\displaystyle [2N\times N]\ast [N\times 10N]}$ ${\displaystyle [N\times N]\ast [N\times N]}$
• Произведение размера можно выполнить с помощью 10 отдельных операций, суммируя которые, получим результат. ${\displaystyle [N\times 10N]\ast [10N\times N]}$ ${\displaystyle [N\times N]\ast [N\times N]}$

Эти методы усложнят реализацию по сравнению с простым дополнением до квадрата степени двойки; однако разумно предположить, что любой, кто возьмется за реализацию метода Штрассена, а не обычного умножения, будет отдавать больший приоритет вычислительной эффективности, чем простоте реализации.

На практике алгоритм Штрассена может быть реализован для достижения лучшей производительности, чем обычное умножение, даже для матриц размером до , для матриц, которые совсем не являются квадратными, и без необходимости использования рабочего пространства за пределами буферов, которые уже необходимы для высокопроизводительного обычного умножения. ^[4] ${\displaystyle 500\times 500}$

Смотрите также

• Вычислительная сложность математических операций
• исключение Гаусса-Жордана
• Вычислительная сложность умножения матриц
• Кривая Z-порядка
• Алгоритм Карацубы для умножения n- значных целых чисел на время, а не на время ${\displaystyle O(n^{\log _{2}3})}$ ${\displaystyle O(n^{2})}$
  • Похожий алгоритм комплексного умножения умножает два комплексных числа, используя 3 действительных умножения вместо 4.
• Алгоритм Тума-Кука , более быстрое обобщение алгоритма Карацубы, которое позволяет проводить рекурсивную декомпозицию по принципу «разделяй и властвуй» на более чем 2 блока за раз.

Ссылки

1. Штрассен, Фолькер (1969). «Gaussian Elimination is not Optimal». Numer. Math . 13 (4): 354–356. doi :10.1007/BF02165411. S2CID  121656251.
2. Скиена, Стивен С. (1998), "§8.2.3 Матричное умножение", Руководство по разработке алгоритмов , Берлин, Нью-Йорк: Springer-Verlag , ISBN 978-0-387-94860-7.
3. D'Alberto, Paolo; Nicolau, Alexandru (2005). Использование рекурсии для повышения производительности ATLAS (PDF) . Шестой международный симпозиум по высокопроизводительным вычислениям.
4. Huang, Jianyu; Smith, Tyler M.; Henry, Greg M.; van de Geijn, Robert A. (13 ноября 2016 г.). Перезагрузка алгоритма Штрассена. SC16: Международная конференция по высокопроизводительным вычислениям, сетевым технологиям, хранению и анализу. IEEE Press. стр. 690–701. doi :10.1109/SC.2016.58. ISBN 9781467388153. Получено 1 ноября 2022 г. .
5. Кнут (1997), стр. 500.
6. Вебб, Миллер (1975). «Вычислительная сложность и численная устойчивость». SIAM J. Comput . 4 (2): 97–107. doi :10.1137/0204009.
7. Бургиссер; Клаузен; Шокроллахи (1997). Алгебраическая теория сложности . Спрингер-Верлаг. ISBN 3-540-60582-7.
8. Фриго, М.; Лейзерсон, К. Э.; Прокоп , Х.; Рамачандран, С. (1999). Алгоритмы, забывающие о кэше (PDF) . Труды симпозиума IEEE по основам компьютерной науки (FOCS). стр. 285–297.
9. Хайэм, Николас Дж. (1990). «Использование быстрого умножения матриц в BLAS уровня 3» (PDF) . ACM Transactions on Mathematical Software . 16 (4): 352–368. doi :10.1145/98267.98290. hdl : 1813/6900 . S2CID  5715053.

• Thomas H. Cormen , Charles E. Leiserson , Ronald L. Rivest и Clifford Stein . Introduction to Algorithms , Second Edition. MIT Press and McGraw-Hill, 2001. ISBN 0-262-03293-7 . Глава 28: Раздел 28.2: Алгоритм Штрассена для умножения матриц, стр. 735–741. 
• Кнут, Дональд (1997). Искусство программирования, получисленные алгоритмы . Том II (3-е изд.). Эддисон-Уэсли. ISBN 0-201-89684-2.

Внешние ссылки

• Вайсштейн, Эрик В. «Формулы Штрассена». Математический мир .(также включает формулы для быстрого обращения матрицы )
• Тайлер Дж. Эрнест, Алгоритм Штрассена на ячейке широкополосной связи