Аберрация (астрономия)

Явление, при котором объекты кажутся движущимися относительно своего истинного положения на небе.

Диаграмма, показывающая, как видимое положение звезды, наблюдаемое с Земли, может меняться в зависимости от скорости Земли. Эффект обычно намного меньше, чем показано.

В астрономии аберрация (также называемая астрономической аберрацией , звездной аберрацией или аберрацией скорости ) — это явление, при котором небесные объекты демонстрируют видимое движение относительно своего истинного положения в зависимости от скорости наблюдателя: Это заставляет объекты казаться смещенными по направлению движения наблюдателя. Изменение угла имеет порядок , где — скорость света , а — скорость наблюдателя . В случае «звездной» или «годовой» аберрации видимое положение звезды для наблюдателя на Земле периодически меняется в течение года, поскольку скорость Земли изменяется по мере ее вращения вокруг Солнца, на максимальный угол приблизительно 20  угловых секунд по прямому восхождению или склонению . ${\displaystyle v/c}$ ${\displaystyle c}$ ${\displaystyle v}$

Термин аберрация исторически использовался для обозначения ряда связанных явлений, касающихся распространения света в движущихся телах. ^[1] Аберрация отличается от параллакса , который представляет собой изменение видимого положения относительно близкого объекта, измеренного движущимся наблюдателем, относительно более удаленных объектов, которые определяют систему отсчета. Величина параллакса зависит от расстояния объекта от наблюдателя, тогда как аберрация — нет. Аберрация также связана с коррекцией светового времени и релятивистским излучением , хотя ее часто рассматривают отдельно от этих эффектов.

Аберрация имеет историческое значение из-за ее роли в развитии теорий света , электромагнетизма и, в конечном счете, теории специальной теории относительности . Впервые она была обнаружена в конце 1600-х годов астрономами, искавшими звездный параллакс для подтверждения гелиоцентрической модели Солнечной системы. Однако в то время ее не понимали как другое явление. ^[2] В 1727 году Джеймс Брэдли дал ей классическое объяснение в терминах конечной скорости света относительно движения Земли по орбите вокруг Солнца, ^{[3] [4],} которое он использовал для проведения одного из самых ранних измерений скорости света. Однако теория Брэдли была несовместима с теориями света 19-го века, и аберрация стала основной мотивацией для теорий увлечения эфиром Огюстена Френеля (в 1818 году) и Дж. Г. Стокса (в 1845 году), а также для эфирной теории электромагнетизма Хендрика Лоренца в 1892 году. Аберрация света, вместе с разработкой Лоренцом электродинамики Максвелла , проблемой движущегося магнита и проводника , экспериментами по отрицательному эфирному дрейфу , а также экспериментом Физо , привели Альберта Эйнштейна к разработке специальной теории относительности в 1905 году, которая представляет общую форму уравнения для аберрации в терминах такой теории. ^[5]

Объяснение

Световые лучи, падающие на Землю в системе покоя Солнца, в сравнении с теми же лучами в системе покоя Земли согласно специальной теории относительности. Эффект преувеличен для наглядности.

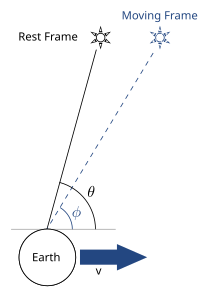
Аберрацию можно объяснить как разницу в угле падения луча света в различных инерциальных системах отсчета . Распространенной аналогией является рассмотрение кажущегося направления падающего дождя. Если дождь падает вертикально в системе отсчета человека, стоящего на месте, то для человека, движущегося вперед, дождь будет казаться идущим под углом, требуя от движущегося наблюдателя наклонить свой зонтик вперед. Чем быстрее движется наблюдатель, тем больший наклон необходим.

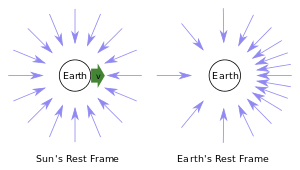
Чистый эффект заключается в том, что световые лучи, падающие на движущегося наблюдателя с боков в неподвижной системе отсчета, будут приходить под углом спереди в системе отсчета движущегося наблюдателя. Этот эффект иногда называют эффектом «прожектора» или «фары».

В случае годовой аберрации звездного света направление входящего звездного света, наблюдаемое в движущейся системе отсчета Земли, наклонено относительно угла, наблюдаемого в системе отсчета Солнца. Поскольку направление движения Земли меняется в течение ее орбиты, направление этого наклона меняется в течение года и приводит к тому, что видимое положение звезды отличается от ее истинного положения, измеренного в инерциальной системе отсчета Солнца.

Хотя классическое рассуждение дает интуицию для аберрации, оно приводит к ряду физических парадоксов, наблюдаемых даже на классическом уровне (см. историю). Для правильного учета аберрации требуется специальная теория относительности . Однако релятивистское объяснение очень похоже на классическое, и в обеих теориях аберрация может пониматься как случай сложения скоростей .

Классическое объяснение

В системе отсчета Солнца рассмотрим луч света со скоростью, равной скорости света , с компонентами скорости x и y и , и, таким образом, под углом таким, что . Если Земля движется со скоростью в направлении x относительно Солнца, то по сложению скоростей компонент x скорости луча в системе отсчета Земли равен , а скорость y неизменна, . Таким образом, угол света в системе отсчета Земли относительно угла в системе отсчета Солнца равен ${\displaystyle c}$ ${\displaystyle u_{x}}$ ${\displaystyle u_{y}}$ ${\displaystyle \theta }$ ${\displaystyle \tan(\theta )=u_{y}/u_{x}}$ ${\displaystyle v}$ ${\displaystyle u_{x}'=u_{x}+v}$ ${\displaystyle u_{y}'=u_{y}}$

${\displaystyle \tan(\phi )={\frac {u_{y}'}{u_{x}'}}={\frac {u_{y}}{u_{x}+v}}={\frac {\sin(\theta )}{v/c+\cos(\theta )}}}$

В случае этот результат сводится к , что в пределе может быть аппроксимировано значением . ${\displaystyle \theta =90^{\circ }}$ ${\displaystyle \tan(\theta -\phi )=v/c}$ ${\displaystyle v/c\ll 1}$ ${\displaystyle \theta -\phi =v/c}$

Релятивистское объяснение

Рассуждения в релятивистском случае те же самые, за исключением того, что должны использоваться релятивистские формулы сложения скоростей , которые могут быть выведены из преобразований Лоренца между различными системами отсчета. Эти формулы имеют вид

${\displaystyle u_{x}'=(u_{x}+v)/(1+u_{x}v/c^{2})}$

${\displaystyle u_{y}'=u_{y}/\gamma (1+u_{x}v/c^{2})}$

где , давая компоненты светового луча в системе отсчета Земли через компоненты в системе отсчета Солнца. Угол луча в системе отсчета Земли, таким образом, ^[6] ${\displaystyle \gamma =1/{\sqrt {1-v^{2}/c^{2}}}}$

${\displaystyle \tan(\phi )={\frac {u_{y}'}{u_{x}'}}={\frac {u_{y}}{\gamma (u_{x}+v)}}={\frac {\sin(\theta )}{\gamma (v/c+\cos(\theta ))}}}$

В случае этот результат сводится к , и в пределе это может быть аппроксимировано . Этот релятивистский вывод сохраняет скорость света постоянной во всех системах отсчета, в отличие от классического вывода, приведенного выше. ${\displaystyle \theta =90^{\circ }}$ ${\displaystyle \sin(\theta -\phi )=v/c}$ ${\displaystyle v/c\ll 1}$ ${\displaystyle \theta -\phi =v/c}$ ${\displaystyle {\sqrt {u_{x}^{2}+u_{y}^{2}}}=c}$

Связь с коррекцией светового времени и релятивистским излучением

Аберрацию, коррекцию светового времени и релятивистское излучение можно считать одним и тем же явлением в зависимости от системы отсчета.

Аберрация связана с двумя другими явлениями: коррекцией светового времени , которая возникает из-за движения наблюдаемого объекта в течение времени, необходимого его свету, чтобы достичь наблюдателя, и релятивистским излучением , которое представляет собой наклон света, испускаемого движущимся источником света. Его можно считать эквивалентным им, но в другой инерциальной системе отсчета. При аберрации наблюдатель считается движущимся относительно (для простоты ^[7] ) неподвижного источника света, в то время как при коррекции светового времени и релятивистском излучении источник света считается движущимся относительно неподвижного наблюдателя.

Рассмотрим случай наблюдателя и источника света, движущихся относительно друг друга с постоянной скоростью, при этом луч света движется от источника к наблюдателю. В момент излучения луч в системе покоя наблюдателя наклонен по сравнению с лучом в системе покоя источника, как это понимается через релятивистское излучение. За то время, которое требуется лучу света, чтобы достичь наблюдателя, источник света перемещается в системе наблюдателя, и «истинное положение» источника света смещается относительно видимого положения, которое видит наблюдатель, как объясняется коррекцией светового времени. Наконец, луч в системе наблюдателя в момент наблюдения наклонен по сравнению с лучом в системе источника, что можно понимать как аберрационный эффект. Таким образом, человек в системе источника света будет описывать видимый наклон луча в терминах аберрации, в то время как человек в системе наблюдателя будет описывать его как эффект светового времени.

Связь между этими явлениями действительна только в том случае, если системы отсчета наблюдателя и источника являются инерциальными. На практике, поскольку Земля не является инерциальной системой отсчета, а испытывает центростремительное ускорение по направлению к Солнцу, многие аберрационные эффекты, такие как годовая аберрация на Земле, не могут считаться поправками за световое время. Однако, если время между испусканием и обнаружением света коротко по сравнению с орбитальным периодом Земли, Землю можно аппроксимировать как инерциальную систему отсчета, а аберрационные эффекты эквивалентны поправкам за световое время.

Типы

В Астрономическом альманахе описывается несколько различных типов аберраций, возникающих из-за различных компонентов движения Земли и наблюдаемых объектов:

• Звездная аберрация: «Кажущееся угловое смещение наблюдаемого положения небесного тела, возникающее в результате движения наблюдателя. Звездная аберрация делится на суточную, годовую и вековую составляющие».
  • Годовая аберрация: «Компонента звездной аберрации, возникающая в результате движения Земли вокруг Солнца».
  • Суточная аберрация: «Компонента звездной аберрации, возникающая в результате суточного движения наблюдателя вокруг центра Земли из-за вращения Земли».
  • Вековая аберрация: «Компонента звездной аберрации, возникающая в результате практически равномерного и почти прямолинейного движения всей Солнечной системы в пространстве. Вековая аберрация обычно не принимается во внимание».
• Планетарная аберрация: «Кажущееся угловое смещение наблюдаемого положения тела солнечной системы от его мгновенного геоцентрического направления, как это было бы видно наблюдателю в геоцентре. Это смещение вызвано аберрацией света и смещением света во времени ». ^[8]

Ежегодное отклонение

Звезды на полюсах эклиптики кажутся движущимися по окружностям, звезды точно в плоскости эклиптики движутся по линиям, а звезды под промежуточными углами движутся по эллипсам. Здесь показаны видимые движения звезд с эклиптической широтой, соответствующей этим случаям, и с эклиптической долготой 270°.

Направление аберрации звезды на северном полюсе эклиптики различается в разное время года.

Годовая аберрация вызвана движением наблюдателя на Земле , когда планета вращается вокруг Солнца . Из-за орбитального эксцентриситета орбитальная скорость Земли (в системе покоя Солнца) периодически меняется в течение года, когда планета пересекает свою эллиптическую орбиту , и, следовательно, аберрация также периодически меняется, обычно заставляя звезды казаться движущимися по небольшим эллипсам . ${\displaystyle v}$

Приближая орбиту Земли к круговой, максимальное смещение звезды из-за годовой аберрации известно как постоянная аберрации , условно представленная как . Его можно рассчитать с помощью соотношения, подставляя среднюю скорость Земли в системе отсчета Солнца вместо и скорость света . Его принятое значение составляет 20,49552  угловых секунд (сек) или 0,000099365  радиан (рад) (в J2000 ). ^[9] ${\displaystyle \kappa }$ ${\displaystyle \kappa =\theta -\phi \approx v/c}$ ${\displaystyle v}$ ${\displaystyle c}$

Если предположить, что орбита круговая , годовая аберрация заставляет звезды, находящиеся точно на эклиптике (плоскости орбиты Земли), казаться движущимися вперед и назад по прямой линии, изменяясь на по обе стороны от их положения в рамке Солнца. Звезда, которая находится точно на одном из полюсов эклиптики (под углом 90° от плоскости эклиптики), будет казаться движущейся по окружности радиусом около своего истинного положения, а звезды на промежуточных эклиптических широтах будут казаться движущимися по небольшому эллипсу . ${\displaystyle \kappa }$ ${\displaystyle \kappa }$

Для иллюстрации рассмотрим звезду на северном полюсе эклиптики, видимую наблюдателем из точки на Полярном круге . Такой наблюдатель будет видеть транзит звезды в зените один раз в день (строго говоря, звездные сутки ). Во время мартовского равноденствия орбита Земли переносит наблюдателя в южном направлении, и видимое склонение звезды , таким образом, смещается к югу на угол . Во время сентябрьского равноденствия положение звезды смещается к северу на равную и противоположную величину. В любое солнцестояние смещение по склонению равно 0. И наоборот, величина смещения по прямому восхождению равна 0 в любое равноденствие и максимальна в любое солнцестояние. ${\displaystyle \kappa }$

На самом деле, орбита Земли немного эллиптическая, а не круговая, и ее скорость несколько меняется в течение ее орбиты, что означает, что приведенное выше описание является лишь приблизительным. Аберрация более точно рассчитывается с использованием мгновенной скорости Земли относительно барицентра Солнечной системы. ^[9]

Обратите внимание, что смещение из-за аберрации ортогонально любому смещению из-за параллакса . Если параллакс можно обнаружить, максимальное смещение на юг произойдет в декабре, а максимальное смещение на север — в июне. Именно это, по-видимому, аномальное движение так озадачило ранних астрономов.

Солнечная годовая аберрация

Особым случаем годовой аберрации является почти постоянное отклонение Солнца от его положения в системе покоя Солнца на запад ( если смотреть с Земли), противоположное видимому движению Солнца вдоль эклиптики (которое происходит с запада на восток, если смотреть с Земли). Отклонение, таким образом, заставляет Солнце казаться отстающим (или запаздывающим) от своего положения в системе покоя на эклиптике на позицию или угол . ${\displaystyle \kappa }$ ${\displaystyle \kappa }$

Это отклонение может быть эквивалентно описано как эффект светового времени из-за движения Земли в течение 8,3 минут, которые требуются свету, чтобы пройти путь от Солнца до Земли. Соотношение с имеет вид: [0,000099365 рад / 2 π рад] x [365,25 дx 24 ч/дx 60 мин/ч] = 8,3167 мин ≈ 8 мин 19 сек = 499 сек. Это возможно, поскольку время прохождения солнечного света коротко по сравнению с периодом обращения Земли, поэтому земную систему отсчета можно считать инерциальной. В системе отсчета Земли Солнце движется со средней скоростью v = 29,789 км/с на расстояние ≈ 14 864,7 км за время, необходимое свету, чтобы достичь Земли, ≈ 499 сек для орбиты со средним радиусом = 1 а.е. = 149 597 870,7 км. Это дает угловую поправку ≈ 0,000099364 рад = 20,49539 сек, которую можно решить, дав ≈ 0,000099365 рад = 20,49559 сек, что почти соответствует аберрационной поправке (здесь в радианах, а не в угловых секундах). ${\displaystyle \kappa }$ ${\displaystyle \Delta x=vt}$ ${\displaystyle t=R/c}$ ${\displaystyle R}$ ${\displaystyle \tan(\theta )\approx \theta =\Delta x/R}$ ${\displaystyle \theta =v/c=\kappa }$ ${\displaystyle \kappa }$

Суточная аберрация

Суточная аберрация вызвана скоростью наблюдателя на поверхности вращающейся Земли . Поэтому она зависит не только от времени наблюдения, но также от широты и долготы наблюдателя. Ее эффект намного меньше, чем у годовой аберрации, и составляет всего 0,32 угловых секунды в случае наблюдателя на экваторе , где скорость вращения самая большая. ^[10]

Светское заблуждение

Вековая составляющая аберрации, вызванная движением Солнечной системы в пространстве, была далее разделена на несколько компонентов: аберрация, вызванная движением барицентра Солнечной системы вокруг центра нашей Галактики , аберрация, вызванная движением Галактики относительно Местной группы , и аберрация, вызванная движением Местной группы относительно космического микроволнового фона . ^{[11] : 6} Вековая аберрация влияет на видимые положения звезд и внегалактических объектов. Большая, постоянная часть вековой аберрации не может наблюдаться напрямую, и «было стандартной практикой поглощать этот большой, почти постоянный эффект в сообщаемых» ^{[12] : 1} положениях звезд. ^[13]

Примерно за 200 миллионов лет Солнце совершает оборот вокруг галактического центра, измеренное местоположение которого находится вблизи прямого восхождения (α = 266,4°) и склонения (δ = −29,0°). ^{[12] : 2} Постоянный, ненаблюдаемый эффект движения Солнечной системы вокруг галактического центра был вычислен по-разному как 150 ^{[14] : 743} или 165 ^{[12] : 1} угловых секунд. Другая, наблюдаемая, часть представляет собой ускорение по направлению к галактическому центру приблизительно 2,5 × 10−10 ^м  /с2 ^, что дает изменение аберрации примерно на 5 мкс/год. ^[15] Высокоточные измерения, продолжающиеся в течение нескольких лет, могут наблюдать это изменение вековой аберрации, часто называемое дрейфом вековой аберрации или ускорением Солнечной системы, как малое кажущееся собственное движение . ^{[16] : 1  [12] : 1}

Недавно высокоточная астрометрия внегалактических объектов с использованием как интерферометрии со сверхдлинной базой, так и космической обсерватории Gaia успешно измерила этот небольшой эффект. ^[16] Первое измерение VLBI видимого движения, за период в 20 лет, 555 внегалактических объектов по направлению к центру нашей галактики в экваториальных координатах α = 263° и δ = −20° указало на вековой дрейф аберрации 6,4 ± 1,5 мксв/год. ^{[16] : 1} Более поздние определения с использованием серии измерений VLBI, продолжавшихся почти 40 лет, определили, что вековой дрейф аберрации составил 5,83 ± 0,23 мксв/год в направлении α = 270,2 ± 2,3° и δ = −20,2° ± 3,6°. ^{[11] : 7} Оптические наблюдения, использующие только 33 месяца спутниковых данных Gaia из 1,6 миллиона внегалактических источников, показали ускорение солнечной системы 2,32 ± 0,16 × 10 ⁻¹⁰  м/с ² и соответствующий вековой дрейф аберрации 5,05 ± 0,35 мкс/год в направлении α = 269,1° ± 5,4°, δ = −31,6° ± 4,1°. Ожидается, что более поздние выпуски данных Gaia , включающие около 66 и 120 месяцев данных, уменьшат случайные ошибки этих результатов в 0,35 и 0,15 раза. ^{[17] [18] : 1,14} В последнем издании Международной небесной системы отсчета (ICRF3) была принята рекомендуемая постоянная галактоцентрической аберрации 5,8 мкс/год ^{[12] : 5,7} и рекомендована поправка на вековую аберрацию для получения наивысшей точности позиционирования для времен, отличных от опорной эпохи 2015.0. ^{[11] : 17–19}

Планетарная аберрация

Планетарная аберрация — это комбинация аберрации света (из-за скорости Земли) и поправки на световое время (из-за движения объекта и расстояния), рассчитанная в системе покоя Солнечной системы. Обе определяются в тот момент, когда свет движущегося объекта достигает движущегося наблюдателя на Земле. Она так называется, потому что обычно применяется к планетам и другим объектам в Солнечной системе, движение и расстояние до которых точно известны.

Открытие и первые наблюдения

Открытие аберрации света было совершенно неожиданным, и только благодаря немалой настойчивости и проницательности Брэдли смог объяснить его в 1727 году. Оно возникло из попыток выяснить, обладают ли звезды заметными параллаксами .

Поиск звездного параллакса

Гелиоцентрическая теория Солнечной системы Коперника получила подтверждение в наблюдениях Галилея и Тихо Браге , а также в математических исследованиях Кеплера и Ньютона . ^[19] Еще в 1573 году Томас Диггес предположил, что параллактическое смещение звезд должно происходить в соответствии с гелиоцентрической моделью, и, следовательно, если бы можно было наблюдать звездный параллакс, это помогло бы подтвердить эту теорию. Многие наблюдатели утверждали, что определили такие параллаксы, но Тихо Браге и Джованни Баттиста Риччоли пришли к выводу, что они существуют только в умах наблюдателей и возникают из-за инструментальных и личных ошибок. Однако в 1680 году Жан Пикар в своем «Путешествии в Уранибург » заявил, что в результате десятилетних наблюдений Полярная звезда, демонстрировала изменения в своем положении, составляющие 40″ ежегодно. Некоторые астрономы пытались объяснить это параллаксом, но эти попытки не увенчались успехом, поскольку движение отличалось от того, которое мог бы произвести параллакс. Джон Флемстид , на основе измерений, проведенных в 1689 году и в последующие годы с помощью своего настенного квадранта, также пришел к выводу, что склонение Полярной звезды в июле было на 40″ меньше, чем в сентябре. Роберт Гук в 1674 году опубликовал свои наблюдения γ Дракона , звезды величиной 2 ^м , которая проходит практически над головой на широте Лондона (следовательно, ее наблюдения в значительной степени свободны от сложных поправок, обусловленных атмосферной рефракцией ), и пришел к выводу, что эта звезда была на 23″ севернее в июле, чем в октябре. ^[19]

Наблюдения Джеймса Брэдли

Наблюдения Брэдли за γ Дракона и 35 Жирафа , сведенные Бушем к 1730 году.

Следовательно, когда Брэдли и Сэмюэл Молинье вошли в эту сферу исследований в 1725 году, все еще существовала значительная неопределенность относительно того, наблюдались ли звездные параллаксы или нет, и именно с намерением определенно ответить на этот вопрос они установили большой телескоп в доме Молинье в Кью . ^[4] Они решили повторно исследовать движение γ Draconis с помощью телескопа, сконструированного Джорджем Грэхемом (1675–1751), знаменитым изготовителем инструментов. Он был закреплен на вертикальной дымовой трубе таким образом, чтобы допускать небольшое колебание окуляра, величина которого (т. е. отклонение от вертикали) регулировалась и измерялась путем введения винта и отвеса. ^[19]

Инструмент был установлен в ноябре 1725 года, а наблюдения за γ Draconis проводились, начиная с декабря. Звезда, как было замечено, смещалась на 40" к югу между сентябрем и мартом, а затем меняла свой курс с марта по сентябрь. ^[19] В то же время, 35 Camelopardalis , звезда с прямым восхождением, почти точно противоположным восхождению γ Draconis, была на 19" севернее в начале марта, чем в сентябре. ^[20] Асимметрия этих результатов, которые, как ожидалось, были зеркальными отражениями друг друга, была совершенно неожиданной и необъяснимой существующими теориями.

Ранние гипотезы

Гипотетическое наблюдение γ Дракона, если ее движение вызвано параллаксом.

Гипотетическое наблюдение γ Draconis и 35 Camelopardalis, если их движения были вызваны нутацией.

Брэдли и Молинье обсудили несколько гипотез в надежде найти решение. Поскольку видимое движение, очевидно, не было вызвано ни параллаксом, ни ошибками наблюдений, Брэдли сначала предположил, что оно могло быть вызвано колебаниями ориентации оси Земли относительно небесной сферы — явлением, известным как нутация . 35 Жираф обладал видимым движением, которое могло согласовываться с нутацией, но поскольку его склонение изменялось только на половину от такового у γ Дракона, было очевидно, что нутация не давала ответа ^[21] (однако Брэдли позже обнаружил, что Земля действительно нутирует). ^[22] Он также исследовал возможность того, что движение было вызвано нерегулярным распределением атмосферы Земли , таким образом, включая аномальные изменения показателя преломления, но снова получил отрицательные результаты. ^[21]

19 августа 1727 года Брэдли приступил к дальнейшей серии наблюдений, используя свой собственный телескоп, установленный в приходском доме в Уонстеде . Этот инструмент имел преимущество большего поля зрения, и он смог получить точные положения большого количества звезд в течение примерно двадцати лет. В течение первых двух лет в Уонстеде он установил существование явления аберрации вне всякого сомнения, и это также позволило ему сформулировать набор правил, которые позволили бы рассчитать эффект для любой заданной звезды в указанную дату.

Развитие теории аберрации

Брэдли в конечном итоге разработал свое объяснение аберрации примерно в сентябре 1728 года, и эта теория была представлена ​​Королевскому обществу в середине января следующего года. Одна известная история состояла в том, что он увидел изменение направления флюгера на лодке на Темзе, вызванное не изменением самого ветра, а изменением курса лодки относительно направления ветра. ^[22] Однако в собственном отчете Брэдли об открытии нет записи об этом инциденте, и поэтому он может быть апокрифическим .

В следующей таблице показана величина отклонения от истинного склонения для γ Дракона и направление на плоскостях колюра солнцестояния и нулевого меридиана эклиптики касательной скорости Земли по ее орбите для каждого из четырех месяцев, в которых наблюдаются экстремумы, а также ожидаемое отклонение от истинной эклиптической долготы, если Брэдли измерил ее отклонение от прямого восхождения:

Брэдли предположил, что аберрация света влияет не только на склонение, но и на прямое восхождение, так что звезда на полюсе эклиптики будет описывать небольшой эллипс диаметром около 40", но для простоты он предположил, что это окружность. Поскольку он наблюдал только отклонение по склонению, а не по прямому восхождению, его расчеты максимального отклонения звезды на полюсе эклиптики касаются только ее склонения, которое будет совпадать с диаметром малого круга, описываемого такой звездой. Для восьми различных звезд его расчеты таковы:

На основе этих расчетов Брэдли смог оценить постоянную аберрации в 20,2", что равно 0,00009793 радиан, и с помощью этого смог оценить скорость света в 183 300 миль (295 000 км) в секунду. ^[23] Спроецировав маленький круг на звезду в полюсе эклиптики, он смог упростить расчет соотношения между скоростью света и скоростью годового движения Земли по ее орбите следующим образом:

${\displaystyle \cos \left({\frac {1}{2}}\pi -0.00009793\right)=\sin(0.00009793)={\frac {v}{c}}}$

Таким образом, отношение скорости света к скорости годового движения Земли по ее орбите составляет 10 210 к одному, откуда следует, что свет движется или распространяется от Солнца до Земли за 8 минут 12 секунд. ^[24]

Первоначальной мотивацией поиска звездного параллакса была проверка теории Коперника о вращении Земли вокруг Солнца. Изменение аберрации в течение года демонстрирует относительное движение Земли и звезд.

Ретродикция по поводу аргумента Декарта о скорости света

В предыдущем столетии Рене Декарт утверждал , что если бы свет не был мгновенным, то тени движущихся объектов отставали бы; и если бы время распространения на земные расстояния было бы значительным, то во время лунного затмения Солнце, Земля и Луна были бы не на одной линии из-за часового движения, вопреки наблюдениям. Гюйгенс прокомментировал, что по данным о скорости света Рёмера (дающим время прохождения пути от Земли до Луны туда и обратно всего в несколько секунд) угол отставания был бы незаметен. Они оба упустили из виду ^[25] , что аберрация (как было понято только позже) точно противодействовала бы отставанию, даже если бы оно было большим, делая этот метод затмения полностью нечувствительным к скорости света. (В противном случае методы запаздывания тени можно было бы заставить ощущать абсолютное поступательное движение, вопреки основному принципу относительности .)

Исторические теории аберрации

Явление аберрации стало движущей силой многих физических теорий в течение 200 лет между его наблюдением и объяснением Альбертом Эйнштейном.

Первое классическое объяснение было дано в 1729 году Джеймсом Брэдли, как описано выше, который приписал это конечной скорости света и движению Земли по орбите вокруг Солнца . ^{[3] [4]} Однако это объяснение оказалось неточным, как только волновая природа света была лучше понята, и его исправление стало главной целью теорий светоносного эфира 19-го века . Огюстен-Жан Френель предложил поправку, обусловленную движением среды (эфира), через которую распространяется свет, известную как «частичное увлечение эфиром» . Он предположил, что объекты частично увлекают эфир вместе с собой по мере своего движения, и это стало общепринятым объяснением аберрации на некоторое время. Джордж Стокс предложил похожую теорию, объяснив, что аберрация возникает из-за потока эфира, вызванного движением Земли. Накопленные доказательства против этих объяснений, в сочетании с новым пониманием электромагнитной природы света, привели Хендрика Лоренца к разработке электронной теории , которая включала неподвижный эфир, и он объяснил, что объекты сокращаются в длине, когда они движутся через эфир. Мотивированный этими предыдущими теориями, Альберт Эйнштейн затем разработал теорию специальной теории относительности в 1905 году, которая обеспечивает современный учет аберрации.

Классическое объяснение Брэдли

Рисунок 2: По мере того, как свет распространяется по телескопу, телескоп движется, требуя наклона телескопа, который зависит от скорости света. Видимый угол звезды φ отличается от ее истинного угла θ .

Брэдли предложил объяснение в терминах корпускулярной теории света, в которой свет состоит из частиц. ^[1] Его классическое объяснение апеллирует к движению Земли относительно пучка частиц света, движущихся с конечной скоростью, и разрабатывается в системе отсчета Солнца, в отличие от классического вывода, приведенного выше.

Рассмотрим случай, когда далекая звезда неподвижна относительно Солнца, и звезда находится очень далеко, так что параллакс можно игнорировать. В системе покоя Солнца это означает, что свет от звезды распространяется по параллельным путям к земному наблюдателю и достигает его под одним и тем же углом независимо от того, где находится Земля на своей орбите. Предположим, что звезда наблюдается на Земле с помощью телескопа, идеализированного как узкая трубка. Свет входит в трубку от звезды под углом и распространяется со скоростью, требующей времени, чтобы достичь дна трубки, где он обнаруживается. Предположим, что наблюдения проводятся с Земли, которая движется со скоростью . Во время прохождения света трубка перемещается на расстояние . Следовательно, для того, чтобы частицы света достигли дна трубки, трубка должна быть наклонена под углом, отличным от , в результате чего видимое положение звезды находится под углом . По мере того, как Земля движется по своей орбите, она меняет направление, поэтому изменяется в зависимости от времени года, когда производится наблюдение. Видимый угол и истинный угол связаны с помощью тригонометрии следующим образом: ${\displaystyle \theta }$ ${\displaystyle c}$ ${\displaystyle h/c}$ ${\displaystyle v}$ ${\displaystyle vh/c}$ ${\displaystyle \phi }$ ${\displaystyle \theta }$ ${\displaystyle \phi }$ ${\displaystyle \phi }$

${\displaystyle \tan(\phi )={\frac {h\sin(\theta )}{hv/c+h\cos(\theta )}}={\frac {\sin(\theta )}{v/c+\cos(\theta )}}}$.

В случае это дает . Хотя это отличается от более точного релятивистского результата, описанного выше, в пределе малого угла и малой скорости они примерно одинаковы, в пределах погрешности измерений времен Брэдли. Эти результаты позволили Брэдли сделать одно из самых ранних измерений скорости света . [ ^{24] [26]} ${\displaystyle \theta =90^{\circ }}$ ${\displaystyle \tan(\theta -\phi )=v/c}$

Светоносный эфир

Юнг рассуждал, что аберрацию можно объяснить только если эфир неподвижен в рамке Солнца. Слева звездная аберрация возникает, если предполагается неподвижный эфир, показывая, что телескоп должен быть наклонен. Справа аберрация исчезает, если эфир движется вместе с телескопом, и телескоп не нужно наклонять.

В начале девятнадцатого века волновая теория света была заново открыта, и в 1804 году Томас Янг адаптировал объяснение Брэдли для корпускулярного света к волнообразному свету, проходящему через среду, известную как светоносный эфир. Его рассуждения были такими же, как у Брэдли, но они требовали, чтобы эта среда была неподвижна в системе отсчета Солнца и должна была пройти через Землю без изменений, в противном случае среда (и, следовательно, свет) двигалась бы вместе с Землей, и никакой аберрации не наблюдалось бы. ^[27] Он писал:

Рассмотрев явления аберрации звезд, я склонен полагать, что светоносный эфир пронизывает субстанцию ​​всех материальных тел с небольшим сопротивлением или вообще без него, возможно, так же свободно, как ветер проходит через рощу деревьев.

—  Томас Янг, 1804 ^[1]

Однако вскоре стало ясно, что теория Юнга не может объяснить аберрацию, когда присутствуют материалы с невакуумным показателем преломления . Важным примером является телескоп, заполненный водой. Скорость света в таком телескопе будет меньше, чем в вакууме, и определяется как , а не как , где показатель преломления воды. Таким образом, по рассуждениям Брэдли и Янга, угол аберрации определяется как ${\displaystyle c/n}$ ${\displaystyle c}$ ${\displaystyle n}$

${\displaystyle \tan(\phi )={\frac {\sin(\theta )}{v/(c/n)+\cos(\theta )}}}$.

который предсказывает зависящий от среды угол аберрации. Когда учитывается рефракция в объективе телескопа, этот результат еще больше отклоняется от результата для вакуума. В 1810 году Франсуа Араго провел аналогичный эксперимент и обнаружил, что аберрация не зависит от среды в телескопе, что предоставило убедительные доказательства против теории Юнга. Этот эксперимент впоследствии был проверен многими другими в последующие десятилетия, наиболее точно Эйри в 1871 году с тем же результатом. ^[27]

Модели сопротивления эфира

Эфирное сопротивление Френеля

В 1818 году Огюстен Френель разработал модифицированное объяснение для учета водяного телескопа и других явлений аберрации. Он объяснил, что эфир, как правило, находится в состоянии покоя в системе отсчета Солнца, но объекты частично увлекают эфир за собой по мере своего движения. То есть эфир в объекте с показателем преломления, движущемся со скоростью , частично увлекается со скоростью, увлекающей за собой свет. Этот фактор известен как «коэффициент увлечения Френеля». Этот эффект увлечения, наряду с преломлением в объективе телескопа, компенсирует более медленную скорость света в водяном телескопе в объяснении Брэдли. ^[a] С этой модификацией Френель получил вакуумный результат Брэдли даже для невакуумных телескопов, а также смог предсказать многие другие явления, связанные с распространением света в движущихся телах. Коэффициент увлечения Френеля стал доминирующим объяснением аберрации на следующие десятилетия. ${\displaystyle n}$ ${\displaystyle v}$ ${\displaystyle (1-1/n^{2})v}$

Концептуальная иллюстрация теории увлечения эфира Стокса. В системе покоя Солнца Земля движется вправо через эфир, в котором она индуцирует локальный ток. Луч света (красный), идущий от вертикали, увлекается и наклоняется из-за потока эфира.

Эфирное сопротивление Стокса

Однако тот факт, что свет поляризован (открытый самим Френелем), привел таких ученых, как Коши и Грин, к убеждению, что эфир был полностью неподвижным упругим твердым телом в отличие от жидкого эфира Френеля. Таким образом, вновь возникла необходимость в объяснении аберрации, согласующейся как с предсказаниями Френеля (и наблюдениями Араго), так и с поляризацией.

В 1845 году Стокс предложил «замазкообразный» эфир, который действует как жидкость в больших масштабах, но как твердое тело в малых масштабах, таким образом поддерживая как поперечные колебания, необходимые для поляризованного света, так и поток эфира, необходимый для объяснения аберрации. Сделав только предположения, что жидкость является безвихревой и что граничные условия потока таковы, что эфир имеет нулевую скорость вдали от Земли, но движется со скоростью Земли на ее поверхности и внутри нее, он смог полностью объяснить аберрацию. ^[b] Скорость эфира вне Земли будет уменьшаться как функция расстояния от Земли, поэтому световые лучи от звезд будут постепенно увлекаться по мере приближения к поверхности Земли. Движение Земли не будет зависеть от эфира из-за парадокса Даламбера .

Теории Френеля и Стокса были популярны. Однако вопрос об аберрации был отложен в сторону в течение большей части второй половины XIX века, поскольку фокус исследований переключился на электромагнитные свойства эфира.

Сокращение длины Лоренца

В 1880-х годах, когда электромагнетизм был лучше понят, интерес снова обратился к проблеме аберрации. К этому времени были известны недостатки как теорий Френеля, так и Стокса. Теория Френеля требовала, чтобы относительная скорость эфира и материи была разной для света разных цветов, и было показано, что граничные условия, которые Стокс предположил в своей теории, несовместимы с его предположением о безвихревом потоке. ^{[1] [27] [28]} В то же время современные теории электромагнитного эфира вообще не могли объяснить аберрацию. Многие ученые, такие как Максвелл , Хевисайд и Герц, безуспешно пытались решить эти проблемы, включив теории Френеля или Стокса в новые электромагнитные законы Максвелла .

Хендрик Лоренц потратил значительные усилия в этом направлении. После десятилетней работы над этой проблемой проблемы с теорией Стокса заставили его отказаться от нее и последовать предложению Френеля о (в основном) неподвижном эфире (1892, 1895). Однако в модели Лоренца эфир был полностью неподвижен, как электромагнитные эфиры Коши, Грина и Максвелла и в отличие от эфира Френеля. Он получил коэффициент увлечения Френеля из модификаций электромагнитной теории Максвелла, включая модификацию временных координат в движущихся системах отсчета («местное время»). Чтобы объяснить эксперимент Майкельсона–Морли (1887), который, по-видимому, противоречил теориям неподвижного эфира как Френеля, так и Лоренца и, по-видимому, подтвердил полное увлечение эфира Стокса, Лоренц выдвинул теорию (1892), что объекты претерпевают « сокращение длины » в раз в направлении их движения через эфир. Таким образом, аберрация (и все связанные с ней оптические явления) могут быть учтены в контексте неподвижного эфира. Теория Лоренца стала основой для многих исследований в следующем десятилетии и далее. Ее предсказания относительно аберрации идентичны предсказаниям релятивистской теории. ^{[27] [29]} ${\displaystyle {\sqrt {1-v^{2}/c^{2}}}}$

Специальная теория относительности

Теория Лоренца хорошо соответствовала эксперименту, но была сложной и делала много необоснованных физических предположений о микроскопической природе электромагнитных сред. В своей теории специальной теории относительности 1905 года Альберт Эйнштейн переосмыслил результаты теории Лоренца в гораздо более простой и естественной концептуальной структуре, которая избавилась от идеи эфира. Его вывод приведен выше , и теперь это общепринятое объяснение. Роберт С. Шенкленд сообщил о некоторых беседах с Эйнштейном, в которых Эйнштейн подчеркивал важность аберрации: ^[30]

Он продолжил говорить, что экспериментальные результаты, которые оказали на него наибольшее влияние, были наблюдения за аберрацией звезд и измерения Физо скорости света в движущейся воде. «Их было достаточно», — сказал он.

Другими важными мотивами развития Эйнштейном теории относительности были проблема движущегося магнита и проводника и (косвенно) эксперименты по отрицательному эфирному дрейфу, уже упомянутые им во введении к его первой статье по теории относительности. Эйнштейн написал в заметке в 1952 году: ^[5]

На мои собственные мысли более косвенно повлиял знаменитый эксперимент Майкельсона-Морли. Я узнал о нем из новаторского исследования Лоренца по электродинамике движущихся тел (1895), о котором я знал до создания специальной теории относительности. Основное предположение Лоренца о покоящемся эфире не казалось мне непосредственно убедительным, поскольку оно приводило к [вычеркнуто: мне искусственно выглядящему] интерпретации эксперимента Майкельсона-Морли, которая [вычеркнуто: не убедила меня] казалась мне неестественной. Мой прямой путь к sp. th. rel. в основном определялся убеждением, что электродвижущая сила, индуцируемая в проводнике, движущемся в магнитном поле, есть не что иное, как электрическое поле. Но результат эксперимента Физо и явление аберрации также направляли меня.

Хотя результат Эйнштейна совпадает с исходным уравнением Брэдли, за исключением дополнительного множителя , результат Брэдли не просто дает классический предел релятивистского случая, в том смысле, что он дает неверные предсказания даже при низких относительных скоростях. Объяснение Брэдли не может объяснить такие ситуации, как водный телескоп, или многие другие оптические эффекты (например, интерференцию), которые могут возникнуть внутри телескопа. Это происходит потому, что в системе отсчета Земли оно предсказывает, что направление распространения светового луча в телескопе не является нормальным к волновым фронтам луча, что противоречит теории электромагнетизма Максвелла . Оно также не сохраняет скорость света c между кадрами. Однако Брэдли правильно сделал вывод, что эффект был вызван относительными скоростями. ${\displaystyle \gamma }$

Смотрите также

• Видимое место
• Звездный параллакс
• Астрономическая нутация
• Правильное движение
• Хронология электромагнетизма и классической оптики
• Релятивистская аберрация

Примечания

1. Более подробно Френель объясняет, что входящий свет угла сначала преломляется на конце телескопа, в новый угол внутри телескопа. Это можно объяснить законом Снеллиуса , давая . Затем необходимо учесть сопротивление. Без сопротивления компоненты x и y света в телескопе равны и , но сопротивление изменяет компонент x на , если Земля движется со скоростью . Если есть угол и есть скорость света с этими компонентами скорости, то по рассуждениям Брэдли где есть измененная длина пути через воду, а t есть время, необходимое свету, чтобы пройти расстояние h, . Решив эти уравнения для в терминах получаем вакуумный результат Брэдли. ${\displaystyle \theta }$ ${\displaystyle \psi }$ ${\displaystyle \sin(\theta -\phi )=n\sin(\psi -\phi )}$ ${\displaystyle (c/n)\sin(\psi )}$ ${\displaystyle (c/n)\cos(\psi )}$ ${\displaystyle (c/n)\cos(\psi )-(1-1/n^{2})v}$ ${\displaystyle v}$ ${\displaystyle \alpha }$ ${\displaystyle v_{l}}$ ${\displaystyle \tan(\phi )={\frac {h\sin(\alpha )}{vt+h\cos(\alpha )}}}$ ${\displaystyle h}$ ${\displaystyle t=h/v_{l}}$ ${\displaystyle \phi }$ ${\displaystyle \theta }$

2. 

   Распространяющийся волновой фронт, движущийся через эфир.

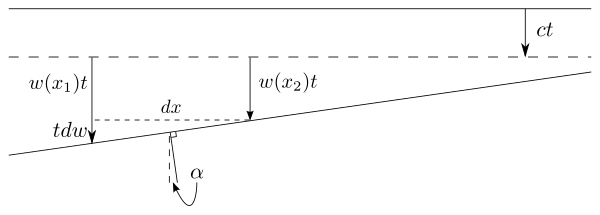
   Вывод Стокса можно обобщить следующим образом: Рассмотрим волновой фронт, движущийся в направлении z вниз. Допустим, эфир имеет поле скорости как функцию . Теперь, движение эфира в направлениях x и y не влияет на волновой фронт, но движение в направлении z продвигает его вперед (в дополнение к величине, на которую он продвигается со скоростью c). Если скорость z эфира изменяется в пространстве, например, если она медленнее для более высоких x, как показано на рисунке, то волновой фронт становится наклонным на угол . Теперь, скажем, за время t волновой фронт переместился на пролет (предполагая, что скорость эфира пренебрежимо мала по сравнению со скоростью света). Затем на каждом расстоянии, которое спускается луч, он изгибается на угол , и поэтому общий угол, на который он изменился после прохождения через всю жидкость, равен ${\displaystyle u,v,w}$ ${\displaystyle x,y,z}$ ${\displaystyle \tan(\alpha )=tdw/dx}$ ${\displaystyle dz\approx ct}$ ${\displaystyle dz}$ ${\displaystyle \alpha \approx (dw/dx)(dz/c)}$

   ${\displaystyle \alpha \approx {\frac {1}{c}}\int {\frac {\partial w}{\partial x}}dz}$

   Если жидкость безвихревая, она будет удовлетворять уравнениям Коши–Римана , одно из которых имеет вид

   ${\displaystyle {\frac {\partial w}{\partial x}}={\frac {\partial u}{\partial z}}}$.

   Вставка этого в предыдущий результат дает угол аберрации , где s представляет собой компонент x скорости эфира в начале и конце луча. Вдали от Земли эфир имеет нулевую скорость, поэтому и на поверхности Земли он имеет скорость Земли . Таким образом, мы в конечном итоге получаем ${\displaystyle \alpha =(u_{2}-u_{1})/c}$ ${\displaystyle u}$ ${\displaystyle u_{2}=0}$ ${\displaystyle v}$

   ${\displaystyle \alpha \approx {\frac {v}{c}}}$

   что является известным результатом аберрации.

Ссылки

1. Шаффнер, Кеннет Ф. (1972). Теории эфира девятнадцатого века . Оксфорд: Pergamon Press. С. 99–117 и 255–273. ISBN 0-08-015674-6.
2. Уильямс, MEW (1979). «Предполагаемое измерение Флемстидом годового параллакса для Полярной звезды». Журнал истории астрономии . 10 (2): 102–116. Bibcode : 1979JHA....10..102W. doi : 10.1177/002182867901000203. S2CID  118565124.
3. Брэдли, Джеймс (1727–1728). «Письмо преподобного мистера Джеймса Брэдли Сэвильяна, профессора астрономии в Оксфорде и члена Королевского общества, доктору Эдмонду Галлею, астроному. Рег. и т. д., дающее отчет о новом открытом движении неподвижных звезд». Phil. Trans. R. Soc . 35 (406): 637–661. Bibcode : 1727RSPT...35..637B. doi : 10.1098/rstl.1727.0064 .
4. Хиршфельд, Алан (2001). Параллакс: гонка за измерение космоса . Нью-Йорк, Нью-Йорк: Генри Холт. ISBN 0-8050-7133-4.
5. Norton, John D. (2004). "Исследования Эйнштейна по галилеевской ковариантной электродинамике до 1905 года". Архив для History of Exact Sciences . 59 (1): 45–105. Bibcode :2004AHES...59...45N. doi :10.1007/s00407-004-0085-6. S2CID  17459755. Архивировано из оригинала 2009-01-11.
6. Ричард А. Молд (2001). Основные положения теории относительности (2-е изд.). Springer. стр. 8. ISBN 0-387-95210-1.
7. На самом деле источник света не обязательно должен быть неподвижным, рассмотрим, например, затменные двойные звезды: они вращаются с высокой скоростью (и постоянно меняющимися и разными векторами скорости) вокруг друг друга, но они все время выглядят как одна точка.
8. US Nautical Almanac Office (21 марта 2014 г.). "Глоссарий". Астрономический альманах на 2015 год и его дополнение, The Astronomical Almanac Online. Вашингтон, округ Колумбия: Типография правительства США (опубликовано в 2014 г.). стр. M1. ISBN 9780707741499.
9. Kovalevsky, Jean & Seidelmann, P. Kenneth (2004). Основы астрометрии . Кембридж: Cambridge University Press . ISBN 0-521-64216-7.
10. Ньюкомб, Саймон (1960). Компендиум сферической астрономии . Macmillan, 1906 – переиздано Dover .
11. Charlot, P.; Jacobs, CS; Gordon, D.; Lambert, S.; et al. (2020). "Третья реализация Международной небесной системы отсчета с помощью интерферометрии с очень длинной базой". Астрономия и астрофизика . 644 : A159. arXiv : 2010.13625 . Bibcode : 2020A&A...644A.159C. doi : 10.1051/0004-6361/202038368. S2CID  225068756.
12. MacMillan, DS; Fey, A.; Gipson, JM; et al. (2019). "Галактоцентрическое ускорение в анализе VLBI". Astronomy and Astrophysics . 630 : A93. Bibcode : 2019A&A...630A..93M. doi : 10.1051/0004-6361/201935379. S2CID  198471325.
13. Хагихара, Юсукэ (1933). «О теории вековой аберрации». Труды физико-математического общества Японии . 3-я серия. 15 (3–6): 175. doi :10.11429/ppmsj1919.15.3-6_155. исправление положения звезд с вековой аберрацией вовсе не обязательно и даже неудобно, пока движение Солнца остается равномерным и прямолинейным.
14. Ковалевский, Дж. (2003). «Аберрация в собственных движениях». Астрономия и астрофизика . 404 (2): 743–747. Bibcode :2003A&A...404..743K. doi : 10.1051/0004-6361:20030560 .
15. Копейкин, С.; Макаров, В. (2006). «Астрометрические эффекты вековой аберрации». The Astronomical Journal (США) . 131 (3): 1471–1478. arXiv : astro-ph/0508505 . Bibcode : 2006AJ....131.1471K. doi : 10.1086/500170 .
16. Титов, О.; Ламберт, СБ; Гонтье, А.-М. (2011). "VLBI-измерение векового дрейфа аберрации". Астрономия и астрофизика . 529 : A91. arXiv : 1009.3698 . Bibcode : 2011A&A...529A..91T. doi : 10.1051/0004-6361/201015718. S2CID  119305429.
17. "Измерение Gaia ускорения Солнечной системы относительно далекой Вселенной". esa.int . Европейское космическое агентство . 3 декабря 2020 г. Получено 14 сентября 2022 г.
18. Gaia Collaboration; Klioner, SA; et al. (2021). "Gaia Early Data Release 3: Acceleration of the Solar System from Gaia astrometry". Астрономия и астрофизика . 649 : A9. arXiv : 2012.02036 . Bibcode : 2021A&A...649A...9G. doi : 10.1051/0004-6361/202039734.
19. Эппенштейн (1911), стр. 54.
20. Брэдли, Джеймс; Риго, Стивен Питер (1832). Разные труды и переписка преподобного Джеймса Брэдли, доктора богословия, члена Королевского общества Оксфорда: University Press. стр. 11.
21. Eppenstein (1911), стр. 55.
22. Берри, Артур (1961) [1898]. Краткая история астрономии . Дувр . ISBN 9780486202105.
23. Hoiberg, Dale H., ред. (2010). "аберрация, константа" . Encyclopaedia Britannica . Том I: A-ak Bayes (15-е изд.). Чикаго, Иллинойс: Encyclopaedia Britannica Inc., стр. 30. ISBN 978-1-59339-837-8.
24. Джеймс Брэдли (1729). «Отчет о новом открытом движении неподвижных звезд». Philosophical Transactions of the Royal Society . 35 : 637–661. doi : 10.1098/rstl.1727.0064 .
25. Сакеллариадис, Спирос (1982). «Экспериментальное доказательство Декарта бесконечной скорости света и ответ Гюйгенса». Архив истории точных наук . 26 (1): 1–12. doi :10.1007/BF00348308. ISSN  0003-9519. JSTOR  41133639. S2CID  118187860.
26. Encyclopaedia Britannica Архивировано 11 ноября 2013 г. на Wayback Machine
27. Уиттекер, Эдмунд Тейлор (1910). История теорий эфира и электричества (1-е изд.). Дублин: Longman, Green and Co. Архивировано из оригинала 2016-02-15.
    Уиттекер, Эдмунд Тейлор (1953). История теорий эфира и электричества (2-е изд.). Т. Нельсон.
28. Янссен, Мишель и Стахель, Джон (2010). "Оптика и электродинамика движущихся тел" (PDF) . В Джоне Стахеле (ред.). Going Critical . Springer. ISBN 978-1-4020-1308-9. Архивировано (PDF) из оригинала 2022-10-09.
29. Дарриголь, Оливье (2000). Электродинамика от Ампера до Эйнштейна . Оксфорд: Clarendon Press. ISBN 0-19-850594-9.
30. Шенкленд, RS (1963). «Беседы с Альбертом Эйнштейном». Американский журнал физики . 31 (1): 47–57. Bibcode : 1963AmJPh..31...47S. doi : 10.1119/1.1969236.

•  В этой статье использован текст из публикации, которая сейчас находится в общественном достоянии :  Эппенштейн, Отто (1911). «Аберрация». Encyclopaedia Britannica . Т. 1 (11-е изд.). С. 54–61.

Дальнейшее чтение

• П. Кеннет Зайдельман (ред.), Пояснительное приложение к Астрономическому альманаху (University Science Books, 1992), 127–135, 700.
• Стивен Питер Риго , «Различные труды и переписка преподобного Джеймса Брэдли», DDFRS (1832).
• Чарльз Хаттон , Математический и философский словарь (1795).
• Х. Х. Тернер, Астрономическое открытие (1904).
• Томас Симпсон , «Очерки нескольких любопытных и полезных предметов в спекулятивной и смешанной математике» (1740).
• de: Август Людвиг Буш, Обработка наблюдений, сделанных Брэдли в Кью и Ванстеде, для определения величин аберрации и нутации (1838).

Внешние ссылки

• Кортни Селигман о наблюдениях Брэдли