Адаптивный фильтр

Система с самооптимизирующейся передаточной функцией

Адаптивный фильтр — это система с линейным фильтром , которая имеет передаточную функцию , управляемую переменными параметрами, и средства для настройки этих параметров в соответствии с алгоритмом оптимизации . Из-за сложности алгоритмов оптимизации почти все адаптивные фильтры являются цифровыми фильтрами . Адаптивные фильтры требуются для некоторых приложений, поскольку некоторые параметры желаемой операции обработки (например, расположение отражающих поверхностей в реверберирующем пространстве ) заранее неизвестны или изменяются. Адаптивный фильтр с замкнутым контуром использует обратную связь в виде сигнала ошибки для уточнения своей передаточной функции.

В общем, адаптивный процесс с замкнутым контуром подразумевает использование функции стоимости , которая является критерием оптимальной производительности фильтра, для подачи в алгоритм, который определяет, как модифицировать передаточную функцию фильтра, чтобы минимизировать стоимость на следующей итерации. Наиболее распространенной функцией стоимости является средний квадрат сигнала ошибки.

С ростом мощности цифровых сигнальных процессоров адаптивные фильтры стали гораздо более распространенными и теперь регулярно используются в таких устройствах, как мобильные телефоны и другие устройства связи, видеокамеры и цифровые фотоаппараты, а также в медицинском мониторинговом оборудовании.

Пример заявки

Запись сердечного ритма (ЭКГ ) может быть искажена шумом от сети переменного тока . Точная частота питания и ее гармоники могут меняться в зависимости от момента.

Одним из способов устранения шума является фильтрация сигнала с помощью режекторного фильтра на частоте сети и вблизи нее, однако это может существенно ухудшить качество ЭКГ, поскольку сердечный ритм, скорее всего, также будет иметь частотные компоненты в отклоняемом диапазоне.

Чтобы обойти эту потенциальную потерю информации, можно использовать адаптивный фильтр. Адаптивный фильтр будет принимать входные данные как от пациента, так и от сети, и, таким образом, сможет отслеживать фактическую частоту шума по мере ее колебаний и вычитать шум из записи. Такая адаптивная техника обычно позволяет использовать фильтр с меньшим диапазоном отклонения, что означает, в данном случае, что качество выходного сигнала будет более точным для медицинских целей. ^{[1] [2]}

Блок-схема

Идея адаптивного фильтра с замкнутым контуром заключается в том, что переменный фильтр настраивается до тех пор, пока ошибка (разница между выходом фильтра и желаемым сигналом) не будет минимизирована. Фильтр наименьших средних квадратов (LMS) и рекурсивный фильтр наименьших квадратов (RLS) являются типами адаптивного фильтра.

Адаптивный фильтр. k = номер образца, x = опорный вход, X = набор последних значений x, d = желаемый вход, W = набор коэффициентов фильтра, ε = выход ошибки, f = импульсная характеристика фильтра, * = свертка, Σ = суммирование, верхний ящик = линейный фильтр, нижний ящик = алгоритм адаптации

Адаптивный фильтр, компактное представление. k = номер выборки, x = опорный вход, d = желаемый вход, ε = выход ошибки, f = импульсная характеристика фильтра, Σ = суммирование, box = линейный фильтр и алгоритм адаптации.

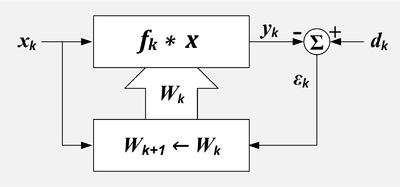
Для адаптивного фильтра есть два входных сигнала: и которые иногда называют первичным входом и опорным входом соответственно. ^[3] Алгоритм адаптации пытается отфильтровать опорный вход в копию желаемого входа путем минимизации остаточного сигнала, . Если адаптация прошла успешно, выход фильтра фактически является оценкой желаемого сигнала. ${\displaystyle d_{k}}$ ${\displaystyle x_{k}}$ ${\displaystyle \epsilon _{k}}$ ${\displaystyle y_{k}}$

${\displaystyle d_{k}}$который включает в себя полезный сигнал плюс нежелательные помехи и

${\displaystyle x_{k}}$который включает в себя сигналы, которые коррелируют с некоторыми нежелательными помехами в . ${\displaystyle d_{k}}$

k представляет собой номер дискретной выборки.

Фильтр управляется набором L+1 коэффициентов или весов.

${\displaystyle \mathbf {W} _{k}=\left[w_{0k},\,w_{1k},\,...,\,w_{Lk}\right]^{T}}$представляет собой набор или вектор весов, которые управляют фильтром в момент времени выборки k.

где относится к '-му весу в k-й момент времени. ${\displaystyle w_{lk}}$ ${\displaystyle l}$

${\displaystyle \mathbf {\Delta W} _{k}}$представляет собой изменение весов, которое происходит в результате корректировок, вычисленных во время выборки k.

Эти изменения будут применены после времени выборки k и до того, как они будут использованы во время выборки k+1.

Выход обычно есть, но это может быть или даже могут быть коэффициенты фильтра. ^[4] (Widrow) ${\displaystyle \epsilon _{k}}$ ${\displaystyle y_{k}}$

Входные сигналы определяются следующим образом:

${\displaystyle d_{k}=g_{k}+u_{k}+v_{k}}$

${\displaystyle x_{k}=g_{k}^{'}+u_{k}^{'}+v_{k}^{'}}$

где:

g = желаемый сигнал,

g ' = сигнал, который коррелирует с желаемым сигналом g ,

u = нежелательный сигнал, который добавляется к g , но не коррелирует с g или g '

u ' = сигнал, который коррелирует с нежелательным сигналом u , но не коррелирует с g или g ' ,

v = нежелательный сигнал (обычно случайный шум), не коррелирующий с g , g ' , u , u ' или v ' ,

v ' = нежелательный сигнал (обычно случайный шум), не коррелирующий с g , g ' , u , u ' или v .

Выходные сигналы определяются следующим образом:

${\displaystyle y_{k}={\hat {g}}_{k}+{\hat {u}}_{k}+{\hat {v}}_{k}}$

${\displaystyle \epsilon _{k}=d_{k}-y_{k}}$.

где:

${\displaystyle {\hat {g}}}$= выход фильтра, если на входе был только g ' ,

${\displaystyle {\hat {u}}}$= выход фильтра, если на входе был только u ' ,

${\displaystyle {\hat {v}}}$= выходной сигнал фильтра, если на входе был только v ' .

Фильтр FIR с отводной линией задержки

Если переменный фильтр имеет структуру конечной импульсной характеристики (КИХ) с отводной линией задержки , то импульсная характеристика равна коэффициентам фильтра. Выход фильтра определяется как

${\displaystyle y_{k}=\sum _{l=0}^{L}w_{lk}\ x_{(k-l)}={\hat {g}}_{k}+{\hat {u}}_{k}+{\hat {v}}_{k}}$

где относится к '-му весу в k-й момент времени. ${\displaystyle w_{lk}}$ ${\displaystyle l}$

Идеальный случай

В идеальном случае . Все нежелательные сигналы в представлены . состоит полностью из сигнала, коррелирующего с нежелательным сигналом в . ${\displaystyle v\equiv 0,v'\equiv 0,g'\equiv 0}$ ${\displaystyle d_{k}}$ ${\displaystyle u_{k}}$ ${\displaystyle \ x_{k}}$ ${\displaystyle u_{k}}$

Выход переменного фильтра в идеальном случае равен

${\displaystyle y_{k}={\hat {u}}_{k}}$.

Сигнал ошибки или функция стоимости — это разница между и ${\displaystyle d_{k}}$ ${\displaystyle y_{k}}$

${\displaystyle \epsilon _{k}=d_{k}-y_{k}=g_{k}+u_{k}-{\hat {u}}_{k}}$. Желаемый сигнал g _k проходит без изменений.

Сигнал ошибки минимизируется в среднеквадратичном смысле, когда минимизируется. Другими словами, является наилучшей среднеквадратичной оценкой . В идеальном случае и , и все, что остается после вычитания, это , что является неизменным желаемым сигналом со всеми удаленными нежелательными сигналами. ${\displaystyle \epsilon _{k}}$ ${\displaystyle [u_{k}-{\hat {u}}_{k}]}$ ${\displaystyle {\hat {u}}_{k}}$ ${\displaystyle u_{k}}$ ${\displaystyle u_{k}={\hat {u}}_{k}}$ ${\displaystyle \epsilon _{k}=g_{k}}$ ${\displaystyle g}$

Компоненты сигнала на опорном входе

В некоторых ситуациях опорный вход включает компоненты полезного сигнала. Это означает, что g' ≠ 0. ${\displaystyle x_{k}}$

Идеальное подавление нежелательных помех в данном случае невозможно, но улучшение соотношения сигнал/помеха возможно. Выход будет

${\displaystyle \epsilon _{k}=d_{k}-y_{k}=g_{k}-{\hat {g}}_{k}+u_{k}-{\hat {u}}_{k}}$. Желаемый сигнал будет изменен (обычно уменьшен).

Отношение выходного сигнала к помехам определяется простой формулой, называемой инверсией мощности .

${\displaystyle \rho _{\mathsf {out}}(z)={\frac {1}{\rho _{\mathsf {ref}}(z)}}}$.

где

${\displaystyle \rho _{\mathsf {out}}(z)\ }$= отношение выходного сигнала к помехам.

${\displaystyle \rho _{\mathsf {ref}}(z)\ }$= отношение опорного сигнала к помехам.

${\displaystyle z\ }$= частота в z-области.

Эта формула означает, что отношение выходного сигнала к помехам на определенной частоте является обратной величиной отношения опорного сигнала к помехам. ^[5]

Пример: В ресторане быстрого питания есть окно для подъезда. Перед тем как подойти к окну, клиенты делают заказ, говоря в микрофон. Микрофон также улавливает шум от двигателя и окружающей среды. Этот микрофон обеспечивает первичный сигнал. Мощность сигнала от голоса клиента и мощность шума от двигателя равны. Сотрудникам ресторана сложно понять клиента. Чтобы уменьшить количество помех в основном микрофоне, второй микрофон расположен там, где он должен улавливать звуки от двигателя. Он также улавливает голос клиента. Этот микрофон является источником опорного сигнала. В этом случае шум двигателя в 50 раз мощнее голоса клиента. После того, как компенсатор сойдется, соотношение первичного сигнала к помехам улучшится с 1:1 до 50:1.

Адаптивный линейный комбайнер

Адаптивный линейный объединитель, демонстрирующий объединитель и процесс адаптации. k = номер выборки, n = индекс входной переменной, x = опорные входы, d = желаемый вход, W = набор коэффициентов фильтра, ε = выход ошибки, Σ = суммирование, верхний ящик = линейный объединитель, нижний ящик = алгоритм адаптации.

Адаптивный линейный объединитель, компактное представление. k = номер выборки, n = индекс входной переменной, x = опорные входы, d = желаемый вход, ε = выход ошибки, Σ = суммирование.

Адаптивный линейный комбайнер (ALC) напоминает адаптивный фильтр FIR с отводной линией задержки, за исключением того, что между значениями X не предполагается никакой связи. Если бы значения X были с выходов отводной линии задержки, то комбинация отводной линии задержки и ALC составляла бы адаптивный фильтр. Однако значения X могли бы быть значениями массива пикселей. Или они могли бы быть выходами нескольких отводных линий задержки. ALC находит применение в качестве адаптивного формирователя луча для массивов гидрофонов или антенн.

${\displaystyle y_{k}=\sum _{l=0}^{L}w_{lk}\ x_{lk}=\mathbf {W} _{k}^{T}\mathbf {x} _{k}}$

где относится к '-му весу в k-й момент времени. ${\displaystyle w_{lk}}$ ${\displaystyle l}$

Алгоритм системы управления обучением

Если переменный фильтр имеет структуру FIR с отводной линией задержки, то алгоритм обновления LMS особенно прост. Обычно после каждой выборки коэффициенты FIR-фильтра корректируются следующим образом: ^[6]

для ${\displaystyle l=0\dots L}$

${\displaystyle w_{l,k+1}=w_{lk}+2\mu \ \epsilon _{k}\ x_{k-l}}$

μ называется коэффициентом сходимости .

Алгоритм LMS не требует, чтобы значения X имели какую-либо определенную связь; поэтому его можно использовать для адаптации линейного объединителя, а также фильтра FIR. В этом случае формула обновления записывается как:

${\displaystyle w_{l,k+1}=w_{lk}+2\mu \ \epsilon _{k}\ x_{lk}}$

Эффект алгоритма LMS заключается в том, чтобы в каждый момент времени k вносить небольшое изменение в каждый вес. Направление изменения таково, что оно уменьшило бы ошибку, если бы оно было применено в момент времени k. Величина изменения каждого веса зависит от μ, связанного значения X и ошибки в момент времени k. Веса, вносящие наибольший вклад в выходной сигнал, , изменяются больше всего. Если ошибка равна нулю, то весов не должно быть. Если связанное значение X равно нулю, то изменение веса не имеет значения, поэтому оно не изменяется. ${\displaystyle y_{k}}$

Конвергенция

μ контролирует, насколько быстро и насколько хорошо алгоритм сходится к оптимальным коэффициентам фильтра. Если μ слишком велико, алгоритм не будет сходиться. Если μ слишком мало, алгоритм сходится медленно и может не успеть отследить изменяющиеся условия. Если μ велико, но не слишком велико, чтобы предотвратить сходимость, алгоритм быстро достигает устойчивого состояния, но постоянно превышает оптимальный весовой вектор. Иногда μ сначала делают большим для быстрой сходимости, а затем уменьшают, чтобы минимизировать перерегулирование.

В 1985 году Уидроу и Стернс заявили, что им неизвестно доказательство того, что алгоритм LMS будет сходиться во всех случаях. ^[7]

Однако при определенных предположениях о стационарности и независимости можно показать, что алгоритм будет сходиться, если

${\displaystyle 0<\mu <{\frac {1}{\sigma ^{2}}}}$

где

${\displaystyle \sigma ^{2}=\sum _{l=0}^{L}\sigma _{l}^{2}}$= сумма всей входной мощности

${\displaystyle \sigma _{l}}$это среднеквадратичное значение 'го входа ${\displaystyle l}$

В случае фильтра с отводной линией задержки каждый вход имеет одинаковое значение RMS, поскольку они просто являются одинаковыми значениями, задержанными. В этом случае общая мощность равна

${\displaystyle \sigma ^{2}=(L+1)\sigma _{0}^{2}}$

где

${\displaystyle \sigma _{0}}$это среднеквадратичное значение входного потока. ^[7] ${\displaystyle x_{k}}$

Это приводит к нормализованному алгоритму LMS:

${\displaystyle w_{l,k+1}=w_{lk}+\left({\frac {2\mu _{\sigma }}{\sigma ^{2}}}\right)\epsilon _{k}\ x_{k-l}}$в этом случае критерий сходимости становится: . ${\displaystyle 0<\mu _{\sigma }<1}$

Нелинейные адаптивные фильтры

Целью нелинейных фильтров является преодоление ограничений линейных моделей. Существует несколько часто используемых подходов: Volterra LMS, Kernel Adaptive Filter , Spline Adaptive Filter ^[8] и Urysohn Adaptive Filter. ^{[9] [10]} Многие авторы ^[11] также включают в этот список нейронные сети. Общая идея Volterra LMS и Kernel LMS заключается в замене выборок данных различными нелинейными алгебраическими выражениями. Для Volterra LMS этим выражением является ряд Вольтерры . В Spline Adaptive Filter модель представляет собой каскад линейного динамического блока и статической нелинейности, который аппроксимируется сплайнами. В Urysohn Adaptive Filter линейные члены в модели

${\displaystyle y_{i}=\sum _{j=0}^{m}w_{j}\ x_{ij}}$

заменяются кусочно-линейными функциями

${\displaystyle y_{i}=\sum _{j=0}^{m}f_{j}(x_{ij})}$

которые определяются из выборок данных.

Применение адаптивных фильтров

• Адаптивное шумоподавление
• Контроль акустического шума
• Прогнозирование сигнала
• Адаптивное подавление обратной связи
• Эхоподавление

Реализации фильтров

• Фильтр наименьших средних квадратов
• Рекурсивный фильтр наименьших квадратов
• Многоблочный адаптивный фильтр частотной области с несколькими задержками

Смотрите также

• 2D адаптивные фильтры
• Фильтр (обработка сигнала)
• фильтр Калмана
• Адаптивный фильтр ядра
• Линейное предсказание
• оценщик MMSE
• фильтр Винера
• Уравнение Винера–Хопфа

Ссылки

1. Thakor, NV; Zhu, Yi-Sheng (1991-08-01). «Применение адаптивной фильтрации к анализу ЭКГ: шумоподавление и обнаружение аритмии». IEEE Transactions on Biomedical Engineering . 38 (8): 785–794. doi :10.1109/10.83591. ISSN  0018-9294. PMID  1937512. S2CID  11271450.
2. Уидроу, Бернард; Стернс, Сэмюэл Д. (1985). Адаптивная обработка сигналов (1-е изд.). Prentice-Hall. стр. 329. ISBN 978-0130040299.
3. Видроу, стр. 304
4. Видроу, стр. 212
5. Видроу стр. 313
6. Видроу стр. 100
7. Widrow стр. 103
8. Данило Комминиелло; Хосе С. Принсипе (2018). Методы адаптивного обучения для моделирования нелинейных систем . Elsevier Inc. ISBN 978-0-12-812976-0.
9. М.Полуэктов и А.Полярный. Адаптивный фильтр Урысона. 2019.
10. «Нелинейная адаптивная фильтрация». ezcodesample.com .
11. Вэйфэн Лю; Хосе К. Принсипи; Саймон Хайкин (март 2010 г.). Адаптивная фильтрация ядра: подробное введение (PDF) . Уайли. стр. 12–20. ISBN 978-0-470-44753-6.

Источники

• Хейс, Монсон Х. (1996). Статистическая цифровая обработка сигналов и моделирование . Wiley. ISBN 978-0-471-59431-4.
• Хайкин, Саймон (2002). Теория адаптивного фильтра . Prentice Hall. ISBN 978-0-13-048434-5.
• Widrow, Bernard; Stearns, Samuel D. (1985). Адаптивная обработка сигналов . Englewood Cliffs, NJ: Prentice Hall. ISBN 978-0-13-004029-9.