Фокусное расстояние оптической системы является мерой того, насколько сильно система сходится или расходится свет ; это обратная величина оптической силы системы . Положительное фокусное расстояние указывает на то, что система сходится или расходится свет, в то время как отрицательное фокусное расстояние указывает на то, что система расходится свет. Система с меньшим фокусным расстоянием изгибает лучи резче, сводя их в фокус на более коротком расстоянии или расходя их быстрее. Для особого случая тонкой линзы в воздухе положительное фокусное расстояние — это расстояние, на котором изначально коллимированные (параллельные) лучи сводятся в фокус , или, в качестве альтернативы, отрицательное фокусное расстояние указывает, насколько далеко перед линзой должен быть расположен точечный источник , чтобы сформировать коллимированный пучок. Для более общих оптических систем фокусное расстояние не имеет интуитивного смысла; это просто обратная величина оптической силы системы.
В большинстве фотографий и всех телескопах , где объект находится по существу бесконечно далеко, большее фокусное расстояние (меньшая оптическая сила) приводит к большему увеличению и более узкому углу зрения ; и наоборот, меньшее фокусное расстояние или большая оптическая сила связаны с меньшим увеличением и более широким углом зрения. С другой стороны, в таких приложениях, как микроскопия , в которых увеличение достигается путем приближения объекта к объективу, меньшее фокусное расстояние (большая оптическая сила) приводит к большему увеличению, поскольку объект может быть приближен к центру проекции.
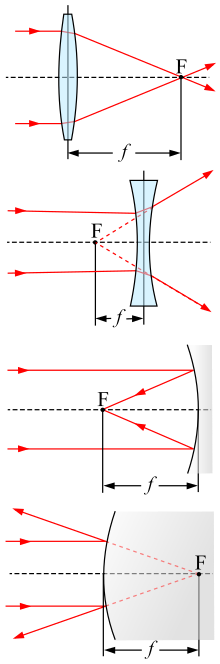
Для тонкой линзы в воздухе фокусное расстояние — это расстояние от центра линзы до главных фокусов (или фокальных точек ) линзы. Для собирающей линзы (например, выпуклой линзы ) фокусное расстояние положительно и представляет собой расстояние, на котором пучок коллимированного света будет сфокусирован в одну точку. Для рассеивающей линзы (например, вогнутой линзы ) фокусное расстояние отрицательно и представляет собой расстояние до точки, из которой коллимированный пучок кажется расходящимся после прохождения через линзу.
Когда линза используется для формирования изображения некоторого объекта, расстояние от объекта до линзы u , расстояние от линзы до изображения v и фокусное расстояние f связаны соотношением
Фокусное расстояние тонкой выпуклой линзы можно легко измерить, используя ее для формирования изображения удаленного источника света на экране. Линза перемещается до тех пор, пока на экране не образуется четкое изображение. В этом случае 1/ты пренебрежимо мало, и фокусное расстояние тогда определяется как
Определение фокусного расстояния вогнутой линзы несколько сложнее. Фокусное расстояние такой линзы определяется как точка, в которой встречаются распространяющиеся лучи света, когда они вытянуты назад. Во время такого теста изображение не формируется, и фокусное расстояние должно быть определено путем пропускания света (например, света лазерного луча) через линзу, изучения того, насколько этот свет рассеивается/преломляется, и отслеживания луча света назад к фокусной точке линзы.

Для толстой линзы (имеющей существенную толщину) или системы формирования изображения, состоящей из нескольких линз или зеркал (например, фотографического объектива или телескопа ), существует несколько связанных понятий, которые называются фокусными расстояниями:
Для оптической системы в воздухе эффективное фокусное расстояние, переднее фокусное расстояние и заднее фокусное расстояние одинаковы и могут быть названы просто «фокусным расстоянием».

Для оптической системы в среде, отличной от воздуха или вакуума, переднее и заднее фокусные расстояния равны EFL, умноженному на показатель преломления среды перед линзой или за ней ( n 1 и n 2 на схеме выше). Термин «фокусное расстояние» сам по себе неоднозначен в этом случае. Исторически «фокусное расстояние» определялось как EFL, умноженное на показатель преломления среды. [2] [4] Для системы с различными средами с обеих сторон, такой как человеческий глаз, переднее и заднее фокусные расстояния не равны друг другу, и соглашение может диктовать, какое из них называть «фокусным расстоянием» системы. Некоторые современные авторы избегают этой неоднозначности, вместо этого определяя «фокусное расстояние» как синоним EFL. [1]
Различие между передним/задним фокусным расстоянием и EFL важно для изучения человеческого глаза. Глаз может быть представлен эквивалентной тонкой линзой на границе воздух/жидкость с передним и задним фокусным расстоянием, равным таковым глаза, или он может быть представлен другой эквивалентной тонкой линзой, которая полностью находится в воздухе, с фокусным расстоянием, равным EFL глаза.
Для случая линзы толщиной d в воздухе ( n 1 = n 2 = 1 ) и поверхностей с радиусами кривизны R 1 и R 2 эффективное фокусное расстояние f определяется уравнением Линзмейкера : [5]
где n — показатель преломления линзовой среды. Величина 1/ф также известна как оптическая сила линзы.
Соответствующее переднее фокусное расстояние равно: [6] а заднее фокусное расстояние:
В используемом здесь соглашении о знаках значение R 1 будет положительным, если первая поверхность линзы выпуклая, и отрицательным, если она вогнутая. Значение R 2 будет отрицательным, если вторая поверхность выпуклая, и положительным, если вогнутая. Соглашения о знаках различаются у разных авторов, что приводит к разным формам этих уравнений в зависимости от используемого соглашения.
Для сферически изогнутого зеркала в воздухе величина фокусного расстояния равна радиусу кривизны зеркала, делённому на два. Фокусное расстояние положительно для вогнутого зеркала и отрицательно для выпуклого зеркала. В соглашении о знаках, используемом в оптическом проектировании, вогнутое зеркало имеет отрицательный радиус кривизны, поэтому
где R — радиус кривизны поверхности зеркала.
Дополнительную информацию о правиле знаков для радиуса кривизны, используемом здесь, см. в разделе Радиус кривизны (оптика).


Фокусное расстояние объектива камеры обычно указывается в миллиметрах (мм), но некоторые старые объективы имеют маркировку в сантиметрах (см) или дюймах.
Фокусное расстояние ( f ) и поле зрения (FOV) объектива обратно пропорциональны. Для стандартной прямолинейной линзы , , где x — ширина пленки или датчика изображения.
Когда фотографический объектив установлен на «бесконечность», его задняя главная плоскость отделена от сенсора или пленки, которые затем расположены в фокальной плоскости , фокусным расстоянием объектива. Объекты, удаленные от камеры, затем создают резкие изображения на сенсоре или пленке, которые также находятся в плоскости изображения.
Чтобы сделать более близкие объекты резкими, объектив необходимо отрегулировать так, чтобы увеличить расстояние между задней главной плоскостью и пленкой, чтобы поместить пленку в плоскость изображения. Фокусное расстояние f , расстояние от передней главной плоскости до объекта для фотографирования s 1 и расстояние от задней главной плоскости до плоскости изображения s 2 затем связаны соотношением:
При уменьшении s 1 необходимо увеличить s 2. Например, рассмотрим обычный объектив для 35-мм камеры с фокусным расстоянием f = 50 мм. Для фокусировки удаленного объекта ( s 1 ≈ ∞ ) задняя главная плоскость объектива должна быть расположена на расстоянии s 2 = 50 мм от плоскости пленки, так чтобы она находилась в месте расположения плоскости изображения. Для фокусировки объекта на расстоянии 1 м ( s 1 = 1000 мм) объектив необходимо переместить на 2,6 мм дальше от плоскости пленки, до s 2 = 52,6 мм.
Фокусное расстояние объектива определяет увеличение, при котором он отображает удаленные объекты. Оно равно расстоянию между плоскостью изображения и отверстием, которое отображает удаленные объекты того же размера, что и рассматриваемый объектив. Для прямолинейных линз (то есть без искажения изображения ) отображение удаленных объектов хорошо моделируется как модель камеры-обскуры . [7] Эта модель приводит к простой геометрической модели, которую фотографы используют для вычисления угла зрения камеры; в этом случае угол зрения зависит только от отношения фокусного расстояния к размеру пленки . В общем случае угол зрения зависит также от искажения. [8]
Объектив с фокусным расстоянием, примерно равным диагонали формата пленки или сенсора, называется нормальным объективом ; его угол обзора аналогичен углу, образуемому достаточно большим отпечатком, просматриваемым с типичного расстояния просмотра диагонали отпечатка, что, следовательно, дает нормальную перспективу при просмотре отпечатка; [9] этот угол обзора составляет около 53 градусов по диагонали. Для полнокадровых камер формата 35 мм диагональ составляет 43 мм, а типичный «нормальный» объектив имеет фокусное расстояние 50 мм. Объектив с фокусным расстоянием короче нормального часто называют широкоугольным объективом (обычно 35 мм и меньше для камер формата 35 мм), в то время как объектив значительно длиннее нормального может называться телеобъективом ( обычно 85 мм и больше для камер формата 35 мм). Технически длиннофокусные объективы являются «телеобъективами», только если фокусное расстояние больше физической длины объектива, но этот термин часто используется для описания любого длиннофокусного объектива.
Из-за популярности стандарта 35 мм комбинации камера-объектив часто описываются в терминах их 35-мм эквивалентного фокусного расстояния, то есть фокусного расстояния объектива, который имел бы тот же угол обзора или поле зрения, если бы использовался на полнокадровой 35-мм камере. Использование 35-мм эквивалентного фокусного расстояния особенно распространено в цифровых камерах , которые часто используют датчики меньше, чем 35-мм пленка, и поэтому требуют соответственно более коротких фокусных расстояний для достижения заданного угла обзора, по фактору, известному как кроп-фактор .

Оптическая сила линзы или изогнутого зеркала — это физическая величина , равная обратной величине фокусного расстояния, выраженная в метрах . Диоптрия — это единица измерения с размерностью обратной длины , эквивалентной одному обратному метру , 1 диоптрия = 1 м − 1 . Например, линза в 2 диоптрии фокусирует параллельные лучи света на расстоянии 1 ⁄ 2 метра. Плоское окно имеет оптическую силу в ноль диоптрий, поскольку оно не заставляет свет сходиться или расходиться. [10]
Главное преимущество использования оптической силы вместо фокусного расстояния заключается в том, что формула тонкой линзы имеет расстояние до объекта, расстояние до изображения и фокусное расстояние как обратные величины. Кроме того, когда относительно тонкие линзы располагаются близко друг к другу, их силы приблизительно складываются. Таким образом, тонкая линза в 2,0 диоптрии, расположенная близко к тонкой линзе в 0,5 диоптрии, дает почти такое же фокусное расстояние, как и одна линза в 2,5 диоптрии.