Дициклическая группа

В теории групп дициклическая группа ( обозначение Dic _n или Q _{4 n} , ^[1] ⟨ n ,2,2⟩ ^[2] ) — это особый вид неабелевой группы порядка 4 n ( n > 1). Это расширение циклической группы порядка 2 циклической группой порядка 2 n , что дает название дициклическая . В обозначениях точных последовательностей групп это расширение можно выразить как:

${\displaystyle 1\to C_{2n}\to {\mbox{Dic}}_{n}\to C_{2}\to 1.\,}$

В более общем случае для любой конечной абелевой группы с элементом порядка 2 можно определить дициклическую группу.

Определение

Для каждого целого числа n > 1 дициклическая группа Dic _n может быть определена как подгруппа единичных кватернионов, порожденных

${\displaystyle {\begin{aligned}a&=e^{\frac {i\pi }{n}}=\cos {\frac {\pi }{n}}+i\sin {\frac {\pi }{n}}\\x&=j\end{aligned}}}$

Более абстрактно можно определить дициклическую группу Dic _n как группу со следующим представлением ^[3]

${\displaystyle \operatorname {Dic} _{n}=\left\langle a,x\mid a^{2n}=1,\ x^{2}=a^{n},\ x^{-1}ax=a^{-1}\right\rangle .\,\!}$

Из этого определения следует несколько важных моментов:

• ${\displaystyle x^{4}=1}$
• ${\displaystyle x^{2}a^{m}=a^{m+n}=a^{m}x^{2}}$
• если , то ${\displaystyle l=\pm 1}$ ${\displaystyle x^{l}a^{m}=a^{-m}x^{l}}$
• ${\displaystyle a^{m}x^{-1}=a^{m-n}a^{n}x^{-1}=a^{m-n}x^{2}x^{-1}=a^{m-n}x}$

Таким образом, каждый элемент Dic _n может быть однозначно записан как a ^m x ^l , где 0 ≤ m < 2 n и l = 0 или 1. Правила умножения задаются как

• ${\displaystyle a^{k}a^{m}=a^{k+m}}$
• ${\displaystyle a^{k}a^{m}x=a^{k+m}x}$
• ${\displaystyle a^{k}xa^{m}=a^{k-m}x}$
• ${\displaystyle a^{k}xa^{m}x=a^{k-m+n}}$

Отсюда следует, что Dic _n имеет порядок 4 n . ^[3]

Когда n = 2, дициклическая группа изоморфна группе кватернионов Q. В более общем случае, когда n является степенью 2, дициклическая группа изоморфна обобщенной группе кватернионов . ^[3]

Характеристики

Для каждого n > 1 дициклическая группа Dic _n является неабелевой группой порядка 4 n . (Для вырожденного случая n = 1 группа Dic ₁ является циклической группой C ₄ , которая не считается дициклической.)

Пусть A = ⟨ a ⟩ — подгруппа Dic _{n ,} порождённая a . Тогда A — циклическая группа порядка 2 n , поэтому [Dic _n : A ] = 2. Как подгруппа индекса 2 она автоматически является нормальной подгруппой . Фактор-группа Dic _n / A — циклическая группа порядка 2.

Dic _n разрешим ; заметим, что A является нормальным и, будучи абелевым, сам по себе разрешим.

Бинарная диэдральная группа

Дициклическая группа является бинарным полиэдральным коллективом — это один из классов подгрупп группы Pin Pin ₋ (2), которая является подгруппой группы Spin Spin(3) — и в этом контексте известна как бинарная диэдральная группа .

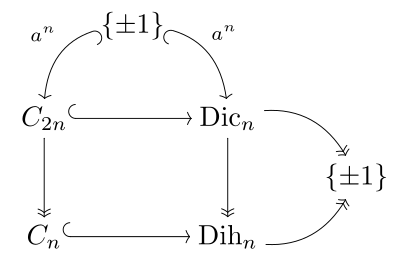
Связь с бинарной циклической группой C _{2 n} , циклической группой C _n и диэдральной группой Dih _n порядка 2 n проиллюстрирована на диаграмме справа и параллельна соответствующей диаграмме для группы Pin. Коксетер записывает бинарную диэдральную группу как ⟨2,2, n ⟩ и бинарную циклическую группу с угловыми скобками, ⟨ n ⟩.

Существует поверхностное сходство между дициклическими группами и диэдральными группами ; обе являются своего рода «зеркальным отражением» базовой циклической группы. Но представление диэдральной группы имело бы x ² = 1 вместо x ² = a ⁿ ; и это дает другую структуру. В частности, Dic _n не является полупрямым произведением A и ⟨ x ⟩ , поскольку A  ∩  ⟨ x ⟩ не является тривиальным.

Дициклическая группа имеет единственную инволюцию (т.е. элемент порядка 2), а именно x ² = a ⁿ . Обратите внимание, что этот элемент лежит в центре Dic _n . Действительно, центр состоит исключительно из единичного элемента и x ² . Если мы добавим отношение x ² = 1 к представлению Dic _{n ,} то получим представление диэдральной группы Dih _n , поэтому фактор-группа Dic _n /< x ² > изоморфна Dih _n .

Существует естественный гомоморфизм 2-к-1 из группы единичных кватернионов в 3-мерную группу вращений, описанную в кватернионах и пространственных вращениях . Поскольку дициклическая группа может быть вложена внутрь единичных кватернионов, можно спросить, каков ее образ при этом гомоморфизме. Ответом является просто группа диэдральной симметрии Dih _n . По этой причине дициклическая группа также известна как бинарная диэдральная группа . Обратите внимание, что дициклическая группа не содержит подгрупп, изоморфных Dih _n .

Аналогичная конструкция прообраза, использующая Pin ₊ (2) вместо Pin ₋ (2), дает другую диэдральную группу, Dih _{2 n} , а не дициклическую группу.

Обобщения

Пусть A — абелева группа , имеющая определенный элемент y в A с порядком 2. Группа G называется обобщенной дициклической группой , записываемой как Dic( A , y ) , если она порождается A и дополнительным элементом x , и, кроме того, мы имеем, что [ G : A ] = 2, x ² = y , и для всех a из A , x ⁻¹ ax = a ⁻¹ .

Поскольку для циклической группы четного порядка всегда существует единственный элемент порядка 2, мы видим, что дициклические группы представляют собой всего лишь частный тип обобщенной дициклической группы.

Дициклическая группа является случаем семейства бинарных треугольных групп, определяемых представлением:[1] ${\displaystyle (p,q,r)=(2,2,n)}$ ${\displaystyle \Gamma (p,q,r)}$

${\displaystyle \langle a,b,c\mid a^{p}=b^{q}=c^{r}=abc\rangle .}$

Факторизация по дополнительному отношению дает обычную треугольную группу , которая в данном случае является диэдральным фактором . ${\displaystyle abc=e}$ ${\displaystyle \mathrm {Dic} _{n}\rightarrow \mathrm {Dih} _{n}}$

Смотрите также

• бинарная полиэдральная группа
• бинарная циклическая группа , ⟨ n ⟩, порядок 2 n
• бинарная тетраэдрическая группа , 2T = ⟨2,3,3⟩, ^[2] порядок 24
• бинарная октаэдрическая группа , 2O = ⟨2,3,4⟩, ^[2] порядок 48
• бинарная икосаэдрическая группа , 2I = ⟨2,3,5⟩, ^[2] порядок 120

Ссылки

1. Николсон, В. Кит (1999). Введение в абстрактную алгебру (2-е изд.). Нью-Йорк: John Wiley & Sons, Inc. стр. 449. ISBN 0-471-33109-0.
2. Коксетер и Мозер: Генераторы и соотношения для дискретных групп: <l,m,n>: R ^l = S ^m = T ⁿ = RST
3. Роман, Стивен (2011). Основы теории групп: продвинутый подход . Springer. стр. 347–348. ISBN 9780817683016.

• Коксетер, HSM (1974), «7.1 Циклические и дициклические группы», Регулярные комплексные многогранники , Cambridge University Press, стр. 74–75.
• Coxeter, HSM; Moser, WOJ (1980). Генераторы и отношения для дискретных групп . Нью-Йорк: Springer-Verlag. ISBN 0-387-09212-9.

Внешние ссылки

• Дициклические группы на GroupNames