В ядерной физике , атомной физике и ядерной химии оболочечная модель ядра использует принцип исключения Паули для моделирования структуры атомных ядер с точки зрения энергетических уровней. [1] Первая оболочечная модель была предложена Дмитрием Иваненко (совместно с Э. Гапоном) в 1932 году. Модель была разработана в 1949 году в результате независимой работы нескольких физиков, в первую очередь Марии Гёпперт Майер и Й. Ганса Д. Йенсена , которые получили Нобелевскую премию по физике в 1963 году за свой вклад в эту модель, и Юджина Вигнера , который получил Нобелевскую премию вместе с ними за свою более раннюю основополагающую работу по атомным ядрам. [2]
Модель ядерной оболочки частично аналогична модели атомной оболочки , которая описывает расположение электронов в атоме, в том смысле, что заполненная оболочка приводит к лучшей стабильности. При добавлении нуклонов ( протонов и нейтронов ) к ядру существуют определенные точки, в которых энергия связи следующего нуклона значительно меньше, чем у последнего. Это наблюдение, что существуют определенные магические квантовые числа нуклонов ( 2, 8, 20, 28, 50, 82 и 126 ), которые связаны более прочно, чем следующее большее число, является источником модели оболочки.
Оболочки для протонов и нейтронов независимы друг от друга. Поэтому могут существовать как «магические ядра», в которых один или другой тип нуклона находится под магическим числом, так и « дважды магические квантовые ядра », где оба находятся под магическим числом. Из-за вариаций в заполнении орбит верхние магические числа составляют 126 и, предположительно, 184 для нейтронов, но только 114 для протонов, что играет роль в поиске так называемого острова стабильности . Были найдены некоторые полумагические числа, в частности Z = 40 , которое дает заполнение ядерной оболочки для различных элементов; 16 также может быть магическим числом. [3]
Чтобы получить эти числа, модель ядерной оболочки начинается со среднего потенциала с формой где-то между квадратной ямой и гармоническим осциллятором . К этому потенциалу добавляется член спин-орбиты. Тем не менее, полное возмущение не совпадает с экспериментом, и необходимо добавить эмпирическую спин-орбитальную связь с по крайней мере двумя или тремя различными значениями ее константы связи в зависимости от изучаемых ядер.
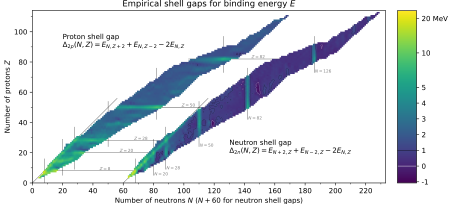
Магические числа ядер, а также другие свойства, могут быть получены путем аппроксимации модели трехмерным гармоническим осциллятором плюс спин-орбитальное взаимодействие . Более реалистичный, но сложный потенциал известен как потенциал Вудса-Саксона .
Рассмотрим трехмерный гармонический осциллятор . Это дало бы, например, на первых трех уровнях (" ℓ " - квантовое число углового момента ):
Ядра строятся путем добавления протонов и нейтронов . Они всегда будут заполнять самый нижний доступный уровень, причем первые два протона заполняют нулевой уровень, следующие шесть протонов заполняют уровень один и так далее. Как и в случае с электронами в периодической таблице , протоны в самой внешней оболочке будут относительно слабо связаны с ядром, если в этой оболочке всего несколько протонов, поскольку они находятся дальше всего от центра ядра. Поэтому ядра с полной внешней протонной оболочкой будут иметь более высокую энергию ядерной связи , чем другие ядра с аналогичным общим числом протонов. То же самое верно и для нейтронов.
Это означает, что магическими числами, как ожидается, будут те, в которых все занятые оболочки заполнены. В соответствии с экспериментом, мы получаем 2 (уровень 0 заполнен) и 8 (уровни 0 и 1 заполнены) для первых двух чисел. Однако полный набор магических чисел получается некорректным. Их можно вычислить следующим образом:
В частности, первые шесть снарядов:
где для каждого ℓ существует 2 ℓ +1 различных значений m l и 2 значения m s , что дает в общей сложности 4 ℓ +2 состояния для каждого конкретного уровня.
Эти числа в два раза превышают значения треугольных чисел из треугольника Паскаля: 1, 3, 6, 10, 15, 21, ....
Далее мы включаем спин-орбитальное взаимодействие . Во -первых, мы должны описать систему квантовыми числами j, mj и четностью вместо ℓ, ml и ms , как в водородоподобном атоме . Поскольку каждый четный уровень включает только четные значения ℓ , он включает только состояния четной (положительной) четности. Аналогично, каждый нечетный уровень включает только состояния нечетной (отрицательной) четности. Таким образом, мы можем игнорировать четность при подсчете состояний. Первые шесть оболочек, описываемые новыми квантовыми числами, следующие:
где для каждого j существует 2 j + 1 различных состояний из различных значений m j .
Из-за спин-орбитального взаимодействия энергии состояний одного и того же уровня, но с разными j больше не будут идентичны. Это происходит потому, что в исходных квантовых числах, когда параллельно , энергия взаимодействия положительна, и в этом случае j = ℓ + s = ℓ + 1/2 . Когда антипараллелен (т.е. выровнен противоположно), энергия взаимодействия отрицательна, и в этом случае j = ℓ − s = ℓ − 1/2 . Более того, сила взаимодействия примерно пропорциональнаℓ.
Например, рассмотрим состояния на уровне 4:
Потенциал гармонического осциллятора бесконечно растет по мере того, как расстояние от центра r стремится к бесконечности. Более реалистичный потенциал, такой как потенциал Вудса–Саксона , приближался бы к константе на этом пределе. Одним из главных следствий является то, что средний радиус орбит нуклонов был бы больше в реалистичном потенциале. Это приводит к уменьшению члена в операторе Лапласа оператора Гамильтона . Другое главное отличие состоит в том, что орбиты с высокими средними радиусами, такие как с высоким n или высоким ℓ , будут иметь более низкую энергию, чем в потенциале гармонического осциллятора. Оба эффекта приводят к снижению уровней энергии орбит с высоким ℓ .

Вместе со спин-орбитальным взаимодействием и при соответствующих величинах обоих эффектов получается следующая качественная картина: на всех уровнях самые высокие j- состояния смещаются вниз по энергии, особенно при высоких n (где самое высокое j -состояния высокие). Это происходит как из-за отрицательной энергии спин-орбитального взаимодействия, так и из-за уменьшения энергии в результате деформации потенциала в более реалистичный. Вторые по величине j- состояния, напротив, смещаются вверх из-за первого эффекта и вниз из-за второго эффекта, что приводит к небольшому общему сдвигу. Сдвиги энергии самых высоких j -состояний могут, таким образом, приблизить энергию состояний одного уровня к энергии состояний более низкого уровня. Тогда «оболочки» оболочечной модели больше не идентичны уровням, обозначенным n , и магические числа изменяются.
Затем мы можем предположить, что наивысшие j -состояния для n = 3 имеют промежуточную энергию между средними энергиями n = 2 и n = 3, и предположить, что наивысшие j -состояния для больших n (по крайней мере до n = 7) имеют энергию, близкую к средней энергии n − 1. Тогда мы получаем следующие оболочки (см. рисунок)
и так далее.
Обратите внимание, что числа состояний после 4-й оболочки представляют собой удвоенные треугольные числа плюс два . Спин-орбитальная связь заставляет так называемые «уровни нарушителей» опускаться со следующей более высокой оболочки в структуру предыдущей оболочки. Размеры нарушителей таковы, что результирующие размеры оболочек сами увеличиваются до следующих более высоких удвоенных треугольных чисел от размеров гармонического осциллятора. Например, 1f2p имеет 20 нуклонов, а спин-орбитальная связь добавляет 1g9/2 (10 нуклонов), что приводит к новой оболочке с 30 нуклонами. 1g2d3s имеет 30 нуклонов, а добавление нарушителя 1h11/2 (12 нуклонов) дает новый размер оболочки 42 и т. д.
Тогда магические числа будут такими:
и т. д. Это дает все наблюдаемые магические числа, а также предсказывает новое (так называемый остров стабильности ) со значением 184 (для протонов магическое число 126 пока не наблюдалось, и более сложные теоретические соображения предсказывают, что магическое число будет равно 114).
Другой способ предсказать магические (и полумагические) числа — это выложить идеализированный порядок заполнения (с расщеплением спин-орбиты, но без перекрытия энергетических уровней). Для согласованности s делится на j = 1/2 и j = − 1/2 компоненты с 2 и 0 членами соответственно. Взятие самого левого и самого правого общих чисел в последовательностях, ограниченных /, здесь дает магические и полумагические числа.
Самые правые предсказанные магические числа каждой пары в пределах квартетов, разделенных пополам /, являются двойными тетраэдрическими числами из треугольника Паскаля: 2, 8, 20, 40, 70, 112, 168, 240 равны 2x 1, 4, 10, 20, 35, 56, 84, 120, ..., а самые левые члены пар отличаются от самых правых двойными треугольными числами: 2 − 2 = 0, 8 − 6 = 2, 20 − 14 = 6, 40 − 28 = 12, 70 − 50 = 20, 112 − 82 = 30, 168 − 126 = 42, 240 − 184 = 56, где 0, 2, 6, 12, 20, 30, 42, 56, ... — это 2 × 0, 1, 3, 6, 10, 15, 21, 28, ... .
Эта модель также предсказывает или объясняет с некоторым успехом другие свойства ядер, в частности спин и четность основных состояний ядер , а также в некоторой степени их возбужденные ядерные состояния . Возьмите17
8Например, O ( кислород-17 ): его ядро имеет восемь протонов, заполняющих первые три протонные «оболочки», восемь нейтронов, заполняющих первые три нейтронные «оболочки», и один дополнительный нейтрон. Все протоны в полной протонной оболочке имеют нулевой полный угловой момент , поскольку их угловые моменты компенсируют друг друга. То же самое верно и для нейтронов. Все протоны на одном уровне ( n ) имеют одинаковую четность (либо +1, либо −1), и поскольку четность пары частиц является произведением их четностей, четное число протонов с одного уровня ( n ) будет иметь четность +1. Таким образом, полный угловой момент восьми протонов и первых восьми нейтронов равен нулю, а их общая четность равна +1. Это означает, что спин (т. е. угловой момент) ядра, а также его четность полностью определяются четностью девятого нейтрона. Этот находится в первом (т.е. с самой низкой энергией) состоянии 4-й оболочки, которая является d-оболочкой ( ℓ = 2), и поскольку p = (−1) ℓ , это дает ядру общую четность +1. Эта 4-я d-оболочка имеет j = 5/2 , таким образом, ядро17
8Ожидается, что O имеет положительную четность и полный угловой момент 5/2 , что действительно так и есть.
Правила упорядочения ядерных оболочек аналогичны правилам Хунда для атомных оболочек, однако, в отличие от их использования в атомной физике, завершение оболочки не означает достижение следующего n , поэтому оболочечная модель не может точно предсказать порядок возбужденных состояний ядер, хотя она очень успешна в предсказании основных состояний. Порядок первых нескольких членов перечислен следующим образом: 1s, 1p 3/2 , 1п 1/2 , 1д 5/2 , 2с, 1д 3/2 ... Для получения дополнительных разъяснений по обозначениям обратитесь к статье о символе термина Рассела–Сондерса .
Для ядер, более далеких от магических квантовых чисел, необходимо добавить предположение, что из-за связи между сильным ядерным взаимодействием и полным угловым моментом протоны или нейтроны с одинаковым n имеют тенденцию образовывать пары с противоположным угловым моментом. Поэтому ядро с четным числом протонов и четным числом нейтронов имеет 0 спина и положительную четность. Ядро с четным числом протонов и нечетным числом нейтронов (или наоборот) имеет четность последнего нейтрона (или протона), а спин равен полному угловому моменту этого нейтрона (или протона). Под «последним» мы подразумеваем свойства, исходящие из самого высокого энергетического уровня.
В случае ядра с нечетным числом протонов и нечетным числом нейтронов необходимо учитывать полный угловой момент и четность как последнего нейтрона, так и последнего протона. Четность ядра будет их произведением, тогда как спин ядра будет одним из возможных результатов суммы их угловых моментов (другими возможными результатами будут возбужденные состояния ядра).
Упорядочение уровней углового момента внутри каждой оболочки происходит в соответствии с принципами, описанными выше, – из-за спин-орбитального взаимодействия, при этом состояния с высоким угловым моментом имеют смещенную вниз энергию из-за деформации потенциала (т.е. перехода от потенциала гармонического осциллятора к более реалистичному). Однако для пар нуклонов часто энергетически выгодно находиться при высоком угловом моменте, даже если его уровень энергии для одного нуклона был бы выше. Это связано с соотношением между угловым моментом и сильным ядерным взаимодействием .
Ядерный магнитный момент нейтронов и протонов частично предсказывается этой простой версией оболочечной модели. Магнитный момент вычисляется через j , ℓ и s "последнего" нуклона, но ядра не находятся в состояниях четко определенных ℓ и s . Кроме того, для нечетно-нечетных ядер необходимо рассмотреть два "последних" нуклона, как в дейтерии . Таким образом, мы получаем несколько возможных ответов для ядерного магнитного момента, по одному для каждого возможного комбинированного состояния ℓ и s , и реальное состояние ядра является их суперпозицией . Таким образом, реальный (измеренный) ядерный магнитный момент находится где-то между возможными ответами.
Электрический диполь ядра всегда равен нулю, поскольку его основное состояние имеет определенную четность. Плотность материи ( ψ 2 , где ψ — волновая функция ) всегда инвариантна относительно четности. Обычно это касается атомного электрического диполя .
Более высокие электрические и магнитные мультипольные моменты не могут быть предсказаны этой простой версией оболочечной модели по причинам, аналогичным тем, что существуют в случае дейтерия .

Для ядер, имеющих два или более валентных нуклона (т.е. нуклонов вне замкнутой оболочки), необходимо добавить остаточное двухчастичное взаимодействие. Этот остаточный член происходит от части межнуклонного взаимодействия, не включенной в аппроксимативный средний потенциал. Благодаря этому включению различные конфигурации оболочек смешиваются, и энергетическое вырождение состояний, соответствующих одной и той же конфигурации, нарушается. [5] [6]
Эти остаточные взаимодействия включаются посредством расчетов модели оболочки в усеченном модельном пространстве (или валентном пространстве). Это пространство охватывается базисом многочастичных состояний, где активны только одночастичные состояния в модельном пространстве. Уравнение Шредингера решается на этой основе с использованием эффективного гамильтониана, специально подходящего для модельного пространства. Этот гамильтониан отличается от гамильтониана свободных нуклонов, поскольку, помимо прочего, он должен компенсировать исключенные конфигурации. [6]
Можно полностью отказаться от приближения среднего потенциала, расширив модельное пространство до ранее инертного ядра и рассматривая все одночастичные состояния вплоть до усечения модельного пространства как активные. Это формирует основу модели оболочки без ядра , которая является методом ab initio . Необходимо включить трехчастичное взаимодействие в такие расчеты, чтобы достичь согласия с экспериментами. [7]
В 1953 году были обнаружены первые экспериментальные примеры вращательных полос в ядрах, причем их энергетические уровни следовали той же схеме энергий J(J+1), что и во вращающихся молекулах. С точки зрения квантовой механики невозможно иметь коллективное вращение сферы, поэтому это означало, что форма этих ядер была несферической. В принципе, эти вращательные состояния можно было бы описать как когерентные суперпозиции возбуждений частица-дырка в базисе, состоящем из одночастичных состояний сферического потенциала. Но в действительности описание этих состояний таким образом является неразрешимым из-за большого количества валентных частиц — и эта неразрешимость была еще больше в 1950-х годах, когда вычислительная мощность была крайне примитивной. По этим причинам Оге Бор , Бен Моттельсон и Свен Йёста Нильссон построили модели, в которых потенциал был деформирован в эллипсоидальную форму. Первая успешная модель этого типа теперь известна как модель Нильссона . По сути, это модель гармонического осциллятора, описанная в этой статье, но с добавленной анизотропией, поэтому частоты осциллятора вдоль трех декартовых осей не все одинаковы. Обычно форма представляет собой вытянутый эллипсоид с осью симметрии, взятой за z. Поскольку потенциал не является сферически симметричным, одночастичные состояния не являются состояниями с хорошим угловым моментом J. Однако к гамильтониану можно добавить множитель Лагранжа , известный как «проворачивающий» член. Обычно вектор угловой частоты ω принимается перпендикулярным оси симметрии, хотя проворачивание наклонной оси также можно рассмотреть. Заполнение одночастичных состояний до уровня Ферми дает состояния, ожидаемый угловой момент вдоль оси проворачивания которых является желаемым значением.
Игал Талми разработал метод получения информации из экспериментальных данных и использования ее для расчета и прогнозирования энергий, которые не были измерены. Этот метод успешно использовался многими физиками-ядерщиками и привел к более глубокому пониманию структуры ядра. Была разработана теория, которая дает хорошее описание этих свойств. Это описание оказалось основой оболочечной модели элегантной и успешной модели взаимодействующих бозонов .
Модель, полученная из модели ядерных оболочек, — это модель альфа-частиц, разработанная Генри Маргенау , Эдвардом Теллером , Дж. К. Перингом, Т. Х. Скирмом , также иногда называемая моделью Скирма . [8] [9] Однако следует отметить, что модель Скирма обычно рассматривается как модель самого нуклона как «облака» мезонов (пионов), а не как модель ядра как «облака» альфа-частиц.