
В геометрии два или более объектов называются концентрическими , если они имеют один и тот же центр . Любая пара (возможно, непохожих) объектов с четко определенными центрами может быть концентрической, включая окружности , сферы , правильные многоугольники , правильные многогранники , параллелограммы, конусы, конические сечения и квадрики. [1]
Геометрические объекты являются коаксиальными , если они имеют одну и ту же ось (линию симметрии). Геометрические объекты с четко определенной осью включают окружности (любую линию, проходящую через центр), сферы, цилиндры , [2] конические сечения и поверхности вращения.
Концентрические объекты часто являются частью широкой категории завитковых узоров , которая также включает спирали (кривая, исходящая из точки и удаляющаяся по мере вращения вокруг нее).
В евклидовой плоскости две окружности, которые являются концентрическими, обязательно имеют разные радиусы друг от друга. [3] Однако окружности в трехмерном пространстве могут быть концентрическими и иметь одинаковый радиус друг от друга, но тем не менее быть разными окружностями. Например, два разных меридиана земного шара концентричны друг другу и земному шару (приблизительно как сфера). В более общем смысле, каждые две большие окружности на сфере концентричны друг другу и сфере. [4]
По теореме Эйлера в геометрии о расстоянии между центром описанной окружности и центром вписанной окружности треугольника, две концентрические окружности (расстояние между которыми равно нулю) являются описанной и вписанной окружностями треугольника тогда и только тогда, когда радиус одной из них вдвое больше радиуса другой, и в этом случае треугольник является равносторонним . [5] : стр. 198
Описанная и вписанная окружности правильного n -угольника , а также сам правильный n -угольник являются концентрическими. Для отношения радиуса описанной окружности к радиусу вписанной окружности для различных n , см. Бицентрический многоугольник#Правильные многоугольники . То же самое можно сказать о вписанной сфере , средней сфере и описанной сфере правильного многогранника .
Область плоскости между двумя концентрическими окружностями представляет собой кольцо , и аналогично область пространства между двумя концентрическими сферами представляет собой сферическую оболочку . [6]
Для данной точки c на плоскости множество всех окружностей, имеющих c в качестве своего центра, образует пучок окружностей . Каждые две окружности в пучке концентричны и имеют разные радиусы. Каждая точка на плоскости, за исключением общего центра, принадлежит ровно одной из окружностей в пучке. Каждые две непересекающиеся окружности и каждый гиперболический пучок окружностей могут быть преобразованы в множество концентрических окружностей с помощью преобразования Мёбиуса . [7] [8]
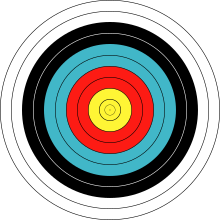
Рябь , образующаяся при падении небольшого предмета в стоячую воду, естественным образом образует расширяющуюся систему концентрических кругов. [9] Равномерно расположенные круги на мишенях, используемых в стрельбе из лука по мишеням [10] или в подобных видах спорта, представляют собой еще один знакомый пример концентрических кругов.
Коаксиальный кабель — это тип электрического кабеля, в котором объединенная нейтральная и заземляющая жила полностью окружает токоведущую жилу(ы) в системе концентрических цилиндрических оболочек. [11]
В «Mysterium Cosmographicum» Иоганна Кеплера была представлена космологическая система, образованная концентрическими правильными многогранниками и сферами. [12]
Концентрические круги использовались на поверхностях огнестрельного оружия в качестве средства удержания смазки или уменьшения трения в компонентах, подобно ювелирным изделиям . [13]
Концентрические круги также встречаются в диоптрических прицелах , типе механических прицелов, обычно используемых на целевых винтовках. Обычно они имеют большой диск с отверстием небольшого диаметра около глаза стрелка и передний шаровой прицел (круг, заключенный внутри другого круга, называемого туннелем ). Если эти прицелы правильно выровнены, точка попадания будет находиться в середине круга переднего прицела.
Сферы: Апостол (2013)
Правильные многоугольники: Харди, Годфри Гарольд (1908), Курс чистой математики, The University Press, стр. 107
Правильные многогранники: Гиллард, Роберт Д. (1987), Комплексная координационная химия: теория и предпосылки, Pergamon Press, стр. 137, 139, ISBN 9780080262321.