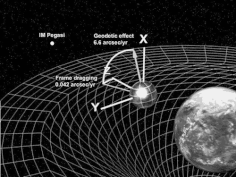
Геодезический эффект

Прецессия спутниковых орбит из-за присутствия небесного тела, влияющего на пространство-время

Представление геодезического эффекта со значениями для гравитационного зонда B.

Геодезический эффект (также известный как геодезическая прецессия , прецессия де Ситтера или эффект де Ситтера ) представляет собой эффект кривизны пространства-времени , предсказанный общей теорией относительности , на вектор, переносимый вместе с вращающимся телом. Например, вектор может быть угловым моментом гироскопа, вращающегося вокруг Земли, как это было выполнено в эксперименте Gravity Probe B. Геодезический эффект был впервые предсказан Виллемом де Ситтером в 1916 году, который предоставил релятивистские поправки к движению системы Земля-Луна. Работа де Ситтера была расширена в 1918 году Яном Схоутеном и в 1920 году Адрианом Фоккером . ^[1] Его также можно применить к конкретной вековой прецессии астрономических орбит, эквивалентной вращению вектора Лапласа-Рунге-Ленца . ^[2]

Термин геодезический эффект имеет два немного разных значения, поскольку движущееся тело может быть вращающимся или невращающимся. Невращающиеся тела движутся по геодезическим , тогда как вращающиеся тела движутся по немного другим орбитам. ^[3]

Разница между прецессией де Ситтера и прецессией Лензе–Тирринга (перетаскивание рамки) заключается в том, что эффект де Ситтера обусловлен просто наличием центральной массы, тогда как прецессия Лензе–Тирринга обусловлена ​​вращением центральной массы. Общая прецессия вычисляется путем объединения прецессии де Ситтера с прецессией Лензе–Тирринга.

Экспериментальное подтверждение

Геодезический эффект был проверен с точностью лучше 0,5% с помощью Gravity Probe B , эксперимента, который измеряет наклон оси вращения гироскопов на орбите вокруг Земли. ^[4] Первые результаты были объявлены 14 апреля 2007 года на заседании Американского физического общества . ^[5]

Формулы

Для вывода прецессии предположим, что система находится во вращающейся метрике Шварцшильда . Невращающаяся метрика —

${\displaystyle ds^{2}=dt^{2}\left(1-{\frac {2m}{r}}\right)-dr^{2}\left(1-{\frac {2m}{r}}\right)^{-1}-r^{2}(d\theta ^{2}+\sin ^{2}\theta \,d\phi '^{2}),}$

где  с  = Г  = 1.

Введем вращающуюся систему координат с угловой скоростью , так что спутник на круговой орбите в плоскости θ = π/2 остается в состоянии покоя. Это дает нам ${\displaystyle \omega }$

${\displaystyle d\phi =d\phi '-\omega \,dt.}$

В этой системе координат наблюдатель в радиальном положении r видит вектор, расположенный в r , вращающимся с угловой частотой ω. Однако этот наблюдатель видит вектор, расположенный в некотором другом значении r , вращающимся с другой скоростью из-за релятивистского замедления времени. Преобразуя метрику Шварцшильда во вращающуюся систему отсчета и предполагая, что является константой, мы находим ${\displaystyle \theta }$

${\displaystyle {\begin{aligned}ds^{2}&=\left(1-{\frac {2m}{r}}-r^{2}\beta \omega ^{2}\right)\left(dt-{\frac {r^{2}\beta \omega }{1-2m/r-r^{2}\beta \omega ^{2}}}\,d\phi \right)^{2}-\\&-dr^{2}\left(1-{\frac {2m}{r}}\right)^{-1}-{\frac {r^{2}\beta -2mr\beta }{1-2m/r-r^{2}\beta \omega ^{2}}}\,d\phi ^{2},\end{aligned}}}$

с . Для тела, вращающегося в плоскости θ = π/2, мы будем иметь β = 1, и мировая линия тела будет сохранять постоянные пространственные координаты в течение всего времени. Теперь метрика имеет каноническую форму ${\displaystyle \beta =\sin ^{2}(\theta )}$

${\displaystyle ds^{2}=e^{2\Phi }\left(dt-w_{i}\,dx^{i}\right)^{2}-k_{ij}\,dx^{i}\,dx^{j}.}$

Из этой канонической формы мы можем легко определить скорость вращения гироскопа в собственном времени.

${\displaystyle {\begin{aligned}\Omega &={\frac {\sqrt {2}}{4}}e^{\Phi }[k^{ik}k^{jl}(\omega _{i,j}-\omega _{j,i})(\omega _{k,l}-\omega _{l,k})]^{1/2}=\\&={\frac {{\sqrt {\beta }}\omega (r-3m)}{r-2m-\beta \omega ^{2}r^{3}}}={\sqrt {\beta }}\omega .\end{aligned}}}$

где последнее равенство справедливо только для свободно падающих наблюдателей, для которых нет ускорения, и, таким образом , . Это приводит к ${\displaystyle \Phi ,_{i}=0}$

${\displaystyle \Phi ,_{i}={\frac {2m/r^{2}-2r\beta \omega ^{2}}{2(1-2m/r-r^{2}\beta \omega ^{2})}}=0.}$

Решая это уравнение относительно ω, получаем

${\displaystyle \omega ^{2}={\frac {m}{r^{3}\beta }}.}$

Это по сути закон периодов Кеплера , который оказывается релятивистски точным, если его выразить через временную координату t этой конкретной вращающейся системы координат. Во вращающейся системе отсчета спутник остается в покое, но наблюдатель на борту спутника видит, что вектор углового момента гироскопа прецессирует со скоростью ω. Этот наблюдатель также видит, что далекие звезды вращаются, но они вращаются с немного другой скоростью из-за замедления времени. Пусть τ будет собственным временем гироскопа . Тогда

${\displaystyle \Delta \tau =\left(1-{\frac {2m}{r}}-r^{2}\beta \omega ^{2}\right)^{1/2}\,dt=\left(1-{\frac {3m}{r}}\right)^{1/2}\,dt.}$

Член −2 m / r интерпретируется как гравитационное замедление времени, тогда как дополнительный − m / r обусловлен вращением этой системы отсчета. Пусть α' будет накопленной прецессией во вращающейся системе отсчета. Поскольку , прецессия в течение одной орбиты относительно далеких звезд определяется как: ${\displaystyle \alpha '=\Omega \Delta \tau }$

${\displaystyle \alpha =\alpha '+2\pi =-2\pi {\sqrt {\beta }}{\Bigg (}\left(1-{\frac {3m}{r}}\right)^{1/2}-1{\Bigg )}.}$

С помощью ряда Тейлора первого порядка находим

${\displaystyle \alpha \approx {\frac {3\pi m}{r}}{\sqrt {\beta }}={\frac {3\pi m}{r}}\sin(\theta ).}$

прецессия Томаса

Можно попытаться разложить прецессию де Ситтера на кинематический эффект, называемый прецессией Томаса , в сочетании с геометрическим эффектом, вызванным гравитационно искривленным пространством-временем. По крайней мере, один автор ^[6] описывает это таким образом, но другие утверждают, что «прецессия Томаса вступает в игру для гироскопа на поверхности Земли..., но не для гироскопа в свободно движущемся спутнике». ^[7] Возражение против первой интерпретации заключается в том, что требуемая прецессия Томаса имеет неправильный знак. Уравнение переноса Ферми-Уокера ^[8] дает как геодезический эффект, так и прецессию Томаса и описывает перенос спинового 4-вектора для ускоренного движения в искривленном пространстве-времени. Спиновый 4-вектор ортогонален 4-вектору скорости. Транспорт Ферми-Уокера сохраняет это соотношение. Если ускорения нет, транспорт Ферми-Уокера представляет собой просто параллельный перенос вдоль геодезической и дает спиновую прецессию из-за геодезического эффекта. Для ускорения, вызванного равномерным круговым движением в плоском пространстве-времени Минковского, транспорт Ферми-Уокера дает прецессию Томаса.

Смотрите также

• Перетаскивание кадров
• Геодезические в общей теории относительности
• Гравитационный колодец
• Хронология гравитационной физики и теории относительности

Примечания

1. Жан Эйзенштадт; Энн Дж. Кокс (1988). Исследования по истории общей теории относительности. Биркхойзер . п. 42. ИСБН 0-8176-3479-7.
2. de Sitter, W (1916). «О теории гравитации Эйнштейна и ее астрономических следствиях». Mon. Not. R. Astron. Soc . 77 : 155–184. Bibcode :1916MNRAS..77..155D. doi : 10.1093/mnras/77.2.155 .
3. Риндлер, стр. 254.
4. Эверитт, CWF; Паркинсон, BW (2009). "Результаты научных исследований Gravity Probe B — Заключительный отчет НАСА" (PDF) . Получено 2009-05-02 .
5. Кан, Боб (14 апреля 2007 г.). «Был ли прав Эйнштейн? Ученые впервые публично представили результаты Gravity Probe B» (PDF) . Stanford News . Получено 3 января 2023 г. .
6. Риндлер, Страница 234
7. Мизнер, Торн и Уилер, Гравитация, стр. 1118.
8. Мизнер, Торн и Уилер, Гравитация, стр. 165, стр. 175-176, стр. 1117-1121

Ссылки

• Вольфганг Риндлер (2006) Относительность: специальная, общая и космологическая (2-е изд.), Oxford University Press, ISBN 978-0-19-856731-8 

Внешние ссылки

• Веб-сайты Gravity Probe B в НАСА и Стэнфордском университете
• Прецессия в искривленном пространстве «Геодезический эффект»
• Геодезический эффект