Теорема Мора–Маскерони

В математике теорема Мора-Маскерони гласит, что любое геометрическое построение, которое можно выполнить с помощью циркуля и линейки, можно выполнить с помощью одного циркуля.

Необходимо понимать, что «любая геометрическая конструкция» относится к фигурам, которые не содержат прямых линий, поскольку очевидно, что невозможно нарисовать прямую линию без линейки. Подразумевается, что линия определяется при условии, что на этой линии даны или построены две различные точки, даже если визуального представления линии не будет. Теорему можно сформулировать точнее: ^[1]

Любое евклидово построение, поскольку заданными и требуемыми элементами являются точки (или окружности), может быть завершено с помощью одного циркуля, если оно может быть завершено с помощью как циркуля, так и линейки одновременно.

Хотя использование линейки может значительно облегчить построение, теорема показывает, что любой набор точек, который полностью определяет построенную фигуру, может быть определен с помощью одного лишь циркуля, и единственная причина использования линейки — эстетика, позволяющая видеть прямые линии, что для целей построения функционально не нужно.

История

Первоначально результат был опубликован Георгом Мором в 1672 году ^[2] , но его доказательство оставалось в безвестности до 1928 года. ^[3]^[4]^[5] Теорема была независимо открыта Лоренцо Маскерони в 1797 году и была известна как теорема Маскерони, пока работа Мора не была переоткрыта. ^[6]

Известно несколько доказательств результата. Доказательство Маскерони 1797 года в целом основывалось на идее использования отражения относительно прямой в качестве основного инструмента. Решение Мора было иным. ^[3] В 1890 году Август Адлер опубликовал доказательство, использующее преобразование инверсии . ^[7]

Алгебраический подход использует изоморфизм между евклидовой плоскостью и действительным координатным пространством . Таким образом, в 1990 году была доказана более сильная версия теоремы. ^[8] Также показана зависимость теоремы от аксиомы Архимеда (которая не может быть сформулирована на языке первого порядка ). $\mathbb {R} ^{2}$

Конструктивное доказательство

Контур

Для доказательства теоремы необходимо доказать возможность каждой из основных конструкций циркуля и линейки с использованием только циркуля, поскольку они являются основами или элементарными шагами для всех других конструкций. Это:

Создание линии через две существующие точки
Создание окружности через одну точку с центром в другой точке
Создание точки, которая является пересечением двух существующих непараллельных линий.
Создание одной или двух точек на пересечении линии и окружности (если они пересекаются)
Создание одной или двух точек на пересечении двух окружностей (если они пересекаются).

#1 — Линия, проходящая через две точки

Понятно, что прямую линию нельзя провести без линейки. Считается, что линия задана любыми двумя точками, поскольку любая такая пара определяет уникальную линию. В соответствии с целью теоремы, которую мы стремимся доказать, фактическая линия не обязательно должна быть проведена, но по эстетическим причинам.

#2 — Окружность, проходящая через одну точку с определенным центром

Это можно сделать с помощью одного циркуля. Линейка для этого не требуется.

#5 - Пересечение двух окружностей

Эту конструкцию можно также выполнить непосредственно с помощью циркуля.

#3, #4 - Другие конструкции

Таким образом, для доказательства теоремы необходимо привести только конструкции, построенные с использованием только циркуля, для пунктов 3 и 4.

Обозначения и примечания

В этой статье будут использоваться следующие обозначения. Окружность, центр которой находится в точке $U$ и которая проходит через точку $V,$ будет обозначаться как $U (V)$ . Окружность с центром $U$ и радиусом, заданным числом $r$ , или отрезком $AB$ будет обозначаться как $U (r)$ или $U (AB)$ , соответственно. ^[9]

В общих конструкциях часто есть несколько вариаций, которые дадут тот же результат. Выбор, сделанный в таком варианте, может быть сделан без потери общности. Однако, когда конструкция используется для доказательства того, что что-то может быть сделано, нет необходимости описывать все эти различные варианты, и для ясности изложения ниже будет приведен только один вариант. Однако многие конструкции имеют разные формы в зависимости от того, используют ли они инверсию окружности или нет, и эти альтернативы будут приведены, если это возможно.

Также важно отметить, что некоторые из приведенных ниже конструкций, доказывающих теорему Мора–Маскерони, требуют произвольного размещения точек в пространстве, например, нахождения центра окружности, когда он еще не указан (см. конструкцию ниже). В некоторых парадигмах построения, например, в геометрическом определении конструктивного числа , произвольное размещение точек может быть запрещено. Однако в такой парадигме, например, существуют различные конструкции, так что произвольное размещение точек необязательно. Также стоит отметить, что ни один круг не может быть построен без циркуля, поэтому на практике нет причин, по которым центральная точка не должна существовать.

Некоторые предварительные построения

Для доказательства приведенных выше конструкций #3 и #4, которые включены ниже, ниже также объясняются несколько необходимых промежуточных конструкций, поскольку они часто используются и на них ссылаются. Это также конструкции только с компасом. Все конструкции ниже опираются на #1,#2,#5 и любую другую конструкцию, которая указана до нее.

Теорема эквивалентности компаса (перенос окружности)

Возможность переноса или копирования окружности в новый центр жизненно важна в этих доказательствах и является основополагающей для установления достоверности теоремы. Создание новой окружности с тем же радиусом, что и у первой, но с центром в другой точке, является ключевой особенностью, отличающей разрушающийся циркуль от современного жесткого циркуля. С жестким циркулем это тривиально, но с разрушающимся циркулем это вопрос возможности построения. Эквивалентность разрушающегося циркуля и жесткого циркуля была доказана Евклидом (Книга I, Предложение 2 «Начал» ) с помощью линейки и разрушающегося циркуля, когда он, по сути, строит копию окружности с другим центром. Эта эквивалентность также может быть установлена с помощью одного (разрушающегося) циркуля, доказательство которого можно найти в основной статье.

Отражение точки относительно прямой

Даны отрезок $AB$ и точка $C,$ не лежащая на прямой, определяемой этим отрезком. Постройте изображение точки $C$ при отражении относительно этой прямой.

Постройте две окружности: одну с центром в точке $A$ , а другую с центром в точке $B$ , обе проходящие через $точку C.$
D , другая точка пересечения двух окружностей, является отражением C относительно линии AB .
- Если $C = D$ (то есть существует единственная точка пересечения двух окружностей), то $C$ является своим собственным отражением и лежит на прямой $AB$ (вопреки предположению), и две окружности являются внутренними касательными.

Увеличение длины отрезка линии

Дан отрезок $AB.$ Найдите точку $C$ на линии $AB$ так, чтобы $B$ была серединой отрезка $AC$ . ^[10]

Постройте точку $D$ как пересечение окружностей $A (B)$ и $B (A)$ . (∆ ABD — равносторонний треугольник.)
Постройте точку $E \neq A$ как пересечение окружностей $D (B)$ и $B (D)$ . (∆ DBE — равносторонний треугольник.)
Наконец, построим точку $C \neq D$ как пересечение окружностей $B (E)$ и $E (B)$ . (∆ EBC — равносторонний треугольник, а три угла при $B$ показывают, что $A, B и C$ лежат на одной прямой.)

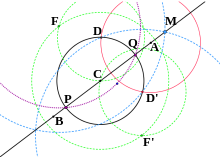
Это построение можно повторять столько раз, сколько необходимо, чтобы найти точку $Q,$ такую, что длина отрезка $AQ$ = $n$ ⋅ длина отрезка $AB$ для любого положительного целого числа $n$ .

Инверсия в круге

Даны окружность $B (r)$ для некоторого радиуса $r$ (черного цвета) и точка $D (\neq B) и$ построим точку $I$ , которая является инверсией $D$ в окружности. ^[11] Естественно, для точки инверсии не существует . ${\textstyle Д=Б}$

Нарисуйте круг $D (B)$ (красного цвета).
Предположим, что красный круг пересекает черный круг в точках E и E'.
- если окружности не пересекаются в двух точках, см. ниже альтернативное построение.
- если окружности пересекаются только в одной точке, то их можно инвертировать, просто удвоив длину (учтиво увеличив длину ). $E=E'$ $D$ $ЭБ$ $БД$
Отразим центр окружности относительно прямой : $Б$ $EE'$
1. Постройте два новых круга $E (B)$ и $E' (B)$ (светло-голубого цвета).
2. Голубые круги пересекаются в точке $B$ и в другой точке $I \neq B.$
Точка $I$ — это искомая инверсия $D$ в черном круге.

Точка $I$ такова, что радиус $r$ точки $B (r)$ относится к $IB$ так же, как $DB$ относится к радиусу; или $IB / r = r / DB$ .

В случае, если приведенное выше построение не удается (то есть красный круг и черный круг не пересекаются в двух точках), ^[10] найдите точку $Q$ на линии $BD$ так, чтобы длина отрезка $BQ$ была положительным целым кратным, скажем, $n$ , длины $BD$ и была больше $r / 2$ (это возможно по аксиоме Архимеда). Найдите $Q',$ обратную $Q$ в окружности $B (r),$ как указано выше (красный и черный круги теперь должны пересекаться в двух точках). Точка $I$ теперь получается путем расширения $BQ'$ так, чтобы $BI$ = $n \cdot BQ'$ .

Определение центра окружности через три точки

Даны три неколлинеарные точки $A$ , $B$ и $C$ , найдите центр $O$ окружности, которую они определяют. ^[12]

Постройте точку $D$ , обратную точке $C,$ в окружности $A (B)$ .
Отразим точку $A$ от прямой $BD$ в точку $X.$
$O$ — это обратная точка $X$ в круге $A (B)$ .

Пересечение двух непараллельных прямых (конструкция №3)

Даны непараллельные прямые $AB$ и $CD$ , найдите их точку пересечения $X.$ ^[12 ]

Выберите окружность $O (r)$ произвольного радиуса, центр $O$ которой не лежит ни на одной из прямых.
Переставим точки $A$ и $B$ в окружности $O (r)$ в точки $A'$ и $B'$ соответственно.
Прямая $AB$ инвертируется в окружность, проходящую через $O$ , $A'$ и $B'$ . Найдите центр $E$ этой окружности.
Переставим точки $C$ и $D$ в окружности $O (r)$ в точки $C'$ и $D'$ соответственно.
Прямая $CD$ переворачивается в окружность, проходящую через $O$ , $C'$ и $D'$ . Найдите центр $F$ этой окружности.
Пусть $Y \neq O$ — пересечение окружностей $E (O)$ и $F (O)$ .
$X$ — это обратная точка $Y$ в круге $O (r)$ .

Пересечение прямой и окружности (конструкция №4)

Построение точек пересечения прямой и окружности с помощью одного лишь циркуля распадается на два случая в зависимости от того, является ли центр окружности коллинеарным с прямой или нет.

Центр окружности не лежит на одной прямой с линией

Предположим, что центр окружности не лежит на прямой.

Пересечение прямой и окружности (случай неколлинеарности)

Даны окружность $C (r)$ (черная) и линия $AB$ . Мы хотим построить точки пересечения $P$ и $Q$ между ними (если они существуют). ^[13]^[3]

Постройте точку D , которая является отражением точки C относительно линии AB . (См. выше.)
- В предположении этого случая $C \neq D.$
Постройте окружность $D (r)$ (красного цвета). (См. выше эквивалентность циркуля.)
Пересечения окружности C ( r ) и новой красной окружности D ( r ) являются точками P и Q.
- Если две окружности касаются (внешне), то . $P=Q$
  - Внутреннее касание невозможно.
- Если две окружности не пересекаются, то и окружность с линией не пересекаются.
Точки P и Q являются точками пересечения окружности C ( r ) и прямой AB .
- Если , то прямая касается окружности . $P=Q$ $C(r)$

Можно также предложить альтернативную конструкцию, использующую инверсию круга. ^[12]

Даны окружность $C (r)$ и прямая $AB$ . Мы хотим построить точки пересечения $P$ и $Q$ между ними (если они существуют).

Перевернем точки A и B в окружности C ( r ) на точки A' и B' соответственно.
- В предположении этого случая точки $A'$ , $B'$ и $C$ не лежат на одной прямой.
Найдите центр $E$ окружности, проходящей через точки $C$ , $A'$ и $B'$ .
Постройте окружность $E (C)$ , которая представляет собой инверсию прямой $AB$ в окружность $C (r)$ .
P и Q — точки пересечения окружностей C ( r ) и E ( C ) . ^[14]
- Если две окружности (внутренне) касаются , то и прямая также является касательной. $P=Q$

Центр окружности лежит на одной прямой с линией

Дан круг $C (D),$ центр $C$ которого лежит на прямой $AB$ , найдите точки $P$ и $Q$ , точки пересечения круга и прямой. ^[15]

Постройте точку $D' \neq D$ как другое пересечение окружностей $A (D)$ и $C (D)$ .
Постройте точку $F$ как пересечение окружностей $C (DD')$ и $D (C)$ . ( $F$ — четвертая вершина параллелограмма $CD'DF$ .)
Постройте точку $F'$ как пересечение окружностей $C (DD')$ и $D' (C)$ . ( $F'$ - четвертая вершина параллелограмма $CDD'F'$ .)
Постройте точку $M$ как пересечение окружностей $F (D')$ и $F' (D)$ . ( $M$ лежит на $AB$ .)
Точки $P$ и $Q$ являются пересечениями окружностей $F (CM)$ и $C (D)$ .

Таким образом, было показано, что все основные построения, которые можно выполнить с помощью линейки и циркуля, можно выполнить с помощью одного циркуля, при условии, что линия не может быть буквально нарисована, а может быть просто определена двумя точками.

Другие типы ограниченного строительства

Ограничения, связанные с компасом

Математики эпохи Возрождения Лодовико Феррари , Джероламо Кардано , Никколо Фонтана Тарталья и другие смогли показать в XVI веке, что любое построение с помощью линейки и циркуля можно выполнить с помощью линейки и циркуля фиксированной ширины (т. е. ржавого циркуля). ^[16]

Теорема эквивалентности циркуля показывает , что во всех конструкциях, упомянутых выше, знакомый современный компас с его фиксируемой апертурой, который может быть использован для передачи расстояний, может быть заменен на «складной компас», компас, который складывается, когда его поднимают со страницы, так что его нельзя напрямую использовать для передачи расстояний. Действительно, оригинальные конструкции Евклида используют складной компас. Можно перевести любой круг на плоскости с помощью складного циркуля, используя не более трех дополнительных применений циркуля сверх того, что есть у жесткого циркуля.

Ограничения, за исключением компаса

Мотивированный результатом Маскерони, в 1822 году Жан Виктор Понселе выдвинул гипотезу о вариации на ту же тему. Его работа проложила путь для области проективной геометрии , в которой он предположил, что любое построение, возможное с помощью линейки и циркуля, может быть выполнено с помощью одной только линейки. Однако, одно условие заключается в том, что должно быть указано не менее одной окружности с указанным центром. Это утверждение, теперь известное как теорема Понселе–Штайнера , было доказано Якобом Штайнером одиннадцать лет спустя.

Доказательство, представленное позднее в 1904 году Франческо Севери , смягчает требование о наличии одной полной окружности и показывает, что любая малая дуга окружности, при условии, что центр все еще присутствует, по-прежнему достаточна. ^[17]

Кроме того, сам центр может быть опущен вместо частей дуги, если он заменен чем-то другим достаточным, например, второй концентрической окружностью, второй пересекающейся окружностью или третьей окружностью на плоскости. В качестве альтернативы, вторая окружность, которая не является ни пересекающейся, ни концентрической, является достаточной, при условии, что задана точка либо на центральной линии, проходящей через них, либо на радикальной оси между ними, или на плоскости существуют две параллельные прямые. Одна окружность без своего центра также может быть достаточной при правильных обстоятельствах. Могут существовать и другие уникальные условия.

Смотрите также

Примечания

↑ Ивс 1963, стр. 201
^ Георг Мор, Евклид Даник (Амстердам: Якоб ван Велсен, 1672).
^ abc Eves 1963, стр. 199
^ Hjelmslev, J. (1928) «Om et af den danske matematiker Georg Mohr udgivet skrift Euclides Danicus , udkommet i Amsterdam i 1672» [Из мемуаров Euclides Danicus, опубликованных датским математиком Георгом Мором в 1672 году в Амстердаме], Matematisk Tidsskrift B , страницы 1–7.
^ Шогт, JH (1938) « Евклид Даник Ом Георга Мора », Matematisk Tidsskrift A, страницы 34–36.
^ Лоренцо Маскерони, La Geometria del Compasso (Павия: Пьетро Галеацци, 1797). Издание 1901 года.
↑ Ивс 1963, стр. 198
↑ Арнон Аврон , «О строгой сильной конструктивности с помощью одного циркуля», Журнал геометрии (1990) 38: 12.
↑ Ивс 1963, стр. 184
^ ab Pedoe 1988, стр. 78
^ Педоу 1988, стр. 77
^ abc Pedoe 1988, стр. 123
^ Хунгербюлер 1994, стр. 784
^ Педоу выполняет еще одну инверсию в этой точке, но точки $P$ и $Q$ находятся на окружности инверсии и поэтому инвариантны относительно этой последней ненужной инверсии.
↑ Ивс 1963, стр. 200
^ Ретц, Мерлин; Кейн, Мета Дарлин (1989), «Построения с помощью циркуля и линейки», Исторические темы для уроков математики , Национальный совет учителей математики (NCTM), стр. 195, ISBN 9780873532815
^ Ретц и Кейн 1989, стр. 196

Ссылки

Ивс, Говард (1963), Обзор геометрии (Том первый) , Аллин и Бэкон
Хунгербюлер, Норберт (1994), «Краткое элементарное доказательство теоремы Мора–Маскерони», The American Mathematical Monthly , 101 (8): 784–787, doi :10.1080/00029890.1994.11997027
Педоу, Дэн (1988) [1970], Геометрия / Полный курс , Довер, ISBN 978-0-486-65812-4

Дальнейшее чтение

Педоу, Дэн (1995) [1957], «1 Раздел 11: Геометрия циркуля», Окружности / Математический взгляд , Математическая ассоциация Америки, стр. 23–25, ISBN 978-0-88385-518-8
Посаментье, Альфред С.; Геретшлегер, Роберт (2016), «8. Построения Маскерони с использованием только циркуля», The Circle , Prometheus Books, стр. 197–216, ISBN 978-1-63388-167-9

Внешние ссылки

Строительство только с помощью компаса