Искусственный нейрон

Математическая функция, задуманная как грубая модель

Искусственная структура нейрона

Искусственный нейрон — это математическая функция, задуманная как модель биологических нейронов в нейронной сети . Искусственные нейроны — это элементарные единицы искусственных нейронных сетей . ^[1] Искусственный нейрон — это функция, которая получает один или несколько входов, применяет веса к этим входам и суммирует их для получения выходных данных.

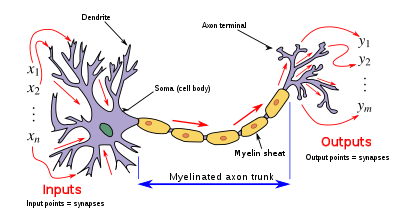
Дизайн искусственного нейрона был вдохновлен нейронной схемой . Его входы аналогичны возбуждающим постсинаптическим потенциалам и тормозным постсинаптическим потенциалам на нейронных дендритах , илиактивация , ее вес аналогичен синаптическому весу , а ее выход аналогичен потенциалу действия нейрона, который передается по его аксону .

Обычно каждый вход взвешивается отдельно , и сумма часто добавляется к термину, известному как смещение (приблизительно соответствующему пороговому потенциалу ), перед тем, как пройти через нелинейную функцию, известную как функция активации или передаточная функция ^{[ необходимо разъяснение ]} . Передаточные функции обычно имеют сигмоидальную форму , но они также могут принимать форму других нелинейных функций, кусочно -линейных функций или ступенчатых функций. Они также часто монотонно возрастают , непрерывны , дифференцируемы и ограничены . Также недавно были исследованы немонотонные, неограниченные и осциллирующие функции активации с несколькими нулями, которые превосходят сигмоидальные и ReLU-подобные функции активации во многих задачах. Пороговая функция вдохновила на создание логических вентилей, называемых пороговой логикой; применима для создания логических схем, напоминающих обработку мозгом. Например, новые устройства, такие как мемристоры, широко использовались для разработки такой логики в последнее время. ^[2]

Передаточную функцию искусственного нейрона не следует путать с передаточной функцией линейной системы .

Искусственный нейрон может называться полулинейным блоком , Nv-нейроном , бинарным нейроном , линейной пороговой функцией или нейроном Маккалока–Питтса ( MCP ) , в зависимости от используемой структуры.

Простые искусственные нейроны, такие как модель Маккалока–Питтса, иногда описываются как «карикатурные модели», поскольку они призваны отражать одно или несколько нейрофизиологических наблюдений, но без учета реализма. ^[3] Искусственные нейроны могут также относиться к искусственным клеткам в нейроморфной инженерии ( см. ниже ), которые похожи на естественные физические нейроны.

Базовая структура

Для данного искусственного нейрона k пусть будет m  + 1 входов с сигналами x ₀ через x _m и весами w _{k 0} через w _{k m} . Обычно входу x ₀ присваивается значение +1, что делает его смещенным входом с w _{k 0}  =  b _k . Это оставляет только m фактических входов для нейрона: от x ₁ до x _m .

Выход k -го нейрона:

${\displaystyle y_{k}=\varphi \left(\sum _{j=0}^{m}w_{kj}x_{j}\right)}$

Где (фи) — передаточная функция (обычно пороговая функция). ${\displaystyle \varphi }$

Выход аналогичен аксону биологического нейрона, и его значение распространяется на вход следующего слоя через синапс. Он также может выйти из системы, возможно, как часть выходного вектора .

Он не имеет процесса обучения как такового. Его передаточные функции весов вычисляются, а пороговое значение предопределено.

Нейрон Маккалока-Питтса (MCP)

Нейрон MCP — это своего рода ограниченный искусственный нейрон, который работает дискретными временными шагами. Каждый имеет ноль или более входов и записывается как . Он имеет один выход, записывается как . Каждый вход может быть возбуждающим или тормозным . Выход может быть либо тихим , либо активирующим . Нейрон MCP также имеет порог . ${\displaystyle x_{1},...,x_{n}}$ ${\displaystyle y}$ ${\displaystyle b\in \{0,1,2,...\}}$

В нейронной сети MCP все нейроны работают в синхронных дискретных временных шагах . В момент времени выход нейрона равен , если число активирующих возбуждающих входов по крайней мере равно пороговому значению, и не активируются никакие тормозящие входы; в противном случае. ${\displaystyle t=0,1,2,3,...}$ ${\displaystyle t+1}$ ${\displaystyle y(t+1)=1}$ ${\displaystyle y(t+1)=0}$

Каждый выход может быть входом для произвольного числа нейронов, включая себя самого (то есть возможны самопетли). Однако выход не может соединяться с одним нейроном более одного раза. Самопетли не вызывают противоречий, поскольку сеть работает в синхронных дискретных временных шагах.

В качестве простого примера рассмотрим один нейрон с порогом 0 и один ингибирующий самоцикл. Его выход будет колебаться между 0 и 1 на каждом шаге, действуя как «часы».

Любой конечный автомат может быть смоделирован нейронной сетью MCP. ^[4] При наличии бесконечной ленты нейронные сети MCP могут смоделировать любую машину Тьюринга . ^[5]

Биологические модели

Нейрон и миелинизированный аксон с потоком сигнала от входов на дендритах к выходам на окончаниях аксона

Искусственные нейроны разработаны для имитации аспектов их биологических аналогов. Однако существует значительный разрыв в производительности между биологическими и искусственными нейронными сетями. В частности, были обнаружены отдельные биологические нейроны в человеческом мозге с осциллирующей функцией активации, способные обучаться функции XOR . ^[6]

• Дендриты – В биологическом нейроне дендриты действуют как входной вектор. Эти дендриты позволяют клетке получать сигналы от большого (>1000) числа соседних нейронов. Как и в приведенной выше математической обработке, каждый дендрит способен выполнять «умножение» на «весовое значение» этого дендрита. Умножение достигается путем увеличения или уменьшения соотношения синаптических нейротрансмиттеров к сигнальным химикатам, введенным в дендрит в ответ на синаптический нейротрансмиттер. Отрицательный эффект умножения может быть достигнут путем передачи ингибиторов сигнала (т. е. противоположно заряженных ионов) вдоль дендрита в ответ на прием синаптических нейротрансмиттеров.
• Сома – В биологическом нейроне сома действует как функция суммирования, как видно из приведенного выше математического описания. Когда положительные и отрицательные сигналы (возбуждающие и ингибирующие соответственно) поступают в сому из дендритов, положительные и отрицательные ионы эффективно суммируются, просто смешивая их в растворе внутри тела клетки.
• Аксон – Аксон получает свой сигнал от суммационного поведения, которое происходит внутри сомы. Открытие аксона по сути замеряет электрический потенциал раствора внутри сомы. Как только сома достигает определенного потенциала, аксон будет передавать импульс сигнала all-in по всей своей длине. В этом отношении аксон ведет себя как способность для нас соединять наш искусственный нейрон с другими искусственными нейронами.

Однако, в отличие от большинства искусственных нейронов, биологические нейроны срабатывают дискретными импульсами. Каждый раз, когда электрический потенциал внутри сомы достигает определенного порога, по аксону передается импульс. Эту пульсацию можно перевести в непрерывные значения. Скорость (активаций в секунду и т. д.), с которой срабатывает аксон, напрямую преобразуется в скорость, с которой соседние клетки получают сигнальные ионы, вводимые в них. Чем быстрее срабатывает биологический нейрон, тем быстрее соседние нейроны накапливают электрический потенциал (или теряют электрический потенциал, в зависимости от «веса» дендрита, который соединяется с сработавшим нейроном). Именно это преобразование позволяет компьютерным ученым и математикам моделировать биологические нейронные сети с использованием искусственных нейронов, которые могут выводить различные значения (часто от −1 до 1).

Кодирование

Исследования показали, что унарное кодирование используется в нейронных цепях, ответственных за производство птичьего пения . ^{[7] [8]} Использование унарного кодирования в биологических сетях, предположительно, обусловлено присущей ему простотой кодирования. Другим способствующим фактором может быть то, что унарное кодирование обеспечивает определенную степень исправления ошибок. ^[9]

Физические искусственные клетки

Ведутся исследования и разработки физических искусственных нейронов — органических и неорганических.

Например, некоторые искусственные нейроны могут получать ^{[10] [11]} и высвобождать дофамин ( химические сигналы, а не электрические сигналы) и взаимодействовать с естественными мышечными и мозговыми клетками крысы , что может быть использовано в нейрокомпьютерных интерфейсах / протезировании . ^{[12] [13]}

Маломощные биосовместимые мемристоры могут позволить создавать искусственные нейроны, которые функционируют при напряжениях биологических потенциалов действия и могут использоваться для прямой обработки биосенсорных сигналов , для нейроморфных вычислений и/или прямой связи с биологическими нейронами . ^{[14] [15] [16]}

Органические нейроморфные схемы, изготовленные из полимеров , покрытых гелем, богатым ионами, чтобы материал мог переносить электрический заряд, как настоящие нейроны , были встроены в робота, что позволяет ему обучаться сенсомоторно в реальном мире, а не посредством моделирования или виртуально. ^{[17] [18]} Более того, искусственные спайковые нейроны, изготовленные из мягкой материи (полимеров), могут работать в биологически релевантных средах и обеспечивать синергетическую связь между искусственными и биологическими доменами. ^{[19] [20]}

История

Первым искусственным нейроном была пороговая логическая единица (TLU) или линейная пороговая единица ^[21] , впервые предложенная Уорреном Маккалоком и Уолтером Питтсом в 1943 году в работе «Логическое исчисление идей, имманентных нервной деятельности ». Модель была специально разработана как вычислительная модель «нервной сети» в мозге. ^[22] В качестве передаточной функции она использовала порог, эквивалентный использованию ступенчатой ​​функции Хевисайда . Первоначально рассматривалась только простая модель с бинарными входами и выходами, некоторыми ограничениями на возможные веса и более гибким пороговым значением. С самого начала было замечено, что любая булева функция может быть реализована сетями таких устройств, что легко увидеть из того факта, что можно реализовать функции И и ИЛИ и использовать их в дизъюнктивной или конъюнктивной нормальной форме . Исследователи также вскоре поняли, что циклические сети с обратными связями через нейроны могут определять динамические системы с памятью, но большая часть исследований была сосредоточена (и до сих пор сосредоточена) на строго прямых сетях из- за меньшей сложности, которую они представляют.

Одной из важных и новаторских искусственных нейронных сетей, которая использовала линейную пороговую функцию, был персептрон , разработанный Фрэнком Розенблаттом . Эта модель уже рассматривала более гибкие значения веса в нейронах и использовалась в машинах с адаптивными возможностями. Представление пороговых значений как смещающего термина было введено Бернардом Видроу в 1960 году – см. ADALINE .

В конце 1980-х годов, когда исследования нейронных сетей вновь набрали силу, начали рассматривать нейроны с более непрерывными формами. Возможность дифференциации функции активации позволяет напрямую использовать градиентный спуск и другие алгоритмы оптимизации для корректировки весов. Нейронные сети также начали использоваться в качестве общей модели аппроксимации функций . Самый известный алгоритм обучения, называемый обратным распространением, был переоткрыт несколько раз, но его первая разработка восходит к работе Пола Вербоса . ^{[23] [24]}

Типы передаточных функций

Функция передачи ( функция активации ) нейрона выбирается так, чтобы иметь ряд свойств, которые либо улучшают, либо упрощают сеть, содержащую нейрон. Важно, например, что любой многослойный персептрон, использующий линейную функцию передачи, имеет эквивалентную однослойную сеть; поэтому для получения преимуществ многослойной сети необходима нелинейная функция. ^{[ необходима цитата ]}

Ниже во всех случаях u относится к взвешенной сумме всех входов нейрона, т.е. для n входов,

${\displaystyle u=\sum _{i=1}^{n}w_{i}x_{i}}$

где w — вектор синаптических весов , а x — вектор входов.

Ступенчатая функция

Выход y этой передаточной функции является двоичным, в зависимости от того, соответствует ли вход заданному порогу θ . «Сигнал» отправляется, т. е. выход устанавливается в единицу, если активация соответствует порогу.

${\displaystyle y={\begin{cases}1&{\text{if }}u\geq \theta \\0&{\text{if }}u<\theta \end{cases}}}$

Эта функция используется в персептронах и часто появляется во многих других моделях. Она выполняет разделение пространства входов гиперплоскостью . Она особенно полезна в последнем слое сети, предназначенной для выполнения бинарной классификации входов. Ее можно аппроксимировать из других сигмоидальных функций, присваивая большие значения весам.

Линейная комбинация

В этом случае выходной блок — это просто взвешенная сумма его входов плюс смещение . Ряд таких линейных нейронов выполняют линейное преобразование входного вектора. Обычно это более полезно в первых слоях сети. Существует ряд инструментов анализа, основанных на линейных моделях, таких как гармонический анализ , и все они могут использоваться в нейронных сетях с этим линейным нейроном. Смещение позволяет нам выполнять аффинные преобразования данных.

См.: Линейное преобразование , Гармонический анализ , Линейный фильтр , Вейвлет , Анализ главных компонент , Анализ независимых компонент , Деконволюция .

Сигмовидная кишка

Довольно простая нелинейная функция, сигмоидальная функция , такая как логистическая функция, также имеет легко вычисляемую производную, которая может быть важна при расчете обновлений веса в сети. Таким образом, она делает сеть более управляемой математически и была привлекательна для ранних компьютерных ученых, которым нужно было минимизировать вычислительную нагрузку своих симуляций. Ранее она часто встречалась в многослойных персептронах . Однако недавние исследования показали, что сигмоидальные нейроны менее эффективны, чем выпрямленные линейные нейроны. Причина в том, что градиенты, вычисляемые алгоритмом обратного распространения, имеют тенденцию уменьшаться до нуля по мере распространения активаций через слои сигмоидальных нейронов, что затрудняет оптимизацию нейронных сетей с использованием нескольких слоев сигмоидальных нейронов.

Выпрямитель

В контексте искусственных нейронных сетей выпрямитель или ReLU (Rectified Linear Unit) представляет собой функцию активации, определяемую как положительная часть ее аргумента:

${\displaystyle f(x)=x^{+}=\max(0,x),}$

где x — вход нейрона. Это также известно как функция рампы и аналогично полуволновому выпрямлению в электротехнике. Эта функция активации была впервые введена в динамическую сеть Ханлозером и др. в статье 2000 года в Nature ^[25] с сильными биологическими мотивами и математическими обоснованиями. ^[26] Впервые было продемонстрировано в 2011 году, что она позволяет лучше обучать более глубокие сети, ^[27] по сравнению с широко используемыми функциями активации до 2011 года, т. е. логистической сигмоидой (которая вдохновлена ​​теорией вероятностей ; см. логистическая регрессия ) и ее более практичным ^[28] аналогом, гиперболическим тангенсом .

Распространенным вариантом функции активации ReLU является Leaky ReLU, которая допускает небольшой положительный градиент, когда блок неактивен:

${\displaystyle f(x)={\begin{cases}x&{\text{if }}x>0,\\ax&{\text{otherwise}}.\end{cases}}}$

где x — входной сигнал нейрона, а a — небольшая положительная константа (в оригинальной статье для a использовалось значение 0,01 ). ^[29]

Алгоритм псевдокода

Ниже приведена простая реализация псевдокода ^{[ требуется ссылка ]} одного TLU, который принимает логические входные данные (истина или ложь) и возвращает один логический выходной сигнал при активации. Используется объектно-ориентированная модель. Метод обучения не определен, поскольку существует несколько. Если бы использовалась чисто функциональная модель, класс TLU ниже был бы заменен функцией TLU с входными параметрами threshold, weights и inputs, которая возвращала бы логическое значение.

класс TLU определяется как: порог элемента данных : число весов элементов данных : список чисел размера X функциональный член fire(входные данные : список логических значений размера X) : логическое значение, определенное как:  переменная T : число T ← 0 для каждого i от 1 до X do  if inputs(i) is true then T ← T + weights(i) end if  end for each  if T > threshold then  return true else:  return false end if  end function end class

Смотрите также

• Связывающий нейрон
• Коннекционизм

Ссылки

1. Рами А. Альзахрани; Элис К. Паркер. «Нейроморфные схемы с нейронной модуляцией, улучшающие информационное содержание нейронных сигналов». Труды Международной конференции по нейроморфным системам 2020 г. Статья 19. Нью-Йорк: Ассоциация вычислительной техники. doi : 10.1145/3407197.3407204 . ISBN 978-1-4503-8851-1. S2CID  220794387.
2. Maan, AK; Jayadevi, DA; James, AP (1 января 2016 г.). «Обзор пороговых логических схем памяти». IEEE Transactions on Neural Networks and Learning Systems . PP (99): 1734–1746. arXiv : 1604.07121 . Bibcode : 2016arXiv160407121M. doi : 10.1109/TNNLS.2016.2547842. ISSN  2162-237X. PMID  27164608. S2CID  1798273.
3. FC Hoppensteadt и EM Izhikevich (1997). Слабосвязанные нейронные сети . Springer. стр. 4. ISBN 978-0-387-94948-2.
4. Минский, Марвин Ли (1967-01-01). Вычисления: Конечные и бесконечные машины . Prentice Hall. ISBN 978-0-13-165563-8.
5. Маккалок, Уоррен С.; Питтс, Уолтер (1943-12-01). «Логическое исчисление идей, имманентных нервной деятельности». Бюллетень математической биофизики . 5 (4): 115–133. doi :10.1007/BF02478259. ISSN  1522-9602.
6. Гидон, Альберт; Зольник, Тимоти Адам; Фидзинский, Павел; Болдуан, Феликс; Папуци, Афанасия; Poirazi, Панайота ; Хольткамп, Мартин; Вида, Имре; Ларкум, Мэтью Эван (03 января 2020 г.). «Дендритные потенциалы действия и вычисления в нейронах коры головного мозга 2/3 слоя человека». Наука . 367 (6473): 83–87. Бибкод : 2020Sci...367...83G. дои : 10.1126/science.aax6239 . PMID  31896716. S2CID  209676937.
7. Сквайр, Л.; Олбрайт, Т.; Блум, Ф.; Гейдж, Ф.; Спитцер, Н., ред. (октябрь 2007 г.). Модели нейронных сетей для создания, обучения и кодирования пения птиц (PDF) . Новая энциклопедия нейронауки: Elservier. Архивировано из оригинала (PDF) 2015-04-12 . Получено 12 апреля 2015 г. .
8. Мур, Дж. М.; и др. (2011). «Конвергенция моторных путей предсказывает размер репертуара слогов у певчих птиц». Proc. Natl. Acad. Sci. USA . 108 (39): 16440–16445. Bibcode : 2011PNAS..10816440M. doi : 10.1073/pnas.1102077108 . PMC 3182746. PMID  21918109 . 
9. Потлури, Пушпа Шри (26 ноября 2014 г.). «Возможность исправления ошибок унарного кодирования». arXiv : 1411.7406 [cs.IT].
10. Кляйнер, Курт (25 августа 2022 г.). «Заставить компьютерные чипы действовать больше как мозговые клетки». Журнал Knowable | Annual Reviews . doi :10.1146/knowable-082422-1 . Получено 23 сентября 2022 г. .
11. Кин, Скотт Т.; Лубрано, Клаудия; Каземзаде, Сетаре; Мелианас, Армантас; Тухман, Яаков; Полино, Джузеппина; Сконьямильо, Паола; Сина, Лусио; Саллео, Альберто; ван де Бургт, Йори; Санторо, Франческа (сентябрь 2020 г.). «Бигибридный синапс с пластичностью, опосредованной нейротрансмиттерами». Природные материалы . 19 (9): 969–973. Бибкод : 2020NatMa..19..969K. дои : 10.1038/s41563-020-0703-y. ISSN  1476-4660. PMID  32541935. S2CID  219691307.
    • Пресс-релиз университета: «Исследователи разрабатывают искусственный синапс, работающий с живыми клетками». Стэнфордский университет через medicalxpress.com . Получено 23 сентября 2022 г.
12. "Искусственный нейрон обменивается дофамином с клетками мозга крысы, как настоящий". New Scientist . Получено 16 сентября 2022 г.
13. Ван, Тинг; Ван, Мин; Ван, Цзяньу; Ян, Ле; Рен, Сюэян; Песня, Банда; Чен, Шишэн; Юань, Юэхуэй; Лю, Жуйцин; Пан, Лян; Ли, Чжэн; Леу, Ван Ру; Ло, Ифэй; Цзи, Шаобо; Куи, Зекун; Он, Ке; Чжан, Фейлун; Лев, Фэнтин; Тянь, Юаньюань; Кай, Кайю; Ян, Боуэн; Ню, Цзинъи; Цзоу, Хаочэнь; Лю, Сонгруй; Сюй, Голян; Фань, Син; Ху, Бэньхуэй; Ло, Сиань Цзюнь; Ван, Ляньхуэй; Чен, Сяодун (8 августа 2022 г.). «Химически опосредованный искусственный нейрон» . Природная электроника . 5 (9): 586–595. doi : 10.1038/s41928-022-00803-0. hdl : 10356/163240 . ISSN  2520-1131. S2CID  251464760.
14. «Ученые создают крошечные устройства, которые работают как человеческий мозг». The Independent . 20 апреля 2020 г. Архивировано из оригинала 24 апреля 2020 г. Получено 17 мая 2020 г.
15. "Исследователи представили электронику, которая имитирует человеческий мозг в эффективном обучении". phys.org . Архивировано из оригинала 28 мая 2020 г. . Получено 17 мая 2020 г. .
16. Фу, Тианда; Лю, Сяомэн; Гао, Хунъянь; Уорд, Джой Э.; Лю, Сяорун; Инь, Бин; Ван, Чжунжуй; Чжо, Е; Уокер, Дэвид Дж. Ф.; Джошуа Янг, Дж.; Чен, Цзяньхан; Ловли, Дерек Р.; Яо, Цзюнь (20 апреля 2020 г.). «Биоинспирированные мемристоры бионапряжения». Природные коммуникации . 11 (1): 1861. Бибкод : 2020NatCo..11.1861F. дои : 10.1038/s41467-020-15759-y . ПМК 7171104 . ПМИД  32313096. 
17. Болахе, Саугат. «Робот Lego с органическим «мозгом» учится ориентироваться в лабиринте». Scientific American . Получено 1 февраля 2022 г.
18. Краухаузен, Имке; Куцурас, Димитриос А.; Мелианас, Армантас; Кин, Скотт Т.; Либерт, Катарина; Ледансер, Адриен; Шиламантула, Раджендар; Джованнитти, Александр; Торричелли, Фабрицио; Маккаллох, Иэн; Блом, Пол ВМ; Саллео, Альберто; Бургт, Йори ван де; Гкупиденис, Пасхалис (декабрь 2021 г.). «Органическая нейроморфная электроника для сенсомоторной интеграции и обучения робототехнике». Достижения науки . 7 (50): eabl5068. Бибкод : 2021SciA....7.5068K. doi : 10.1126/sciadv.abl5068. hdl : 10754/673986. PMC 8664264. PMID  34890232. S2CID  245046482 . 
19. Саркар, Танмой; Либерт, Катарина; Павлу, Аристея; Фрэнк, Томас; Майлендер, Волкер; Маккалок, Иэн; Блом, Пол ВМ; Торричелли, Фабрицио; Гкупиденис, Пасхалис (7 ноября 2022 г.). «Органический искусственный импульсный нейрон для нейроморфного зондирования in situ и биоинтерфейса». Природная электроника . 5 (11): 774–783. дои : 10.1038/s41928-022-00859-y . hdl : 10754/686016 . ISSN  2520-1131. S2CID  253413801.
20. «Искусственные нейроны эмулируют биологические аналоги, обеспечивая синергетическую работу». Nature Electronics . 5 (11): 721–722. 10 ноября 2022 г. doi :10.1038/s41928-022-00862-3. ISSN  2520-1131. S2CID  253469402.
21. Мартин Энтони (январь 2001 г.). Дискретная математика нейронных сетей: избранные темы. SIAM. стр. 3–. ISBN 978-0-89871-480-7.
22. Чару С. Аггарвал (25 июля 2014 г.). Классификация данных: алгоритмы и приложения. CRC Press. стр. 209–. ISBN 978-1-4665-8674-1.
23. Пол Вербос , За пределами регрессии: Новые инструменты для прогнозирования и анализа в поведенческих науках. Кандидатская диссертация, Гарвардский университет, 1974
24. Werbos, PJ (1990). «Обратное распространение ошибки во времени: что оно делает и как это делать». Труды IEEE . 78 (10): 1550–1560. doi :10.1109/5.58337. ISSN  0018-9219. S2CID  18470994.
25. Ханлозер, Ричард Х. Р.; Сарпешкар, Рахул; Маховальд, Миша А.; Дуглас, Родни Дж.; Сын, Х. Себастьян (2000). «Цифровой отбор и аналоговое усиление сосуществуют в кремниевой схеме, вдохновленной корой головного мозга». Nature . 405 (6789): 947–951. Bibcode :2000Natur.405..947H. doi :10.1038/35016072. ISSN  0028-0836. PMID  10879535. S2CID  4399014.
26. R Hahnloser; HS Seung (2001). Разрешенные и запрещенные наборы в симметричных порогово-линейных сетях . NIPS 2001.
27. Ксавье Глорот; Антуан Бордес; Йошуа Бенжио (2011). Глубокие разреженные выпрямительные нейронные сети (PDF) . AISTATS.
28. Ян ЛеКун ; Леон Ботту ; Женевьева Б. Орр; Клаус-Роберт Мюллер (1998). "Efficient BackProp" (PDF) . В G. Orr; K. Müller (ред.). Neural Networks: Tricks of the Trade . Springer.
29. Эндрю Л. Маас, Авни Й. Ханнун, Эндрю Й. Нг (2014). Нелинейности выпрямителя улучшают акустические модели нейронных сетей.

Дальнейшее чтение

• Маккалок, Уоррен С .; Питтс, Уолтер (1943). «Логическое исчисление идей, имманентных нервной деятельности». Бюллетень математической биофизики . 5 (4): 115–133. doi :10.1007/bf02478259.
• Самардак, А.; Ногарет, А.; Янсон, Н.Б.; Баланов, АГ; Фаррер, И.; Ритчи, ДА (2009-06-05). "Управляемая шумом передача сигнала в многопоточном полупроводниковом нейроне". Physical Review Letters . 102 (22): 226802. Bibcode : 2009PhRvL.102v6802S. doi : 10.1103/physrevlett.102.226802. PMID  19658886. S2CID  11211062.

Внешние ссылки

• Искусственный нейрон имитирует функцию человеческих клеток
• Нейроны Маккалока-Питтса (обзор)