слоение

В математике — разновидность отношения эквивалентности на n-многообразии.

Двумерное сечение слоения Риба

Трехмерная модель слоения Риба

В математике ( дифференциальная геометрия ) слоение — это отношение эквивалентности на n -многообразии , причем классы эквивалентности связаны, инъективно погруженные подмногообразия , все одной и той же размерности p , смоделированные на основе разложения реального координатного пространства R ⁿ на смежные классы . x + R ^p стандартно вложенного подпространства R ^p . Классы эквивалентности называются слоями слоения. ^[1] Если требуется, чтобы многообразие и/или подмногообразия имели кусочно-линейную , дифференцируемую (класса C ^r ) или аналитическую структуру, то определяют кусочно-линейное, дифференцируемое или аналитическое слоение соответственно. В наиболее важном случае дифференцируемого слоения класса Cr обычно понимают, что ^r ≥ 1 (иначе C0 ^— топологическое слоение). ^[2] Число p (размерность листьев) называется размерностью слоения, а q = n − p называется его коразмерностью .

В некоторых статьях физиков-математиков по общей теории относительности термин слоение (или нарезка ) используется для описания ситуации, когда соответствующее многообразие Лоренца (( p +1)-мерное пространство-время ) было разложено на гиперповерхности размерности p , заданные как множества уровня вещественной гладкой функции ( скалярного поля ), градиент которой всюду отличен от нуля; кроме того, эта гладкая функция обычно считается функцией времени, а это означает, что ее градиент везде подобен времени , так что все ее множества уровней являются пространственноподобными гиперповерхностями. Из уважения к стандартной математической терминологии эти гиперповерхности часто называют листьями (или иногда срезами ) слоения. ^[3] Обратите внимание, что хотя эта ситуация действительно представляет собой слоение коразмерности 1 в стандартном математическом смысле, примеры этого типа на самом деле глобально тривиальны; хотя листья (математического) слоения коразмерности 1 всегда локально являются множествами уровня функции, они, как правило, не могут быть выражены таким образом глобально, ^{[4] [5]} , поскольку лист может проходить через локально тривиализирующую карту бесконечное число раз. раз, и голономия вокруг листа может также препятствовать существованию глобально согласованных определяющих функций для листьев. Например, хотя 3-сфера имеет знаменитое слоение коразмерности 1, открытое Рибом, слоение коразмерности 1 замкнутого многообразия не может быть задано множествами уровня гладкой функции, поскольку гладкая функция на замкнутом многообразии обязательно имеет критические точки в его максимумах и минимумах.

Листованные диаграммы и атласы

Чтобы дать более точное определение слоения, необходимо определить некоторые вспомогательные элементы.

Трехмерная многослойная диаграмма с n = 3 и q = 1. Таблички двухмерные, а трансверсали одномерные.

Прямоугольная окрестность в R ⁿ — это открытое подмножество вида B = J ₁ × ⋅⋅⋅ × J _n , где J i _— (возможно, неограниченный) относительно открытый интервал на i- й координатной оси. Если J ₁ имеет вид ( a ,0), говорят, что B имеет границу ^[6]

${\displaystyle \partial B=\left\{\left(0,x^{2},\ldots ,x^{n}\right)\in B\right\}.}$

В следующем определении рассматриваются координатные карты, имеющие значения в R ^p × R ^q , что допускает возможность создания многообразий с граничными и ( выпуклыми ) углами.

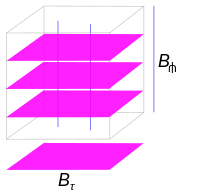
Расслоенная карта на n -многообразии M коразмерности q — это пара ( U , φ ), где ^U ⊆ M открыта и является диффеоморфизмом , являющимся прямоугольной окрестностью в Rq и прямоугольной окрестностью ^в Rp . Множество P _y = φ ⁻¹ ( B _τ × { y }), где , называется бляшкой этой слоеной карты. Для каждого x ∈ B _τ множество S _x = φ ⁻¹ ({ x } × ) называется трансверсалью слоеной карты. Множество ∂ _τ U = φ ⁻¹ ( B _τ × ( ∂ )) называется касательной границей U , а = φ ⁻¹ (( ∂B _τ ) × ) называется поперечной границей U . ^[7] ${\displaystyle \varphi :U\to B_{\tau }\times B_{\pitchfork }}$ ${\displaystyle B_{\pitchfork }}$ ${\displaystyle B_{\tau }}$ ${\displaystyle y\in B_{\pitchfork }}$ ${\displaystyle B_{\pitchfork }}$ ${\displaystyle B_{\pitchfork }}$ ${\displaystyle \partial _{\pitchfork }U}$ ${\displaystyle B_{\pitchfork }}$

Листованная диаграмма является базовой моделью для всех слоений, где пластинки представляют собой листья. Обозначение B _τ читается как « B -тангенциальный» и как « B -поперечный». Существуют также различные возможности. Если оба и B _τ имеют пустую границу, слоеная карта моделирует слоения коразмерности q n -многообразий без границы. Если одна, но не обе из этих прямоугольных окрестностей имеет границу, слоеная карта моделирует различные возможности слоений n -многообразий с краем и без углов. В частности, если ∂ ≠ ∅ = ∂B _τ , то ∂U = ∂ _τ U — объединение бляшек и слоение на бляшки касается границы. Если ∂B _τ ≠ ∅ = ∂ , то ∂U = — объединение трансверсалей и слоение трансверсально границе. Наконец, если ∂ ≠ ∅ ≠ ∂B _τ , это модель слоеного многообразия с углом, отделяющим касательную границу от поперечной границы. ^[7] ${\displaystyle B_{\pitchfork }}$ ${\displaystyle B_{\pitchfork }}$ ${\displaystyle B_{\pitchfork }}$ ${\displaystyle B_{\pitchfork }}$ ${\displaystyle \partial _{\pitchfork }U}$ ${\displaystyle B_{\pitchfork }}$

( а ) Слоение, касательное границы ∂ ≠ ∅ = ∂B _τ ; ( б ) Слоение, трансверсальное границе ∂B _τ ≠ ∅ = ∂ ; ( в ) Слоение с углом, отделяющим касательную границу от поперечной границы ∂ ≠ ∅ ≠ ∂B _τ . ${\displaystyle B_{\pitchfork }}$ ${\displaystyle B_{\pitchfork }}$ ${\displaystyle B_{\pitchfork }}$

Расслоенный атлас коразмерности q и класса C ^r (0 ≤ r ≤ ∞) на n -многообразии M — это C ^r -атлас слоеных карт коразмерности q , которые когерентно расслоены в том смысле, что всякий раз, когда P и Q являются бляшками в различных картах , то P ∩ Q открыто как в P , так и в Q . ^[8] ${\displaystyle {\mathcal {U}}=\{(U_{\alpha },\varphi _{\alpha })\mid \alpha \in A\}}$ ${\displaystyle {\mathcal {U}}}$

Полезный способ переформулировать понятие когерентно расслоенных карт — написать для w ∈ U _α ∩ U _β ^[9]

${\displaystyle \varphi _{\alpha }(w)=\left(x_{\alpha }(w),y_{\alpha }(w)\right)\in B_{\tau }^{\alpha }\times B_{\pitchfork }^{\alpha },}$

${\displaystyle \varphi _{\beta }(w)=\left(x_{\beta }(w),y_{\beta }(w)\right)\in B_{\tau }^{\beta }\times B_{\pitchfork }^{\beta }.}$

Обозначение ( U _α , φ _α ) часто пишется ( U _α , x _α , y _α ), с ^[9]

${\displaystyle x_{\alpha }=\left(x_{\alpha }^{1},\dots ,x_{\alpha }^{p}\right),}$

${\displaystyle y_{\alpha }=\left(y_{\alpha }^{1},\dots ,y_{\alpha }^{q}\right).}$

На φ _β ( U _α ∩ U _β ) формулу координат можно изменить как ^[9]

${\displaystyle g_{\alpha \beta }\left(x_{\beta },y_{\beta }\right)=\varphi _{\alpha }\circ \varphi _{\beta }^{-1}\left(x_{\beta },y_{\beta }\right)=\left(x_{\alpha }\left(x_{\beta },y_{\beta }\right),y_{\alpha }\left(x_{\beta },y_{\beta }\right)\right).}$

Каждая бляшка U _α встречается с двумя бляшками U _β .

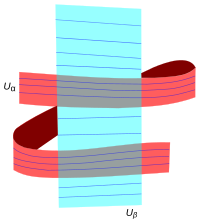
Условие когерентного расслоения ( U _α , x _α , y _α ) и ( U _β , x _β , y _β ) означает, что, если P ⊂ U _α — бляшка, компоненты связности P ∩ U _β лежат в ( возможно отдельные) бляшки U _β . Эквивалентно, поскольку пластинки U _α и U _β являются множествами уровня поперечных координат y _α и y _β соответственно, каждая точка z ∈ U _α ∩ U _β имеет окрестность, в которой справедлива формула

${\displaystyle y_{\alpha }=y_{\alpha }(x_{\beta },y_{\beta })=y_{\alpha }(y_{\beta })}$

не зависит от x _β . ^[9]

Основное назначение листоватых атласов — соединение их перекрывающихся бляшек с образованием листьев слоения. Для этой и других целей общее определение листоватого атласа, приведенное выше, немного неуклюже. Одна из проблем заключается в том, что пластинка ( U _α , φ _α ) может встречаться с несколькими пластинками ( U _β , φ _β ). Может даже случиться так, что табличка одной карты встретится с бесконечным множеством пластинок другой карты. Однако не теряется общность, если предположить, что ситуация гораздо более регулярна, как показано ниже.

Два расслоенных атласа и на M одной и той же коразмерности и класса гладкости C ^r когерентны, если – расслоенный C ^r -атлас. Связность расслоенных атласов является отношением эквивалентности. ^[9] ${\displaystyle {\mathcal {U}}}$ ${\displaystyle {\mathcal {V}}}$ ${\displaystyle \left({\mathcal {U}}\thickapprox {\mathcal {V}}\right)}$ ${\displaystyle {\mathcal {U}}\cup {\mathcal {V}}}$

Примеры диаграмм в обычном листовом атласе.

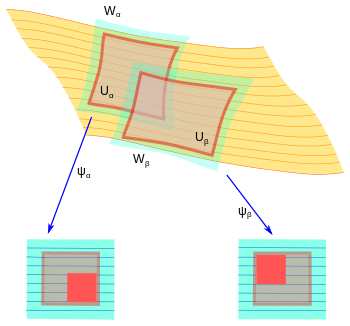
Таблички и трансверсали, определенные выше на открытых наборах, также являются открытыми. Но можно говорить и о закрытых бляшках и трансверсалах. А именно, если ( U , φ ) и ( W , ψ ) — расслоенные карты такие, что ( замыкание U ) является подмножеством W и φ = ψ | U тогда, если можно увидеть , что записанное диффеоморфно переносится на ${\displaystyle {\overline {U}}}$ ${\displaystyle \varphi (U)=B_{\tau }\times B_{\pitchfork },}$ ${\displaystyle \psi |{\overline {U}}}$ ${\displaystyle {\overline {\varphi }}}$ ${\displaystyle {\overline {U}}}$ ${\displaystyle {\overline {B}}_{\tau }\times {\overline {B}}_{\pitchfork }.}$

Расслоенный атлас называется правильным , если

1. для каждого α ∈ A является компактным подмножеством слоеной карты ( W _α , ψ _α ) и φ _α = ψ _α | У _α ; ${\displaystyle {\overline {U}}_{\alpha }}$
2. покрытие { U _α | _ α ∈ A } локально конечен ;
3. если ( U _α , φ _α ) и ( U _β , φ _β ) — элементы слоеного атласа, то внутренность каждой замкнутой бляшки P ⊂ встречается не более чем с одной бляшкой в ^​​[11] ${\displaystyle {\overline {U}}_{\alpha }}$ ${\displaystyle {\overline {U}}_{\beta }.}$

По свойству (1) координаты x _α и y _α распространяются на координаты и on , и записывают Свойство (3) эквивалентно требованию, чтобы, если U _α ∩ U _β ≠ ∅, изменения поперечных координат не зависели от ${\displaystyle {\overline {x}}_{\alpha }}$ ${\displaystyle {\overline {y}}_{\alpha }}$ ${\displaystyle {\overline {U}}_{\alpha }}$ ${\displaystyle {\overline {\varphi }}_{\alpha }=\left({\overline {x}}_{\alpha },{\overline {y}}_{\alpha }\right).}$ ${\displaystyle {\overline {y}}_{\alpha }={\overline {y}}_{\alpha }\left({\overline {x}}_{\beta },{\overline {y}}_{\beta }\right)}$ ${\displaystyle {\overline {x}}_{\beta }.}$

${\displaystyle {\overline {g}}_{\alpha \beta }={\overline {\varphi }}_{\alpha }\circ {\overline {\varphi }}_{\beta }^{-1}:{\overline {\varphi }}_{\beta }\left({\overline {U}}_{\alpha }\cap {\overline {U}}_{\beta }\right)\rightarrow {\overline {\varphi }}_{\alpha }\left({\overline {U}}_{\alpha }\cap {\overline {U}}_{\beta }\right)}$

имеет формулу ^[11]

${\displaystyle {\overline {g}}_{\alpha \beta }\left({\overline {x}}_{\beta },{\overline {y}}_{\beta }\right)=\left({\overline {x}}_{\alpha }\left({\overline {x}}_{\beta },{\overline {y}}_{\beta }\right),{\overline {y}}_{\alpha }\left({\overline {y}}_{\beta }\right)\right).}$

Аналогичные утверждения справедливы и для открытых карт (без надчерков). Отображение поперечных координат y _α можно рассматривать как погружение

${\displaystyle y_{\alpha }:U_{\alpha }\rightarrow \mathbb {R} ^{q}}$

а формулы y _α = y _α ( y _β ) можно рассматривать как диффеоморфизмы

${\displaystyle \gamma _{\alpha \beta }:y_{\beta }\left(U_{\alpha }\cap U_{\beta }\right)\rightarrow y_{\alpha }\left(U_{\alpha }\cap U_{\beta }\right).}$

Они удовлетворяют условиям коцикла . То есть на y _δ ( U _α ∩ U _β ∩ U _δ ),

${\displaystyle \gamma _{\alpha \delta }=\gamma _{\alpha \beta }\circ \gamma _{\beta \delta }}$

и, в частности, ^[12]

${\displaystyle \gamma _{\alpha \alpha }\equiv y_{\alpha }\left(U_{\alpha }\right),}$

${\displaystyle \gamma _{\alpha \beta }=\gamma _{\beta \alpha }^{-1}.}$

Используя приведенные выше определения связности и регулярности, можно доказать, что каждый слоеный атлас имеет регулярное последовательное уточнение . ^[13]

Определения слоений

Существует несколько альтернативных определений слоения в зависимости от способа достижения слоения. Самый распространенный способ достижения слоения - это разложение, достигающее следующих

Разложение по функции координат x  : U → R ⁿ .

Определение. p -мерное слоение класса C ^r n -мерного многообразия M представляет собой разложение M в объединение непересекающихся связных подмногообразий { L _α } _{αε A} , называемых слоями слоения, со следующим свойством: каждая точка в M имеет окрестность U и систему локальных координат класса C ^r x =( x ¹ , ⋅⋅⋅, x ⁿ ) : U → R ⁿ такие, что для каждого листа L _α компоненты U ∩ L _α равны описывается уравнениями x ^{p +1} =константа, ⋅⋅⋅, x ⁿ =константа. Слоение обозначается ={ L _α } _{αا A} . ^[5] ${\displaystyle {\mathcal {F}}}$

Понятие листьев позволяет интуитивно думать о слоении. Для немного более геометрического определения p -мерное слоение n -многообразия M можно рассматривать как просто набор { M _a } попарно непересекающихся, связных, погруженных p -мерных подмногообразий (листов слоения) M , такая, что для каждой точки x в M существует карта с U , гомеоморфная Rn , содержащая x, такая, что каждый лист M ^a встречается с U либо в пустом множестве, либо в счетном наборе подпространств, образы которых под in _равны p - размерные аффинные подпространства , первые n - p координаты которых постоянны. ${\displaystyle {\mathcal {F}}}$ ${\displaystyle (U,\varphi )}$ ${\displaystyle \varphi }$ ${\displaystyle \varphi (M_{a}\cap U)}$

Локально каждое слоение является погружением , допускающим следующие

Определение. Пусть M и Q — многообразия размерности n и q ≤ n соответственно, и пусть f  : M → Q — субмерсия, то есть предположим, что ранг дифференциала функции (якобиана ) равен q . Из теоремы о неявной функции следует , что ƒ индуцирует слоение коразмерности q на M , где листья определяются как компоненты f ⁻¹ ( x ) для x ∈ Q . ^[5]

Это определение описывает слоение размерности - p n -мерного многообразия M , которое покрыто картами U _i вместе с отображениями ${\displaystyle {\mathcal {F}}}$

${\displaystyle \varphi _{i}:U_{i}\to \mathbb {R} ^{n}}$

такие, что для перекрывающихся пар U _i , U _j функции перехода φ _ij  : Rn → Rn ^{, определяемые} формулой

${\displaystyle \varphi _{ij}=\varphi _{j}\varphi _{i}^{-1}}$

принять форму

${\displaystyle \varphi _{ij}(x,y)=(\varphi _{ij}^{1}(x),\varphi _{ij}^{2}(x,y))}$

где x обозначает первые координаты q = n - p , а y обозначает последние p координаты. То есть,

${\displaystyle {\begin{aligned}\varphi _{ij}^{1}:{}&\mathbb {R} ^{q}\to \mathbb {R} ^{q}\\\varphi _{ij}^{2}:{}&\mathbb {R} ^{n}\to \mathbb {R} ^{p}\end{aligned}}}$

Расщепление функций перехода φ _ij на и в составе погружения полностью аналогично расщеплению на и в составе определения регулярного слоеного атласа. Это делает возможным другое определение слоений в терминах правильных расслоенных атласов. Для этого нужно сначала доказать, что каждому регулярному слоеному атласу коразмерности q соответствует единственное слоение коразмерности q . ^[13] ${\displaystyle \varphi _{ij}^{1}(x)}$ ${\displaystyle \varphi _{ij}^{2}(x,y)}$ ${\displaystyle {\overline {g}}_{\alpha \beta }}$ ${\displaystyle {\overline {y}}_{\alpha }\left({\overline {y}}_{\beta }\right)}$ ${\displaystyle {\overline {x}}_{\alpha }\left({\overline {x}}_{\beta },{\overline {y}}_{\beta }\right)}$ ${\displaystyle {\mathcal {F}}}$

Как показано в доказательстве, слои слоения представляют собой классы эквивалентности цепочек пластинок длины ≤ p , которые также являются топологически погруженными хаусдорфовыми p -мерными подмногообразиями . Далее показано, что отношение эквивалентности бляшек на листе выражается в эквивалентности связных расслоенных атласов по отношению к их ассоциации со слоением. Более конкретно, если и являются расслоенными атласами на M и если ассоциирован со слоением, то и когерентны тогда и только тогда, когда также ассоциирован с . ^[10] ${\displaystyle {\mathcal {U}}}$ ${\displaystyle {\mathcal {V}}}$ ${\displaystyle {\mathcal {U}}}$ ${\displaystyle {\mathcal {F}}}$ ${\displaystyle {\mathcal {U}}}$ ${\displaystyle {\mathcal {V}}}$ ${\displaystyle {\mathcal {V}}}$ ${\displaystyle {\mathcal {F}}}$

Теперь очевидно, что соответствие между слоениями на M и связанными с ними слоенными атласами индуцирует взаимно однозначное соответствие между множеством слоений на M и множеством классов связности слоеных атласов или, другими словами, слоением коразмерности q и класс C ^r на M — класс связности расслоенных атласов коразмерности q и класса C ^r на M . ^[14] По лемме Цорна очевидно, что каждый класс когерентности расслоенных атласов содержит единственный максимальный расслоенный атлас. Таким образом, ${\displaystyle {\mathcal {F}}}$

Определение. Слоением коразмерности q и класса C ^r на M называется максимальный расслоенный C ^r -атлас коразмерности q на M . ^[14]

На практике для представления слоения обычно используется относительно небольшой листоватый атлас. Обычно также требуется, чтобы этот атлас был регулярным.

На диаграмме U _i полосы x = константа совпадают с полосами на других диаграммах U _j . Эти подмногообразия соединяются от карты к карте, образуя максимальные связные инъективно погруженные подмногообразия , называемые листьями слоения.

Если сжать карту U _i , ее можно записать как U _ix × U _iy , где U _ix ⊂ R ^{n − p} , U _iy ⊂ R ^p , U _iy гомеоморфен бляшкам, а точки U _ix параметризуют бляшки в У _я . Если выбрать y ₀ в U _iy , то U _ix × { y ₀ } является подмногообразием U _i , которое пересекает каждую пластинку ровно один раз. Это называется локальным поперечным сечением слоения. Заметим, что из-за монодромии глобальные трансверсальные сечения слоения могут не существовать.

Случай r = 0 весьма особенный. Те слоения С ⁰ , которые возникают на практике, обычно являются «гладколистными». Точнее, они принадлежат классу C ^{r ,0} в следующем смысле.

Определение. Слоение имеет класс C ^r,k , r > k ≥ 0, если соответствующий класс когерентности расслоенных атласов содержит правильный расслоенный атлас { U _α , x _α , y _α } _{αε A} такой, что формула замены координат ${\displaystyle {\mathcal {F}}}$

${\displaystyle g_{\alpha \beta }(x_{\beta },y_{\beta })=(x_{\alpha }(x_{\beta },y_{\beta }),y_{\alpha }(y_{\beta })).}$

имеет класс C ^k , но x _α принадлежит классу C ^r в координатах x _β и его смешанные частичные части x _β порядков ≤  r представляют собой C ^k в координатах ( x _β , y _β ). ^[14]

Приведенное выше определение предполагает более общую концепцию расслоенного пространства или абстрактной ламинации . Ослабляют условие, что трансверсали являются открытыми, относительно компактными подмножествами R ^q , позволяя трансверсальным координатам y _α принимать свои значения в некотором более общем топологическом пространстве Z . Бляшки по-прежнему являются открытыми, относительно компактными подмножествами R ^p , замена формулы поперечной координаты y _α ( y _β ) непрерывна и x _α ( x _β , y _β ) имеет класс C ^r в координатах x _β и ее смешанную Части x _β порядков ≤  r непрерывны в координатах ( x _β , y _β ). Обычно требуется, чтобы M и Z были локально компактными, счетными и метризуемыми. Это может показаться довольно диким обобщением, но есть контексты, в которых оно полезно. ^[15]

Голономия

Пусть ( M , ) — слоеное многообразие. Если L — лист и s — путь в L , нас интересует поведение слоения в окрестности s в M. Интуитивно житель листа идет по тропинке s , наблюдая за всеми близлежащими листьями. По мере их продвижения (далее обозначаемого s ( t )) некоторые из этих листьев могут «отслаиваться», выходя за пределы поля зрения, другие могут внезапно войти в зону действия и асимптотически приблизиться к L , другие могут следовать за ними более или менее параллельно. мода или обмотать L сбоку и т. д . Если s является петлей, то s ( t ) неоднократно возвращается в одну и ту же точку s ( t ₀ ), поскольку t стремится к бесконечности, и каждый раз все больше и больше листьев могут попасть в поле зрения или исчезнуть из поля зрения и т. д . Такое поведение, если оно соответствующим образом формализовано, называется голономией слоения . ${\displaystyle {\mathcal {F}}}$ ${\displaystyle {\mathcal {F}}}$

Голономия реализуется на расслоенных многообразиях различными конкретными способами: группа полной голономии расслоенных расслоений, псевдогруппа голономии общих расслоенных многообразий, зародышевый группоид голономии общих расслоенных многообразий, зародышевая группа голономии листа и инфинитезимальная группа голономии лист.

Листистые пучки

Самый простой для понимания случай голономии — это полная голономия расслоенного пучка. Это обобщение понятия отображения Пуанкаре .

Сечение N и первое отображение возврата f , где M = S ¹ × D ² и N = D ² .

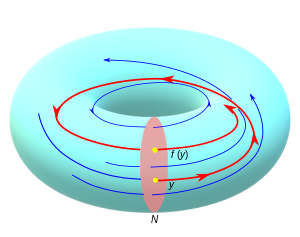
Термин «отображение первого возврата (рекуррентности)» пришел из теории динамических систем. Пусть Φ _t — неособый поток C ^r ( r  ≥ 1) на компактном n -многообразии M . В приложениях можно представить, что М — это циклотрон или какой-нибудь замкнутый контур с потоком жидкости. Если M имеет границу, предполагается, что поток касается границы. Поток порождает одномерное слоение . Если помнить о положительном направлении потока, но забывать о параметризации (форме траектории, скорости и т. д .), лежащее в основе слоение называется ориентированным. Предположим , что поток имеет глобальное сечение N. То есть N — компактное, правильно вложенное ^{подмногообразие} Cr в M размерности n –  1, слоение трансверсально N , и каждая линия потока пересекает N. Поскольку размеры N и листьев дополняют друг друга, условие трансверсальности состоит в том, что ${\displaystyle {\mathcal {F}}}$ ${\displaystyle {\mathcal {F}}}$ ${\displaystyle {\mathcal {F}}}$

${\displaystyle T_{y}(M)=T_{y}({\mathcal {F}})\oplus T_{y}(N){\text{ for each }}y\in N.}$

Пусть y ∈ N и рассмотрим ω - предельное множество ω( y ) всех точек накопления в M всех последовательностей , где t _k стремится к бесконечности. Можно показать, что ω(y) компактна, непуста и представляет собой объединение линий тока. Если существует значение t * ∈ R такое, что Φ _{t *} ( z ) ∈ N , и отсюда следует, что ${\displaystyle \left\{\Phi _{t_{k}}(y)\right\}_{k=1}^{\infty }}$ ${\displaystyle z=\lim _{k\rightarrow \infty }\Phi _{t_{k}}\in \omega (y),}$

${\displaystyle \lim _{k\to \infty }\Phi _{t_{k}+t^{\ast }}(y)=\Phi _{t^{\ast }}(z)\in N.}$

Поскольку N компактно и трансверсально к N , отсюда следует, что множество { t > 0 | Φ _t ( y ) ∈ N} — монотонно возрастающая последовательность , расходящаяся до бесконечности. ${\displaystyle {\mathcal {F}}}$ ${\displaystyle \{\tau _{k}(y)\}_{k=1}^{\infty }}$

Поскольку y ∈ N меняется, пусть τ ( y ) = τ ₁ ( y ), определяя таким образом положительную функцию τ ∈ C ^r ( N ​​) (время первого возврата) такую, что для произвольного y ∈ N Φ _t ( y ) ∉ N , 0 < т < τ ( y ) и Φ _{τ ( y )} ( y ) ∈ N .

Определим f  : N → N по формуле f ( y ) = Φ _{τ ( y )} ( y ). Это ^карта Cr . Если поток обратный, точно такая же конструкция дает обратное f ⁻¹ ; поэтому f ∈ Diff ^r ( N ​​). Этот диффеоморфизм является первым отображением возврата, а τ называется временем первого возврата . Хотя время первого возврата зависит от параметризации потока, должно быть очевидно, что f зависит только от ориентированного слоения . Поток Φ _t можно перепараметризовать , сохранив его неособым, класса C ^r и не меняя его направления, так что  τ  ≡ 1. ${\displaystyle {\mathcal {F}}}$

Предположение о том, что поток имеет поперечное сечение N, является очень ограничительным, подразумевая, что M — это полное пространство расслоения над S ¹ . Действительно, на R × N определим ~ _f как отношение эквивалентности, порожденное

${\displaystyle (t,y)\sim _{f}(t-1,f(y)).}$

Эквивалентно, это орбитальная эквивалентность действия аддитивной группы Z на R × N , определяемая формулой

${\displaystyle k\cdot (t,y)=(t-k,f^{k}(y)),}$

для каждого k ∈ Z и для каждого ( t , y ) ∈ R × N. Цилиндр отображения f определяется как Cr ^- многообразие

${\displaystyle M_{f}=(\mathbb {R} \times N)/{\sim _{f}}.}$

Согласно определению первого отображения возврата f и предположению, что время первого возврата равно τ ≡ 1, сразу видно, что отображение

${\displaystyle \Phi :\mathbb {R} \times N\rightarrow M.}$

определенный потоком, индуцирует канонический диффеоморфизм C ^r

${\displaystyle \varphi :M_{f}\rightarrow M.}$

Если мы отождествим M _f = M , то проекция R × N на R индуцирует отображение C ^r

${\displaystyle \pi :M\rightarrow \mathbb {R} /\mathbb {Z} =S^{1}}$

это превращает M в полное пространство расслоения над кругом. Это ^просто проекция S1 × D2 на S1 ^{. _} Слоение трансверсально слоям этого расслоения, а проекция расслоения  π , ограниченная на каждый слой ^L , является накрывающим отображением π  : L → S1 . Это называется расслоенным пучком . ${\displaystyle {\mathcal {F}}}$

В качестве базовой точки x ₀ ∈ S ¹ возьмем класс эквивалентности 0 + Z ; поэтому π ⁻¹ ( x ₀ ) — исходное сечение N. Для каждой петли s на S1 ^, базирующейся в точке x0 , гомотопический класс [ _s ] ∈ π1 ₍ S1 , x0 ⁾ однозначно характеризуется deg s _∈ Z. Петля s поднимается до пути в каждой линии потока, и должно быть ясно, что подъем s _y , который начинается в точке y ∈ N , заканчивается в ^{точке fk} ( y ) ∈ N , где k = deg s . Диффеоморфизм f ^k ∈ Diff ^r ( N ) также обозначается h _s и называется полной голономией петли s . Поскольку это зависит только от [ s ], это определение гомоморфизма

${\displaystyle h:\pi _{1}(S^{1},x_{0})\rightarrow \operatorname {Diff} ^{\,r}(N),}$

называется гомоморфизмом полной голономии расслоения.

Используя расслоения более прямым способом, пусть ( M , ) — расслоенное n -многообразие коразмерности q . Пусть π  : M → B — расслоение с q - мерным слоем F и связным базовым пространством B. Предположим, что все эти структуры относятся к классу C ^r , 0 ⩽ r ⩽ ∞, с условием, что, если r = 0, B поддерживает структуру C ¹ . Поскольку каждый максимальный атлас C ^{1 на} B содержит податлас C ^∞ , общность не теряется, если предположить, что B желаемой гладкости. Наконец, предположим, что для каждого x ∈ B существует связная открытая окрестность U ⊆ B точки x и локальная тривиализация ${\displaystyle {\mathcal {F}}}$

${\displaystyle {\begin{matrix}\pi ^{-1}(U)&{\xrightarrow {\varphi }}&U\times {F}\\\scriptstyle {\pi }{\Bigg \downarrow }&{\qquad }&{\Bigg \downarrow }{\scriptstyle {p}}\\U&{\xrightarrow {\text{id}}}&U\end{matrix}}}$

где φ — диффеоморфизм C ^r (гомеоморфизм, если r = 0), который переводит в слоение произведения { U × { y }} _{y  ∈  F} . Здесь – слоение с листьями — компоненты связности L ∩ π ⁻¹ ( U ), где L пробегает слои . Это общее определение термина «расслоенное расслоение» ( M , ,π ) класса C ^r . ${\textstyle {\mathcal {F}}\mid \pi ^{-1}(U)}$ ${\textstyle {\mathcal {F}}\mid \pi ^{-1}(U)}$ ${\displaystyle {\mathcal {F}}}$ ${\displaystyle {\mathcal {F}}}$

${\displaystyle {\mathcal {F}}}$трансверсально слоям π (говорят, что трансверсально расслоению) и что ограничение π на каждый слой L является накрывающим отображением π : L → B . В частности, каждый слой F _x = π ⁻¹ ( x ) пересекает каждый лист . Волокно представляет собой поперечное сечение в полной аналогии с понятием поперечного сечения потока. ${\displaystyle {\mathcal {F}}}$ ${\displaystyle {\mathcal {F}}}$ ${\displaystyle {\mathcal {F}}}$ ${\displaystyle {\mathcal {F}}}$

Трансверсальное слоям слоение само по себе не гарантирует, что слои являются накрывающими пространствами B . Простым вариантом задачи является слоение R2 , ^{трансверсальное} расслоению ${\displaystyle {\mathcal {F}}}$

${\displaystyle \pi :\mathbb {R} ^{2}\rightarrow \mathbb {R} ,}$

${\displaystyle \pi (x,y)=x,}$

но с бесконечно большим количеством листьев, у которых отсутствует ось Y. На соответствующем рисунке подразумевается, что «помеченные стрелками» листья и все, что находятся над ними, асимптотичны оси x = 0. Такое слоение называют неполным относительно расслоения, имея в виду, что некоторые из листьев «сбегают к бесконечность», когда параметр x ∈ B приближается к некоторому x ₀ ∈ B . Точнее, могут существовать лист L и непрерывный путь s  : [0, a ) → L такие, что lim _{t → a −} π( s ( t )) = x ₀ ∈ B , но lim _{t → a −} s ( t ) не существует в топологии многообразия L. Это аналогично случаю неполных потоков, когда некоторые линии тока «уходят в бесконечность» за конечное время. Хотя такой лист L может в другом месте встречаться с π ⁻¹ ( x ₀ ), он не может равномерно покрывать окрестность x ₀ и, следовательно, не может быть накрывающим пространством B относительно π . Однако когда F компактно, верно, что трансверсальность расслоения действительно гарантирует полноту, следовательно, это расслоенное расслоение. ${\displaystyle {\mathcal {F}}}$ ${\textstyle (M,{\mathcal {F}},\pi )}$

Существует атлас = { U _α , x _α } _αεA на B , состоящий из открытых связных координатных карт вместе с тривиализациями φ _α  : π ⁻¹ ( U _α ) → U _α × F , которые несут |π ⁻¹ ( U _α ) к слоению произведения. Положим W _α = π ⁻¹ ( U _α ) и напишем φ _α = ( x _α , y _α ), где (злоупотребляя обозначениями) x _α представляет собой x _α ∘ π и y _α  : π ⁻¹ ( U _α ) → F — это погружение, полученное составлением φ _α с канонической проекцией U _α × F → F . ${\displaystyle {\mathcal {U}}}$ ${\displaystyle {\mathcal {F}}}$

Атлас = { W _α , x _α , y _α } _{α ∈ A} играет роль, аналогичную роли расслоенного атласа. Пластины Wα являются множествами уровня yα _{, и это} семейство пластинок идентично F _через yα . Поскольку предполагается, что B поддерживает структуру C ^∞ , согласно теореме Уайтхеда можно зафиксировать риманову метрику на B и выбрать атлас геодезически выпуклым. Таким образом, U _α ∩ U _β всегда связен. Если это пересечение непусто, каждая пластинка Wα соответствует _{ровно одной} пластинке Wβ . Затем определите коцикл голономии , установив ${\displaystyle {\mathcal {W}}}$ ${\displaystyle {\mathcal {U}}}$ ${\displaystyle \gamma =\left\{\gamma _{\alpha \beta }\right\}_{\alpha ,\beta \in A}}$

${\displaystyle \gamma _{\alpha \beta }=y_{\alpha }\circ y_{\beta }^{-1}:F\rightarrow F.}$

Примеры

Плоское пространство

Рассмотрим n -мерное пространство, расслоенное как произведение на подпространства, состоящие из точек, первые n - p координаты которых постоянны. Это можно охватить одной диаграммой. По сути, утверждение состоит в том, что R ⁿ = R ^{n − p} × R ^p , при этом листья или пластинки R ^p нумеруются как R ^{n − p} . Аналогию можно увидеть непосредственно в трех измерениях, если принять n = 3 и p = 2 : двумерные листы книги нумеруются (1-мерным) номером страницы.

Пакеты

Достаточно тривиальным примером слоений являются произведения M = B × F , расслоенные на листы F _b = { b } × F , b ∈ B. (Другое слоение M задается формулой B _f = B × {  f  } ,   f   ∈ F .)

Более общий класс — это плоские G -расслоения с G = Homeo( F ) для многообразия F. Учитывая представление ρ  : π ₁ ( B ) → Homeo( F ) , плоское Homeo( F ) -расслоение с монодромией ρ имеет вид , где π ₁ ( B ) действует на универсальном накрытии преобразованиями колоды и на F посредством представления ρ . ${\displaystyle M=\left({\widetilde {B}}\times F\right)/\pi _{1}B}$ ${\displaystyle {\widetilde {B}}}$

Плоские пучки укладываются в каркас пучков волокон . Отображение π  : M → B между многообразиями является расслоением, если существует многообразие F такое, что каждый b ∈ B имеет открытую окрестность U такую, что существует гомеоморфизм с , с p ₁  : U × F → U проекцией на первый фактор. Расслоение дает слоение на слои . Его пространство слоев L гомеоморфно B , в частности, L — хаусдорфово многообразие. ${\displaystyle \varphi :\pi ^{-1}(U)\to U\times F}$ ${\displaystyle \pi =p_{1}\varphi }$ ${\displaystyle F_{b}:=\pi ^{-1}(\{b\}),b\in B}$

Покрытия

Если M → N — накрывающее отображение между многообразиями, а F — слоение на N , то оно возвращается к слоению на M. В более общем смысле, если карта представляет собой просто разветвленное покрытие , где место ветвления поперечно слоению, то слоение можно отодвинуть назад.

Погружения

Если M ⁿ → N ^q , ( q ≤ n ) является субмерсией многообразий, из теоремы об обратной функции следует , что компоненты связности слоев субмерсии определяют слоение коразмерности q многообразия M . Пучки волокон являются примером этого типа.

Пример погружения, не являющегося расслоением, дается выражением

${\displaystyle {\begin{cases}f:[-1,1]\times \mathbb {R} \to \mathbb {R} \\f(x,y)=(x^{2}-1)e^{y}\end{cases}}}$

Эта субмерсия дает слоение [−1, 1] × R , которое инвариантно относительно Z -действий, заданных формулой

${\displaystyle z(x,y)=(x,y+n),\quad {\text{or}}\quad z(x,y)=\left((-1)^{n}x,y\right)}$

для ( x , y ) ∈ [−1, 1] × R и n ∈ Z . Индуцированные слоения Z \ ([−1, 1] × R ) называются двумерным слоением Риба (кольца) соответственно. двумерное неориентируемое слоение Риба (ленты Мёбиуса). Их листовые пространства не Хаусдорфы.

Слоения Риба

Дайте определение погружению

${\displaystyle {\begin{cases}f:D^{n}\times \mathbb {R} \to \mathbb {R} \\f(r,\theta ,t):=(r^{2}-1)e^{t}\end{cases}}}$

где ( r , θ ) ∈ [0, 1] × S ^{n −1} — цилиндрические координаты на n -мерном диске D ⁿ . Эта субмерсия дает слоение D ⁿ × R , которое инвариантно относительно Z -действий, заданных формулой

${\displaystyle z(x,y)=(x,y+z)}$

для ( Икс , y ) ∈ D ^п × р , z ∈ Z . Индуцированное слоение Z \( ^Dn × R ) называется n - мерным слоением Риба . Его листовое пространство не является Хаусдорфом.

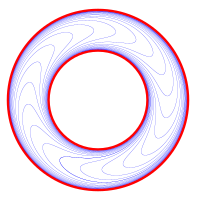
Для n = 2 это дает слоение полнотория, которое можно использовать для определения слоения Риба 3-сферы путем склеивания двух полноторий вдоль их границы. Слоения нечетномерных сфер S ^{2 n +1} также известны явно. ^[16]

Группы лжи

Если G — группа Ли , а H — подгруппа Ли , то G расслоена на смежные классы H. Когда H замкнуто в G , факторпространство G / H является гладким ( хаусдорфовым ) многообразием, превращающим G в расслоение со слоем H и базой G / H . Это расслоение фактически является главным со структурной группой H.

Групповые действия лжи

Пусть G — группа Ли , гладко действующая на многообразии M. Если действие является локально свободным действием или свободным действием , то орбиты группы G определяют слоение M.

Линейные слоения и слоения Кронекера

Если - неособое ( т . е . нигде не нулевое) векторное поле, то локальный поток, определяемый объединением фрагментов, определяет слоение размерности 1. Действительно, для произвольной точки x ∈ M тот факт, что она неособа, позволяет найти координату окрестности ( U , x ¹ ,..., x ⁿ ) вокруг x такая, что ${\displaystyle {\tilde {X}}}$ ${\displaystyle {\tilde {X}}}$ ${\displaystyle {\tilde {X}}}$

${\displaystyle -\varepsilon <x^{i}<\varepsilon ,\quad 1\leq i\leq n,}$

и

${\displaystyle {\frac {\partial }{\partial x^{1}}}={\tilde {X}}\mid U.}$

Геометрически линии тока представляют собой всего лишь наборы уровней. ${\displaystyle {\tilde {X}}\mid U}$

${\displaystyle x^{i}=c^{i},\quad 2\leq i\leq n,}$

где все многообразия по соглашению являются вторыми счетными, листовые аномалии, такие как «длинная линия», исключаются второй счетностью самого M. Эту трудность можно обойти, потребовав, чтобы поле было полным ( например , чтобы M было компактным), следовательно, чтобы каждый лист был линией потока. ${\displaystyle |c^{i}|<\varepsilon .}$ ${\displaystyle {\tilde {X}}}$

Линейное слоение на R2 ^{переходит} в слоение на T2 ^. а) наклон рациональный (линейное слоение); б) наклон иррационален (слоение Кронекера). ${\displaystyle {\mathcal {\tilde {F}}}}$ ${\displaystyle {\mathcal {F}}}$

Иррациональное вращение на 2-торе.

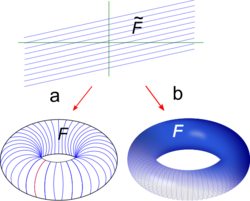
Важный класс одномерных слоений на торе T ² получается путем проектирования постоянных векторных полей на T ² . Постоянное векторное поле

${\displaystyle {\tilde {X}}\equiv {\begin{bmatrix}a\\b\end{bmatrix}}}$

на R ² инвариантно для всех сдвигов в R ² и, следовательно, переходит в четко определенное векторное поле X при проектировании на тор T ² = R ² / Z ² . Предполагается, что a ≠ 0. Слоение на R ² , образованное , имеет в качестве листьев параллельные прямые наклона θ = b / a . Это слоение также инвариантно относительно сдвигов и переходит в слоение на T ² , порожденное X . ${\displaystyle {\mathcal {\tilde {F}}}}$ ${\displaystyle {\tilde {X}}}$ ${\displaystyle {\mathcal {F}}}$

Каждый лист имеет форму ${\displaystyle {\mathcal {\tilde {F}}}}$

${\displaystyle {\tilde {L}}=\{(x_{0}+ta,y_{0}+tb)\}_{t\in \mathbb {R} }.}$

Если наклон рационален , то все листы представляют собой замкнутые кривые , гомеоморфные окружности . В этом случае можно взять a , b ∈ Z. Для фиксированного t ∈ R все точки, соответствующие значениям t ∈ t ₀ + Z , проектируются в одну и ту же точку T ² ; поэтому соответствующий лист L является вложенной окружностью в T ² . Поскольку L произвольна, является слоением T ² на окружности. Отсюда довольно легко следует, что это слоение на самом деле является расслоением π: T ² → S ¹ . Это известно как линейное слоение . ${\displaystyle {\tilde {L}}}$ ${\displaystyle {\mathcal {F}}}$ ${\displaystyle {\mathcal {F}}}$

Когда наклон θ = b / a иррационален , листья некомпактны , гомеоморфны некомпактифицированной вещественной прямой и плотны в торе (см. Иррациональное вращение ). Траектория каждой точки ( x ₀ , y ₀ ) никогда не возвращается в одну и ту же точку, а порождает «везде плотную» обмотку тора, т. е. приближается к любой заданной точке сколь угодно близко. Таким образом, замыканием траектории является весь двумерный тор. Этот случай назван слоением Кронекера в честь Леопольда Кронекера и его

Теорема Кронекера о плотности . Если действительное число θ отличается от каждого рационального числа, кратного π, то множество { e ^inθ | n ∈ Z } плотно в единичном круге.

Аналогичная конструкция с использованием слоения Rn на параллельные прямые дает 1-мерное слоение n -тора Rn ^/ Zn ^{, связанное} с линейным потоком на торе .

Подвесные слоения

Плоский расслоение имеет не только слоение на слои, но и поперечное к слоям слоение, листы которого

${\displaystyle L_{f}:=\left\{p\left({\tilde {b}},f\right):{\tilde {b}}\in {\widetilde {B}}\right\},\quad {\mbox{ for }}f\in F,}$

где каноническая проекция. Это слоение называется надстройкой представления ρ  : π ₁ ( B ) → Homeo( F ) . ${\displaystyle p:{\widetilde {B}}\times F\to M}$

В частности, если B = S ¹ и является гомеоморфизмом F , то слоение надстройки определяется как слоение надстройки представления ρ  : Z → Homeo( F ) , заданного формулой ρ ( z ) = Φ ^z . Его пространство листьев — это L = /~ , где x ~ y всякий раз, когда y = Φ ⁿ ( x ) для некоторого n ∈ Z. ${\displaystyle \varphi :F\to F}$ ${\displaystyle \varphi }$ ${\displaystyle {\mathcal {F}}}$

Простейшим примером слоения надстройкой является многообразие X размерности q . Пусть f  : X → X — биекция. Надстройку M = S ¹ × _f X определяют как фактор [0,1] × X по отношению эквивалентности (1, x ) ~ (0, f ( x )).

M = S ¹ × _f X = [0,1] × X

Тогда M автоматически несет в себе два слоения: ₂ , состоящее из множеств вида F _{2, t} = {( t , x ) _~  : x ∈ X } и ₁ , состоящее из множеств вида F _{2, x 0} = {( t , x ) : t ∈ [0,1] , x ∈ O _{x 0} }, где орбита O _{x 0} определяется как ${\displaystyle {\mathcal {F}}}$ ${\displaystyle {\mathcal {F}}}$

О _{Икс 0} знак равно {..., ж ^-2 ( Икс ₀ ), Ж ^-1 ( Икс ₀ ), Икс ₀ , Ж ( Икс ₀ ), Ж ² ( Икс ₀ ), ...},

где показатель степени относится к тому, сколько раз функция f составлена ​​сама с собой. Обратите внимание, что O _{x 0} = O _{f ( x 0 )} = O _{f ⁻² ( x 0 )} и т. д., то же самое верно и для F _{1, x 0} . Понимание слоения ₁ эквивалентно пониманию динамики отображения f . Если многообразие X уже расслоено, можно использовать конструкцию для увеличения коразмерности слоения, при условии, что f отображает листья в листья. ${\displaystyle {\mathcal {F}}}$

Слоения Кронекера 2-тора являются слоениями надстройки поворотов R _α  : S ¹ → S ¹ на угол α ∈ [0, 2 π ).

Подвеска тора с двумя отверстиями после резки и переклейки. а) Двухдырочный тор с разрезаемыми сечениями; б) геометрическая фигура после разрезания четырьмя гранями.

Более конкретно, если Σ = Σ ₂ — тор с двумя дырками с C ¹ , C ² ∈ Σ, то две вложенные окружности пусть являются произведением слоения 3-многообразия M = Σ × S ¹ с листами Σ × { y }, y ∈ S ¹ . Обратите внимание, что N _i = C _i × S ¹ — вложенный тор, трансверсальный N _i , i = 1,2. Обозначим через Diff ₊ ( S ¹ ) группу диффеоморфизмов S ¹ , сохраняющих ориентацию, и выберем f ₁ , f ₂ ∈ Diff ₊ ( S ¹ ). Разрежьте M вдоль N ₁ и N ₂ , обозначив и обозначив полученные копии N _i , i = 1,2. В этой точке имеется многообразие M' = Σ' × S1 с четырьмя граничными компонентами. _{Слоение} перешло в слоение, трансверсальное границе ∂ M' , каждый слой которого имеет вид Σ' × { y }, y ∈ S ¹ . ${\displaystyle {\mathcal {F}}}$ ${\displaystyle {\mathcal {F}}}$ ${\displaystyle N_{i}^{+}}$ ${\displaystyle N_{i}^{-}}$ ${\displaystyle \left\{N_{i}^{\pm }\right\}_{i=1,2}.}$ ${\displaystyle {\mathcal {F}}}$ ${\displaystyle {\mathcal {F^{\prime }}}}$

Этот лист пересекает ∂ M' в четырех окружностях. _Если z ∈ Ci , соответствующие точки в обозначаются z ^± и «приклеиваются» к отождествлению ${\displaystyle C_{i}^{\pm }\times \{y\}\subset N_{i}^{\pm }.}$ ${\displaystyle C_{i}^{\pm }}$ ${\displaystyle N_{i}^{-}}$ ${\displaystyle N_{i}^{+}}$

${\displaystyle (z^{-},y)\equiv (z^{+},f_{i}(y)),\quad i=1,2.}$

Поскольку f ₁ и f ₂ являются сохраняющими ориентацию диффеоморфизмами S ¹ , они изотопны единице, и многообразие, полученное этой операцией переклейки, гомеоморфно M . Листья , однако, снова собираются, образуя новое слоение ( f ₁ , f ₂ ) M . Если лист L группы ( f ₁ , f ₂ ) содержит кусок Σ' × { y ₀ }, то ${\displaystyle {\mathcal {F^{\prime }}}}$ ${\displaystyle {\mathcal {F}}}$ ${\displaystyle {\mathcal {F}}}$

${\displaystyle L=\bigcup _{g\in G}\Sigma ^{\prime }\times \{g(y_{0})\},}$

где G ⊂ Diff ₊ ( S ¹ ) — подгруппа, порожденная { f ₁ , f ₂ }. Эти копии Σ' связаны друг с другом посредством отождествлений.

( z ^- , грамм ( y ₀ )) ≡ ( z ⁺ , ж ₁ ( грамм ( y ₀ ))) для каждого z ∈ C ₁ ,

( z ^- , грамм ( y ₀ )) ≡ ( z ⁺ , ж ₂ ( грамм ( y ₀ ))) для каждого z ∈ C ₂ ,

где g пробегает G . Лист полностью определяется G -орбитой точки y ₀ ∈ S ¹ и может быть простым или чрезвычайно сложным. Например, лист будет компактным именно в том случае, если соответствующая G -орбита конечна. В качестве крайнего примера, если G тривиально ( f ₁ = f ₂ = id _{S ¹} ), то ( f ₁ , f ₂ ) = . Если орбита плотна в ^S1 , соответствующий лист плотен в M. Например, если f ₁ и f ₂ являются поворотами на рационально независимые кратные 2π, каждый лист будет плотным. В других примерах некоторый лист L имеет замыкание , которое соответствует каждому фактору { w } × S ¹ в канторовом множестве . Аналогичные конструкции можно провести на Σ × I , где I — компактный невырожденный интервал. Здесь берутся f ₁ , f ₂ ∈ Diff ₊ ( I ) и, поскольку ∂ I фиксировано поточечно всеми диффеоморфизмами, сохраняющими ориентацию, получается слоение, имеющее две компоненты ∂ M в качестве листьев. При формировании М' в этом случае получается расслоенное многообразие с углами. В любом случае эта конструкция называется надстройкой пары диффеоморфизмов и является благодатным источником интересных примеров слоений коразмерности один. ${\displaystyle {\mathcal {F}}}$ ${\displaystyle {\mathcal {F}}}$ ${\displaystyle {\bar {L}}}$

Слоения и интегрируемость

Существует тесная связь, если предположить, что все гладко , с векторными полями : если векторное поле X на M никогда не равно нулю, его интегральные кривые дадут одномерное слоение. (т.е. слоение коразмерности n - 1 ).

Это наблюдение обобщается до теоремы Фробениуса , утверждающей, что необходимые и достаточные условия для того, чтобы распределение (т. е. n - p- мерное подрасслоение касательного расслоения многообразия ) касалось слоев слоения, состоит в том, что набор векторов поля, касающиеся распределения, замкнуты скобками Ли . Можно сформулировать это и иначе, как вопрос о приведении структурной группы касательного расслоения из GL( n ) к приводимой подгруппе.

Условия теоремы Фробениуса выступают как условия интегрируемости ; и утверждается, что если они выполняются, то редукция может иметь место, поскольку существуют локальные функции перехода с требуемой блочной структурой. Например, в случае коразмерности 1 мы можем определить касательное расслоение слоения как ker( α ) для некоторого (неканонического) α ∈ Ω ¹ (т.е. ненулевого ковекторного поля). Данное α интегрируемо тогда и только тогда, когда α ∧ dα = 0 всюду.

Существует глобальная теория слоений, поскольку существуют топологические ограничения. Например, в поверхностном случае всюду ненулевое векторное поле может существовать на ориентируемой компактной поверхности только для тора . Это следствие теоремы об индексе Пуанкаре-Хопфа , которая показывает, что эйлерова характеристика должна быть равна 0. Существует множество глубоких связей с контактной топологией , которая является «противоположной» концепцией, требующей, чтобы условие интегрируемости никогда не выполнялось.

Существование слоений

Хефлигер (1970) дал необходимое и достаточное условие того, чтобы распределение на связном некомпактном многообразии было гомотопным интегрируемому распределению. Терстон (1974, 1976) показал, что любое компактное многообразие с распределением имеет слоение той же размерности.

Смотрите также

• G-структура  - Подпучок группы структур на связке касательных кадров.Pages displaying short descriptions of redirect targets
• Структура Хефлигера  – обобщение слоения, замкнутого при откатах.
• Ламинирование  - разделенное топологическое пространство.
• Слоение Риба  – особое слоение трехмерной сферы, введенное французским математиком Жоржем Рибом Pages displaying wikidata descriptions as a fallback.
• Тугое слоение

Примечания

1. Кандел и Конлон 2000, стр. 5
2. Аносов 2001.
3. Гургульон 2012, с. 56
4. Риб, Г. (1959). «Замечания о структурах фейлетеев» (PDF) . Бык. Соц. Математика. Франция . 87 : 445–450. дои : 10.24033/bsmf.1539 . Збл  0122.41603.
5. Лоусон 1974
6. Кандел и Конлон 2000, стр. 19
7. Candel & Conlon 2000, стр. 20
8. Кандел и Конлон 2000, стр. 23
9. Candel & Conlon 2000, стр. 25
10. Candel & Conlon 2000, стр. 26
11. Candel & Conlon 2000, стр. 27
12. Кандел и Конлон 2000, стр. 28
13. Candel & Conlon 2000, стр. 29
14. Candel & Conlon 2000, стр. 31
15. Кандел и Конлон 2000, стр. 32
16. Дерфи, AH (1972). «Слоения нечетных сфер». Анналы математики . Вторая серия. 96 (2): 407–411. дои : 10.2307/1970795. JSTOR  1970795.

Рекомендации

• Аносов, Д.В. (2001) [1994], «Слоение», Математическая энциклопедия , EMS Press
• Кандел, Альберто; Конлон, Лоуренс (2000). Слоения I. Аспирантура по математике. Том. 23. Провиденс, Род-Айленд: Американское математическое общество . ISBN 0-8218-0809-5.
• Кандел, Альберто; Конлон, Лоуренс (2003). Слоения II . Аспирантура по математике. Том. 60. Провиденс, Род-Айленд: Американское математическое общество . ISBN 0-8218-0809-5.
• Гургулон, Эрик (2012). Формализм 3+1 в общей теории относительности. Конспект лекций по физике. Том. 846. Гейдельберг, Нью-Йорк, Дордрехт, Лондон: Springer . дои : 10.1007/978-3-642-24525-1. ISBN 978-3-642-24524-4.
• Хефлигер, Андре (1970), «Feuilletages sur les variétés ouvertes», Топология , 9 (2): 183–194, doi : 10.1016/0040-9383(70)90040-6, ISSN  0040-9383, MR  0263104
• Лоусон, Х. Блейн (1974), «Слоения», Бюллетень Американского математического общества , 80 (3): 369–418, doi : 10.1090/S0002-9904-1974-13432-4 , ISSN  0002-9904, MR  0343289
• Мурдейк, Ике ; Мрчун, Дж. (2003), Введение в слоения и группоиды Ли , Кембриджские исследования по высшей математике, том. 91, Издательство Кембриджского университета , ISBN 978-0-521-83197-0, МР  2012261
• Риб, Жорж (1952), Sur somees proprietés topologiques des variétés feuilletées , Actualités Sci. Индиана, нет. 1183, Hermann & Cie., Париж, MR  0055692
• Терстон, Уильям (1974), «Теория слоений коразмерности больше единицы», Commentarii Mathematici Helvetici , 49 : 214–231, doi : 10.1007/BF02566730, ISSN  0010-2571, MR  0370619, S2CID  120603728
• Терстон, Уильям П. (1976), «Существование слоений коразмерности один», Annals of Mathematics , Second Series, 104 (2): 249–268, doi : 10.2307/1971047, ISSN  0003-486X, JSTOR  1971047, MR  0425985

Внешние ссылки

• Слоения в Атласе многообразий