
Генная (или генетическая ) регуляторная сеть ( GRN ) представляет собой совокупность молекулярных регуляторов, которые взаимодействуют друг с другом и с другими веществами в клетке, чтобы управлять уровнями экспрессии генов мРНК и белков, которые, в свою очередь, определяют функцию клетки. GRN также играют центральную роль в морфогенезе , создании структур тела, что, в свою очередь, является центральным в эволюционной биологии развития (evo-devo).
Регулятором может быть ДНК , РНК , белок или любая комбинация двух или более из этих трех, которые образуют комплекс, например, конкретная последовательность ДНК и фактор транскрипции для активации этой последовательности. Взаимодействие может быть прямым или косвенным (через транскрибированную РНК или транслируемый белок). В общем, каждая молекула мРНК продолжает производить определенный белок (или набор белков). В некоторых случаях этот белок будет структурным и будет накапливаться на клеточной мембране или внутри клетки, придавая ей определенные структурные свойства. В других случаях белок будет ферментом , т. е. микромашиной, которая катализирует определенную реакцию, например, расщепление источника пищи или токсина. Однако некоторые белки служат только для активации других генов, и это факторы транскрипции , которые являются основными игроками в регуляторных сетях или каскадах. Связываясь с промоторной областью в начале других генов, они включают их, инициируя производство другого белка и так далее. Некоторые факторы транскрипции являются ингибирующими. [1]
В одноклеточных организмах регуляторные сети реагируют на внешнюю среду, оптимизируя клетку в определенное время для выживания в этой среде. Таким образом, дрожжевая клетка, оказавшись в растворе сахара, включит гены для выработки ферментов, которые перерабатывают сахар в спирт. [2] Этот процесс, который мы связываем с виноделием, является способом, которым дрожжевая клетка обеспечивает себе жизнь, получая энергию для размножения, что в нормальных условиях повысило бы ее шансы на выживание.
У многоклеточных животных тот же принцип был поставлен на службу каскадам генов, которые контролируют форму тела. [3] Каждый раз, когда клетка делится, в результате получаются две клетки, которые, хотя и содержат один и тот же геном в полном объеме, могут отличаться тем, какие гены включены и производят белки. Иногда «самоподдерживающаяся петля обратной связи» гарантирует, что клетка сохраняет свою идентичность и передает ее дальше. Менее понятен механизм эпигенетики , с помощью которого модификация хроматина может обеспечивать клеточную память, блокируя или позволяя транскрипцию. Основной особенностью многоклеточных животных является использование градиентов морфогенов , которые, по сути, обеспечивают систему позиционирования, которая сообщает клетке, где в организме она находится, и, следовательно, каким типом клетки стать. Ген, включенный в одной клетке, может производить продукт, который покидает клетку и диффундирует через соседние клетки, входя в них и включая гены только тогда, когда он присутствует выше определенного порогового уровня. Таким образом, эти клетки индуцируются в новую судьбу и могут даже генерировать другие морфогены , которые подают сигнал исходной клетке. На более длинных расстояниях морфогены могут использовать активный процесс передачи сигнала . Такая передача сигнала контролирует эмбриогенез , построение плана тела с нуля через ряд последовательных шагов. Они также контролируют и поддерживают взрослые тела через процессы обратной связи , и потеря такой обратной связи из-за мутации может быть ответственна за пролиферацию клеток, которая наблюдается при раке . Параллельно с этим процессом построения структуры каскад генов включает гены, которые производят структурные белки , которые придают каждой клетке необходимые ей физические свойства.
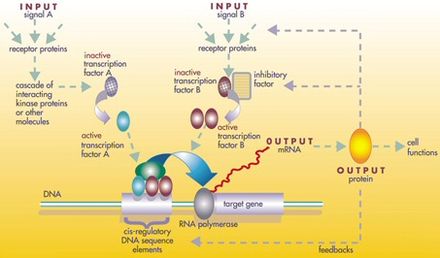
На одном уровне биологические клетки можно рассматривать как «частично смешанные мешки» биологических химикатов — при обсуждении сетей регуляции генов эти химикаты в основном представляют собой матричные РНК (мРНК) и белки , которые возникают в результате экспрессии генов. Эти мРНК и белки взаимодействуют друг с другом с различной степенью специфичности. Некоторые из них диффундируют вокруг клетки. Другие связаны с клеточными мембранами , взаимодействуя с молекулами в окружающей среде. Третьи проходят через клеточные мембраны и передают сигналы дальнего действия другим клеткам в многоклеточном организме. Эти молекулы и их взаимодействия составляют сеть регуляции генов . Типичная сеть регуляции генов выглядит примерно так:
Узлы этой сети могут представлять гены, белки, мРНК, комплексы белок/белок или клеточные процессы. Узлы, изображенные как лежащие вдоль вертикальных линий, связаны с интерфейсами клетка/окружающая среда, в то время как другие являются свободно плавающими и могут диффундировать . Ребра между узлами представляют взаимодействия между узлами, которые могут соответствовать отдельным молекулярным реакциям между ДНК, мРНК, микроРНК, белками или молекулярными процессами, посредством которых продукты одного гена влияют на продукты другого, хотя отсутствие экспериментально полученной информации часто подразумевает, что некоторые реакции не моделируются на таком тонком уровне детализации. Эти взаимодействия могут быть индуктивными (обычно представленными наконечниками стрелок или знаком +), при этом увеличение концентрации одного приводит к увеличению другого, ингибирующими (представленными заполненными кругами, тупыми стрелками или знаком минус), при этом увеличение одного приводит к уменьшению другого, или двойственными, когда в зависимости от обстоятельств регулятор может активировать или ингибировать целевой узел. Узлы могут регулировать себя напрямую или косвенно, создавая петли обратной связи, которые формируют циклические цепи зависимостей в топологической сети. Структура сети является абстракцией молекулярной или химической динамики системы, описывающей многообразные способы, которыми одно вещество влияет на все остальные, с которыми оно связано. На практике такие GRN выводятся из биологической литературы по данной системе и представляют собой выжимку коллективного знания о наборе связанных биохимических реакций. Чтобы ускорить ручное курирование GRN, некоторые недавние попытки пытаются использовать интеллектуальный анализ текста , курируемые базы данных, сетевой вывод из массивных данных, проверку моделей и другие технологии извлечения информации для этой цели. [4]
Гены можно рассматривать как узлы в сети, где входными данными являются белки, такие как факторы транскрипции , а выходными — уровень экспрессии гена . Значение узла зависит от функции, которая зависит от значения его регуляторов на предыдущих временных шагах (в булевой сети, описанной ниже, это булевы функции , как правило, И, ИЛИ и НЕ). Эти функции интерпретируются как выполнение своего рода обработки информации внутри клетки, которая определяет клеточное поведение. Основными драйверами внутри клеток являются концентрации некоторых белков, которые определяют как пространственные (расположение внутри клетки или ткани), так и временные (клеточный цикл или стадия развития) координаты клетки, как своего рода «клеточная память». Генные сети только начинают пониматься, и следующим шагом для биологии является попытка вывести функции для каждого «узла» гена, чтобы помочь понять поведение системы на возрастающих уровнях сложности, от гена до сигнального пути, уровня клетки или ткани. [5]
Математические модели GRN были разработаны для того, чтобы охватить поведение моделируемой системы, и в некоторых случаях генерировать прогнозы, соответствующие экспериментальным наблюдениям. В некоторых других случаях модели доказали свою способность делать точные новые прогнозы, которые можно проверить экспериментально, тем самым предлагая новые подходы для исследования в эксперименте, которые иногда не рассматривались бы при разработке протокола экспериментальной лаборатории. Методы моделирования включают дифференциальные уравнения (ODE), булевы сети, сети Петри , байесовские сети , графические модели гауссовых сетей , стохастические и процессные исчисления . [6] Наоборот, были предложены методы для создания моделей GRN, которые наилучшим образом объясняют набор наблюдений временных рядов . Недавно было показано, что сигнал ChIP-seq модификации гистонов больше коррелирует с мотивами факторов транскрипции на промоторах по сравнению с уровнем РНК. [7] Поэтому предполагается, что временная модификация гистонов ChIP-seq может обеспечить более надежные выводы о сетях регуляции генов по сравнению с методами, основанными на уровнях экспрессии.
Обычно считается, что сети регуляции генов состоят из нескольких высокосвязанных узлов ( концентраторов ) и множества плохо связанных узлов, вложенных в иерархический режим регуляции. Таким образом, сети регуляции генов приближаются к топологии иерархической сети без масштабирования . [8] Это согласуется с точкой зрения, что большинство генов имеют ограниченную плейотропию и работают в регуляторных модулях . [9] Считается, что эта структура развивается из-за предпочтительного прикрепления дублированных генов к более высокосвязанным генам. [8] Недавние исследования также показали, что естественный отбор имеет тенденцию благоприятствовать сетям с редкой связностью. [10]
В основном существуют два способа, которыми могут развиваться сети, оба из которых могут происходить одновременно. Первый заключается в том, что топология сети может быть изменена путем добавления или вычитания узлов (генов) или частей сети (модулей) может быть выражена в разных контекстах. Сигнальный путь Hippo Drosophila является хорошим примером. Сигнальный путь Hippo контролирует как митотический рост, так и постмитотическую клеточную дифференциацию. [11] Недавно было обнаружено, что сеть, в которой работает сигнальный путь Hippo, отличается между этими двумя функциями, что, в свою очередь, изменяет поведение сигнального пути Hippo. Это говорит о том, что сигнальный путь Hippo работает как консервативный регуляторный модуль, который может использоваться для множества функций в зависимости от контекста. [11] Таким образом, изменение топологии сети может позволить консервативному модулю выполнять множество функций и изменять конечный результат сети. Второй способ, которым могут развиваться сети, заключается в изменении силы взаимодействий между узлами, например, того, насколько сильно фактор транскрипции может связываться с цис-регуляторным элементом . Было показано, что такие различия в прочности краев сети лежат в основе межвидовых различий в формировании судьбы клеток вульвы у червей Caenorhabditis . [12]
Другой широко цитируемой характеристикой генной регуляторной сети является обилие определенных повторяющихся подсетей, известных как сетевые мотивы . Сетевые мотивы можно рассматривать как повторяющиеся топологические шаблоны при разделении большой сети на маленькие блоки. Предыдущий анализ обнаружил несколько типов мотивов, которые чаще появлялись в генных регуляторных сетях, чем в случайно сгенерированных сетях. [13] [14] [15] В качестве примера, один из таких мотивов называется петлями прямой связи, которые состоят из трех узлов. Этот мотив является наиболее распространенным среди всех возможных мотивов, состоящих из трех узлов, как показано в генных регуляторных сетях мухи, нематоды и человека. [15]
Было предложено, чтобы обогащенные мотивы следовали конвергентной эволюции , предполагая, что они являются «оптимальными конструкциями» для определенных регуляторных целей. [16] Например, моделирование показывает, что петли прямой связи способны координировать изменение в узле A (с точки зрения концентрации и активности) и динамику экспрессии узла C, создавая различные входные-выходные поведения. [17] [18] Система утилизации галактозы E. coli содержит петлю прямой связи, которая ускоряет активацию оперона утилизации галактозы galETK , потенциально облегчая метаболический переход к галактозе при истощении глюкозы. [19] Петля прямой связи в системах утилизации арабинозы E. coli задерживает активацию оперона катаболизма арабинозы и транспортеров, потенциально избегая ненужного метаболического перехода из-за временных колебаний в восходящих сигнальных путях. [20] Аналогично в сигнальном пути Wnt у Xenopus петля прямой связи действует как детектор изменения кратности, который реагирует на изменение кратности, а не на абсолютное изменение уровня β-катенина, потенциально увеличивая устойчивость к колебаниям уровней β-катенина. [21] Согласно гипотезе конвергентной эволюции, обогащение петель прямой связи было бы адаптацией для быстрого реагирования и устойчивости к шуму. Недавнее исследование показало, что дрожжи, выращенные в среде с постоянной глюкозой, развили мутации в сигнальных путях глюкозы и пути регуляции роста, что предполагает, что регуляторные компоненты, реагирующие на изменения окружающей среды, не являются необходимыми в постоянной среде. [22]
С другой стороны, некоторые исследователи выдвигают гипотезу, что обогащение сетевых мотивов неадаптивно. [23] Другими словами, сети регуляции генов могут эволюционировать к похожей структуре без специфического отбора по предлагаемому поведению ввода-вывода. Поддержка этой гипотезы часто исходит из вычислительного моделирования. Например, колебания в обилии петель прямой связи в модели, которая имитирует эволюцию сетей регуляции генов путем случайной перестройки узлов, могут указывать на то, что обогащение петель прямой связи является побочным эффектом эволюции. [24] В другой модели эволюции сетей регуляции генов соотношение частот дупликации генов и делеции генов оказывает большое влияние на топологию сети: определенные соотношения приводят к обогащению петель прямой связи и создают сети, которые демонстрируют черты иерархических сетей без масштабирования. Эволюция de novo когерентных петель прямой связи типа 1 была продемонстрирована вычислительно в ответ на отбор для их гипотетической функции фильтрации короткого ложного сигнала, поддерживая адаптивную эволюцию, но для неидеализированного шума вместо этого была выбрана динамическая система прямой связи с другой топологией. [25]
Регуляторные сети позволяют бактериям адаптироваться практически к любой экологической нише на Земле. [26] [27] Сеть взаимодействий между различными типами молекул, включая ДНК, РНК, белки и метаболиты, используется бактериями для достижения регуляции экспрессии генов. У бактерий основная функция регуляторных сетей заключается в контроле реакции на изменения окружающей среды, например, на состояние питания и экологический стресс. [28] Сложная организация сетей позволяет микроорганизму координировать и интегрировать множественные сигналы окружающей среды. [26]
Одним из примеров стресса является ситуация, когда окружающая среда внезапно становится бедной питательными веществами. Это запускает сложный процесс адаптации у бактерий , таких как E. coli . После этого изменения окружающей среды тысячи генов меняют уровень экспрессии. Однако эти изменения предсказуемы из топологии и логики генной сети [29] , о которой сообщается в RegulonDB . В частности, в среднем сила реакции гена была предсказуема из разницы между количеством активирующих и репрессирующих входных факторов транскрипции этого гена. [29]
Обычно такую сеть моделируют с помощью набора связанных обыкновенных дифференциальных уравнений (ОДУ) или СДУ , описывающих кинетику реакции составных частей. Предположим, что наша регуляторная сеть имеет узлы, и пусть представляют концентрации соответствующих веществ в момент времени . Тогда временную эволюцию системы можно приблизительно описать следующим образом:
где функции выражают зависимость от концентраций других веществ, присутствующих в клетке. Функции в конечном итоге выводятся из основных принципов химической кинетики или простых выражений, полученных из них, например, ферментативной кинетики Михаэлиса-Ментен . Следовательно, функциональные формы обычно выбираются как полиномы низкого порядка или функции Хилла , которые служат в качестве анзаца для реальной молекулярной динамики. Такие модели затем изучаются с использованием математики нелинейной динамики . Специфическая для системы информация, такая как константы скорости реакции и чувствительности, кодируется как постоянные параметры. [30]
Решая для неподвижной точки системы:
для всех можно получить (возможно, несколько) профилей концентрации белков и мРНК, которые теоретически устойчивы (хотя и не обязательно стабильны ). Таким образом, устойчивые состояния кинетических уравнений соответствуют потенциальным типам клеток, а колебательные решения приведенного выше уравнения — естественно циклическим типам клеток. Математическая устойчивость этих аттракторов обычно может быть охарактеризована знаком высших производных в критических точках, а затем соответствовать биохимической устойчивости профиля концентрации. Критические точки и бифуркации в уравнениях соответствуют критическим состояниям клеток, в которых небольшие возмущения состояния или параметров могут переключать систему между одной из нескольких устойчивых судеб дифференциации. Траектории соответствуют развертыванию биологических путей и переходным процессам уравнений в краткосрочные биологические события. Для более подробного математического обсуждения см. статьи о нелинейности , динамических системах , теории бифуркаций и теории хаоса .
Следующий пример иллюстрирует, как булева сеть может моделировать GRN вместе с ее генными продуктами (выходы) и веществами из окружающей среды, которые на нее влияют (входы). Стюарт Кауффман был среди первых биологов, использовавших метафору булевых сетей для моделирования генетических регуляторных сетей. [31] [32]
Достоверность модели можно проверить, сравнив результаты моделирования с наблюдениями временных рядов. Частичная проверка модели булевой сети может также быть получена путем проверки предсказанного существования еще неизвестной регуляторной связи между двумя конкретными факторами транскрипции, каждый из которых является узлом модели. [33]
Непрерывные сетевые модели GRN являются расширением булевых сетей, описанных выше. Узлы по-прежнему представляют гены, а связи между ними оказывают регуляторное влияние на экспрессию генов. Гены в биологических системах демонстрируют непрерывный диапазон уровней активности, и утверждается, что использование непрерывного представления охватывает несколько свойств сетей регуляции генов, отсутствующих в булевой модели. [34] Формально большинство этих подходов похожи на искусственную нейронную сеть , поскольку входы в узел суммируются, и результат служит входом в сигмоидальную функцию , например, [35], но белки часто контролируют экспрессию генов синергическим, т. е. нелинейным образом. [36] Однако теперь существует непрерывная сетевая модель [37] , которая позволяет группировать входы в узел, тем самым реализуя другой уровень регуляции. Эта модель формально ближе к рекуррентной нейронной сети более высокого порядка . Та же модель также использовалась для имитации эволюции клеточной дифференциации [38] и даже многоклеточного морфогенеза . [39]
Экспериментальные результаты [40] [41] продемонстрировали, что экспрессия генов является стохастическим процессом. Таким образом, многие авторы теперь используют стохастический формализм после работы Аркина и др. [42] Работы по экспрессии отдельных генов [43] и небольшим синтетическим генетическим сетям, [44] [45], таким как генетический тумблер Тима Гарднера и Джима Коллинза , предоставили дополнительные экспериментальные данные о фенотипической изменчивости и стохастической природе экспрессии генов. Первые версии стохастических моделей экспрессии генов включали только мгновенные реакции и управлялись алгоритмом Джиллеспи . [46]
Поскольку некоторые процессы, такие как транскрипция генов, включают множество реакций и не могут быть правильно смоделированы как мгновенная реакция в один шаг, было предложено моделировать эти реакции как одношаговые множественные отложенные реакции, чтобы учесть время, необходимое для завершения всего процесса. [47]
Отсюда был предложен набор реакций [48] , которые позволяют генерировать GRN. Затем они моделируются с использованием модифицированной версии алгоритма Джиллеспи, который может моделировать множественные реакции с задержкой по времени (химические реакции, где каждому из продуктов предоставляется задержка по времени, которая определяет, когда он будет выпущен в систему как «готовый продукт»).
Например, базовую транскрипцию гена можно представить следующей одностадийной реакцией (РНКП — РНК-полимераза, RBS — сайт связывания РНК-рибосомы, а Pro i — промоторная область гена i ):
Более того, похоже, что существует компромисс между шумом в экспрессии генов, скоростью, с которой гены могут переключаться, и метаболическими затратами, связанными с их функционированием. Более конкретно, для любого заданного уровня метаболических затрат существует оптимальный компромисс между шумом и скоростью обработки, а увеличение метаболических затрат приводит к лучшим компромиссам между скоростью и шумом. [49] [50] [51]
В недавней работе был предложен симулятор (SGNSim, Stochastic Gene Networks Simulator ), [52], который может моделировать GRN, где транскрипция и трансляция моделируются как множественные отложенные по времени события, а его динамика управляется алгоритмом стохастического моделирования (SSA), способным иметь дело с множественными отложенными по времени событиями. Временные задержки могут быть получены из нескольких распределений, а скорости реакции — из сложных функций или из физических параметров. SGNSim может генерировать ансамбли GRN в пределах набора определяемых пользователем параметров, таких как топология. Его также можно использовать для моделирования определенных GRN и систем химических реакций. Генетические возмущения, такие как делеции генов, сверхэкспрессия генов, вставки, мутации со сдвигом рамки, также могут быть смоделированы.
GRN создается из графа с желаемой топологией, накладывая распределения входящей и исходящей степеней. На активность промотора гена влияют другие продукты экспрессии генов, которые действуют как входы, в форме мономеров или объединены в мультимеры и устанавливаются как прямые или косвенные. Затем каждый прямой вход назначается участку оператора, и различным факторам транскрипции может быть разрешено или нет конкурировать за один и тот же участок оператора, в то время как косвенным входам назначается цель. Наконец, каждому гену назначается функция, определяющая реакцию гена на комбинацию факторов транскрипции (состояние промотора). Функции переноса (то есть то, как гены реагируют на комбинацию входов) могут быть назначены каждой комбинации состояний промотора по желанию.
В других недавних работах были разработаны многомасштабные модели сетей регуляции генов, которые фокусируются на приложениях синтетической биологии. Были использованы симуляции, которые моделируют все биомолекулярные взаимодействия в транскрипции, трансляции, регуляции и индукции сетей регуляции генов, направляя проектирование синтетических систем. [53]
Другая работа была сосредоточена на прогнозировании уровней экспрессии генов в сети регуляции генов. Подходы, используемые для моделирования сетей регуляции генов, были ограничены интерпретируемостью и, как следствие, в целом являются упрощенными версиями сети. Например, булевы сети использовались из-за их простоты и способности обрабатывать шумные данные, но терять информацию о данных из-за наличия двоичного представления генов. Кроме того, искусственные нейронные сети не используют скрытый слой, чтобы их можно было интерпретировать, теряя возможность моделировать корреляции более высокого порядка в данных. Используя модель, которая не ограничена интерпретируемостью, можно создать более точную модель. Возможность более точно предсказывать экспрессию генов дает способ исследовать, как препараты влияют на систему генов, а также находить, какие гены взаимосвязаны в процессе. Этому способствовал конкурс DREAM [54] , который поощряет конкурс на лучшие алгоритмы прогнозирования. [55] В некоторых других недавних работах использовались искусственные нейронные сети со скрытым слоем. [56]
Существует три класса рассеянного склероза: рецидивирующе-ремиттирующий (RRMS), первично-прогрессирующий (PPMS) и вторично-прогрессирующий (SPMS). Сеть регуляции генов (GRN) играет важную роль в понимании механизма заболевания в этих трех различных классах рассеянного склероза. [57]