Поперечное сечение (физика)

Вероятность возникновения данного процесса при столкновении частиц

В физике поперечное сечение является мерой вероятности того, что определенный процесс будет иметь место при столкновении двух частиц. Например, поперечное сечение Резерфорда является мерой вероятности того, что альфа-частица будет отклонена на заданный угол во время взаимодействия с атомным ядром . Поперечное сечение обычно обозначается σ ( сигма ) и выражается в единицах площади, более конкретно в барнах . В некотором смысле, его можно рассматривать как размер объекта, который возбуждение должно поразить, чтобы процесс произошел, но, точнее, это параметр стохастического процесса .

Когда две дискретные частицы взаимодействуют в классической физике, их взаимное поперечное сечение — это область , поперечная их относительному движению, в пределах которой они должны встретиться, чтобы рассеяться друг от друга. Если частицы представляют собой твердые неупругие сферы , которые взаимодействуют только при контакте, их поперечное сечение рассеяния связано с их геометрическим размером. Если частицы взаимодействуют посредством некоторой дальнодействующей силы, такой как электромагнетизм или гравитация , их поперечное сечение рассеяния, как правило, больше их геометрического размера.

Когда поперечное сечение указывается как дифференциальный предел функции некоторой переменной конечного состояния, такой как угол частицы или энергия, оно называется дифференциальным сечением (см. подробное обсуждение ниже). Когда поперечное сечение интегрируется по всем углам рассеяния (и, возможно, другим переменным), оно называется полным сечением или интегрированным полным сечением . Например, при рэлеевском рассеянии интенсивность, рассеянная под прямым и обратным углами, больше интенсивности, рассеянной вбок, поэтому прямое дифференциальное сечение рассеяния больше перпендикулярного дифференциального сечения, и, складывая все бесконечно малые поперечные сечения по всему диапазону углов с помощью интегрального исчисления, мы можем найти полное сечение.

Сечения рассеяния могут быть определены в ядерной , атомной и элементарной физике для столкновений ускоренных пучков одного типа частиц с мишенями (как неподвижными, так и движущимися) второго типа частиц. Вероятность возникновения любой данной реакции пропорциональна ее сечению. Таким образом, указание сечения для данной реакции является прокси для утверждения вероятности того, что данный процесс рассеяния произойдет.

Измеренная скорость реакции данного процесса сильно зависит от экспериментальных переменных, таких как плотность материала мишени, интенсивность пучка, эффективность обнаружения прибора или установка угла обнаружения прибора. Однако эти величины можно вынести за скобки, что позволяет измерить базовое двухчастичное столкновительное сечение.

Дифференциальные и полные сечения рассеяния являются одними из важнейших измеряемых величин в ядерной , атомной физике и физике элементарных частиц .

При рассеянии света частицей поперечное сечение определяет количество оптической мощности, рассеиваемой светом заданной облученности (мощность на площадь). Важно отметить, что хотя поперечное сечение имеет те же единицы, что и площадь, поперечное сечение не обязательно может соответствовать фактическому физическому размеру цели, заданному другими формами измерения. Нередко фактическая площадь поперечного сечения рассеивающего объекта может быть намного больше или меньше поперечного сечения относительно некоторого физического процесса. Например, плазмонные наночастицы могут иметь поперечные сечения рассеяния света для определенных частот, которые намного больше их фактических площадей поперечного сечения.

Столкновение частиц газа

Рисунок 1. В газе частиц индивидуального диаметра 2 r сечение σ столкновений связано с плотностью числа частиц n и средней длиной свободного пробега между столкновениями λ .

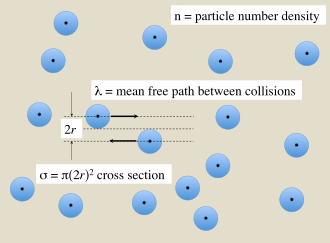
В газе из частиц конечного размера происходят столкновения между частицами, которые зависят от размера их поперечного сечения. Среднее расстояние, которое частица проходит между столкновениями, зависит от плотности частиц газа. Эти величины связаны соотношением

${\displaystyle \sigma ={\frac {1}{n\lambda }},}$

где

σ — поперечное сечение столкновения двух частиц (единица СИ : ^м2 ),

λ — средняя длина свободного пробега между столкновениями (единица СИ: м),

n — плотность числа частиц-мишеней (единица СИ: м ⁻³ ).

Если частицы в газе можно рассматривать как твердые сферы радиуса r, которые взаимодействуют путем прямого контакта, как показано на рисунке 1, то эффективное поперечное сечение столкновения пары равно

${\displaystyle \sigma =\pi \left(2r\right)^{2}}$

Если частицы в газе взаимодействуют посредством силы, радиус действия которой больше их физического размера, то поперечное сечение представляет собой большую эффективную площадь, которая может зависеть от множества переменных, таких как энергия частиц.

Поперечные сечения могут быть вычислены для атомных столкновений, но также используются в субатомной сфере. Например, в ядерной физике «газ» нейтронов низкой энергии сталкивается с ядрами в реакторе или другом ядерном устройстве, с поперечным сечением, которое зависит от энергии и, следовательно, также с четко определенным средним свободным пробегом между столкновениями.

Затухание пучка частиц

Если пучок частиц входит в тонкий слой материала толщиной d z , поток Φ пучка уменьшится на dΦ согласно

${\displaystyle {\frac {\mathrm {d} \Phi }{\mathrm {d} z}}=-n\sigma \Phi ,}$

где σ — полное сечение всех событий, включая рассеяние , поглощение или преобразование в другой вид. Объемная плотность числа рассеивающих центров обозначается n . Решение этого уравнения демонстрирует экспоненциальное затухание интенсивности пучка:

${\displaystyle \Phi =\Phi _{0}e^{-n\sigma z},}$

где Φ ₀ — начальный поток, а z — общая толщина материала. Для света это называется законом Бера-Ламберта .

Дифференциальное сечение

Рассмотрим классическое измерение, в котором одна частица рассеивается от одной неподвижной целевой частицы. Традиционно используется сферическая система координат , при этом цель помещается в начало координат, а ось z этой системы координат совпадает с падающим лучом. Угол θ — это угол рассеяния , измеренный между падающим лучом и рассеянным лучом, а φ — это азимутальный угол .

Параметр удара b представляет собой перпендикулярное смещение траектории входящей частицы, а выходящая частица вылетает под углом θ . Для заданного взаимодействия ( кулоновского , магнитного , гравитационного , контактного и т. д.) параметр удара и угол рассеяния имеют определенную функциональную зависимость один к одному. Обычно параметр удара не может ни контролироваться, ни измеряться от события к событию и предполагается, что он принимает все возможные значения при усреднении по многим событиям рассеяния. Дифференциальный размер поперечного сечения представляет собой элемент площади в плоскости параметра удара, т. е. d σ = b d φ d b . Дифференциальный угловой диапазон рассеянной частицы под углом θ представляет собой элемент телесного угла dΩ = sin θ d θ d φ . Дифференциальное поперечное сечение представляет собой частное этих величин, ⁠д σ/дОм⁠ .

Это функция угла рассеяния (и, следовательно, также параметра удара), а также других наблюдаемых величин, таких как импульс входящей частицы. Дифференциальное сечение всегда принимается положительным, хотя большие параметры удара обычно приводят к меньшему отклонению. В цилиндрически симметричных ситуациях (относительно оси пучка) азимутальный угол φ не изменяется процессом рассеяния, и дифференциальное сечение можно записать как

${\displaystyle {\frac {\mathrm {d} \sigma }{\mathrm {d} (\cos \theta )}}=\int _{0}^{2\pi }{\frac {\mathrm {d} \sigma }{\mathrm {d} \Omega }}\,\mathrm {d} \varphi }$.

В ситуациях, когда процесс рассеяния не является азимутально симметричным, например, когда частицы пучка или мишени обладают магнитными моментами, ориентированными перпендикулярно оси пучка, дифференциальное сечение также должно быть выражено как функция азимутального угла.

При рассеянии частиц падающего потока F _inc на неподвижной мишени, состоящей из многих частиц, дифференциальное сечение ⁠д σ/дОм⁠ под углом ( θ , φ ) связана с потоком рассеянных частиц F _out ( θ , φ ) в частицах в единицу времени соотношением

${\displaystyle {\frac {\mathrm {d} \sigma }{\mathrm {d} \Omega }}(\theta ,\varphi )={\frac {1}{nt\Delta \Omega }}{\frac {F_{\text{out}}(\theta ,\varphi )}{F_{\text{inc}}}}.}$

Здесь ΔΩ — конечный угловой размер детектора (единица СИ: ср ), n — плотность числа целевых частиц (единица СИ: м ⁻³ ), а t — толщина неподвижной мишени (единица СИ: м). Эта формула предполагает, что мишень достаточно тонкая, чтобы каждая частица пучка взаимодействовала не более чем с одной целевой частицей.

Полное поперечное сечение σ может быть восстановлено путем интегрирования дифференциального поперечного сечения ⁠д σ/дОм⁠ по полному телесному углу ( 4π стерадиан):

${\displaystyle \sigma =\oint _{4\pi }{\frac {\mathrm {d} \sigma }{\mathrm {d} \Omega }}\,\mathrm {d} \Omega =\int _{0}^{2\pi }\int _{0}^{\pi }{\frac {\mathrm {d} \sigma }{\mathrm {d} \Omega }}\sin \theta \,\mathrm {d} \theta \,\mathrm {d} \varphi .}$

Обычно опускают квалификатор «дифференциальный» , когда тип поперечного сечения можно вывести из контекста. В этом случае σ можно назвать интегральным сечением или полным сечением . Последний термин может сбивать с толку в контекстах, где задействовано несколько событий, поскольку «полное» может также относиться к сумме поперечных сечений по всем событиям.

Дифференциальное сечение является чрезвычайно полезной величиной во многих областях физики, поскольку его измерение может раскрыть большой объем информации о внутренней структуре частиц-мишеней. Например, дифференциальное сечение рассеяния Резерфорда предоставило убедительные доказательства существования атомного ядра.

Вместо телесного угла в качестве независимой переменной дифференциальных сечений может использоваться переданный импульс .

Дифференциальные сечения неупругого рассеяния содержат резонансные пики , которые указывают на создание метастабильных состояний и содержат информацию об их энергии и времени жизни.

Квантовое рассеяние

В независимом от времени формализме квантового рассеяния начальная волновая функция (до рассеяния) принимается равной плоской волне с определенным импульсом k :

${\displaystyle \phi _{-}(\mathbf {r} )\;{\stackrel {r\to \infty }{\longrightarrow }}\;e^{ikz},}$

где z и r — относительные координаты между снарядом и целью. Стрелка указывает, что это описывает только асимптотическое поведение волновой функции, когда снаряд и цель находятся слишком далеко друг от друга, чтобы взаимодействие имело какой-либо эффект.

После того, как произойдет рассеяние, ожидается, что волновая функция примет следующую асимптотическую форму:

${\displaystyle \phi _{+}(\mathbf {r} )\;{\stackrel {r\to \infty }{\longrightarrow }}\;f(\theta ,\phi ){\frac {e^{ikr}}{r}},}$

где f — некоторая функция угловых координат, известная как амплитуда рассеяния . Эта общая форма верна для любого короткодействующего, сохраняющего энергию взаимодействия. Она неверна для дальнодействующих взаимодействий, поэтому при работе с электромагнитными взаимодействиями возникают дополнительные сложности.

Полная волновая функция системы ведет себя асимптотически как сумма

${\displaystyle \phi (\mathbf {r} )\;{\stackrel {r\to \infty }{\longrightarrow }}\;\phi _{-}(\mathbf {r} )+\phi _{+}(\mathbf {r} ).}$

Дифференциальное сечение связано с амплитудой рассеяния:

${\displaystyle {\frac {\mathrm {d} \sigma }{\mathrm {d} \Omega }}(\theta ,\phi )={\bigl |}f(\theta ,\phi ){\bigr |}^{2}.}$

Это можно просто интерпретировать как плотность вероятности обнаружения рассеянного снаряда под заданным углом.

Поперечное сечение, таким образом, является мерой эффективной площади поверхности, видимой падающими частицами, и как таковое выражается в единицах площади. Поперечное сечение двух частиц (т.е. наблюдаемое, когда две частицы сталкиваются друг с другом) является мерой события взаимодействия между двумя частицами. Поперечное сечение пропорционально вероятности того, что взаимодействие произойдет; например, в простом эксперименте по рассеянию число частиц, рассеянных за единицу времени (ток рассеянных частиц I _r ), зависит только от числа падающих частиц за единицу времени (ток падающих частиц I _i ), характеристик цели (например, числа частиц на единицу поверхности N ) и типа взаимодействия. Для Nσ ≪ 1 мы имеем

${\displaystyle {\begin{aligned}I_{\text{r}}&=I_{\text{i}}N\sigma ,\\\sigma &={\frac {I_{\text{r}}}{I_{\text{i}}}}{\frac {1}{N}}\\&={\text{probability of interaction}}\times {\frac {1}{N}}.\end{aligned}}}$

Связь с S-матрицей

Если приведенные массы и импульсы сталкивающейся системы равны m _i , p _i и m _f , p _f до и после столкновения соответственно, то дифференциальное сечение определяется выражением ^{[ необходимо разъяснение ]}

${\displaystyle {\frac {\mathrm {d} \sigma }{\mathrm {d} \Omega }}=\left(2\pi \right)^{4}m_{\text{i}}m_{\text{f}}{\frac {p_{\text{f}}}{p_{\text{i}}}}{\bigl |}T_{{\text{f}}{\text{i}}}{\bigr |}^{2},}$

где матрица T на оболочке определяется как

${\displaystyle S_{{\text{f}}{\text{i}}}=\delta _{{\text{f}}{\text{i}}}-2\pi i\delta \left(E_{\text{f}}-E_{\text{i}}\right)\delta \left(\mathbf {p} _{\text{i}}-\mathbf {p} _{\text{f}}\right)T_{{\text{f}}{\text{i}}}}$

в терминах S-матрицы . Здесь δ — дельта-функция Дирака . Вычисление S-матрицы является основной целью теории рассеяния .

Единицы

Хотя единицей измерения полного поперечного сечения в системе СИ является м2 , на практике обычно используется меньшая единица.

В ядерной физике и физике элементарных частиц общепринятой единицей является барн б , где 1 б = 10 ⁻²⁸  м ² = 100  фм ² . ^[1] Меньшие префиксные единицы, такие как мб и мкб, также широко используются. Соответственно, дифференциальное сечение может быть измерено в таких единицах, как мб/ср.

Когда рассеянное излучение является видимым светом, принято измерять длину пути в сантиметрах . Чтобы избежать необходимости в коэффициентах пересчета, сечение рассеяния выражается в см2 ^, а числовая концентрация в см ⁻³ . Измерение рассеяния видимого света известно как нефелометрия и эффективно для частиц диаметром 2–50  мкм : как таковое, оно широко используется в метеорологии и при измерении загрязнения атмосферы .

Рассеяние рентгеновских лучей также можно описать с помощью сечений рассеяния, в этом случае квадратный ангстрем является удобной единицей: 1 Å ² = ¹⁰⁻²⁰  м ² =10 000  пм ² = 10 ⁸  б. Сумма сечений рассеяния, фотоэлектрических и парных сечений (в барнах) представлена ​​в виде «атомного коэффициента ослабления» (узкий пучок) в барнах. ^[2]

Рассеивание света

Для света, как и в других условиях, сечение рассеяния частиц обычно отличается от геометрического сечения частицы и зависит от длины волны света и диэлектрической проницаемости , формы и размера частицы. Общее количество рассеяния в разреженной среде пропорционально произведению сечения рассеяния и числа присутствующих частиц.

При взаимодействии света с частицами происходит множество процессов, каждый из которых имеет свое собственное сечение, включая поглощение , рассеяние и фотолюминесценцию . Сумму сечений поглощения и рассеяния иногда называют сечением затухания или экстинкции.

${\displaystyle \sigma =\sigma _{\text{abs}}+\sigma _{\text{sc}}+\sigma _{\text{lum}}.}$

Полное сечение экстинкции связано с ослаблением интенсивности света посредством закона Бера-Ламберта , который гласит, что ослабление пропорционально концентрации частиц:

${\displaystyle A_{\lambda }=Cl\sigma ,}$

где A _λ — затухание на данной длине волны λ , C — концентрация частиц как числовая плотность, а l — длина пути . Поглощение излучения — это логарифм ( десятичный или, чаще, натуральный ) обратной величины пропускания T : ^[3]

${\displaystyle A_{\lambda }=-\log {\mathcal {T}}.}$

Объединение сечений рассеяния и поглощения таким образом часто необходимо из-за невозможности их экспериментального различения, и много исследовательских усилий было вложено в разработку моделей, позволяющих их различить, причем теория Кубелки-Мунка является одной из важнейших в этой области.

Поперечное сечение и теория Ми

Сечения, обычно вычисляемые с помощью теории Ми, включают коэффициенты эффективности для сечений экстинкции , рассеяния и поглощения . Они нормализуются геометрическими сечениями частицы как Поперечное сечение определяется как ${\textstyle Q_{\text{ext}}}$ ${\textstyle Q_{\text{sc}}}$ ${\textstyle Q_{\text{abs}}}$ ${\textstyle \sigma _{\text{geom}}=\pi a^{2}}$ $${\displaystyle Q_{\alpha }={\frac {\sigma _{\alpha }}{\sigma _{\text{geom}}}},\qquad \alpha ={\text{ext}},{\text{sc}},{\text{abs}}.}$$

${\displaystyle \sigma _{\alpha }={\frac {W_{\alpha }}{I_{\text{inc}}}}}$

где - поток энергии через окружающую поверхность, а - интенсивность падающей волны. Для плоской волны интенсивность будет , где - импеданс среды-хозяина . ${\displaystyle \left[W_{\alpha }\right]=\left[{\text{W}}\right]}$ ${\displaystyle \left[I_{\text{inc}}\right]=\left[{\frac {\text{W}}{{\text{m}}^{2}}}\right]}$ ${\displaystyle I_{\text{inc}}=|\mathbf {E} |^{2}/(2\eta )}$ ${\displaystyle \eta ={\sqrt {\mu \mu _{0}/(\varepsilon \varepsilon _{0})}}}$

Основной подход основан на следующем. Во-первых, мы строим воображаемую сферу радиусом (поверхность ) вокруг частицы (рассеивателя). Чистая скорость прохождения электромагнитной энергии через поверхность равна ${\displaystyle r}$ ${\displaystyle A}$ ${\displaystyle A}$

${\displaystyle W_{\text{a}}=-\oint _{A}\mathbf {\Pi } \cdot {\hat {\mathbf {r} }}dA}$

где — усредненный по времени вектор Пойнтинга. Если энергия поглощается внутри сферы, в противном случае энергия создается внутри сферы. Мы не будем рассматривать этот случай здесь. Если принимающая среда не поглощает, энергия должна быть поглощена частицей. Мы разлагаем полное поле на падающую и рассеянную части , и то же самое для магнитного поля . Таким образом, мы можем разложить на три члена , где ${\textstyle \mathbf {\Pi } ={\frac {1}{2}}\operatorname {Re} \left[\mathbf {E} ^{*}\times \mathbf {H} \right]}$ ${\displaystyle W_{\text{a}}>0}$ ${\displaystyle \mathbf {E} =\mathbf {E} _{\text{i}}+\mathbf {E} _{\text{s}}}$ ${\displaystyle \mathbf {H} }$ ${\displaystyle W_{a}}$ ${\displaystyle W_{\text{a}}=W_{\text{i}}-W_{\text{s}}+W_{\text{ext}}}$

${\displaystyle W_{\text{i}}=-\oint _{A}\mathbf {\Pi } _{\text{i}}\cdot {\hat {\mathbf {r} }}dA\equiv 0,\qquad W_{\text{s}}=\oint _{A}\mathbf {\Pi } _{\text{s}}\cdot {\hat {\mathbf {r} }}dA,\qquad W_{\text{ext}}=\oint _{A}\mathbf {\Pi } _{\text{ext}}\cdot {\hat {\mathbf {r} }}dA.}$

где , , и . ${\displaystyle \mathbf {\Pi } _{\text{i}}={\frac {1}{2}}\operatorname {Re} \left[\mathbf {E} _{\text{i}}^{*}\times \mathbf {H} _{\text{i}}\right]}$ ${\displaystyle \mathbf {\Pi } _{\text{s}}={\frac {1}{2}}\operatorname {Re} \left[\mathbf {E} _{\text{s}}^{*}\times \mathbf {H} _{\text{s}}\right]}$ ${\displaystyle \mathbf {\Pi } _{\text{ext}}={\frac {1}{2}}\operatorname {Re} \left[\mathbf {E} _{s}^{*}\times \mathbf {H} _{i}+\mathbf {E} _{i}^{*}\times \mathbf {H} _{s}\right]}$

Все поле можно разложить в ряд векторных сферических гармоник (VSH) . После этого можно взять все интегралы. В случае однородной сферы радиуса , диэлектрической проницаемости и магнитной проницаемости задача имеет точное решение. ^[4] Коэффициенты рассеяния и затухания равны Где . Они связаны как ${\displaystyle a}$ ${\displaystyle \varepsilon }$ ${\displaystyle \mu }$ $${\displaystyle Q_{\text{sc}}={\frac {2}{k^{2}a^{2}}}\sum _{n=1}^{\infty }(2n+1)(|a_{n}|^{2}+|b_{n}|^{2})}$$ $${\displaystyle Q_{\text{ext}}={\frac {2}{k^{2}a^{2}}}\sum _{n=1}^{\infty }(2n+1)\Re (a_{n}+b_{n})}$$ ${\textstyle k=n_{\text{host}}k_{0}}$ $${\displaystyle \sigma _{\text{ext}}=\sigma _{\text{sc}}+\sigma _{\text{abs}}\qquad {\text{or}}\qquad Q_{\text{ext}}=Q_{\text{sc}}+Q_{\text{abs}}}$$

Дипольное приближение для сечения рассеяния

Предположим, что частица поддерживает только электрические и магнитные дипольные моды с поляризуемостями и (здесь мы используем обозначение магнитной поляризуемости в стиле Бекшаева и др. ^{[5] [6],} а не обозначение Ньето-Весперинаса и др. ^[7] ), выраженное через коэффициенты Ми как Тогда поперечные сечения определяются как и, наконец, электрические и магнитные сечения поглощения равны и ${\textstyle \mathbf {p} =\alpha ^{e}\mathbf {E} }$ ${\textstyle \mathbf {m} =(\mu \mu _{0})^{-1}\alpha ^{m}\mathbf {H} }$ $${\displaystyle \alpha ^{e}=4\pi \varepsilon _{0}\cdot i{\frac {3\varepsilon }{2k^{3}}}a_{1},\qquad \alpha ^{m}=4\pi \mu _{0}\cdot i{\frac {3\mu }{2k^{3}}}b_{1}.}$$ $${\displaystyle \sigma _{\text{ext}}=\sigma _{\text{ext}}^{\text{(e)}}+\sigma _{\text{ext}}^{\text{(m)}}={\frac {1}{4\pi \varepsilon \varepsilon _{0}}}\cdot 4\pi k\Im (\alpha ^{e})+{\frac {1}{4\pi \mu \mu _{0}}}\cdot 4\pi k\Im (\alpha ^{m})}$$ $${\displaystyle \sigma _{\text{sc}}=\sigma _{\text{sc}}^{\text{(e)}}+\sigma _{\text{sc}}^{\text{(m)}}={\frac {1}{(4\pi \varepsilon \varepsilon _{0})^{2}}}\cdot {\frac {8\pi }{3}}k^{4}|\alpha ^{e}|^{2}+{\frac {1}{(4\pi \mu \mu _{0})^{2}}}\cdot {\frac {8\pi }{3}}k^{4}|\alpha ^{m}|^{2}}$$ ${\textstyle \sigma _{\text{abs}}=\sigma _{\text{abs}}^{\text{(e)}}+\sigma _{\text{abs}}^{\text{(m)}}}$ $${\displaystyle \sigma _{\text{abs}}^{\text{(e)}}={\frac {1}{4\pi \varepsilon \varepsilon _{0}}}\cdot 4\pi k\left[\Im (\alpha ^{e})-{\frac {k^{3}}{6\pi \varepsilon \varepsilon _{0}}}|\alpha ^{e}|^{2}\right]}$$ $${\displaystyle \sigma _{\text{abs}}^{\text{(m)}}={\frac {1}{4\pi \mu \mu _{0}}}\cdot 4\pi k\left[\Im (\alpha ^{m})-{\frac {k^{3}}{6\pi \mu \mu _{0}}}|\alpha ^{m}|^{2}\right]}$$

Для случая частицы без внутреннего усиления, т.е. частицы не излучающей энергию внутрь ( ), мы имеем частный случай Оптической теоремы. Равенство имеет место для непоглощающих частиц, т.е. для . ${\textstyle \sigma _{\text{abs}}>0}$ $${\displaystyle {\frac {1}{4\pi \varepsilon \varepsilon _{0}}}\Im (\alpha ^{e})+{\frac {1}{4\pi \mu \mu _{0}}}\Im (\alpha ^{m})\geq {\frac {2k^{3}}{3}}\left[{\frac {|\alpha ^{e}|^{2}}{(4\pi \varepsilon \varepsilon _{0})^{2}}}+{\frac {|\alpha ^{m}|^{2}}{(4\pi \mu \mu _{0})^{2}}}\right]}$$ ${\textstyle \Im (\varepsilon )=\Im (\mu )=0}$

Рассеяние света на протяженных телах

В контексте рассеяния света на протяженных телах сечение рассеяния, σ _sc , описывает вероятность того, что свет будет рассеян макроскопической частицей. В общем случае сечение рассеяния отличается от геометрического сечения частицы, поскольку оно зависит от длины волны света и диэлектрической проницаемости в дополнение к форме и размеру частицы. Общая величина рассеяния в разреженной среде определяется произведением сечения рассеяния и числа присутствующих частиц. С точки зрения площади полное сечение ( σ ) представляет собой сумму сечений, обусловленных поглощением , рассеянием и люминесценцией :

${\displaystyle \sigma =\sigma _{\text{abs}}+\sigma _{\text{sc}}+\sigma _{\text{lum}}.}$

Полное поперечное сечение связано с поглощением интенсивности света через закон Бера-Ламберта , который гласит, что поглощение пропорционально концентрации: A _λ = Clσ , где A _λ - поглощение на данной длине волны λ , C - концентрация как числовая плотность , а l - длина пути . Затухание или поглощение излучения - это логарифм ( десятичный или, чаще, натуральный ) обратной величины пропускания T : ^[3]

${\displaystyle A_{\lambda }=-\log {\mathcal {T}}.}$

Отношение к физическому размеру

Не существует простой связи между поперечным сечением рассеяния и физическим размером частиц, поскольку поперечный разрез рассеяния зависит от длины волны используемого излучения. Это можно увидеть, глядя на гало, окружающее Луну, в прилично туманный вечер: фотоны красного света испытывают большую площадь поперечного сечения капель воды, чем фотоны с более высокой энергией. Таким образом, гало вокруг Луны имеет периметр красного света из-за того, что фотоны с более низкой энергией рассеиваются дальше от центра Луны. Фотоны из остальной части видимого спектра остаются в центре гало и воспринимаются как белый свет.

Метеорологический диапазон

Эффективное сечение рассеяния связано с метеорологическим диапазоном L _V :

${\displaystyle L_{\text{V}}={\frac {3.9}{C\sigma _{\text{scat}}}}.}$

Величину Cσ _scat иногда обозначают как b _scat , коэффициент рассеяния на единицу длины. ^[8]

Примеры

Упругое столкновение двух твердых сфер

Следующие уравнения применяются к двум твердым сферам, которые подвергаются абсолютно упругому столкновению. ^[9] Пусть R и r обозначают радиусы рассеивающего центра и рассеиваемой сферы соответственно. Дифференциальное сечение равно

${\displaystyle {\frac {d\sigma }{d\Omega }}={\frac {R^{2}}{4}},}$

и полное поперечное сечение равно

${\displaystyle \sigma _{\text{tot}}=\pi \left(r+R\right)^{2}.}$

Другими словами, полное сечение рассеяния равно площади круга (радиусом r + R ), в который должен попасть центр масс падающей сферы, чтобы она отклонилась.

Рассеяние Резерфорда

При рассеянии Резерфорда падающая частица с зарядом q и энергией E рассеивается на неподвижной частице с зарядом Q. Дифференциальное сечение равно

${\displaystyle {\frac {d\sigma }{d\Omega }}=\left({\frac {q\,Q}{16\pi \varepsilon _{0}E\sin ^{2}(\theta /2)}}\right)^{2}}$

где — диэлектрическая проницаемость вакуума . ^[10] Полное сечение бесконечно, если не применяется ограничение для малых углов рассеяния. ^[11] Это происходит из-за большого диапазона кулоновского потенциала. ${\displaystyle \varepsilon _{0}}$ ${\displaystyle \theta }$ ${\displaystyle 1/r}$

Рассеяние от двумерного круглого зеркала

Следующий пример касается луча света, рассеивающегося от окружности с радиусом r и идеально отражающей границей. Луч состоит из равномерной плотности параллельных лучей, а взаимодействие луча с окружностью моделируется в рамках геометрической оптики . Поскольку задача действительно двумерна, поперечное сечение имеет единицу длины (например, метр). Пусть α будет углом между световым лучом и радиусом, соединяющим точку отражения луча с центральной точкой зеркала. Тогда увеличение элемента длины, перпендикулярного лучу, равно

${\displaystyle \mathrm {d} x=r\cos \alpha \,\mathrm {d} \alpha .}$

Угол отражения этого луча по отношению к входящему лучу равен 2 α , а угол рассеяния равен

${\displaystyle \theta =\pi -2\alpha .}$

Дифференциальное соотношение между падающей и отраженной интенсивностью I равно

${\displaystyle I\,\mathrm {d} \sigma =I\,\mathrm {d} x(x)=Ir\cos \alpha \,\mathrm {d} \alpha =I{\frac {r}{2}}\sin \left({\frac {\theta }{2}}\right)\,\mathrm {d} \theta =I{\frac {\mathrm {d} \sigma }{\mathrm {d} \theta }}\,\mathrm {d} \theta .}$

Дифференциальное сечение, таким образом, равно ( dΩ = d θ )

${\displaystyle {\frac {\mathrm {d} \sigma }{\mathrm {d} \theta }}={\frac {r}{2}}\sin \left({\frac {\theta }{2}}\right).}$

Его максимум при θ = π соответствует обратному рассеянию, а его минимум при θ = 0 соответствует рассеянию от края круга прямо вперед. Это выражение подтверждает интуитивные ожидания, что зеркальный круг действует как рассеивающая линза . Полное поперечное сечение равно диаметру круга:

${\displaystyle \sigma =\int _{0}^{2\pi }{\frac {\mathrm {d} \sigma }{\mathrm {d} \theta }}\,\mathrm {d} \theta =\int _{0}^{2\pi }{\frac {r}{2}}\sin \left({\frac {\theta }{2}}\right)\,\mathrm {d} \theta =2r.}$

Рассеяние от трехмерного сферического зеркала

Результат предыдущего примера можно использовать для решения аналогичной задачи в трех измерениях, т. е. рассеяния от идеально отражающей сферы радиуса a .

Плоскость, перпендикулярная входящему световому лучу, может быть параметризована цилиндрическими координатами r и φ . В любой плоскости входящего и отраженного луча мы можем записать (из предыдущего примера):

${\displaystyle {\begin{aligned}r&=a\sin \alpha ,\\\mathrm {d} r&=a\cos \alpha \,\mathrm {d} \alpha ,\end{aligned}}}$

в то время как элемент зоны воздействия -

${\displaystyle \mathrm {d} \sigma =\mathrm {d} r(r)\times r\,\mathrm {d} \varphi ={\frac {a^{2}}{2}}\sin \left({\frac {\theta }{2}}\right)\cos \left({\frac {\theta }{2}}\right)\,\mathrm {d} \theta \,\mathrm {d} \varphi .}$

В сферических координатах,

${\displaystyle \mathrm {d} \Omega =\sin \theta \,\mathrm {d} \theta \,\mathrm {d} \varphi .}$

Вместе с тригонометрическим тождеством

${\displaystyle \sin \theta =2\sin \left({\frac {\theta }{2}}\right)\cos \left({\frac {\theta }{2}}\right),}$

мы получаем

${\displaystyle {\frac {\mathrm {d} \sigma }{\mathrm {d} \Omega }}={\frac {a^{2}}{4}}.}$

Полное поперечное сечение равно

${\displaystyle \sigma =\oint _{4\pi }{\frac {\mathrm {d} \sigma }{\mathrm {d} \Omega }}\,\mathrm {d} \Omega =\pi a^{2}.}$

Смотрите также

• Поперечное сечение (геометрия)
• Скорость потока
• Светимость (теория рассеяния)
• Линейный коэффициент затухания
• Коэффициент затухания массы
• Сечение нейтрона
• Ядерное сечение
• Сечение гамма-излучения
• Анализ частичной волны
• Детектор частиц
• Радарное поперечное сечение
• Рассеяние Резерфорда
• Амплитуда рассеяния

Ссылки

1. Международное бюро мер и весов (2006), Международная система единиц (СИ) (PDF) (8-е изд.), стр. 127–28, ISBN 92-822-2213-6, заархивировано (PDF) из оригинала 2021-06-04 , извлечено 2021-12-16
2. Справочник по неразрушающему контролю, том 4. Радиографический контроль, ASNT, 2002, глава 22.
3. Bajpai, PK (2008). Биологическое приборостроение и методология (пересмотренное 2-е изд.). Ram Nagar, Нью-Дели: S. Chand & Company Ltd. ISBN 9788121926331. OCLC  943495167.
4. Борен, Крейг Ф. и Дональд Р. Хаффман. Поглощение и рассеяние света малыми частицами. John Wiley & Sons, 2008.
5. Бекшаев, А Я (2013-04-01). "Частицы субволновой длины в неоднородном световом поле: оптические силы, связанные со спиновыми и орбитальными потоками энергии". Журнал оптики . 15 (4): 044004. arXiv : 1210.5730 . Bibcode : 2013JOpt...15d4004B. doi : 10.1088/2040-8978/15/4/044004. ISSN  2040-8978. S2CID  119234614.
6. Блиох, Константин Ю.; Бекшаев, Александр Ю.; Нори, Франко (2014-03-06). "Необыкновенный импульс и спин в затухающих волнах". Nature Communications . 5 (1). Springer Science and Business Media LLC: 3300. arXiv : 1308.0547 . Bibcode :2014NatCo...5.3300B. doi : 10.1038/ncomms4300 . ISSN  2041-1723. PMID  24598730. S2CID  15832637.
7. Nieto-Vesperinas, M.; Sáenz, JJ; Gómez-Medina, R.; Chantada, L. (2010-05-14). "Оптические силы на малых магнитодиэлектрических частицах". Optics Express . 18 (11). The Optical Society: 11428–11443. Bibcode : 2010OExpr..1811428N. doi : 10.1364/oe.18.011428 . ISSN  1094-4087. PMID  20589003.
8. IUPAC , Compendium of Chemical Terminology , 2nd ed. (The "Gold Book") (1997). Онлайн-исправленная версия: (2006–) "Scattering cross section, σscat". doi :10.1351/goldbook.S05490
9. Тейлор 2005, стр. 564, 574.
10. Тейлор 2005, стр. 576.
11. Гриффитс 2005, стр. 409.

Библиография

• Гриффитс, Дэвид Дж. (2005). Введение в квантовую механику . Pearson Prentice Hall. ISBN 0-13-111892-7. OCLC  53926857.
• Тейлор, Джон Р. (2005). Классическая механика . Милл-Вэлли, Калифорния. ISBN 1-891389-22-X. OCLC  55729992.{{cite book}}: CS1 maint: location missing publisher (link)
• Дж. Д. Бьёркен, С. Д. Дрелл, Релятивистская квантовая механика , 1964
• П. Роман, Введение в квантовую теорию , 1969
• В. Грейнер, Дж. Рейнхардт, Квантовая электродинамика , 1994
• РГ Ньютон. Теория рассеяния волн и частиц . McGraw Hill, 1966.
• RC Fernow (1989). Введение в экспериментальную физику элементарных частиц. Cambridge University Press. ISBN 978-0-521-379-403.

Внешние ссылки

• Ядерное поперечное сечение
• Сечение рассеяния
• МАГАТЭ – Службы ядерных данных
• BNL – Национальный центр ядерных данных
• Группа данных по частицам – Обзор физики частиц
• Золотая книга ИЮПАК – Определение: Поперечное сечение реакции
• Золотая книга ИЮПАК – Определение: Поперечное сечение столкновения
• Построитель поперечных сечений ShimPlotWell для ядерных данных