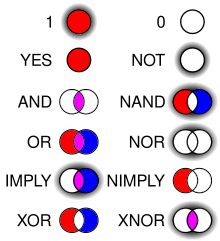
Логика в информатике охватывает область пересечения между логикой и информатикой . Тему можно по существу разделить на три основные области:
Логика играет фундаментальную роль в информатике. Некоторые из ключевых областей логики, которые особенно значимы, — это теория вычислимости (ранее называвшаяся теорией рекурсии), модальная логика и теория категорий . Теория вычислений основана на концепциях, определенных логиками и математиками, такими как Алонзо Чёрч и Алан Тьюринг . [1] [2] Чёрч первым показал существование алгоритмически неразрешимых проблем, используя свое понятие лямбда-определимости. Тьюринг дал первый убедительный анализ того, что можно назвать механической процедурой, и Курт Гёдель утверждал, что он нашел анализ Тьюринга «идеальным». [3] Кроме того, некоторые другие основные области теоретического пересечения между логикой и информатикой:
Одним из первых приложений, использующих термин искусственный интеллект, была система Logic Theorist, разработанная Алленом Ньюэллом , Клиффом Шоу и Гербертом Саймоном в 1956 году. Одна из вещей, которую делает логик, — это берет набор утверждений в логике и выводит заключения (дополнительные утверждения), которые должны быть истинными по законам логики. Например, если даны утверждения «Все люди смертны» и «Сократ — человек», то допустимым заключением будет «Сократ смертен». Конечно, это тривиальный пример. В реальных логических системах утверждения могут быть многочисленными и сложными. Было рано осознано, что этот вид анализа может быть значительно облегчен с помощью использования компьютеров. Logic Theorist подтвердил теоретическую работу Бертрана Рассела и Альфреда Норта Уайтхеда в их влиятельной работе по математической логике под названием Principia Mathematica . Кроме того, последующие системы использовались логиками для проверки и открытия новых математических теорем и доказательств. [7]
Математическая логика всегда оказывала сильное влияние на область искусственного интеллекта (ИИ). С самого начала этой области было осознано, что технология автоматизации логических выводов может иметь большой потенциал для решения проблем и получения выводов из фактов. Рон Брахман описал логику первого порядка (ЛП) как метрику, с помощью которой следует оценивать все формализмы представления знаний ИИ . Логика первого порядка является общим и мощным методом описания и анализа информации. Причина, по которой сам ЛП просто не используется в качестве компьютерного языка, заключается в том, что он на самом деле слишком выразителен , в том смысле, что ЛП может легко выражать утверждения, которые ни один компьютер, каким бы мощным он ни был, никогда не сможет решить. По этой причине каждая форма представления знаний в некотором смысле является компромиссом между выразительностью и вычислимостью . Чем выразительнее язык, тем ближе он к ЛП, тем больше вероятность, что он будет медленнее и склонен к бесконечному циклу. [8]
Например, правила IF–THEN, используемые в экспертных системах, приближаются к очень ограниченному подмножеству FOL. Вместо произвольных формул с полным набором логических операторов отправной точкой является просто то, что логики называют modus ponens . В результате системы на основе правил могут поддерживать высокопроизводительные вычисления, особенно если они используют преимущества алгоритмов оптимизации и компиляции. [9]
С другой стороны, логическое программирование , которое объединяет подмножество предложений Хорна логики первого порядка с немонотонной формой отрицания , имеет как высокую выразительную силу, так и эффективные реализации . В частности, язык логического программирования Prolog является полным по Тьюрингу языком программирования. Datalog расширяет модель реляционной базы данных рекурсивными отношениями, в то время как программирование набора ответов является формой логического программирования, ориентированной на сложные (прежде всего NP-трудные ) задачи поиска .
Другой важной областью исследований логической теории является программная инженерия . Исследовательские проекты, такие как программы Knowledge Based Software Assistant и Programmer's Apprentice, применяли логическую теорию для проверки правильности спецификаций программного обеспечения . Они также использовали логические инструменты для преобразования спецификаций в эффективный код на различных платформах и для доказательства эквивалентности между реализацией и спецификацией. [10] Этот формальный подход, основанный на преобразованиях, часто гораздо более трудоемок, чем традиционная разработка программного обеспечения. Однако в определенных областях с соответствующими формализмами и повторно используемыми шаблонами подход оказался жизнеспособным для коммерческих продуктов. Соответствующими областями обычно являются такие, как системы оружия, системы безопасности и финансовые системы реального времени, где отказ системы имеет чрезмерно высокие человеческие или финансовые издержки. Примером такой области является проектирование сверхбольших интегральных схем (VLSI) — процесс проектирования микросхем, используемых для ЦП и других критических компонентов цифровых устройств. Ошибка в микросхеме может иметь катастрофические последствия. В отличие от программного обеспечения, микросхемы нельзя исправить или обновить. В результате, существует коммерческое обоснование использования формальных методов для доказательства того, что реализация соответствует спецификации. [11]
Другое важное применение логики в компьютерных технологиях было в области языков фреймов и автоматических классификаторов. Языки фреймов, такие как KL-ONE, могут быть напрямую сопоставлены с теорией множеств и логикой первого порядка. Это позволяет специализированным доказателям теорем, называемым классификаторами, анализировать различные декларации между множествами , подмножествами и отношениями в данной модели. Таким образом, модель может быть проверена, а любые несоответствующие определения отмечены. Классификатор также может выводить новую информацию, например, определять новые множества на основе существующей информации и изменять определение существующих множеств на основе новых данных. Уровень гибкости идеален для обработки постоянно меняющегося мира Интернета. Технология классификаторов построена поверх языков, таких как язык веб-онтологии, чтобы обеспечить логический семантический уровень поверх существующего Интернета. Этот уровень называется семантической сетью . [12] [13]
Временная логика используется для рассуждений в параллельных системах . [14]
Хорошая новость в сведении службы KR к доказательству теорем заключается в том, что теперь у нас есть очень четкое, очень конкретное представление о том, что должна делать система KR; плохая новость заключается в том, что также ясно, что услуги не могут быть предоставлены... решение о том, является ли предложение в FOL теоремой... неразрешимо.